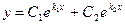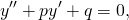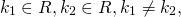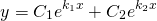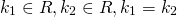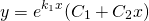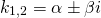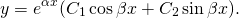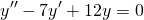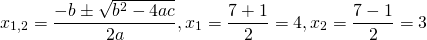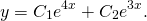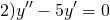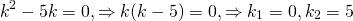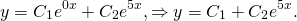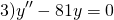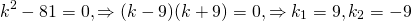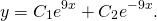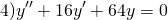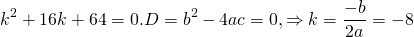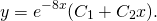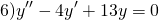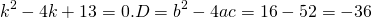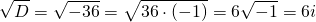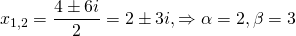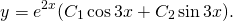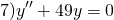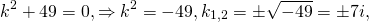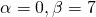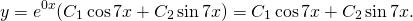Как решать дифференциальные уравнения 2 порядка если дискриминант равен 0

Видео:ЛОДУ 2 порядка c постоянными коэффициентамиСкачать

Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.

Линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами называется уравнение

Для того, чтобы решить это уравнение надо составить характеристическое уравнение, которое получается из данного уравнения , если в нем заменить y»=k 2 , y’=k, a y=k 0 =1.

— это квадратное уравнение.

Общее решение характеристического уравнения строиться в зависимости от характера его корней.

Возможны три случая:

— дискриминант квадратного уравнения больше нуля D > 0 , уравнение имеет два действительный различных корня, k₁≠ k₂, и общее решение характеристического уравнения имеет вид:

— дискриминант характеристического квадратного уравнения равен нулю D= 0, уравнение имеет два действительный кратных корня, k₁= k₂= k, и общее решение уравнения имеет вид:

— дискриминант квадратного уравнения меньше нуля D 2 +7k+6=0.

Решим его: D=49-24=25, k₁= -1, k₂ = -6. Так как корни действительные и разные, то, согласно формулы , получаем общее решение:

Пример 10.9. Найти общее решение дифференциального уравнения

Решение. Составим характеристическое уравнение

Решим это уравнение: D = 36 -36 = 0, k₁ = k₂ =3. Характеристическое уравнение имеет два действительных кратных корня, следовательно, общее решение находим по формуле :

Пример 10.10. Найти общее решение дифференциального уравнения

Решение. Составим характеристическое уравнение

Решим его. Дискриминант квадратного уравнения меньше нуля, D=-36, уравнение имеет пару комплексно сопряженных корней , k_1,2=

(α=2, β=3) и общее решение уравнения имеет вид:

Пример 10.11. Найти частное решение дифференциального уравнения

y»-5y’+4y=0, удовлетворяющее начальным условиям у'(0)=8, у(0)=5.

Решение. Сначала найдем общее решение, для этого составим

Дискриминант этого уравнения D=1, следовательно, уравнение имеет два действительный корня, k₁ = 2, k₂ = 3 и общее решение уравнения имеет вид:

Чтобы найти частное решение, сначала найдем у’=2С₁e 2 x +3C₂e 3 x , а затем подставим в общее решение и в производную от функции-решения у начальные условия и получим систему для определения постоянных С₁ и С₂ .

.

Таким образом искомое частное решение имеет вид: y =7e 2 x – 2e 3 x .

Не нашли, что искали? Воспользуйтесь поиском:

Видео:Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

Однородные дифференциальные уравнения второго порядка с постоянными коэффициентами

Однородные линейные дифференциальные уравнения второго порядка с постоянными коэффициентами имеют вид

где p и q — действительные числа. Рассмотрим на примерах, как решаются однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.

Решение линейного однородного однородного дифференциального уравнения второго порядка зависит от корней характеристического уравнения. Характеристическое уравнение — это уравнение k²+pk+q=0.

1) Если корни характеристического уравнения — различные действительные числа:

то общее решение линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами имеет вид

2) Если корни характеристического уравнения — равные действительные числа

(например, при дискриминанте, равном нулю), то общее решение однородного дифференциального уравнения второго порядка есть

3) Если корни характеристического уравнения — комплексные числа

(например, при дискриминанте, равном отрицательному числу), то общее решение однородного дифференциального уравнения второго порядка записывается в виде

Примеры решения линейных однородных дифференциальных уравнений второго порядка с постоянными коэффициентами

Найти общие решения однородных дифференциальных уравнений второго порядка:

Составляем характеристическое уравнение: k²-7k+12=0. Его дискриминант D=b²-4ac=1>0, поэтому корни — различные действительные числа.

Отсюда, общее решение этого однородного ДУ 2-го порядка есть

Составим и решим характеристическое уравнение:

Корни действительные и различные. Отсюда имеем общее решение данного однородного дифференциального уравнения:

В этом случае характеристическое уравнение

Корни различны и действительны. Поэтому общее решение однородного дифференциального уравнения 2-го порядка здесь

Поскольку корни действительны и равны, для этого дифференциального уравнения общее решение записываем как

Характеристическое уравнение здесь

Так как дискриминант — отрицательное число, корни характеристического уравнения — комплексные числа.

Общее решение этого однородного дифференциального уравнения второго порядка имеет вид

Отсюда находим общее решение данного диф. уравнения:

Примеры для самопроверки.

Найти общее решение однородных дифференциальных уравнений второго порядка с постоянными коэффициентами:

Видео:Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами

Данная статья рассматривает способы решения линейных дифференциальных однородных уравнений второго порядка с постоянными коэффициентами вида y » + p y ‘ + q y = 0 с p и q являющимися действительными числами. Будет рассмотрена теория с приведением примеров с подробным решением.

Перейдем к формулировке теоремы, которая показывает, какого вида должно быть уравнение, чтобы можно было искать общее решение ЛОДУ.

Видео:Как решать любое квадратное уравнение Полное Неполное квадр ур x^2+2x-3=0 5x^2-2x=0 2x^2-2=0 3x^2=0Скачать

Теорема общего решения линейного однородного дифференциального уравнения

Общим решением линейного однородного дифференциального уравнения вида y ( n ) + f n — 1 ( x ) · y ( n — 1 ) + . . . + f 0 ( x ) · y = 0 с непрерывными на интервале интегрирования x коэффициентами f 0 ( x ) , f 1 ( x ) , . . . , f n — 1 ( x ) определяют линейную комбинацию вида y 0 = ∑ j = 1 n C j · y j , где y j , j = 1 , 2 , . . . , n являются линейно независимыми частными решениями ЛОДУ на интервале x , где C j , j = 1 , 2 , . . . , n берут за произвольные постоянные.

Отсюда получаем, что общее решение такого уравнения y » + p y ‘ + q y = 0 может быть записано как y 0 = C 1 ⋅ y 1 + C 2 ⋅ y 2 , где y 1 и y 2 выражаются линейно независимыми решениями, а С 1 и C 2 – произвольными постоянными. Необходимо поработать с нахождением частных решений y 1 и y 2 .

Существует формула по Эйлеру для поиска частных решений вида y = e k · x .

Если взять y = e k · x за частное решение ЛОДУ второго порядка с постоянными коэффициентами y » + p y ‘ + q y = 0 , тогда, используя подстановку, получим тождество вида:

e k · x » + p · e k · x ‘ + q · e k · x = 0 k 2 · e k · x + p · e k · x + q · e k · x = 0 e k · x · ( k 2 + p · k + q ) = 0 k 2 + p · k + q = 0

Данное тождество называют характеристическим уравнением с постоянными коэффициентами k 1 и k 2 , которые и являются его решениями и определяют частые решения вида y 1 = e k 1 · x и y 2 = e k 2 · x заданного ЛОДУ.

При различных значениях p и q можно получить характеристические уравнения с корнами такого вида:

1. Действительные и различные k 1 ≠ k 2 , k 1 , k 2 ∈ R .
2. Действительные и совпадающие k 1 = k 2 , = k 0 , k 0 ∈ R .
3. Комплексно сопряженную пару k 1 = α + i · β , k 2 = α — i · β .

Первый случай показывает, что решениями такого уравнения могут быть y 1 = e k 1 · x и y 2 = e k 2 · x , а общее решение принимает вид y 0 = C 1 · e k 1 · x + C 2 · e k 2 · x с постоянными коэффициентами. Функции y 1 = e k 1 · x и y 2 = e k 2 · x рассматриваются, как линейно независимыми по причине отличного от нуля определителя Вронского W ( x ) = y 1 y 2 y 1 ‘ y 2 ‘ = e k 1 · x e k 2 · x k 1 · e k 1 · x k 2 · e k 2 · x = e k 1 · x · e k 2 · x · k 2 — k 1 с действительными k 1 ≠ k 2 , k 1 , k 2 ∈ R .

Второй случай объясняет, что первым частным решением функции – это выражение y 1 = e k 0 · x . Вторым частным решением можно брать y 2 = x · e k 0 · x . Определим, что y 2 = x · e k 0 · x может являться частным решением ЛОДУ второго порядка с постоянными коэффициентами y » + p y ‘ + q y = 0 и докажем линейную независимость y 1 и y 2 .

Имеем, что k 1 = k 0 и k 2 = k 0 являются совпадающими корнями характеристического уравнения. Тогда оно примет вид k — k 0 2 = 0 ⇔ k 2 — 2 k 0 · k + k 0 2 = 0 . Отсюда следует, что y » — 2 k 0 · y ‘ + k 0 2 · y = 0 является линейным однородным дифференциальным уравнением. Необходимо подставить выражение y 2 = x · e k 0 · x для того, чтобы убедиться в тождественности:

y 2 » — 2 k 0 · y ‘ 2 + k 0 2 · y 2 = 0 x · e k 0 · x » — 2 k 0 · x · e k 0 x ‘ + k 0 2 · x · e k 0 · x = 0 e k 0 · x + k 0 · x · e k 0 x ‘ — 2 k 0 · e k 0 · x + k 0 · x · e k 0 x + k 0 2 · x · e k 0 · x = 0 ( k 0 · e k 0 · x + k 0 · e k 0 · x + k 0 2 · x · e k 0 · x — — 2 k 0 · e k 0 · x — k 0 2 · x · e k 0 · x + k 0 2 · x · e k 0 · x ) = 0 0 ≡ 0

Отсюда следует, что y 2 = x · e k 0 · x — это частное решение данного уравнения. Необходимо рассмотреть линейную независимость y 1 = e k 0 · x и y 2 = x · e k 0 · x . Чтобы убедиться в этом, следует прибегнуть к вычислению определителя Вронского. Он не должен быть равен нулю.

W ( x ) = y 1 y 2 y 1 ‘ y 2 ‘ = e k 0 · x x · e k 0 · x e k 0 · x ‘ x · e k 0 · x ‘ = = e k 0 · x x · e k 0 · x k 0 · e k 0 · x e k 0 · x · ( 1 + k 0 · x ) = = e k 0 · x · e k 0 · x · 1 + k 0 · x — k 0 · x · e k 0 · x · e k 0 · x = e 2 k 0 · x ≠ 0 ∀ x ∈ R

Можно сделать вывод, что линейно независимые частные решения ЛОДУ второго порядка с постоянными коэффициентами y » + p y ‘ + q y = 0 считаются y 1 = e k 0 · x и y 2 = x · e k 0 · x . Это подразумевает то, что решением будет являться выражение y 0 = C 1 · e k 0 · x + C 2 · x · e k 0 · x при k 1 = k 2 = k 0 , k 0 ∈ R .

Третий случай говорит о том, что имеем дело с парой комплексных частных решений ЛОДУ вида y 1 = e α + i · β · x и y 2 = e α — i · β · x .

Запись общего решения примет вид y 0 = C 1 · e α + i · β · x + C 2 · e α — i · β · x .

Функции y 1 = e a · x · cos β x и y 2 = e a · x · sin β x могут быть записаны вместо частных решений уравнения, причем с соответствующими действительной и мнимой частями. Это понятно при преобразовании общего решения y 0 = C 1 · e α + i · β · x + C 2 · e α — i · β · x . Для этого необходимо воспользоваться формулами из теории функции комплексного переменного вида. Тогда получим, что

y 0 = C 1 · e α + i · β · x + C 2 · e α — i · β · x = = C 1 · e α · x · cos β x + i · sin β x + C 2 · e α · x · cos β x — i · sin β x = = ( C 1 + C 2 ) · e α · x · cos β x + i · ( C 1 — C 2 ) · e α · x · sin β x = = C 3 · e α · x · cos β x + C 4 · e α · x · sin β x

Отчетливо видно, что С 3 и С 4 используются в качестве произвольных постоянных.

Видео:Операционное исчисление. Решить неоднородное дифференциальное уравнение 2 порядкаСкачать

Алгоритм нахождения общего решения линейного однородного дифференциального уравнения

Алгоритм нахождения общего решения линейного однородного дифференциального уравнения 2 порядка с постоянными переменными вида y » + p y ‘ + q y = 0 :

1. Запись характеристического уравнения k 2 + p ⋅ k + q = 0 .
2. Нахождение корней характеристического уравнения k 1 и k 2 .
3. Производим запись ЛОДУ, исходя из полученных значений с постоянными коэффициентами:

• y 0 = C 1 · e k 1 · x + C 2 · e k 2 · x при k 1 ≠ k 2 , k 1 , k 2 ∈ R ;
• y 0 = C 1 · e k 0 · x + C 2 · x · e k 0 · x при k 1 = k 2 = k 0 , k 0 ∈ R ;
• y 0 = e α · x · ( C 1 · cos β x + C 2 · sin β x ) при k 1 = α + i · β , k 2 = α — i · β .

Найти общее решение заданного уравнения с постоянными коэффициентами y » + 4 y ‘ + 4 y = 0 .

Решение

Следуя алгоритму, необходимо записать характеристическое уравнение k 2 + 4 ⋅ k + 4 = 0 , после чего обозначить его корни. Получаем, что

k 2 + 4 k + 4 = 0 ( k + 2 ) 2 = 0 k 1 = k 2 = k 0 = — 2

Очевидно, что полученные корни являются совпадающими.

Ответ: Запись общего решения: y 0 = C 1 · e k 0 x + C 2 · x · e k 0 x = C 1 · e — 2 x + C 2 · x · e — 2 x .

Найти решение заданного уравнения вида y » — 5 y ‘ + 6 y = 0 .

Решение

По условию имеется ЛОДУ 2 порядка с постоянными коэффициентами. Это указывает на то, что необходимо записать характеристическое уравнение и обозначить его корни. Получим:

k 2 — 5 k + 6 = 0 D = 5 2 — 4 · 6 = 1 k 1 = 5 — 1 2 = 2 k 2 = 5 + 1 2 = 3

Видно, что корни различные и действительные. Это говорит о том, что уравнение общего вида запишется как y 0 = C 1 · e k 1 x + C 2 e k 2 x = C 1 · e 2 x + C 2 · e 3 x .

Ответ: y 0 = C 1 · e k 1 x + C 2 e k 2 x = C 1 · e 2 x + C 2 · e 3 x .

Найти общее решение дифференциального уравнения вида y » — y ‘ + 3 y = 0 .

Решение

Необходимо перейти к характеристическому уравнению ЛОДУ 2 порядка, что соответствует записи k 2 — k + 3 = 0 , после чего обозначить его корни. Тогда получим, что

D = 1 2 — 4 · 3 = — 11 k 1 = 1 + i 11 2 = 1 2 + i · 11 2 k 2 = 1 — i 11 2 = 1 2 — i · 11 2 ⇒ α = 1 2 , β = 11 2

На выходе имеем пару комплексно сопряженных корней характеристического уравнения. Отсюда следует, что общим решением является запись уравнения вида

y 0 = e a · x · ( C 1 · cos β x + C 2 · sin β x ) = = e x 2 · C 1 · cos 11 x 2 + C 2 · sin 11 2

Ответ: y 0 = e x 2 · C 1 · cos 11 x 2 + C 2 · sin 11 2 .

🌟 Видео

14. Дифференциальные уравнения второго порядка, допускающие понижение порядкаСкачать

Линейное однородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами.Скачать

РАЗБИРАЕМ ДИСКРИМИНАНТ ЧАСТЬ I #shorts #математика #егэ #огэ #дискриминантСкачать

18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Решение однородного дифференциального уравнения. Практическая часть. 11 класс.Скачать

Линейное неоднородное дифференциальное уравнение 2 способаСкачать

Дифференциальные уравнения, 8 урок, Линейные дифференциальные уравнения с const коэф-ами 2 порядкаСкачать

16. Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентамиСкачать

Решите уравнение ★ y'-2y=e^(2x) ★ Линейное дифференциальное уравнение 1-го порядкаСкачать

Дифференциальное уравнение от Бермана ★ Решите дифференциальное уравнение 2-го порядка ★ xy''=y'Скачать

Дифференциальные уравнения, 2 урок, Дифференциальные уравнения с разделяющимися переменнымиСкачать

13. Как решить дифференциальное уравнение первого порядка?Скачать

Дифференциальные уравнения | ЛОДУ 2-ого порядка с пост. коэфф. | общая схемаСкачать

Линейное неоднородное дифференциальное уравнение с постоянными коэффициентами 4y''-y=x^3-24x #1Скачать