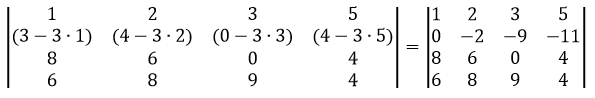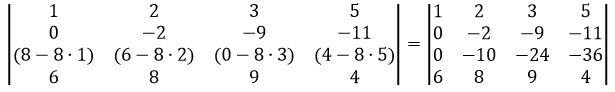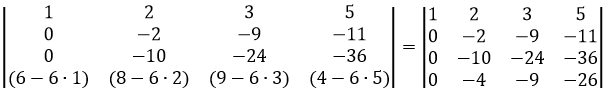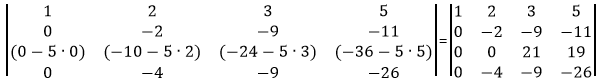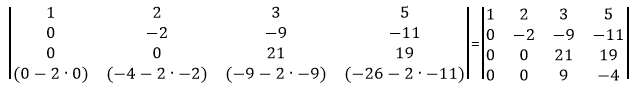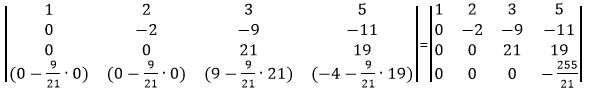Данная статья является первой частью серии статей под названием «Решение матриц». Каждая часть сопровождается теорией, примерами и подробным описанием.
Если Вам нужно привести матрицу к треугольному (ступенчатому) виду, воспользуйтесь нашим онлайн калькулятором.
- Содержание:
- Введение
- Описание алгоритма
- Пример приведения матрицы к треугольному виду
- Заключение
- Приведение матрицы к треугольному виду
- Приведение матрицы к треугольному виду (метод Гаусса)
- Приведение матрицы к треугольному виду (метод Барейса)
- Приведение определителя матрицы к треугольному виду
- Пример
- 📺 Видео
Видео:Приведение определителя к треугольному видуСкачать
Содержание:
Видео:Как привести матрицу к ступенчатому виду - bezbotvyСкачать
Введение
Эту задачу приходится решать очень часто, так как она используется во многих операциях над матрицами (решение систем линейных алгебраических уравнений (СЛАУ), вычисление определителя матрицы).
Что бы привести матрицу к треугольному виду, нужно воспользоваться методом Гаусса, который является простым в использовании и позволяет быстро прийти к конечному результату. Метод заключается в том чтобы исходную матрицу, путём элементарных преобразований привести к треугольному (ступенчатому) виду.
Видео:§16 Приведение определителей к треугольному видуСкачать
Описание алгоритма
Для приведения матрицы к треугольному виду, необходимо обнулить все элементы стоящие ниже главной диагонали.
Пусть дана матрица
.
Первым действием обнуляем первые элементы 2,3. n строки, для этого вычтем из этих строк первую строку умноженную на 
соответственно,
получим 
,
где 
.
Теперь вычтем из 3,4. n строки вторую строку умноженную на 
, этим действием обнуляем вторые элементы этих строк, соответственно, получаем
,
где bij элементы получившиеся в результате этих преобразований. И так далее, пока не получим вид 
,
где bij это элементы получившиеся в результате элементарных преобразований, это и есть матрица треугольного вида.
Видео:Алгоритм приведения матрицы к треугольному видуСкачать
Пример приведения матрицы к треугольному виду
Видео:Математика без Ху!ни. Метод Гаусса.Скачать
Заключение
Если Вам не понятен какой-либо шаг или у Вас есть вопросы по приведению матрицы к треугольному (ступенчатому) виду, вы всегда можете оставить свой комментарий ниже или решить её воспользовавшись нашим онлайн калькулятором.
Свои вопросы по данной статье, Вы всегда можете задать в комментариях.
Видео:Приведение матрицы к ступенчатому виду. Алгоритм ГауссаСкачать
Приведение матрицы к треугольному виду
Приведение матрицы к треугольному виду методом Гаусса и методом Барейса.
Ниже два калькулятора для приведения матриц к треугольному, или ступенчатому, виду. Первый использует для этого метод Гаусса, второй — метод Барейса. Описание методов и немного теории — под калькуляторами.
Приведение матрицы к треугольному виду (метод Гаусса)
Приведение матрицы к треугольному виду (метод Барейса)
Итак, для начала определимся с понятием треугольной, или ступенчатой матрицы:
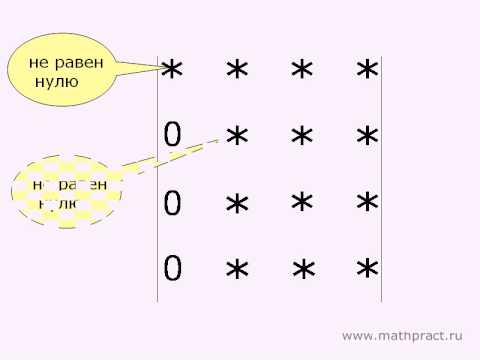
Матрица имеет ступенчатый вид, если:
- Все нулевые строки матрицы стоят последними
- Первый ненулевой элемент строки всегда находится строго правее первого ненулевого элемента предыдущей строки
- Все элементы столбца под первым ненулевым элементом строки равны нулю (это впрочем следует из первых двух пунктов)
Пример ступенчатой матрицы:
1 0 2 5
0 3 0 0
0 0 0 4
Понятие треугольной матрицы более узкое, оно используется только для квадратных матриц (хотя я думаю, что это не строго), и формулируется проще: треугольная матрица — квадратная матрица, в которой все элементы ниже главной диагонали равны нулю. Строго говоря, это даже определение верхнетреугольной матрицы, но мы будем использовать его. Понятно, что такая верхнетреугольная матрица является также и ступенчатой.
Пример треугольной (верхнетреугольной) матрицы:
1 0 2 5
0 3 1 3
0 0 4 2
0 0 0 3
Кстати, определитель треугольной матрицы вычисляется простым перемножением ее диагональных элементов.
Чем же так интересны ступенчатые (и треугольные) матрицы, что к ним надо приводить все остальные? — спросите вы.
У них есть замечательной свойство, а именно, любую прямоугольную матрицу можно с помощью элементарных преобразований привести к ступенчатой форме.
Что же такое элементарные преобразования? — спросите вы.
Элементарными преобразованиями матрицы называют следующие операции:
- перестановка любых двух строк (столбцов) матрицы
- умножение любой строки (столбца) на призвольное, отличное от нуля, число
- сложение любой строки (столбца) с другой строкой (столбцом), умноженной (умноженным) на произвольное, отличное от нуля, число.
И что? — спросите вы.
А то, что элементарные преобразования матрицы сохраняют эквивалентность матриц. А если вспомнить, что системы линейных алгебраический уравнений (СЛАУ) записывают как раз в матричной форме, то это означает, что элементарные преобразования матрицы не изменяют множество решений системы линейных алгебраических уравнений, которую представляет эта матрица.
Приведя матрицу системы линейных уравнений AX=B к треугольной форме A’X = B’, то есть, с соответствующими преобразованиями столбца B, можно найти решение этой системы так называемым «обратным ходом».
Чтобы было понятно, используем треугольную матрицу выше и перепишем систему уравнений в более привычной форме (столбец B я придумал сам):
Понятно, что сначала мы найдем , потом, подставив его в предыдущее уравнение, найдем и так далее — двигаясь от последнего уравнения к первому. Это и есть обратный ход.
Алгоритм приведения матрицы к ступенчатой форме с помощью элементарных преобразований называют методом Гаусса. Метод Гаусса — классический метод решения систем линейных алгебраических уравнений. Также его еще называют Гауссовым исключением, так как это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к эквивалентной системе ступенчатого (или треугольного) вида, из которого последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные.
Теперь про сам метод.
Собственно, как можно занулить переменную во втором уравнении? Вычтя из него первое, домноженное на коэффициент
Поясним на примере:
Зануляем во втором уравнении:
Во втором уравнении больше не содержится
Обобщенно алгоритм метода Гаусса можно представить следующим образом:
где N — число строк,
— i-тая строка,
— элемент, находящийся в i-той строке, j-том столбце
И все бы ничего, да и метод отличный, но. Дело все в делении на , присутствующем в формуле. Во-первых, если диагональный элемент будет равен нулю, то метод работать не будет. Во-вторых, в процессе вычисления будет накапливаться погрешность, и чем дальше, тем больше. Результат будет отличаться от точного.
Для уменьшения погрешности используют модификации метода Гаусса, которые основаны на том, что погрешность тем меньше, чем больше знаменатель дроби. Эти модификации — метод Гаусса с выбором максимума в столбце и метод Гаусса с выбором максимума по всей матрице. Как следует из названия, перед каждым шагом исключения переменной по столбцу (всей матрице) ищется элемент с максимальным значением и проводится перестановка строк (строк и столбцов), таким образом, чтобы он оказался на месте .
Но есть еще более радикальная модификация метода Гаусса, которая называется методом Барейса (Bareiss).
Как можно избавиться от деления? Например, умножив перед вычитанием строку на . Тогда вычитать надо будет строку , домноженную только на , без всякого деления.
.
Уже хорошо, но возникает проблема с ростом значений элементов матрицы в ходе вычисления.
Барейс предложил делить выражение выше на и показал, что если исходные элементы матрицы — целые числа, то результатом вычисления такого выражения тоже будет целое число. При этом принимается, что для нулевой строки .
Кстати, то, что в случае целочисленных элементов исходной матрицы алгоритм Барейса приводит к треугольной матрице с целочисленными элементами, то есть без накопления погрешности вычислений — довольно важное свойство с точки зрения машинной арифметики.
Алгоритм Барейса можно представить следующим образом:
Алгоритм, аналогично методу Гаусса, также можно улучшить поиском максимума по столбцу(всей матрице) и перестановкой соответствующих строк (строк и столбцов).
Видео:Определитель 5 порядка приводим к треугольному видуСкачать
Приведение определителя матрицы к треугольному виду
Для того что бы вычислить определитель матрицы четвертого порядка или выше можно разложить определитель по строке или столбцу или применить метод Гаусса и привести определитель к треугольному виду. Рассмотрим приведение определителя матрицы к треугольному виду.
Для того чтобы привести матрицу к треугольному используйте свойства определителя для элементарных преобразований над строками и столбцами. Для нахождения определителя нужно умножить все элементы на главной диагонали.
Видео:Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать
Пример
Найдем определитель матрицы четвертого порядка.
Сделаем элемент a2,1 равный нулю.
Из строки №2 вычтем строку №1, умноженную на 1 элемент строки №2, т.е. на 3
Сделаем элемент a3,1 равный нулю.
Из строки №3 вычтем строку №1, умноженную на 1 элемент строки №3, т.е. на 8
Сделаем элемент a4,1 равный нулю.
Из строки №4 вычтем строку №1, умноженную на 1 элемент строки №4, т.е. на 6
Сделаем элемент a3,2 равный нулю.
Из строки №3 вычитаем строку №2, умноженную на 5
Сделаем элемент a4,2 равный нулю.
Из строки №4 вычитаем строку №2, умноженную на 2
Сделаем элемент a4,3 равный нулю.
Из строки №4 вычтем строку №3, умноженную на 9/21.
Умножим элементы матрицы находящиеся на диагонали.
📺 Видео
5. Вычисление определителя методом приведения матрицы определителя к треугольному видуСкачать
Приведение матрицы к треугольному видуСкачать
5 способов вычисления определителя ★ Какой способ лучше?Скачать
Приведение матрицы к ступенчатому видуСкачать
Решение системы уравнений методом ГауссаСкачать
Ранг матрицыСкачать
Решение системы уравнений методом Гаусса 4x4Скачать
Элементарные преобразования матриц. Высшая математика.Скачать
Диагональный вид матрицы. Приведение матрицы к диагональному виду. Собственные векторыСкачать
Ранг матрицыСкачать
Как вычислить определитель матрицы четвертого порядка | Высшая математикаСкачать
Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать
