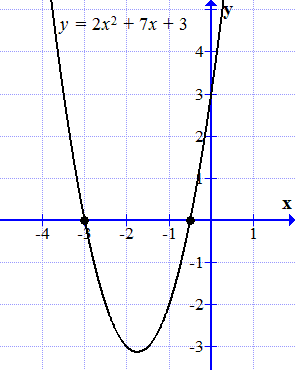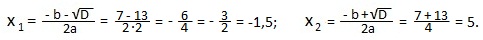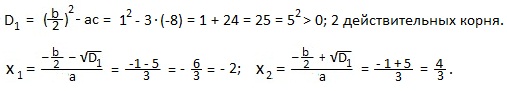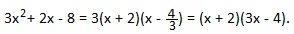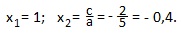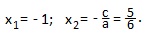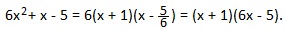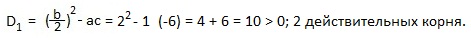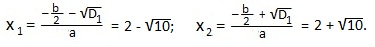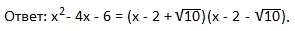Как представить квадратное уравнение в виде произведения корней

Видео:Квадратный Трехчлен / Разложение квадратного трехчлена на множители, Как решать Квадратные УравненияСкачать

Основные формулы

Рассмотрим квадратное уравнение:
(1) .
Корни квадратного уравнения (1) определяются по формулам:
; .
Эти формулы можно объединить так:
.
Когда корни квадратного уравнения известны, то многочлен второй степени можно представить в виде произведения сомножителей (разложить на множители):
.

Далее считаем, что – действительные числа.
Рассмотрим дискриминант квадратного уравнения:
.
Если дискриминант положителен, , то квадратное уравнение (1) имеет два различных действительных корня:
; .
Тогда разложение квадратного трехчлена на множители имеет вид:
.
Если дискриминант равен нулю, , то квадратное уравнение (1) имеет два кратных (равных) действительных корня:
.
Разложение на множители:
.
Если дискриминант отрицателен, , то квадратное уравнение (1) имеет два комплексно сопряженных корня:
;
.
Здесь – мнимая единица, ;
и – действительная и мнимая части корней:
; .
Тогда

.

Видео:Как разобраться в корнях ? Квадратный корень 8 класс | Математика TutorOnlineСкачать

Графическая интерпретация

Если построить график функции
,
который является параболой, то точки пересечения графика с осью будут корнями уравнения
.
При , график пересекает ось абсцисс (ось ) в двух точках (см. рисунок ⇓).
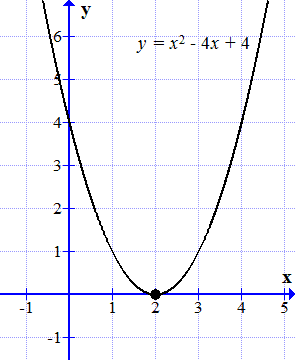
При , график касается оси абсцисс в одной точке (см. рисунок ⇓).
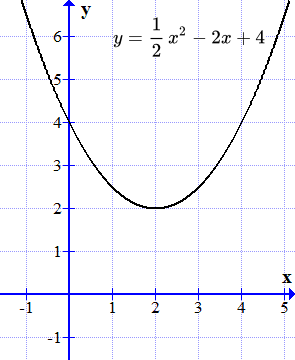
При , график не пересекает ось абсцисс (см. рисунок ⇓).

Видео:Решение квадратных уравнений. Дискриминант. 8 класс.Скачать

Полезные формулы, связанные с квадратным уравнением

Видео:Формула корней квадратного уравнения. Алгебра, 8 классСкачать

Вывод формулы для корней квадратного уравнения

Выполняем преобразования и применяем формулы (f.1) и (f.3):

,
где
; .

Итак, мы получили формулу для многочлена второй степени в виде:
.
Отсюда видно, что уравнение

выполняется при
и .
То есть и являются корнями квадратного уравнения
.

Видео:Метод выделения полного квадрата. 8 класс.Скачать

Примеры определения корней квадратного уравнения

Пример 1

Найти корни квадратного уравнения:
(1.1) .

Запишем квадратное уравнение в общем виде:
.
Сравнивая с нашим уравнением (1.1), находим значения коэффициентов:
.
Находим дискриминант:
.
Поскольку дискриминант положителен, , то уравнение имеет два действительных корня:
;
;
.

Отсюда получаем разложение квадратного трехчлена на множители:

.

График функции y = 2 x 2 + 7 x + 3 пересекает ось абсцисс в двух точках.

Построим график функции
.
График этой функции является параболой. Она пересевает ось абсцисс (ось ) в двух точках:
и .
Эти точки являются корнями исходного уравнения (1.1).

Пример 2

Найти корни квадратного уравнения:
(2.1) .

Запишем квадратное уравнение в общем виде:
.
Сравнивая с исходным уравнением (2.1), находим значения коэффициентов:
.
Находим дискриминант:
.
Поскольку дискриминант равен нулю, , то уравнение имеет два кратных (равных) корня:
;
.

Тогда разложение трехчлена на множители имеет вид:
.

График функции y = x 2 – 4 x + 4 касается оси абсцисс в одной точке.

Построим график функции
.
График этой функции является параболой. Она касается оси абсцисс (ось ) в одной точке:
.
Эта точка является корнем исходного уравнения (2.1). Поскольку этот корень входит в разложение на множители два раза:
,
то такой корень принято называть кратным. То есть считают, что имеется два равных корня:
.

Пример 3

Найти корни квадратного уравнения:
(3.1) .

Запишем квадратное уравнение в общем виде:
(1) .
Перепишем исходное уравнение (3.1):
.
Сравнивая с (1), находим значения коэффициентов:
.
Находим дискриминант:
.
Дискриминант отрицателен, . Поэтому действительных корней нет.

Можно найти комплексные корни:
;
;
.

График функции не пересекает ось абсцисс. Действительных корней нет.

Построим график функции
.
График этой функции является параболой. Она не пересекает ось абсцисс (ось ). Поэтому действительных корней нет.

Действительных корней нет. Корни комплексные:
;
;
.

Автор: Олег Одинцов . Опубликовано: 19-04-2016

Видео:Математика| Разложение квадратного трехчлена на множители.Скачать

8.2.5. Разложение квадратного трехчлена на линейные множители

Квадратный трехчлен ax 2 +bx+c можно разложить на линейные множители по формуле:

ax 2 +bx+c=a (x-x₁)(x-x₂), где x_1, x₂ — корни квадратного уравнения ax 2 +bx+c=0.

Разложить квадратный трехчлен на линейные множители:

Пример 1). 2x 2 -7x-15.

Решение. Найдем корни квадратного уравнения: 2x 2 -7x-15=0.

a=2; b=-7; c=-15. Это общий случай для полного квадратного уравнения. Находим дискриминант D.

D=b 2 -4ac=(-7) 2 -4∙2∙(-15)=49+120=169=13 2 >0; 2 действительных корня.

Применим формулу: ax 2 +bx+c=a (x-x₁)(x-x₂).

2x 2 -7x-15=2 (х+1,5)(х-5)=(2х+3)(х-5). Мы представили данный трехчлен 2x 2 -7x-15 в виде произведения двучленов 2х+3 и х-5.

Ответ: 2x 2 -7x-15=(2х+3)(х-5).

Пример 2). 3x 2 +2x-8.

Решение. Найдем корни квадратного уравнения:

a=3; b=2; c=-8. Это частный случай для полного квадратного уравнения с четным вторым коэффициентом (b=2). Находим дискриминант D₁.

Применим формулу: ax 2 +bx+c=a (x-x₁)(x-x₂).

Мы представили трехчлен 3x 2 +2x-8 в виде произведения двучленов х+2 и 3х-4.

Ответ: 3x 2 +2x-8=(х+2)(3х-4).

Пример 3). 5x 2 -3x-2.

Решение. Найдем корни квадратного уравнения:

a=5; b=-3; c=-2. Это частный случай для полного квадратного уравнения с выполненным условием: a+b+c=0 (5-3-2=0). В таких случаях первый корень всегда равен единице, а второй корень равен частному от деления свободного члена на первый коэффициент:

Применим формулу: ax 2 +bx+c=a (x-x₁)(x-x₂).

5x 2 -3x-2=5 (х-1)(х+0,4)=(х-1)(5х+2). Мы представили трехчлен 5x 2 -3x-2 в виде произведения двучленов х-1 и 5х+2.

Ответ: 5x 2 -3x-2=(х-1)(5х+2).

Пример 4). 6x 2 +x-5.

Решение. Найдем корни квадратного уравнения:

a=6; b=1; c=-5. Это частный случай для полного квадратного уравнения с выполненным условием: a-b+c=0 (6-1-5=0). В таких случаях первый корень всегда равен минус единице, а второй корень равен минус частному от деления свободного члена на первый коэффициент:

Применим формулу: ax 2 +bx+c=a (x-x₁)(x-x₂).

Мы представили трехчлен 6x 2 +x-5 в виде произведения двучленов х+1 и 6х-5.

Ответ: 6x 2 +x-5=(х+1)(6х-5).

Пример 5). x 2 -13x+12.

Решение. Найдем корни приведенного квадратного уравнения:

x 2 -13x+12=0. Проверим, можно ли применить теорему Виета. Для этого найдем дискриминант и убедимся, что он является полным квадратом целого числа.

a=1; b=-13; c=12. Находим дискриминант D.

D=b 2 -4ac=13 2 -4∙1∙12=169-48=121=11 2 .

Применим теорему Виета: сумма корней должна быть равна второму коэффициенту, взятому с противоположным знаком, а произведение корней должно быть равно свободному члену:

Применим формулу: ax 2 +bx+c=a (x-x₁)(x-x₂).

Ответ: x 2 -13x+12=(х-1)(х-12).

Пример 6). x 2 -4x-6.

Решение. Найдем корни приведенного квадратного уравнения:

a=1; b=-4; c=-6. Второй коэффициент — четное число. Находим дискриминант D₁.

Дискриминант не является полным квадратом целого числа, поэтому, теорема Виета нам не поможет, и мы найдем корни по формулам для четного второго коэффициента:

Применим формулу: ax 2 +bx+c=a (x-x₁)(x-x₂) и запишем ответ:

Друзья, для того, чтобы разложить квадратные трехчлены на множители, мы решали каждое квадратное уравнение рациональным способом. Все эти способы мы рассмотрели ранее в теме: «Решение полных квадратных уравнений».

Видео:Квадратные уравнения от «А» до «Я». Классификация, решение и теорема Виета | МатематикаСкачать

Решение квадратных уравнений: формула корней, примеры

В продолжение темы «Решение уравнений» материал данной статьи познакомит вас с квадратными уравнениями.

Рассмотрим все подробно: суть и запись квадратного уравнения, зададим сопутствующие термины, разберем схему решения неполных и полных уравнений, познакомимся с формулой корней и дискриминантом, установим связи между корнями и коэффициентами, ну и конечно приведем наглядное решение практических примеров.

Видео:5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

Квадратное уравнение, его виды

Квадратное уравнение – это уравнение, записанное как a · x 2 + b · x + c = 0 , где x – переменная, a , b и c – некоторые числа, при этом a не есть нуль.

Зачастую квадратные уравнения также носят название уравнений второй степени, поскольку по сути квадратное уравнение есть алгебраическое уравнение второй степени.

Приведем пример для иллюстрации заданного определения: 9 · x 2 + 16 · x + 2 = 0 ; 7 , 5 · x 2 + 3 , 1 · x + 0 , 11 = 0 и т.п. – это квадратные уравнения.

Числа a , b и c – это коэффициенты квадратного уравнения a · x 2 + b · x + c = 0 , при этом коэффициент a носит название первого, или старшего, или коэффициента при x 2 , b – второго коэффициента, или коэффициента при x , а c называют свободным членом.

К примеру, в квадратном уравнении 6 · x 2 − 2 · x − 11 = 0 старший коэффициент равен 6 , второй коэффициент есть − 2 , а свободный член равен − 11 . Обратим внимание на тот факт, что, когда коэффициенты b и/или c являются отрицательными, то используется краткая форма записи вида 6 · x 2 − 2 · x − 11 = 0 , а не 6 · x 2 + ( − 2 ) · x + ( − 11 ) = 0 .

Уточним также такой аспект: если коэффициенты a и/или b равны 1 или − 1 , то явного участия в записи квадратного уравнения они могут не принимать, что объясняется особенностями записи указанных числовых коэффициентов. К примеру, в квадратном уравнении y 2 − y + 7 = 0 старший коэффициент равен 1 , а второй коэффициент есть − 1 .

Видео:Найти значение суммы и произведения корней квадратного уравненияСкачать

Приведенные и неприведенные квадратные уравнения

По значению первого коэффициента квадратные уравнения подразделяют на приведенные и неприведенные.

Приведенное квадратное уравнение – это квадратное уравнение, где старший коэффициент равен 1 . При иных значениях старшего коэффициента квадратное уравнение является неприведенным.

Приведем примеры: квадратные уравнения x 2 − 4 · x + 3 = 0 , x 2 − x − 4 5 = 0 являются приведенными, в каждом из которых старший коэффициент равен 1 .

9 · x 2 − x − 2 = 0 — неприведенное квадратное уравнение, где первый коэффициент отличен от 1 .

Любое неприведенное квадратное уравнение возможно преобразовать в приведенное уравнение, если разделить обе его части на первый коэффициент (равносильное преобразование). Преобразованное уравнение будет иметь такие же корни, как и заданное неприведенное уравнение или так же не иметь корней вовсе.

Рассмотрение конкретного примера позволит нам наглядно продемонстрировать выполнение перехода от неприведенного квадратного уравнения к приведенному.

Задано уравнение 6 · x 2 + 18 · x − 7 = 0 . Необходимо преобразовать исходное уравнение в приведенную форму.

Решение

Cогласно указанной выше схеме разделим обе части исходного уравнения на старший коэффициент 6 . Тогда получим: ( 6 · x 2 + 18 · x − 7 ) : 3 = 0 : 3 , и это то же самое, что: ( 6 · x 2 ) : 3 + ( 18 · x ) : 3 − 7 : 3 = 0 и далее: ( 6 : 6 ) · x 2 + ( 18 : 6 ) · x − 7 : 6 = 0 . Отсюда: x 2 + 3 · x — 1 1 6 = 0 . Таким образом, получено уравнение, равносильное заданному.

Ответ: x 2 + 3 · x — 1 1 6 = 0 .

Видео:Быстрый способ решения квадратного уравненияСкачать

Полные и неполные квадратные уравнения

Обратимся к определению квадратного уравнения. В нем мы уточнили, что a ≠ 0 . Подобное условие необходимо, чтобы уравнение a · x 2 + b · x + c = 0 было именно квадратным, поскольку при a = 0 оно по сути преобразуется в линейное уравнение b · x + c = 0 .

В случае же, когда коэффициенты b и c равны нулю (что возможно, как по отдельности, так и совместно), квадратное уравнение носит название неполного.

Неполное квадратное уравнение – такое квадратное уравнение a · x 2 + b · x + c = 0 , где хотя бы один из коэффициентов b и c (или оба) равен нулю.

Полное квадратное уравнение – квадратное уравнение, в котором все числовые коэффициенты не равны нулю.

Порассуждаем, почему типам квадратных уравнений даны именно такие названия.

При b = 0 квадратное уравнение примет вид a · x 2 + 0 · x + c = 0 , что то же самое, что a · x 2 + c = 0 . При c = 0 квадратное уравнение записано как a · x 2 + b · x + 0 = 0 , что равносильно a · x 2 + b · x = 0 . При b = 0 и c = 0 уравнение примет вид a · x 2 = 0 . Уравнения, которые мы получили, отличны от полного квадратного уравнения тем, что в их левых частях не содержится либо слагаемого с переменной x , либо свободного члена, либо обоих сразу. Собственно, этот факт и задал название такому типу уравнений – неполное.

Например, x 2 + 3 · x + 4 = 0 и − 7 · x 2 − 2 · x + 1 , 3 = 0 – это полные квадратные уравнения; x 2 = 0 , − 5 · x 2 = 0 ; 11 · x 2 + 2 = 0 , − x 2 − 6 · x = 0 – неполные квадратные уравнения.

Видео:Разложение квадратного трехчлена на множители. 8 класс.Скачать

Решение неполных квадратных уравнений

Заданное выше определение дает возможность выделить следующие виды неполных квадратных уравнений:

• a · x 2 = 0 , такому уравнению соответствуют коэффициенты b = 0 и c = 0 ;
• a · x 2 + c = 0 при b = 0 ;
• a · x 2 + b · x = 0 при c = 0 .

Рассмотрим последовательно решение каждого вида неполного квадратного уравнения.

Видео:Составьте квадратное уравнение, корнями которого являются числаСкачать

Решение уравнения a·x 2 =0

Как уже было указано выше, такому уравнению отвечают коэффициенты b и c , равные нулю. Уравнение a · x 2 = 0 возможно преобразовать в равносильное ему уравнение x 2 = 0 , которое мы получим, поделив обе части исходного уравнения на число a , не равное нулю. Очевидный факт, что корень уравнения x 2 = 0 это нуль, поскольку 0 2 = 0 . Иных корней это уравнение не имеет, что объяснимо свойствами степени: для любого числа p , не равного нулю, верно неравенство p 2 > 0 , из чего следует, что при p ≠ 0 равенство p 2 = 0 никогда не будет достигнуто.

Таким образом, для неполного квадратного уравнение a · x 2 = 0 существует единственный корень x = 0 .

Для примера решим неполное квадратное уравнение − 3 · x 2 = 0 . Ему равносильно уравнение x 2 = 0 , его единственным корнем является x = 0 , тогда и исходное уравнение имеет единственный корень — нуль.

Кратко решение оформляется так:

− 3 · x 2 = 0 , x 2 = 0 , x = 0 .

Видео:Теорема Виета. 8 класс.Скачать

Решение уравнения a · x 2 + c = 0

На очереди — решение неполных квадратных уравнений, где b = 0 , c ≠ 0 , то есть уравнений вида a · x 2 + c = 0 . Преобразуем это уравнение, перенеся слагаемое из одной части уравнения в другую, сменив знак на противоположный и разделив обе части уравнения на число, не равное нулю:

• переносим c в правую часть, что дает уравнение a · x 2 = − c ;
• делим обе части уравнения на a , получаем в итоге x = — c a .

Наши преобразования являются равносильными, соответственно полученное уравнение также равносильно исходному, и этот факт дает возможность делать вывод о корнях уравнения. От того, каковы значения a и c зависит значение выражения — c a : оно может иметь знак минус (допустим, если a = 1 и c = 2 , тогда — c a = — 2 1 = — 2 ) или знак плюс (например, если a = − 2 и c = 6 , то — c a = — 6 — 2 = 3 ); оно не равно нулю, поскольку c ≠ 0 . Подробнее остановимся на ситуациях, когда — c a 0 и — c a > 0 .

В случае, когда — c a 0 , уравнение x 2 = — c a не будет иметь корней. Утверждая это, мы опираемся на то, что квадратом любого числа является число неотрицательное. Из сказанного следует, что при — c a 0 ни для какого числа p равенство p 2 = — c a не может быть верным.

Все иначе, когда — c a > 0 : вспомним о квадратном корне, и станет очевидно, что корнем уравнения x 2 = — c a будет число — c a , поскольку — c a 2 = — c a . Нетрудно понять, что число — — c a — также корень уравнения x 2 = — c a : действительно, — — c a 2 = — c a .

Прочих корней уравнение не будет иметь. Мы можем это продемонстрировать, используя метод от противного. Для начала зададим обозначения найденных выше корней как _{x 1} и _{− x 1} . Выскажем предположение, что уравнение x 2 = — c a имеет также корень x 2 , который отличается от корней _{x 1} и _{− x 1} . Мы знаем, что, подставив в уравнение вместо x его корни, преобразуем уравнение в справедливое числовое равенство.

Для _{x 1} и _{− x 1} запишем: x 1 2 = — c a , а для x 2 — x 2 2 = — c a . Опираясь на свойства числовых равенств, почленно вычтем одно верное равенство из другого, что даст нам: x 1 2 − x 2 2 = 0 . Используем свойства действий с числами, чтобы переписать последнее равенство как ( x 1 − x 2 ) · ( x 1 + x 2 ) = 0 . Известно, что произведение двух чисел есть нуль тогда и только тогда, когда хотя бы одно из чисел является нулем. Из сказанного следует, что x 1 − x 2 = 0 и/или x 1 + x 2 = 0 , что то же самое, x 2 = x 1 и/или x 2 = − x 1 . Возникло очевидное противоречие, ведь вначале было условлено, что корень уравнения x 2 отличается от _{x 1} и _{− x 1} . Так, мы доказали, что уравнение не имеет иных корней, кроме x = — c a и x = — — c a .

Резюмируем все рассуждения выше.

Неполное квадратное уравнение a · x 2 + c = 0 равносильно уравнению x 2 = — c a , которое:

• не будет иметь корней при — c a 0 ;
• будет иметь два корня x = — c a и x = — — c a при — c a > 0 .

Приведем примеры решения уравнений a · x 2 + c = 0 .

Задано квадратное уравнение 9 · x 2 + 7 = 0 . Необходимо найти его решение.

Решение

Перенесем свободный член в правую часть уравнения, тогда уравнение примет вид 9 · x 2 = − 7 .
Разделим обе части полученного уравнения на 9 , придем к x 2 = — 7 9 . В правой части мы видим число со знаком минус, что означает: у заданного уравнения нет корней. Тогда и исходное неполное квадратное уравнение 9 · x 2 + 7 = 0 не будет иметь корней.

Ответ: уравнение 9 · x 2 + 7 = 0 не имеет корней.

Необходимо решить уравнение − x 2 + 36 = 0 .

Решение

Перенесем 36 в правую часть: − x 2 = − 36 .
Разделим обе части на − 1 , получим x 2 = 36 . В правой части — положительное число, отсюда можно сделать вывод, что x = 36 или x = — 36 .
Извлечем корень и запишем окончательный итог: неполное квадратное уравнение − x 2 + 36 = 0 имеет два корня x = 6 или x = − 6 .

Ответ: x = 6 или x = − 6 .

Видео:Свойства квадратного корня. Уравнение х2=а, 8 классСкачать

Решение уравнения a·x 2 +b·x=0

Разберем третий вид неполных квадратных уравнений, когда c = 0 . Чтобы найти решение неполного квадратного уравнения a · x 2 + b · x = 0 , воспользуемся методом разложения на множители. Разложим на множители многочлен, который находится в левой части уравнения, вынеся за скобки общий множитель x . Этот шаг даст возможность преобразовать исходное неполное квадратное уравнение в равносильное ему x · ( a · x + b ) = 0 . А это уравнение, в свою очередь, равносильно совокупности уравнений x = 0 и a · x + b = 0 . Уравнение a · x + b = 0 линейное, и корень его: x = − b a .

Таким образом, неполное квадратное уравнение a · x 2 + b · x = 0 будет иметь два корня x = 0 и x = − b a .

Закрепим материал примером.

Необходимо найти решение уравнения 2 3 · x 2 — 2 2 7 · x = 0 .

Решение

Вынесем x за скобки и получим уравнение x · 2 3 · x — 2 2 7 = 0 . Это уравнение равносильно уравнениям x = 0 и 2 3 · x — 2 2 7 = 0 . Теперь следует решить полученное линейное уравнение: 2 3 · x = 2 2 7 , x = 2 2 7 2 3 .

Далее осуществим деление смешанного числа на обыкновенную дробь и определяем, что x = 3 3 7 . Таким образом, корни исходного уравнения это: x = 0 и x = 3 3 7 .

Кратко решение уравнения запишем так:

2 3 · x 2 — 2 2 7 · x = 0 x · 2 3 · x — 2 2 7 = 0

x = 0 или 2 3 · x — 2 2 7 = 0

x = 0 или x = 3 3 7

Ответ: x = 0 , x = 3 3 7 .

Видео:Произведение многочленов. Разложение многочлена на множители способом группировки. 7 класс.Скачать

Дискриминант, формула корней квадратного уравнения

Для нахождения решения квадратных уравнений существует формула корней:

x = — b ± D 2 · a , где D = b 2 − 4 · a · c – так называемый дискриминант квадратного уравнения.

Запись x = — b ± D 2 · a по сути означает, что x 1 = — b + D 2 · a , x 2 = — b — D 2 · a .

Нелишним будет понимать, как была выведена указанная формула и каким образом ее применять.

Видео:Решение квадратных уравнений. Метод разложения на множители. 8 класс.Скачать

Вывод формулы корней квадратного уравнения

Пускай перед нами стоит задача решить квадратное уравнение a · x 2 + b · x + c = 0 . Осуществим ряд равносильных преобразований:

• разделим обе части уравнения на число a, отличное от нуля, получим приведенное квадратное уравнение: x 2 + b a · x + c a = 0 ;
• выделим полный квадрат в левой части получившегося уравнения:
  x 2 + b a · x + c a = x 2 + 2 · b 2 · a · x + b 2 · a 2 — b 2 · a 2 + c a = = x + b 2 · a 2 — b 2 · a 2 + c a
  После этого уравнения примет вид: x + b 2 · a 2 — b 2 · a 2 + c a = 0 ;
• теперь возможно сделать перенос двух последних слагаемых в правую часть, сменив знак на противоположный, после чего получаем: x + b 2 · a 2 = b 2 · a 2 — c a ;
• наконец, преобразуем выражение, записанное в правой части последнего равенства:
  b 2 · a 2 — c a = b 2 4 · a 2 — c a = b 2 4 · a 2 — 4 · a · c 4 · a 2 = b 2 — 4 · a · c 4 · a 2 .

Таким образом, мы пришли к уравнению x + b 2 · a 2 = b 2 — 4 · a · c 4 · a 2 , равносильному исходному уравнению a · x 2 + b · x + c = 0 .

Решение подобных уравнений мы разбирали в предыдущих пунктах (решение неполных квадратных уравнений). Уже полученный опыт дает возможность сделать вывод касательно корней уравнения x + b 2 · a 2 = b 2 — 4 · a · c 4 · a 2 :

• при b 2 — 4 · a · c 4 · a 2 0 уравнение не имеет действительных решений;
• при b 2 — 4 · a · c 4 · a 2 = 0 уравнение имеет вид x + b 2 · a 2 = 0 , тогда x + b 2 · a = 0 .

Отсюда очевиден единственный корень x = — b 2 · a ;

• при b 2 — 4 · a · c 4 · a 2 > 0 верным будет: x + b 2 · a = b 2 — 4 · a · c 4 · a 2 или x = b 2 · a — b 2 — 4 · a · c 4 · a 2 , что то же самое, что x + — b 2 · a = b 2 — 4 · a · c 4 · a 2 или x = — b 2 · a — b 2 — 4 · a · c 4 · a 2 , т.е. уравнение имеет два корня.

Возможно сделать вывод, что наличие или отсутствие корней уравнения x + b 2 · a 2 = b 2 — 4 · a · c 4 · a 2 (а значит и исходного уравнения) зависит от знака выражения b 2 — 4 · a · c 4 · a 2 , записанного в правой части. А знак этого выражения задается знаком числителя, (знаменатель 4 · a 2 всегда будет положителен), то есть, знаком выражения b 2 − 4 · a · c . Этому выражению b 2 − 4 · a · c дано название — дискриминант квадратного уравнения и определена в качестве его обозначения буква D . Здесь можно записать суть дискриминанта – по его значению и знаку делают вывод, будет ли квадратное уравнение иметь действительные корни, и, если будет, то каково количество корней — один или два.

Вернемся к уравнению x + b 2 · a 2 = b 2 — 4 · a · c 4 · a 2 . Перепишем его, используя обозначение дискриминанта: x + b 2 · a 2 = D 4 · a 2 .

Вновь сформулируем выводы:

• при D 0 уравнение не имеет действительных корней;
• при D = 0 уравнение имеет единственный корень x = — b 2 · a ;
• при D > 0 уравнение имеет два корня: x = — b 2 · a + D 4 · a 2 или x = — b 2 · a — D 4 · a 2 . Эти корни на основе свойства радикалов возможно записать в виде: x = — b 2 · a + D 2 · a или — b 2 · a — D 2 · a . А, когда раскроем модули и приведем дроби к общему знаменателю, получим: x = — b + D 2 · a , x = — b — D 2 · a .

Так, результатом наших рассуждений стало выведение формулы корней квадратного уравнения:

x = — b + D 2 · a , x = — b — D 2 · a , дискриминант D вычисляется по формуле D = b 2 − 4 · a · c .

Данные формулы дают возможность при дискриминанте больше нуля определить оба действительных корня. Когда дискриминант равен нулю, применение обеих формул даст один и тот же корень, как единственное решение квадратного уравнения. В случае, когда дискриминант отрицателен, попытавшись использовать формулу корня квадратного уравнения, мы столкнемся с необходимостью извлечь квадратный корень из отрицательного числа, что выведет нас за рамки действительных чисел. При отрицательном дискриминанте у квадратного уравнения не будет действительных корней, но возможна пара комплексно сопряженных корней, определяемых теми же полученными нами формулами корней.

Видео:СЛОЖИТЕ ДВА КОРНЯСкачать

Алгоритм решения квадратных уравнений по формулам корней

Решить квадратное уравнение возможно, сразу задействуя формулу корней, но в основном так поступают при необходимости найти комплексные корни.

В основной же массе случаев обычно подразумевается поиск не комплексных, а действительных корней квадратного уравнения. Тогда оптимально перед тем, как использовать формулы корней квадратного уравнения, сначала определить дискриминант и удостовериться, что он не является отрицательным (в ином случае сделаем вывод, что у уравнения нет действительных корней), а после приступить к вычислению значения корней.

Рассуждения выше дают возможность сформулировать алгоритм решения квадратного уравнения.

Чтобы решить квадратное уравнение a · x 2 + b · x + c = 0 , необходимо:

• по формуле D = b 2 − 4 · a · c найти значение дискриминанта;
• при D 0 сделать вывод об отсутствии у квадратного уравнения действительных корней;
• при D = 0 найти единственный корень уравнения по формуле x = — b 2 · a ;
• при D > 0 определить два действительных корня квадратного уравнения по формуле x = — b ± D 2 · a .

Отметим, что, когда дискриминант есть нуль, можно использовать формулу x = — b ± D 2 · a , она даст тот же результат, что и формула x = — b 2 · a .

Видео:Квадратный корень. 8 класс.Скачать

Примеры решения квадратных уравнений

Приведем решение примеров при различных значениях дискриминанта.

Необходимо найти корни уравнения x 2 + 2 · x − 6 = 0 .

Решение

Запишем числовые коэффициенты квадратного уравнения: a = 1 , b = 2 и c = − 6 . Далее действуем по алгоритму, т.е. приступим к вычислению дискриминанта, для чего подставим коэффициенты a , b и c в формулу дискриминанта: D = b 2 − 4 · a · c = 2 2 − 4 · 1 · ( − 6 ) = 4 + 24 = 28 .

Итак, мы получили D > 0 , а это означает, что исходное уравнение будет иметь два действительных корня.
Для их нахождения используем формулу корня x = — b ± D 2 · a и, подставив соответствующие значения, получим: x = — 2 ± 28 2 · 1 . Упростим полученное выражение, вынеся множитель за знак корня с последующим сокращением дроби:

x = — 2 + 2 · 7 2 или x = — 2 — 2 · 7 2

x = — 1 + 7 или x = — 1 — 7

Ответ: x = — 1 + 7 ​​​​​​, x = — 1 — 7 .

Необходимо решить квадратное уравнение − 4 · x 2 + 28 · x − 49 = 0 .

Решение

Определим дискриминант: D = 28 2 − 4 · ( − 4 ) · ( − 49 ) = 784 − 784 = 0 . При таком значении дискриминанта исходное уравнение будет иметь лишь один корень, определяемый по формуле x = — b 2 · a .

x = — 28 2 · ( — 4 ) x = 3 , 5

Ответ: x = 3 , 5 .

Необходимо решить уравнение 5 · y 2 + 6 · y + 2 = 0

Решение

Числовые коэффициенты этого уравнения будут: a = 5 , b = 6 и c = 2 . Используем эти значения для нахождения дискриминанта: D = b 2 − 4 · a · c = 6 2 − 4 · 5 · 2 = 36 − 40 = − 4 . Вычисленный дискриминант отрицателен, таким образом, исходное квадратное уравнение не имеет действительных корней.

В случае, когда стоит задача указать комплексные корни, применим формулу корней, выполняя действия с комплексными числами:

x = — 6 + 2 · i 10 или x = — 6 — 2 · i 10 ,

x = — 3 5 + 1 5 · i или x = — 3 5 — 1 5 · i .

Ответ: действительные корни отсутствуют; комплексные корни следующие: — 3 5 + 1 5 · i , — 3 5 — 1 5 · i .

В школьной программе стандартно нет требования искать комплексные корни, поэтому, если в ходе решения дискриминант определен как отрицательный, сразу записывается ответ, что действительных корней нет.

Видео:Составление квадратных уравнений с помощью заданных корнейСкачать

Формула корней для четных вторых коэффициентов

Формула корней x = — b ± D 2 · a ( D = b 2 − 4 · a · c ) дает возможность получить еще одну формулу, более компактную, позволяющую находить решения квадратных уравнений с четным коэффициентом при x (либо с коэффициентом вида 2 · n , к примеру, 2 · 3 или 14 · ln 5 = 2 · 7 · ln 5 ). Покажем, как выводится эта формула.

Пусть перед нами стоит задача найти решение квадратного уравнения a · x 2 + 2 · n · x + c = 0 . Действуем по алгоритму: определяем дискриминант D = ( 2 · n ) 2 − 4 · a · c = 4 · n 2 − 4 · a · c = 4 · ( n 2 − a · c ) , а затем используем формулу корней:

x = — 2 · n ± D 2 · a , x = — 2 · n ± 4 · n 2 — a · c 2 · a , x = — 2 · n ± 2 n 2 — a · c 2 · a , x = — n ± n 2 — a · c a .

Пусть выражение n 2 − a · c будет обозначено как D 1 (иногда его обозначают D ‘ ). Тогда формула корней рассматриваемого квадратного уравнения со вторым коэффициентом 2 · n примет вид:

x = — n ± D 1 a , где D 1 = n 2 − a · c .

Легко увидеть, что что D = 4 · D 1 , или D 1 = D 4 . Иначе говоря, D 1 – это четверть дискриминанта. Очевидно, что знак D 1 такой же, как знак D , а значит знак D 1 также может служить индикатором наличия или отсутствия корней квадратного уравнения.

Таким образом, чтобы найти решение квадратного уравнения со вторым коэффициентом 2 · n , необходимо:

• найти D 1 = n 2 − a · c ;
• при D 1 0 сделать вывод, что действительных корней нет;
• при D 1 = 0 определить единственный корень уравнения по формуле x = — n a ;
• при D 1 > 0 определить два действительных корня по формуле x = — n ± D 1 a .

Необходимо решить квадратное уравнение 5 · x 2 − 6 · x − 32 = 0 .

Решение

Второй коэффициент заданного уравнения можем представить как 2 · ( − 3 ) . Тогда перепишем заданное квадратное уравнение как 5 · x 2 + 2 · ( − 3 ) · x − 32 = 0 , где a = 5 , n = − 3 и c = − 32 .

Вычислим четвертую часть дискриминанта: D 1 = n 2 − a · c = ( − 3 ) 2 − 5 · ( − 32 ) = 9 + 160 = 169 . Полученное значение положительно, это означает, что уравнение имеет два действительных корня. Определим их по соответствующей формуле корней:

x = — n ± D 1 a , x = — — 3 ± 169 5 , x = 3 ± 13 5 ,

x = 3 + 13 5 или x = 3 — 13 5

x = 3 1 5 или x = — 2

Возможно было бы произвести вычисления и по обычной формуле корней квадратного уравнения, но в таком случае решение было бы более громоздким.

Ответ: x = 3 1 5 или x = — 2 .

Видео:Свойства арифметического квадратного корня. 8 класс.Скачать

Упрощение вида квадратных уравнений

Иногда существует возможность оптимизировать вид исходного уравнения, что позволит упростить процесс вычисления корней.

К примеру, квадратное уравнение 12 · x 2 − 4 · x − 7 = 0 явно удобнее для решения, чем 1200 · x 2 − 400 · x − 700 = 0 .

Чаще упрощение вида квадратного уравнения производится действиями умножения или деления его обеих частей на некое число. К примеру, выше мы показали упрощенную запись уравнения 1200 · x 2 − 400 · x − 700 = 0 , полученную делением обеих его частей на 100 .

Такое преобразование возможно, когда коэффициенты квадратного уравнения не являются взаимно простыми числами. Тогда обычно осуществляют деление обеих частей уравнения на наибольший общий делитель абсолютных величин его коэффициентов.

Как пример используем квадратное уравнение 12 · x 2 − 42 · x + 48 = 0 . Определим НОД абсолютных величин его коэффициентов: НОД ( 12 , 42 , 48 ) = НОД(НОД ( 12 , 42 ) , 48 ) = НОД ( 6 , 48 ) = 6 . Произведем деление обеих частей исходного квадратного уравнения на 6 и получим равносильное ему квадратное уравнение 2 · x 2 − 7 · x + 8 = 0 .

Умножением обеих частей квадратного уравнения обычно избавляются от дробных коэффициентов. При этом умножают на наименьшее общее кратное знаменателей его коэффициентов. К примеру, если каждую часть квадратного уравнения 1 6 · x 2 + 2 3 · x — 3 = 0 перемножить с НОК ( 6 , 3 , 1 ) = 6 , то оно станет записано в более простом виде x 2 + 4 · x − 18 = 0 .

Напоследок отметим, что почти всегда избавляются от минуса при первом коэффициенте квадратного уравнения, изменяя знаки каждого члена уравнения, что достигается путем умножения (или деления) обеих частей на − 1 . К примеру, от квадратного уравнения − 2 · x 2 − 3 · x + 7 = 0 можно перейти к упрощенной его версии 2 · x 2 + 3 · x − 7 = 0 .

Связь между корнями и коэффициентами

Уже известная нам формула корней квадратных уравнений x = — b ± D 2 · a выражает корни уравнения через его числовые коэффициенты. Опираясь на данную формулу, мы имеем возможность задать другие зависимости между корнями и коэффициентами.

Самыми известными и применимыми являются формулы теоремы Виета:

x 1 + x 2 = — b a и x 2 = c a .

В частности, для приведенного квадратного уравнения сумма корней есть второй коэффициент с противоположным знаком, а произведение корней равно свободному члену. К примеру, по виду квадратного уравнения 3 · x 2 − 7 · x + 22 = 0 возможно сразу определить, что сумма его корней равна 7 3 , а произведение корней — 22 3 .

Также можно найти ряд прочих связей между корнями и коэффициентами квадратного уравнения. Например, сумма квадратов корней квадратного уравнения может быть выражена через коэффициенты:

x 1 2 + x 2 2 = ( x 1 + x 2 ) 2 — 2 · x 1 · x 2 = — b a 2 — 2 · c a = b 2 a 2 — 2 · c a = b 2 — 2 · a · c a 2 .