Численное решение дифференциальных уравнений с помощью команды dsolve. Построение графиков решений дифференциальных уравнений с помощью команды odeplot.
Для того, чтобы найти численное решение дифференциального уравнения (задачи Коши или краевой задачи) в команде dsolve следует указать параметр type=numeric (или просто numeric ). Тогда команда решения дифференциального уравнения будет иметь вид dsolve(eq, vars, type=numeric, options), где eq – уравнения, vars – список неизвестных функций, options – параметры, позволяющие указать метод численного интегрирования дифференциального уравнения. В Maple реализованы такие методы: method=rkf45 — метод Рунге-Кутта-Фельберга 4-5-ого порядка (установлен по умолчанию); method=dverk78 – метод Рунге-Кутта 7-8 порядка; mtthod=classical – классический метод Рунге-Кутта 3-его порядка; method=gear и method=mgear – одношаговый и многошаговый методы Гира.
График численного решения дифференциального уравнения можно построить с помощью команды odeplot(dd, [x,y(x)], x=x1..x2), где в качестве функции используется команда dd:=dsolve(, y(x), numeric) численного решения, после нее в квадратных скобках указывают переменную и неизвестную функцию [x,y(x)] , и интервал x=x1..x2 для построения графика.
Видео:Частное решение дифференциального уравнения. 11 класс.Скачать

Задание 2.1.
1. Найти численное и приближенное решение в виде степенного ряда до 6-ого порядка задачи Коши: 


Сначала найдем численное решение задачи Коши и построим его график.
de := proc ( rkf45_x ). end
Замечание : в строке вывода появляется сообщение о том, что при решении использован метод rkf45 . Во избежание вывода строк, не несущих полезной информации, рекомендуется отделять промежуточные команды двоеточием. Если необходимо получить значение решения при каком-то фиксированном значении переменной х (заодно будет выведено значение производной решения в этой точке), например, при х =0.5, то следует набрать:
Теперь найдем приближенное решение задачи Коши в виде степенного ряда и построим графики численного решения и полученного степенного ряда в интервале их наилучшего совпадения.
Наилучшее приближение решения степенным рядом достигается примерно на интервале — 1 x
х ‘( t )=2 y ( t )sin( t ) — х ( t ) — t ,
Пакет графического представления решений дифференциальных уравнений Detools .
Для численного решения задачи Коши, построения графиков решения и фазовых портретов в Maple имеется специальный пакет DEtools .
Команда DEplot из пакета DEtools строит численными методами графики решения или фазовые портреты. Эта команда аналогична команде odeplot , но более функциональна. Она, в отличие от odeplot , сама производит численное решение дифференциального уравнения. Основные параметры DEplot похожи на параметры odeplot : DEplot(de, vars, range, x=х1..х2, y=у1..у2, cond, ptions) , где de — дифференциальное уравнение или система дифференциальных уравнений; vars – список неизвестных функций; range – диапазон измерения независимой переменной; cond – начальные условия; x=х1..х2 и y=у1..у2 – диапазоны изменения функций; options – дополнительные параметры.
Наиболее часто используемые параметры: linecolor =цвет линии; scene=[x,y] — определяет, какие зависимости выводить на график; iterations =число итераций, необходимое для повышения точности вычислений (по умолчанию это число равно 1); stepsize =число, равное расстоянию между точками на графике, по умолчанию оно равно ( x2 — x1 )/20, этот параметр необходим для вывода более гладкой кривой решения; obsrange = true / false — прерывать или нет вычисления, если график решения выходит за установленный для рисования интервал.
Для решения дифференциального уравнения n -ого порядка начальные условия можно задавать в более компактной форме: [x0, y0, y ‘ 0, y » 0,…] , где x0 — точка, в которой задаются начальные условия, y0 — значение искомой функции в точке x0 , y ‘ 0, y » 0,… — значения производных первой, второй и т.д. до ( n — 1)-ого порядка.
Видео:Откуда появляются дифференциальные уравнения и как их решатьСкачать

Задание 2.2.
Нарисовать график решения дифференциального уравнения:





(D@@2)(y)(0)=1]], stepsize=.1, linecolor=black,
Построение фазовых портретов систем дифференциальных уравнений.
Для дифференциального уравнения порядка выше первого команда DEplot рисует только кривые решений дифференциальных уравнений, а для систем дифференциальных уравнений первого порядка могут быть нарисованы и фазовые портреты.
С помощью команды DEplot можно построить фазовый портрет в плоскости ( x , y ), для системы двух дифференциальных уравнений: 
Если система дифференциальных уравнений является автономной, то на фазовом портрете будет построено поле направлений в виде стрелок. Размер стрелок регулируется параметром arrows = SMALL , MEDIUM , LARGE , LINE или NONE .
Для того, чтобы нарисовать весь фазовый портрет, необходимо для каждой фазовой траектории указывать начальные условия: например, для системы двух дифференциальных уравнений первого порядка несколько начальных условий в команде DEplots указываются после задания диапазона изменения независимой переменной t : [[x(0)=x1, y(0)=y1], [x(0)=x2, y(0)=y2],…, [x(0)=xn, y(0)=yn]] .
Начальные условия можно задавать в более компактной форме: [t0, x0, y0] , где t0 — точка, в которой задаются начальные условия, x0 и y0 — значения искомых функций в точке t0 .
Фазовый протрет системы двух дифференциальных уравнений первого порядка можно также построить с помощью команды phaseportrait(sys, [x,y],x1..x2,[[cond]]) , где sys — система двух дифференциальных уравнений первого порядка, [x,y] — имена искомых функций, x1..x2 — интервал, на котором следует построить фазовый портрет, а в фигурных скобках указываются начальные условия. Эта команда находится в пакете DEtools , поэтому данный пакет должен быть предварительно загружен.
Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Задание 2.3.
1. Построить фазовый портрет системы дифференциальных уравнений:
для нескольких наборов начальных условий: х (0)=1, у (0)=0.2; х (0)=0, у (0)=1; х (0)=1, у (0)=0.4; х (0)=1, у (0)=0.75; х (0)=0, у (0)=1.5; х (0)= — 0.1, у (0)=0.7.
stepsize=0.1, arrows=none, linecolor=black);
2. Построить фазовый портрет с полем направлений автономной системы
для различных начальных условий х (0)=1, у (0)=0; х (0)= — 1, у (0)=0; х (0)= p , у (0)=1; х (0)= — p , у (0)=1; х (0)=3 p , у (0)=0.2; х (0)=3 p , у (0)=1; х (0)=3 p , у (0)=1.8; х (0)= — 2 p , у (0)=1;.
3. Построить фазовый портрет системы дифференциальных уравнений:
Начальные условия, диапазон изменения переменной и размеры координатных осей подбираются самостоятельно из соображений наглядности фазового портрета.
Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter
Видео:13. Как решить дифференциальное уравнение первого порядка?Скачать

10. Графическое представление решений дифференциальных уравнений
Графическое представление решений дифференциальных уравнений
Применение функции odeplot пакета plots
Для обычного графического представления результатов решения дифференциальных уравнений может использоваться функция odeplot из описанного выше пакета plots. Эта функция используется в следующем виде:
где s — запись (в выходной фирме) дифференциального уравнения или системы дифференциальных уравнений, решаемых численно функцией dsolve, vars — переменные, г — параметр, задающий пределы решения (например, а. .Ь), и о — необязательные дополнительные опции.
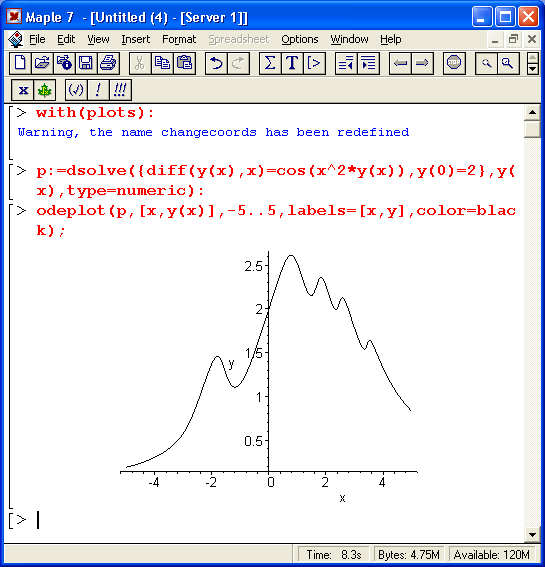
На рис. 13.5 представлен пример решения одиночного дифференциального уравнения с выводом решения у(х) с помощью функции odeplot.
В этом примере решается дифференциальное уравнение:
при у(0) = 2 и x, меняющемся от-5 до 5. Левая часть уравнения записана с помощью функции вычисления производной diff. Результатом построения является график решения у(х).
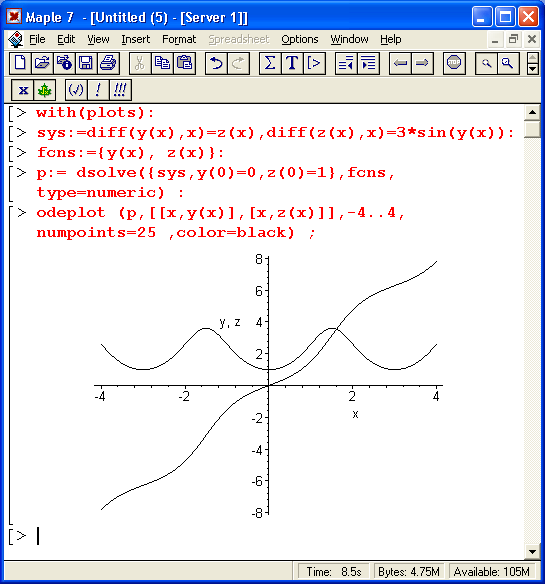
В другом примере (рис. 13.6) представлено решение системы из двух нелинейных дифференциальных уравнений. Здесь с помощью функции odeplot строятся графики двух функций. —у(х) и z(x).
В этом примере решается система:
при начальных условиях y(0)=0, z(0) = 1 их, меняющемся от -4 до 4 при числе точек решения, равном 25.
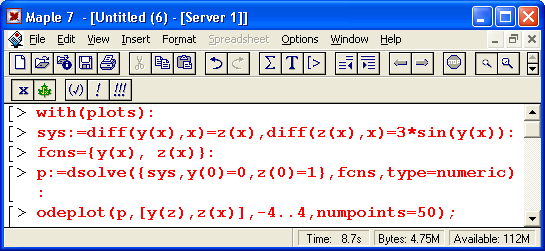
Иногда решение системы из двух дифференциальных уравнений (или одного дифференциального уравнения второго порядка) представляется в виде фазового портрета — при этом по осям графика откладываются значения у(х) и z(х) при изменении х в определенных пределах. Рисунок 13.7 демонстрирует построение фазового портрета для системы, представленной выше.
Обычное решение, как правило, более наглядно, чем фазовый портрет решения. Однако для специалистов (например, в теории колебаний) фазовый портрет порою дает больше информации, чем обычное решение. Он более трудоемок; для построения, поэтому возможность Марle 7 быстро строить фазовые портреты трудно переоценить.
Рис. 13.5. Пример решения одиночного дифференциального уравнения
Рис. 13.6. Пример решения системы из двух дифференциальных уравнений
Рис. 13.7. Представление решения системы дифференциальных уравнений в виде фазового портрета
Видео:Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

Построение графика функции методом дифференциального исчисления
Правила ввода функции
- Примеры
≡ x^2/(x+2)
cos 2 (2x+π) ≡ (cos(2*x+pi))^2≡ x+(x-1)^(2/3)
Пример №1 . Провести полное исследование функции 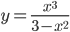
1) Функция определена всюду, кроме точек 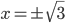
2) Функция нечетная, так как f(-x) = -f(x) , и, следовательно, ее график симметричен относительно начала координат. Поэтому ограничимся исследованием только для 0 ≤ x ≤ +∞.
3) Функция не периодическая.
4) Так как y=0 только при x=0, то пересечение с осями координат происходит только в начале координат.
5) Функция имеет разрыв второго рода в точке 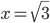
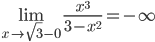
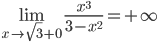
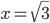
6) Находим 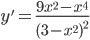
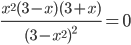
В окрестности точки x3=3 имеет: y’>0 при x 3, следовательно, в точке x3 функция имеет максимум, ymax(3)=-9/2. Найти первую производную функции
7) Находим 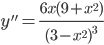

8) Выясним вопрос об асимптотах.
Наличие вертикальной асимптоты 

Найдем наклонные асимптоты: 

9) Теперь, используя полученные данные, строим чертеж:

Пример №2 . Построить график функции 
Решение.
1. Область определения функции D(y) = (-∞;0)U(0;∞).
2. Функция не является четной или нечетной.
3. Найдем точки пересечения графика с осью ОХ; имеем 

4. Точки разрыва x=0 , причем 
Найдем наклонные асимптоты: 

Наклонная асимптота имеет уравнение y=x .
5. Найдем экстремум функции и интервалы возрастания и убывания. Имеем 
6. Найдем интервалы выпуклости и вогнутости кривой и точки ее перегиба. Так как y’’>0 (x≠0), то график функции всюду вогнут. Точек перегиба кривая не имеет.
Строим график функции.
📺 Видео
Метод ЭйлераСкачать

Как в MATLAB Simulink моделировать уравнения (Структурная схема САУ)Скачать

Практика 1 ИзоклиныСкачать

MatLab. Решение дифференциального уравнения.Скачать

2. Дифференциальные уравнения с разделяющимися переменными. Часть 1.Скачать

Дифференциальные уравнения. 11 класс.Скачать

Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Решение системы дифференциальных уравнений методом ЭйлераСкачать

Решение физических задач с помощью дифференциальных уравненийСкачать

7. Линейные дифференциальные уравнения первого порядка. Метод Бернулли.Скачать

Геометрический смысл дифференциального уравненияСкачать

Линейное дифференциальное уравнение Коши-ЭйлераСкачать

Дифференциальные уравнения, 1 урок, Дифференциальные уравнения. Основные понятияСкачать














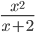 ≡ x^2/(x+2)
≡ x^2/(x+2) 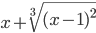 ≡ x+(x-1)^(2/3)
≡ x+(x-1)^(2/3)