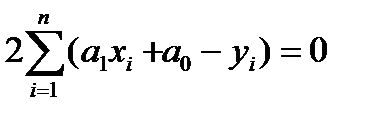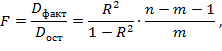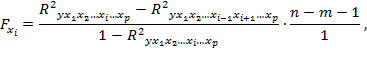Числитель в этой формуле может быть рассчитан через коэффициент детерминации и общую дисперсию признака-результата: 
Для параметра a критерий проверки гипотезы о незначимом отличии его от нуля имеет вид:

где 
μa – стандартная ошибка параметра a.
Для линейного парного уравнения регрессии: 
Для проверки гипотезы о незначимом отличии от нуля коэффициента линейной парной корреляции в генеральной совокупности используют следующий критерий: 
Для линейного парного уравнения регрессии: 
В парной линейной регрессии между наблюдаемыми значениями критериев существует взаимосвязь: t ( b =0) = t (r=0).
Пример №1 . Уравнение имеет вид y=ax+b
1. Параметры уравнения регрессии.
Средние значения
Связь между признаком Y фактором X сильная и прямая
Уравнение регрессии
Коэффициент детерминации
R 2 = 0.73 2 = 0.54, т.е. в 54% случаев изменения х приводят к изменению y . Другими словами — точность подбора уравнения регрессии — средняя.
| x | y | x 2 | y 2 | x ∙ y | y(x) | (y-y cp ) 2 | (y-y(x)) 2 | (x-x p ) 2 |
| 69 | 124 | 4761 | 15376 | 8556 | 128.48 | 491.36 | 20.11 | 367.36 |
| 83 | 133 | 6889 | 17689 | 11039 | 141.4 | 173.36 | 70.56 | 26.69 |
| 92 | 146 | 8464 | 21316 | 13432 | 149.7 | 0.03 | 13.71 | 14.69 |
| 97 | 153 | 9409 | 23409 | 14841 | 154.32 | 46.69 | 1.73 | 78.03 |
| 88 | 138 | 7744 | 19044 | 12144 | 146.01 | 66.69 | 64.21 | 0.03 |
| 93 | 159 | 8649 | 25281 | 14787 | 150.63 | 164.69 | 70.13 | 23.36 |
| 74 | 145 | 5476 | 21025 | 10730 | 133.1 | 1.36 | 141.68 | 200.69 |
| 79 | 152 | 6241 | 23104 | 12008 | 137.71 | 34.03 | 204.21 | 84.03 |
| 105 | 168 | 11025 | 28224 | 17640 | 161.7 | 476.69 | 39.74 | 283.36 |
| 99 | 154 | 9801 | 23716 | 15246 | 156.16 | 61.36 | 4.67 | 117.36 |
| 85 | 127 | 7225 | 16129 | 10795 | 143.25 | 367.36 | 263.91 | 10.03 |
| 94 | 155 | 8836 | 24025 | 14570 | 151.55 | 78.03 | 11.91 | 34.03 |
| 1058 | 1754 | 94520 | 258338 | 155788 | 1754 | 1961.67 | 906.57 | 1239.67 |
Значимость коэффициента корреляции
По таблице Стьюдента находим Tтабл
Tтабл (n-m-1;a) = (10;0.05) = 1.812
Поскольку Tнабл > Tтабл , то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициента корреляции статистически — значим.
Анализ точности определения оценок коэффициентов регрессии
S a = 0.2704
Доверительные интервалы для зависимой переменной
Рассчитаем границы интервала, в котором будет сосредоточено 95% возможных значений Y при неограниченно большом числе наблюдений и X = 88,16
(128.06;163.97)
Проверка гипотез относительно коэффициентов линейного уравнения регрессии
1) t-статистика
Статистическая значимость коэффициента регрессии a подтверждается (3.41>1.812).
Статистическая значимость коэффициента регрессии b подтверждается (2.7>1.812).
Доверительный интервал для коэффициентов уравнения регрессии
Определим доверительные интервалы коэффициентов регрессии, которые с надежность 95% будут следующими (tтабл=1.812):
(a — tтабл·S a; a + tтабл·Sa)
(0.4325;1.4126)
(b — tтабл·S b; b + tтабл·Sb)
(21.3389;108.3164)
2) F-статистики
Fkp = 4.96
Поскольку F > Fkp, то коэффициент детерминации статистически значим.
Пример №2 . По территориям региона приводятся данные за 199Х г.; <table х
1. Построить линейное уравнение парной регрессии у от х.
2. Рассчитать линейный коэффициент парной корреляции и среднюю ошибку аппроксимации.
3. Оценить статистическую значимость параметров регрессии и корреляции.
4. Выполнить прогноз заработной платы у при прогнозном значении среднедушевого прожиточного минимума х , составляющем 107% от среднего уровня.
5. Оценить точность прогноза, рассчитав ошибку прогноза и его доверительный интервал.
Решение находим с помощью калькулятора.
Использование графического метода .
Этот метод применяют для наглядного изображения формы связи между изучаемыми экономическими показателями. Для этого в прямоугольной системе координат строят график, по оси ординат откладывают индивидуальные значения результативного признака Y, а по оси абсцисс — индивидуальные значения факторного признака X.
Совокупность точек результативного и факторного признаков называется полем корреляции.
На основании поля корреляции можно выдвинуть гипотезу (для генеральной совокупности) о том, что связь между всеми возможными значениями X и Y носит линейный характер.
Линейное уравнение регрессии имеет вид y = bx + a + ε
Здесь ε — случайная ошибка (отклонение, возмущение).
Причины существования случайной ошибки:
1. Невключение в регрессионную модель значимых объясняющих переменных;
2. Агрегирование переменных. Например, функция суммарного потребления – это попытка общего выражения совокупности решений отдельных индивидов о расходах. Это лишь аппроксимация отдельных соотношений, которые имеют разные параметры.
3. Неправильное описание структуры модели;
4. Неправильная функциональная спецификация;
5. Ошибки измерения.
Так как отклонения εi для каждого конкретного наблюдения i – случайны и их значения в выборке неизвестны, то:
1) по наблюдениям xi и yi можно получить только оценки параметров α и β
2) Оценками параметров α и β регрессионной модели являются соответственно величины а и b, которые носят случайный характер, т.к. соответствуют случайной выборке;
Тогда оценочное уравнение регрессии (построенное по выборочным данным) будет иметь вид y = bx + a + ε, где ei – наблюдаемые значения (оценки) ошибок εi, а и b соответственно оценки параметров α и β регрессионной модели, которые следует найти.
Для оценки параметров α и β — используют МНК (метод наименьших квадратов).
Система нормальных уравнений.
Для наших данных система уравнений имеет вид
12a+1027b=1869
1027a+89907b=161808
Из первого уравнения выражаем а и подставим во второе уравнение. Получаем b = 0.92, a = 76.98
Уравнение регрессии: y = 0.92 x + 76.98
1. Параметры уравнения регрессии.
Выборочные средние.
Коэффициент корреляции
Рассчитываем показатель тесноты связи. Таким показателем является выборочный линейный коэффициент корреляции, который рассчитывается по формуле:
Линейный коэффициент корреляции принимает значения от –1 до +1.
Связи между признаками могут быть слабыми и сильными (тесными). Их критерии оцениваются по шкале Чеддока:
0.1 0 – прямая связь, иначе — обратная). В нашем примере связь прямая.
Коэффициент эластичности.
Коэффициенты регрессии (в примере b) нежелательно использовать для непосредственной оценки влияния факторов на результативный признак в том случае, если существует различие единиц измерения результативного показателя у и факторного признака х.
Для этих целей вычисляются коэффициенты эластичности и бета — коэффициенты. Коэффициент эластичности находится по формуле:
Он показывает, на сколько процентов в среднем изменяется результативный признак у при изменении факторного признака х на 1%. Он не учитывает степень колеблемости факторов.
Коэффициент эластичности меньше 1. Следовательно, при изменении среднедушевого прожиточного минимума в день на 1%, среднедневная заработная плата изменится менее чем на 1%. Другими словами — влияние среднедушевого прожиточного минимума Х на среднедневную заработную плату Y не существенно.
Бета – коэффициент показывает, на какую часть величины своего среднего квадратичного отклонения изменится в среднем значение результативного признака при изменении факторного признака на величину его среднеквадратического отклонения при фиксированном на постоянном уровне значении остальных независимых переменных:
Т.е. увеличение x на величину среднеквадратического отклонения этого показателя приведет к увеличению средней среднедневной заработной платы Y на 0.721 среднеквадратичного отклонения этого показателя.
1.4. Ошибка аппроксимации.
Оценим качество уравнения регрессии с помощью ошибки абсолютной аппроксимации.
Поскольку ошибка меньше 15%, то данное уравнение можно использовать в качестве регрессии.
Коэффициент детерминации.
Квадрат (множественного) коэффициента корреляции называется коэффициентом детерминации, который показывает долю вариации результативного признака, объясненную вариацией факторного признака.
Чаще всего, давая интерпретацию коэффициента детерминации, его выражают в процентах.
R 2 = 0.72 2 = 0.5199, т.е. в 51.99 % случаев изменения среднедушевого прожиточного минимума х приводят к изменению среднедневной заработной платы y. Другими словами — точность подбора уравнения регрессии — средняя. Остальные 48.01% изменения среднедневной заработной платы Y объясняются факторами, не учтенными в модели. <table 2
2.1. Значимость коэффициента корреляции.
По таблице Стьюдента с уровнем значимости α=0.05 и степенями свободы k=10 находим tкрит:
tкрит = (10;0.05) = 1.812
где m = 1 — количество объясняющих переменных.
Если tнабл > tкритич, то полученное значение коэффициента корреляции признается значимым (нулевая гипотеза, утверждающая равенство нулю коэффициента корреляции, отвергается).
Поскольку tнабл > tкрит, то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициент корреляции статистически — значим.
В парной линейной регрессии t 2 r = t 2 b и тогда проверка гипотез о значимости коэффициентов регрессии и корреляции равносильна проверке гипотезы о существенности линейного уравнения регрессии.
2.3. Анализ точности определения оценок коэффициентов регрессии.
Несмещенной оценкой дисперсии возмущений является величина:
S 2 y = 157.4922 — необъясненная дисперсия (мера разброса зависимой переменной вокруг линии регрессии).
12.5496 — стандартная ошибка оценки (стандартная ошибка регрессии).
S a — стандартное отклонение случайной величины a.
Sb — стандартное отклонение случайной величины b.
2.4. Доверительные интервалы для зависимой переменной.
Экономическое прогнозирование на основе построенной модели предполагает, что сохраняются ранее существовавшие взаимосвязи переменных и на период упреждения.
Для прогнозирования зависимой переменной результативного признака необходимо знать прогнозные значения всех входящих в модель факторов.
Прогнозные значения факторов подставляют в модель и получают точечные прогнозные оценки изучаемого показателя.
(a + bxp ± ε)
где
Рассчитаем границы интервала, в котором будет сосредоточено 95% возможных значений Y при неограниченно большом числе наблюдений и X p = 94
(76.98 + 0.92*94 ± 7.8288)
(155.67;171.33)
С вероятностью 95% можно гарантировать, что значения Y при неограниченно большом числе наблюдений не выйдет за пределы найденных интервалов.
2.5. Проверка гипотез относительно коэффициентов линейного уравнения регрессии.
1) t-статистика. Критерий Стьюдента.
Проверим гипотезу H0 о равенстве отдельных коэффициентов регрессии нулю (при альтернативе H1 не равно) на уровне значимости α=0.05.
tкрит = (10;0.05) = 1.812
Поскольку 3.2906 > 1.812, то статистическая значимость коэффициента регрессии b подтверждается (отвергаем гипотезу о равенстве нулю этого коэффициента).
Поскольку 3.1793 > 1.812, то статистическая значимость коэффициента регрессии a подтверждается (отвергаем гипотезу о равенстве нулю этого коэффициента).
Доверительный интервал для коэффициентов уравнения регрессии.
Определим доверительные интервалы коэффициентов регрессии, которые с надежность 95% будут следующими:
(b — tкрит Sb; b + tкрит Sb)
(0.9204 — 1.812·0.2797; 0.9204 + 1.812·0.2797)
(0.4136;1.4273)
С вероятностью 95% можно утверждать, что значение данного параметра будут лежать в найденном интервале.
(a-ta)
(76.9765 — 1.812·24.2116; 76.9765 + 1.812·24.2116)
(33.1051;120.8478)
С вероятностью 95% можно утверждать, что значение данного параметра будут лежать в найденном интервале.
2) F-статистики. Критерий Фишера.
Проверка значимости модели регрессии проводится с использованием F-критерия Фишера, расчетное значение которого находится как отношение дисперсии исходного ряда наблюдений изучаемого показателя и несмещенной оценки дисперсии остаточной последовательности для данной модели.
Если расчетное значение с k1=(m) и k2=(n-m-1) степенями свободы больше табличного при заданном уровне значимости, то модель считается значимой.
где m – число факторов в модели.
Оценка статистической значимости парной линейной регрессии производится по следующему алгоритму:
1. Выдвигается нулевая гипотеза о том, что уравнение в целом статистически незначимо: H0: R 2 =0 на уровне значимости α.
2. Далее определяют фактическое значение F-критерия:
где m=1 для парной регрессии.
3. Табличное значение определяется по таблицам распределения Фишера для заданного уровня значимости, принимая во внимание, что число степеней свободы для общей суммы квадратов (большей дисперсии) равно 1 и число степеней свободы остаточной суммы квадратов (меньшей дисперсии) при линейной регрессии равно n-2.
4. Если фактическое значение F-критерия меньше табличного, то говорят, что нет основания отклонять нулевую гипотезу.
В противном случае, нулевая гипотеза отклоняется и с вероятностью (1-α) принимается альтернативная гипотеза о статистической значимости уравнения в целом.
Табличное значение критерия со степенями свободы k1=1 и k2=10, Fkp = 4.96
Поскольку фактическое значение F > Fkp, то коэффициент детерминации статистически значим (Найденная оценка уравнения регрессии статистически надежна).
Видео:Коэффициент корреляции. Статистическая значимостьСкачать

Лекция 7. Парная регрессия. Оценка статистической значимости параметров уравнения и модели в целом.
ТЕМА 4. СТАТИСТИЧЕСКИЕ МЕТОДЫ ИЗУЧЕНИЯ СВЯЗЕЙ
Уравнение регрессии —этоаналитическое представление корреляционной зависимости. Уравнение регрессии описывает гипотетическую функциональную зависимость между условным средним значением результативного признака и значением признака – фактора (факторов), т.е. основную тенденцию зависимости.
Парная корреляционная зависимость описывается уравнением парной регрессии, множественная корреляционная зависимость – уравнением множественной регрессии.
Признак-результат в уравнении регрессии – это зависимая переменная (отклик, объясняемая переменная), а признак-фактор – независимая переменная (аргумент, объясняющая переменная).
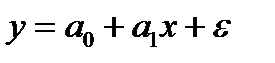
где y – зависимая переменная (признак-результат); x – независимая переменная (признак-фактор); 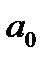

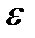
В качестве уравнения регрессии могут быть использованы различные математические функции. Частое практическое применение находят уравнения линейной зависимости, параболы, гиперболы, степной функции и др.
Как правило, анализ начинается с оценки линейной зависимости, поскольку результаты легко поддаются содержательной интерпретации. Выбор типа уравнения связи – достаточно ответственный этап анализа. В «докомпьютерную» эпоху эта процедура была сопряжена с определенными сложностями и требовала от аналитика знания свойств математических функций. В настоящее время на базе специализированных программ можно оперативно построить множество уравнений связи и на основе формальных критериев осуществить выбор лучшей модели (однако математическая грамотность аналитика не утратила своей актуальности).
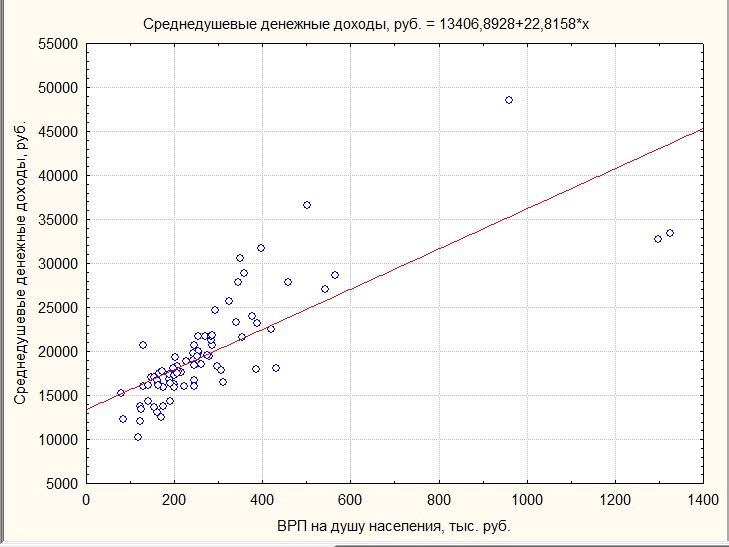
Гипотезу о типе корреляционной зависимости можно выдвинуть по результатам построения поля корреляции (см. лекцию 6). Исходя из характера расположения точек на графике (координаты точек соответствуют значениям зависимой и независимой переменных), выявляется тенденция связи между признаками (показателями). Если линия регрессии проходит через все точки поля корреляции, то эта свидетельствует о функциональной связи. В практике социально-экономических исследований такую картину наблюдать не приходится, поскольку присутствует статистическая (корреляционная) зависимость. В условиях корреляционной зависимости при нанесении линии регрессии на диаграмму рассеивания наблюдается отклонение точек поля корреляции от линии регрессии, что демонстрирует, так называемые, остатки или ошибки оценивания (см. рисунок 7.1).
Наличие ошибки уравнения связано с тем, что:
§ не все факторы, влияющие на результат, учитываются в уравнении регрессии;
§ может быть неверно выбранаформа связи — уравнение регрессии;
§ не все факторы включены в уравнение.
Построить уравнение регрессии – означает рассчитать значения его параметров. Уравнение регрессии строится на основе фактических значений анализируемых признаков. Расчет параметров, как правило, выполняется с использованием метода наименьших квадратов (МНК).
Суть МНКсостоит в том, что удается получить такие значения параметров уравнения, при которых минимизируется сумма квадратов отклонений теоретических значений признака-результата (рассчитанных на основе уравнения регрессии), от фактических его значений:
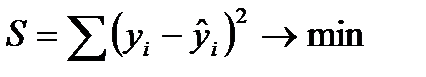
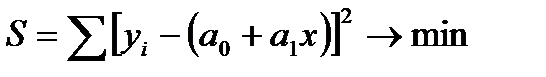

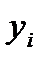
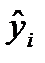
Т.о., решается задача на экстремум, то есть необходимо найти, при каких значениях параметров, функция S достигает минимума.
Проводя дифференцирование, приравнивая частные производные нулю:
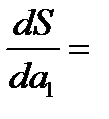

и далее, решая систему нормальных уравнений, находят значения параметров 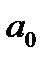

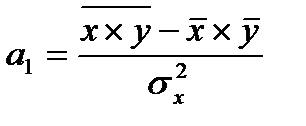

где 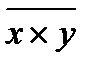
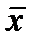
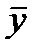
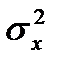
Параметр 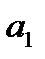
В рамках рассматриваемого примера, в программе STATISTICA рассчитаны параметры уравнения регрессии, описывающего зависимость между уровнем среднедушевых денежных доходов населения и величиной валового регионального продукта на душу населения в регионах России, см. таблицу 7.1.
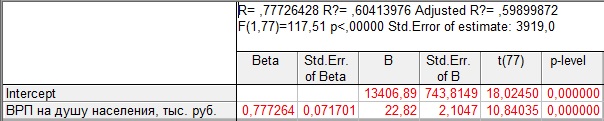
Таблица 7.1 — Расчет и оценка параметров уравнения, описывающего зависимостьмежду уровнем среднедушевых денежных доходов населения и величиной валового регионального продукта на душу населения в регионах России, 2013 г.
В графе «В» таблицы содержатся значения параметров уравнения парной регрессии, следовательно, можно записать: 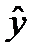
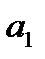
Параметр 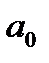
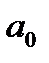
Рисунок 7.1 — Поле корреляции и линия регрессии, отражающие зависимость уровня среднедушевых денежных доходов населения в регионах России и величины ВРП на душу населения
Значение параметра 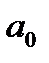
Построение уравнения регрессии сопровождается оценкой статистической значимости уравнения в целом и его параметров. Необходимость таких процедур связана с ограниченным объемом данных, что может препятствовать действию закона больших чисел и, следовательно, выявлению истинной тенденции во взаимосвязи анализируемых показателей. Кроме того, любую исследуемую совокупность можно рассматривать как выборку из генеральной совокупности, а характеристики, полученные в ходе анализа, как оценку генеральных параметров.
Оценка статистической значимости параметров и уравнения в целом – это обоснование возможности использования построенной модели связи для принятия управленческих решений и прогнозирования (моделирования).
Статистическая значимость уравнения регрессиив целом оценивается с использованием F-критерия Фишера, который представляет собой отношение факторной и остаточных дисперсий, рассчитанных на одну степень свободы:
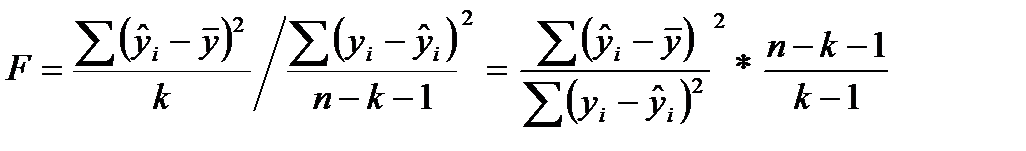
где 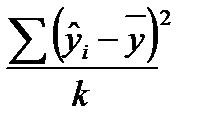
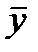
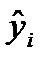
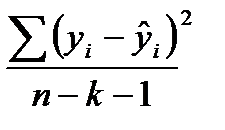
Величина F-критерия Фишера, согласно формуле, характеризует соотношение между факторной и остаточной дисперсиями зависимой переменной, демонстрируя, по существу, во сколько раз величина объясненной части вариации превышает необъясненную.
F-критерий Фишера табулирован, входом в таблицу является число степеней свободы факторной и остаточной дисперсий. Сравнение расчетного значения критерия с табличным (критическим) позволяет ответить на вопрос: статистически значима ли та часть вариации признака-результата, которую удается объяснить факторами, включенными в уравнение данного вида. Если 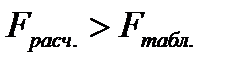
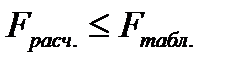
Оценка статистической значимости параметров уравнения осуществляется на основе t-статистики, которая рассчитывается как отношение модуля параметров уравнения регрессии к их стандартным ошибкам ( 
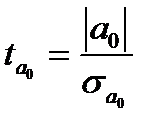
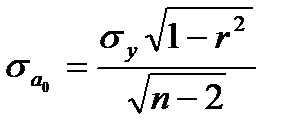
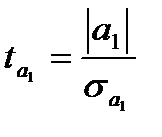
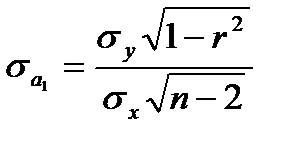
где 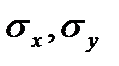
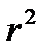
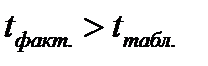
Оценка параметров на основе t-статистики, по существу, является проверкой нулевой гипотезы о равенстве генеральных параметров нулю (H0: 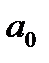
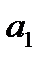

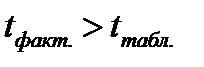

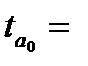

Для оценки статистической значимости уравнения в целом обратимся к значению F-критерия Фишера (см. таблицу 7.1). Расчетное значение F-критерия = 117,51, табличное значение критерия, исходя из соответствующего числа степеней свободы (для факторной дисперсии d.f. =1, для остаточной дисперсииd.f. =77), равно 4,00 (см. приложение. ). Таким образом, 
Проводя оценку статистической значимости уравнения регрессии и его параметров, можем получить различное сочетание результатов.
· Уравнение по F-критерию статистически значимо и все параметры уравнения по t-статистике тоже статистически значимы. Данное уравнение может быть использовано как для принятия управленческих решений (на какие факторы следует воздействовать, чтобы получить желаемый результат), так и для прогнозирования поведения признака-результата при тех или иных значениях факторов.
· По F-критерию уравнение статистически значимо, но незначимы параметры (параметр) уравнения. Уравнение может быть использовано для принятия управленческих решений (касающихся тех факторов, по которым получено подтверждение статистической значимости их влияния), но уравнение не может быть использовано для прогнозирования.
· Уравнение по F-критерию статистически незначимо. Уравнение не может быть использовано. Следует продолжить поиск значимых признаков-факторов или аналитической формы связи аргумента и отклика.
Если подтверждена статистическая значимость уравнения и его параметров, то может быть реализован, так называемый, точечный прогноз, т.е. получена оценка значения признака-результата (y) при тех или иных значениях фактора (x).
Совершенно очевидно, что прогнозное значение зависимой переменной, рассчитанное на основе уравнения связи, не будет совпадать с фактическим ее значением ( 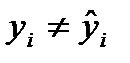
Разность между фактическими и теоретическими значениями зависимой переменной называют отклонениями или ошибками, или остатками. На основе этих величин рассчитывается остаточная дисперсия. Квадратный корень из остаточной дисперсии и является среднеквадратической (стандартной) ошибкой оценивания:
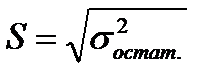
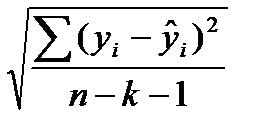
Стандартная ошибка уравнения измеряется в тех же единицах, что и прогнозируемый показатель. Если ошибки уравнения подчиняются нормальному распределению (при больших объемах данных), то 95 процентов значений должны находиться от линии регрессии на расстоянии, не превышающем 2S (исходя из свойства нормального распределения — правила трех сигм). Величина стандартной ошибки оценивания используется при расчете доверительных интервалов при прогнозировании значения признака — результата для конкретной единицы совокупности.
В практических исследованиях часто возникает необходимость в прогнозе среднего значения признака — результата при том или ином значении признака — фактора. В этом случае в расчете доверительного интервала для среднего значения зависимой переменной( 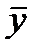
учитывается величина средней ошибки:
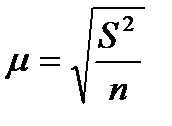
Использование разных величин ошибок объясняется тем, что изменчивость уровней показателей у конкретных единиц совокупности гораздо выше, чем изменчивость среднего значения, следовательно, ошибка прогноза среднего значения меньше.
Доверительный интервал прогноза среднего значения зависимой переменной:
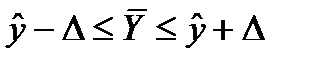
где 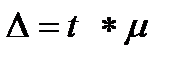
Доверительный интервал для прогнозируемого значения признака-результата может быть рассчитан и с учетом поправки на смещение (сдвиг) линии регрессии. Величина поправочного коэффициента определяется:
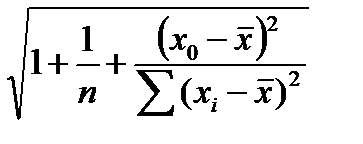
где 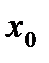

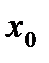
На точность прогноза на основе уравнения регрессии могут влиять разные причины. Прежде всего, следует учитывать, что оценка качества уравнения и его параметров проводится, исходя из предположения о нормальном распределении случайных остатков. Нарушение этого допущения может быть связано с наличием резко отличающихся значений в данных, с неравномерной вариацией, с наличием нелинейной зависимости. В этом случае качество прогноза снижается. Второй момент, о котором следует помнить, — значения факторов, учитываемые при прогнозировании результата, не должны выходить за пределы размаха вариации данных, на основе которых построено уравнение.
Видео:Эконометрика. Оценка значимости параметров уравнения регрессии. Критерий Стьюдента.Скачать

Оценка значимости уравнения множественной регрессии
Построение эмпирического уравнения регрессии является начальным этапом эконометрического анализа. Первое же построенное по выборке уравнение регрессии очень редко является удовлетворительным по тем или иным характеристикам. Поэтому следующей важнейшей задачей эконометрического анализа является проверка качества уравнения регрессии. В эконометрике принята устоявшаяся схема такой проверки.
Итак, проверка статистического качества оцененного уравнения регрессии проводится по следующим направлениям:
· проверка значимости уравнения регрессии;
· проверка статистической значимости коэффициентов уравнения регрессии;
· проверка свойств данных, выполнимость которых предполагалась при оценивании уравнения (проверка выполнимости предпосылок МНК).
Проверка значимости уравнения множественной регрессии, так же как и парной регрессии, осуществляется с помощью критерия Фишера. В данном случае (в отличие от парной регрессии) выдвигается нулевая гипотеза Н0 о том, что все коэффициенты регрессии равны нулю (b1=0, b2=0, … , bm=0). Критерий Фишера определяется по следующей формуле:
где Dфакт — факторная дисперсия, объясненная регрессией, на одну степень свободы; Dост— остаточная дисперсия на одну степень свободы; R 2 — коэффициент множественной детерминации; т — число параметров при факторах х в уравнении регрессии (в парной линейной регрессии т = 1); п — число наблюдений.
Полученное значение F-критерия сравнивается с табличным при определенном уровне значимости. Если его фактическое значение больше табличного, тогда гипотеза Но о незначимости уравнения регрессии отвергается, и принимается альтернативная гипотеза о его статистической значимости.
С помощью критерия Фишера можно оценить значимость не только уравнения регрессии в целом, но и значимость дополнительного включения в модель каждого фактора. Такая оценка необходима для того, чтобы не загружать модель факторами, не оказывающими существенного влияния на результат. Кроме того, поскольку модель состоит из несколько факторов, то они могут вводиться в нее в различной последовательности, а так как между факторами существует корреляция, значимость включения в модель одного и того же фактора может различаться в зависимости от последовательности введения в нее факторов.
Для оценки значимости включения дополнительного фактора в модель рассчитывается частный критерий Фишера Fxi. Он построен на сравнении прироста факторной дисперсии, обусловленного включением в модель дополнительного фактора, с остаточной дисперсией на одну степень свободы по регрессии в целом. Следовательно, формула расчета частного F-критерия для фактора будет иметь следующий вид:
где R 2 yx1x2…xi…xp — коэффициент множественной детерминации для модели с полным набором п факторов; R 2 yx1x2…x i-1 x i+1…xp — коэффициент множественной детерминации для модели, не включающей фактор xi; п — число наблюдений; т — число параметров при факторах x в уравнении регрессии.
Фактическое значение частного критерия Фишера сравнивается с табличным при уровне значимости 0,05 или 0,1 и соответствующих числах степеней свободы. Если фактическое значение Fxi превышает Fтабл , то дополнительное включение фактора xi в модель статистически оправдано, и коэффициент «чистой» регрессии bi при факторе xi статистически значим. Если же Fxi меньше Fтабл , то дополнительное включение в модель фактора существенно не увеличивает долю объясненной вариации результата у, и, следовательно, его включение в модель не имеет смысла, коэффициент регрессии при данном факторе в этом случае статистически незначим.
С помощью частного критерия Фишера можно проверить значимость всех коэффициентов регрессии в предположении, что каждый соответствующий фактор xi вводится в уравнение множественной регрессии последним, а все остальные факторы были уже включены в модель раньше.
Оценка значимости коэффициентов «чистой» регрессии bi по критерию Стьюдента t может быть проведена и без расчета частных F-критериев. В этом случае, как и при парной регрессии, для каждого фактора применяется формула
где bi — коэффициент «чистой» регрессии при факторе xi ; mbi — стандартная ошибка коэффициента регрессии bi .
Для множественной линейной регрессии стандартная ошибка коэффициента регрессии рассчитывается по следующей формуле:
где σy , σxi — среднее квадратическое отклонение соответственно для результата у и xi ; R 2 yx1x2…xi…xp — коэффициент множественной детерминации для множественной регрессии с набором из р факторов; R 2 xi x1x2…x i-1 x i+1…xp — коэффициент детерминации для зависимости фактора xi с остальными факторами множественной регрессии.
Полученные значения t-критериев сравниваются с табличными, и на основе этого сравнения принимается или отвергается гипотеза о значимости каждого коэффициента регрессии в отдельности.
Дата добавления: 2015-10-05 ; просмотров: 5711 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
🔥 Видео
Эконометрика. Оценка значимости уравнения регрессии. Критерий ФишераСкачать

Что такое значение p? /Простая статистика/Скачать

Критерий Фишера для проверки адекватности построенной регрессииСкачать

Корреляционно-регрессионный анализ многомерных данных в ExcelСкачать

Что такое статистическая значимость. Теория вероятностей.Скачать

Самое понятное объяснение p-valueСкачать

Математическое Ожидание, Дисперсия, Стандартное Отклонение за 5 минутСкачать

Непараметрические методы оценки статистической значимостиСкачать

Множественная регрессияСкачать

Т-критерий Стьюдента за 12 минут. Биостатистика.Скачать

Метод наименьших квадратов. Парная регрессия расчет без Excel @economc #МНК #регрессия #корреляцияСкачать

t-критерий Стьюдента для проверки гипотезы о средней в MS ExcelСкачать
Эконометрика. Линейная парная регрессияСкачать

Расчет коэффициента корреляции в ExcelСкачать

Пример проверки гипотезы о незначимости регрессииСкачать

Статистический метод (критерий): как выбрать для анализа?Скачать

11 класс, 24 урок, Статистические методы обработки информацииСкачать

Ключевые моменты методики регрессионного анализаСкачать