Рассмотрим уравнение Фредгольма второго рода
Дадим определение: ядро интегрального уравнения называется вырожденным , если его можно представить в виде конечной суммы произведений двух функций, из которых одна зависит только от t, а другая только от s:
Будем считать, что функции между собой линейно независимы.
Предположим , что непрерывны на отрезке [a, b], тогда ядро будет непрерывным в прямоугольнике Q .
Рассмотрим интегральное уравнение Фредгольма 2-го рода с вырожденным ядром :
где f(t)- непрерывная на отрезке [a, b] функция.
Пусть уравнение (2) имеет решение Положим
Тогда из (2) получим
Отсюда видно, что решение этого интегрального уравнения с вырожденным ядром сводится к определению постоянных . заменив в равенстве (4) индекс суммирования I на j, умножим обе части этого равенства на и проинтегрируем по t в пределах a до b:
Видео:Интегральные уравнения с вырожденным ядромСкачать
получим систему алгебраических уравнений, которой должны удовлетворять коэффициенты :
Если эта система неразрешима, то, очевидно, интегральное уравнение (2) также неразрешимо.
Предположим что система (6) имеет решение подставив эти значения коэффициентов в формулу (4) получим функцию , которая является решением интегрального уравнения (2), в этом можно убедиться сделав проверку.
Таким образом, интегральное уравнение (2) и система линейных алгебраических уравнений (6) эквивалентны в том смысле, что разрешимость системы (6) влечет за собой разрешимость уравнения (2) и наоборот.
Определитель системы (6) D(л) равен
— многочлен относительно л степени не выше n , отличный от тождественного нуля, так как
Следовательно, имеет не более n различных корней.
называют определителем Фредгольма для интегрального уравнения (2), а его нули, т.е корни уравнения , называют характеристическими числами ядра или уравнение (2)
Рассмотрим некоторые Теоремы Фредгольма:
I. Если л не является характеристическим числом, то интегральное уравнение (2) имеет единственное решение , определяемое формулой (4), при любом свободном члене f(t).
В случае когда Соответствующее однородное интегральное уравнения
Видео:Интегральные уравнения Фредгольма второго рода Случай вырожденного ядра Неоднородный случайСкачать
отвечающее условию , имеет только тривиальное решение . В самом деле если то все равны нулю и система (6) будет системой однородных линейных уравнений с определителем, отличных от нуля. Такая система имеет только нулевое решение . Поэтому первую теорему Фредгольма иногда формулируют так:
для того чтобы уравнение (2) имело единственное решение при любой функции f(t) , необходимо и достаточно, чтобы соответствующее однородное уравнение имело только тривиальное решение .
II. Рассмотрим другой случай, пусть теперь совпадает с одним из нулей определителя Фредгольма , т.е является характеристическим числом ядра
Тогда определитель системы (6) будет равен нулю. Соответствующая однородная система
имеет при этом некоторое число p линейно независимых ненулевых вектор-решений
Будут нетривиальными решениями соответствующего однородного интегрального уравнения
Нетривиальные решения однородного уравнения называются собственными или фундаментальными функциями этого уравнения или ядра K(t,s). Число линейно независимых функций , соответствующее данному характеристическому числу, называется его рангом или кратностью.
Если же — собственные функции, отвечающие одному и тому же характеристическому числу л, то их сумма будет также собственной функцией , отвечающей этому же числу л. Точно так же, если — собственная функция, то — любая постоянная, будет собственной функцией ядра K(t,s).
Общим решением однородного уравнения (15), отвечающие данному характеристическому числу л, будет функция
Где произвольные постоянные.
Введем некоторые понятия. имеем интегральное уравнение Фредгольма
Видео:Интегральные уравнения Фредгольма второго рода Случай вырожденного ядря Однородный случайСкачать
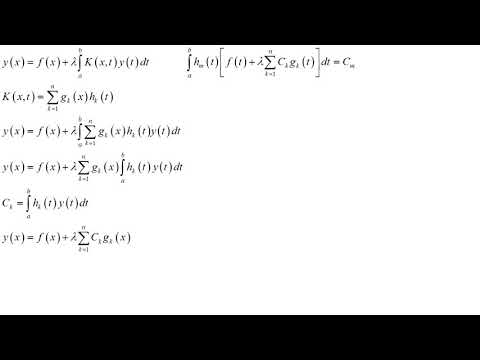
Дадим определение: ядро , получаемое из ядра заменой t на s и наоборот, называется сопряженным с ядром K(t,s): (21)
В случае, когда есть комплекснозначная функция действительных аргументов t,s полагаем по определению
где означает величину, комплексно сопряженную с .
называется сопряженным с уравнением (20)
для интегрального уравнения (2) с вырожденным ядром сопряженное с ним уравнение имеет вид
Если , т.е уравнение (23) однородное , то для определения получаем однородную систему
Сопряженную с системой (13).
В силу теоремы 1 обе эти системы имеют одинаковое число p линейно независимых вектор-решений.
Если ненулевые вектор-решения системы (26), то функции
будут собственными функциями однородного уравнения
сопряженного с уравнением (9).
Видео:Метод определителей ФредгольмаСкачать
Итак, если есть характеристическое число ядра , то однородное интегральное уравнение (15) и сопряженное с ним уравнение (27) имеют одно и то же конечное число линейно независимых собственных функций. алгебраический уравнение интегральный колебание
Это — вторая теорема Фредгольма.
III. Рассмотрим, наконец, неоднородное уравнение (2) в случае, когда -характеристическое число.
Как мы отмечали , его разрешимость эквивалентна разрешимости неоднородной системы (6) линейных алгебраических уравнений
Воспользуемся теоремой: для того чтобы неоднородная система линейных алгебраических уравнений была разрешима, необходимо и достаточно, чтобы вектор свободных членов этой системы был ортогонален ко всем вектор-решениям сопряженной однородной системы.
Согласно этой теореме, неоднородная система(6) будет разрешима тогда и только тогда, когда вектор будет ортогонален каждому из векторов , т.е когда
Но , и, следовательно, условие (28) можно записать так:
Таким образом, сформулируем третью теорему Фредгольма: неоднородное интегральное уравнение (2) с вырожденным ядром при характеристическом значении будет разрешимо тогда и только тогда, когда свободный член f(t) будет ортогонален ко всем решениям сопряженного однородного интегрального уравнения (27).
Подчеркнем, что вопрос о разрешимости уравнения (2) требует проверки конечного числа p условий
Если эти условия выполнены, то уравнение (2) имеет бесчисленное множество решений. Все они описываются формулой
где — какое либо решение неоднородного уравнения (2), а — общее решение соответствующего однородногоуравнени.
Видео:Уравнения Фредгольма - 2Скачать
Как следствие из предыдущих теорем вытекает важная теорема об альтернативе: если однородное интегральное уравнение Фредгольма с вырожденным ядром имеет только тривиальное решение, то соответствующее неоднородное уравнение всегда имеет одно и только одно решение. Если же однородное уравнение имеет нетривиальное решение, то неоднородное интегральное уравнение в зависимости от свободного члена f(t) либо вовсе не имеет решения, либо имеет бесконечное число решений.
💥 Видео
Интегральное уравнение Вольтерра второго рода Пример решения методом разрешающего ядраСкачать
Интегральные уравнения Вольтерра второго рода Метод разрешающего ядра или Метод резольвентыСкачать
Метод итерированных ядерСкачать
Интегральные уравнения Вольтерра второго рода Операционный метод для случаев разностного ядраСкачать
Интегральные уравнения Вольтерра второго рода Метод последовательных приближенийСкачать
Методы численного анализа - Уравнения Фредгольма и ВольтерраСкачать
Уравнения Фредгольма - 1Скачать
Курс по ИДУ: Интегральные уравнения Фредгольма с вырожденным ядром | Занятие 7Скачать
Ягола А. Г. - Интегральные уравнения - Уравнение Фредгольма 2-го рода с непрерывными ядрамиСкачать
Курс по ИДУ: Методы решения интегральных уравнений Вольтерра и Фредгольма | Занятие 6Скачать
Метод решения интегрального уравнения Вольтерра второго рода с помощью резольвентыСкачать
Уравнения Вольтерра - 1Скачать
Интегральные уравнения ВольтерраСкачать
