Как отмечать точки на графике уравнения

Видео:Линейная функция: краткие ответы на важные вопросы | Математика | TutorOnlineСкачать

Построение графиков функций

О чем эта статья:

11 класс, ЕГЭ/ОГЭ

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Видео:Точки пересечения графика линейной функции с координатными осями. 7 класс.Скачать

Понятие функции

Функция — это зависимость y от x, где x является переменной или аргументом функции, а y — зависимой переменной или значением функции.

Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:

• Табличный способ — помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
• Графический способ — наглядно.
• Аналитический способ — через формулы. Компактно, и можно посчитать функцию при произвольном значении аргумента из области определения.
• Словесный способ.

Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.

Например, для функции вида область определения выглядит так

• х ≠ 0, потому что на ноль делить нельзя. Записать можно так: D (y): х ≠ 0.

Область значений — множество у, то есть это значения, которые может принимать функция.

Например, естественная область значений функции y = x² — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.

Видео:Построить график ЛИНЕЙНОЙ функции и найти:Скачать

Понятие графика функции

Графиком функции y = f(x) называется множество точек (x; y), координаты которых связаны соотношением y = f(x). Само равенство y = f(x) называется уравнением данного графика.

График функции — это множество точек (x; y), где x — это аргумент, а y — значение функции, которое соответствует данному аргументу.

Проще говоря, график функции показывает множество всех точек, координаты которых можно найти, просто подставив в функцию любые числа вместо x.

Для примера возьмём самую простую функцию, в которой аргумент равен значению функции, то есть y = x.

В этом случае нам не придётся вычислять для каждого аргумента значение функции, так как они равны, поэтому у всех точек нашего графика абсцисса будет равна ординате.

Отметим любые три точки на координатной плоскости, например: L (-2; -2), M (0; 0) и N (1; 1).

Если мы последовательно от наименьшего значения аргумента к большему соединим отмеченные точки, то у нас получится прямая линия. Значит графиком функции y = x является прямая. На графике это выглядит так:

Надпись на чертеже y = x — это уравнение графика. Ставить надпись с уравнением на чертеже удобно, чтобы не запутаться в решении задач.

Важно отметить, что прямая линия бесконечна в обе стороны. Хоть мы и называем часть прямой графиком функции, на самом деле на чертеже изображена только малая часть графика.

Видео:Определить, принадлежит ли точка с заданными координатами графику функцииСкачать

Исследование функции

Важные точки графика функции y = f(x):

• стационарные и критические точки;
• точки экстремума;
• нули функции;
• точки разрыва функции.

Стационарные точки — точки, в которых производная функции f(x) равна нулю.

Критические точки — точки, в которых производная функции f(x) равна нулю либо не существует. Стационарные точки являются подмножеством множества критических точек.

Экстремум в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума.

Нули функции — это значения аргумента, при которых функция равна нулю.

Асимптота — прямая, которая обладает таким свойством, что расстояние от точки графика функции до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат. По способам их отыскания выделяют три вида асимптот: вертикальные, горизонтальные, наклонные.

Функция непрерывна в точке k, если предел функции в данной точке равен значению функции в этой точке:

Если функция f(x) не является непрерывной в точке x = a, то говорят, что f(x) имеет разрыв в этой точке.

Если нам нужно построить график незнакомой функции, когда заранее невозможно представить вид графика, полезно применять схему исследования свойств функции. Она поможет составить представление о графике и приступить к построению по точкам.

Схема построения графика функции:

1. Найти область определения функции.
2. Найти область допустимых значений функции.
3. Проверить не является ли функция четной или нечетной.
4. Проверить не является ли функция периодической.
5. Найти нули функции.
6. Найти промежутки знакопостоянства функции, то есть промежутки, на которых она строго положительна или строго отрицательна.
7. Найти асимптоты графика функции.
8. Найти производную функции.
9. Найти критические точки в промежутках возрастания и убывания функции.
10. На основании проведенного исследования построить график функции.

У нас есть отличные курсы по математике для учеников с 1 по 11 классы!

Видео:Алгебра 7 класс. 19 сентября. Числовые промежуткиСкачать

Построение графика функции

Чтобы понять, как строить графики функций, потренируемся на примерах.

Задача 1. Построим график функции

Упростим формулу функции:

при х ≠ -1.

График функции — прямая y = x — 1 с выколотой точкой M (-1; -2).

Задача 2. Построим график функции

Выделим в формуле функции целую часть:

График функции — гипербола, сдвинутая на 3 вправо по x и на 2 вверх по y и растянутая в 10 раз по сравнению с графиком функции

Выделение целой части — полезный прием, который применяется в решении неравенств, построении графиков и оценке целых величин.

Задача 3. По виду графика определить знаки коэффициентов общего вида функции y = ax2 + bx + c.

Вспомним, как параметры a, b и c определяют положение параболы.

Ветви вниз, следовательно, a 0.

Точка пересечения с осью Oy — c = 0.

Координата вершины , т.к. неизвестное число при делении на положительное дает отрицательный результат, то это число отрицательное, следовательно, b > 0.

Ветви вниз, следовательно, a 0.

Координата вершины , т.к. неизвестное число при делении на отрицательное дает в результате положительное, то это число отрицательное, следовательно, b

Как видим, k = 3 > 0 и угол наклона к оси Ox острый, b = -1 — смещение по оси Oy.

k = -1 > 0 и b = 2 можно сделать аналогичные выводы, как и в первом пункте.

k = 2 > 0 — угол наклона к оси Ox острый, B = 0 — график проходит через начало координат.

k = 0 — константная функция, прямая проходит через точку b = -1 и параллельно оси Ox.

Задача 5. Построить график функции

Это дробно-рациональная функция. Область определения функции D(y): x ≠ 4; x ≠ 0.

Нули функции: 3, 2, 6.

Промежутки знакопостоянства функции определим с помощью метода интервалов.

Вертикальные асимптоты: x = 0, x = 4.

Если x стремится к бесконечности, то у стремится к 1. Значит, y = 1 — горизонтальная асимптота.

Вот так выглядит график:

Задача 6. Построить графики функций:

б)

г)

д)

Когда сложная функция получена из простейшей через несколько преобразований, то преобразования графиков можно выполнить в порядке арифметических действий с аргументом.

а)

Преобразование в одно действие типа f(x) + a.

Сдвигаем график вверх на 1:

б)

Преобразование в одно действие типа f(x — a).

Сдвигаем график вправо на 1:

В этом примере два преобразования, выполним их в порядке действий: сначала действия в скобках f(x — a), затем сложение f(x) + a.

Сдвигаем график вправо на 1:

Сдвигаем график вверх на 2:

г)

Преобразование в одно действие типа

Растягиваем график в 2 раза от оси ординат вдоль оси абсцисс:

д)

Мы видим три преобразования вида f(ax), f (x + a), -f(x).

Чтобы выполнить преобразования, посмотрим на порядок действий: сначала умножаем, затем складываем, а уже потом меняем знак. Чтобы применить умножение ко всему аргументу модуля в целом, вынесем двойку за скобки в модуле.

Сжимаем график в два раза вдоль оси абсцисс:

Сдвигаем график влево на 1/2 вдоль оси абсцисс:

Отражаем график симметрично относительно оси абсцисс:

Видео:Как построить график линейной функции.Скачать

Как на графике в excel отметить точку

Видео:График с выколотой точкойСкачать

Маркеры на графике..

Объясните пожалуйста как на графике функции, точки, соответствующие нулевым и единичным значениям функции, пометить маркерами..

Знаю как поставить просто маркеры, с промежутками..
А как именно с такими условиями не представляю..

Помощь в написании контрольных, курсовых и дипломных работ здесь.

QCustomPlot. Позиция точки на нарисованном графике, выделение областей на графике
Доброго времени суток! Необходима помощь сообщества. Для ведущейся работы назрела необходимость.

Сделать интерполяцию между кривыми на полярном графике, чтобы найти на графике заданную точку
Здравствуйте, мне необходимо сделать интерполяцию между кривыми на полярном графике, чтобы найти на.

Маркеры
Для каждого места нужно установить свою иконку. Где это надо менять? Куда смотреть? .

Маркеры
В настройках учетной записи нужно сменить текст нескольких писем. Для этого мне нужно поставить.

Видео:10 класс, 43 урок, Уравнение касательной к графику функцииСкачать

Как в excel на графике подписать точки?

Как добавить в точечный график названия точек. Не координаты, а названия.

В скобках координаты (х,у). На графике нужны названия: Точка 1 и Точка А с возможностью поменять их автоматически по данным в ячейках.

Да уж в этих новомодных Экселях, начиная с версии 2007 все настолько запутано, что как говорится «без поллитры не поймешь». Действительно в более ранних версиях работа с элементами диаграмм была реально интуитивной: кликаешь по нужному элементу и изменяй его до умопомрачения.

Но давайте ближе к делу. За основу своего ответа я взял версию Экселя от 2010 года (других под рукой нет, может в более поздних версия все выглядит попроще — чуть позже я дам ссылку на описание, которое к версии 2010 года отношение имеет весьма приблизительное).

Так вот, порядок действий для достижения нужного вам результата будет такой:

Видео:Математика без Ху!ни. Нахождение асимптот, построение графика функции.Скачать

Точки пересечения графиков в Excel

Как найти точки пересечения графиков в Excel? Например, есть графики, отображающие несколько показателей. Далеко не всегда они будут пересекаться непосредственно на поле диаграммы. Но пользователю нужно показать те значения, в которых линии рассматриваемых явлений пересекаются. Рассмотрим на примере.

Строим графики с точками пересечений

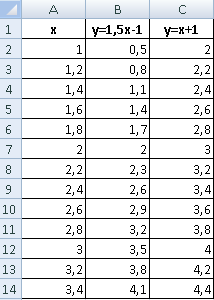
Имеются две функции, по которым нужно построить графики:

Выделяем диапазоны данных, на вкладке «Вставка» в группе «Диаграммы» подбираем нужный тип графика. Как:

1. Нужно найти точки пересечения графиков со значением Х, поэтому столбчатые, круговые, пузырьковые и т.п. диаграммы не выбираем. Это должны быть прямые линии.
2. Для поиска точек пересечения необходима ось Х. Не условная, на которой невозможно задать другое значение. Должна быть возможность выбирать промежуточные линии между периодами. Обычные графики не подходят. У них горизонтальная ось – общая для всех рядов. Периоды фиксированы. И манипулировать можно только с ними. Выберем точечную диаграмму с прямыми отрезками и маркерами.

Для данного типа диаграммы между основными периодами 0, 2, 4, 6 и т.д. можно использовать и промежуточные. Например, 2,5.

Находим точку пересечения графиков в Excel

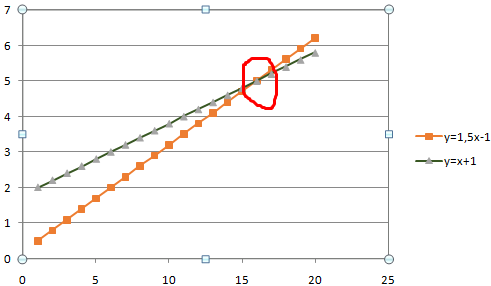
В табличном редакторе Excel нет встроенной функции для решения подобной задачи. Линии построенных графиков не пересекаются (см. рисунок), поэтому даже визуально точку пересечения найти нельзя. Ищем выход.

Первый способ. Найти общие значения в рядах данных для указанных функций.

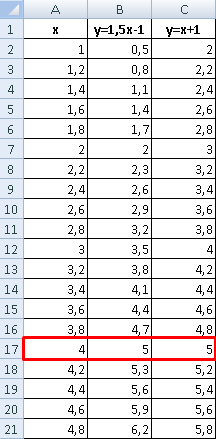
В таблице с данными таковых значений пока нет. Так как мы решали уравнения с помощью формул в полуавтоматическом режиме, с помощью маркера автозаполнения продолжим ряды данных.

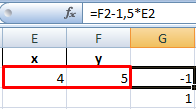
Значения Y одинаковые при Х = 4. Следовательно, точка пересечения двух графиков имеет координаты 4, 5.

Изменим график, добавив новые данные. Получим две пересекающиеся линии.

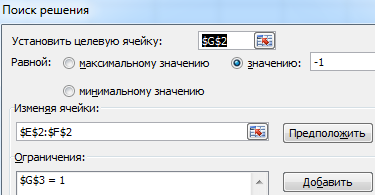
Второй способ. Применение для решения уравнений специального инструмента «Поиск решения». Кнопка вызова инструмента должна быть на вкладке «Данные». Если нет, нужно добавить из «Надстроек Excel».

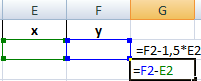
Преобразуем уравнения таким образом, чтобы неизвестные были в одной части: y – 1,5 х = -1; y – х = 1. Далее для неизвестных х и y назначим ячейки в Excel. Перепишем уравнения, используя ссылки на эти ячейки.

Вызываем меню «Поиск решения» — заполняем условия, необходимые для решения уравнений.

Нажимаем «Выполнить» — инструмент предлагает решение уравнений.

Найденные значения для х и y совпадают с предыдущим решением с помощью составления рядов данных.

Точки пересечения для трех показателей

Существует три показателя, которые измерялись во времени.

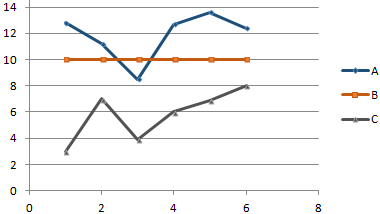
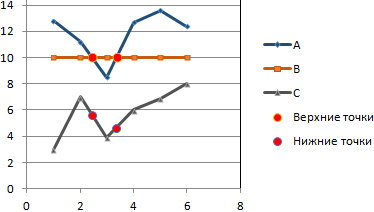
По условию задачи показатель В имеет постоянную величину на протяжении всех периодов. Это некий норматив. Показатель А зависит от показателя С. Он то выше, то ниже норматива. Строим графики (точечную диаграмму с прямыми отрезками и маркерами).

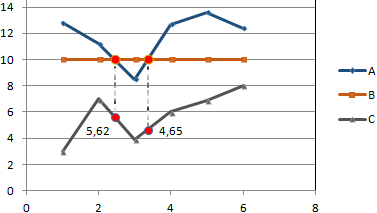
Точки пересечения имеются только у показателей А и В. Но их точные координаты нужно еще определить. Усложним задачу – найдем точки пересечения показателя C с показателями А и В. То есть в какие временные периоды и при каких значениях показателя А линия показателя С пересекает линию норматива.

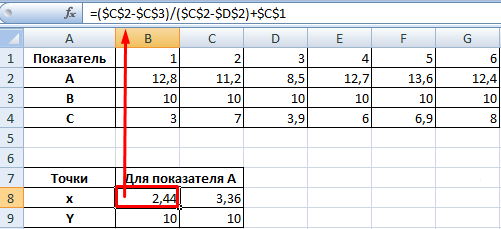
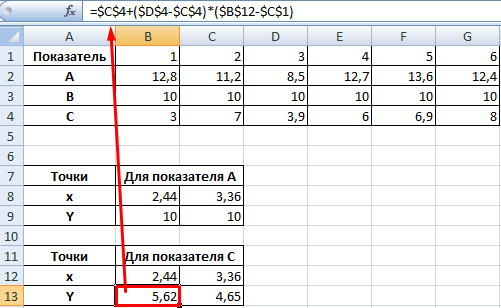
Точек у нас будет две. Их рассчитаем математическим путем. Сначала найдем точки пересечения показателя А с показателем В:

На рисунке видно, какие значения использовались для расчета. По такой же логике находим значение х для второй точки.

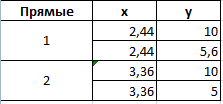
Теперь рассчитаем точки, найденных значений по оси Х с показателем С. Используем близкие формулы:

На основе новых данных построим точечные диаграммы на том же поле (где наши графики).

Получается такой рисунок:

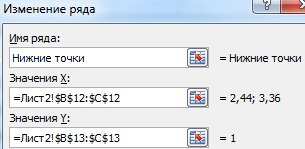
Для большей информативности и эстетики восприятия добавим пунктирные линии. Их координаты:

Добавим подписи данных – значения показателя C, при которых он пересечет линию норматива.

Можно форматировать графики по своему усмотрению – делать их более выразительными и наглядными.

Видео:Логарифмическая функция, ее свойства и график. 11 класс.Скачать

Алгебра. Урок 5. Графики функций

Смотрите бесплатные видео-уроки на канале Ёжику Понятно по теме “Графики функций”.

Видео-уроки на канале Ёжику Понятно. Подпишись!

Содержание страницы:

• Декартова система координат

• Функция

Видео:Линейная Функция — как БЫСТРО построить график и получить 5-куСкачать

Декартова система координат

Система координат – это две взаимно перпендикулярные координатные прямые, пересекающиеся в точке, которая является началом отсчета для каждой из них.

Координатные оси – прямые, образующие систему координат.

Ось абсцисс (ось x ) – горизонтальная ось.

Ось ординат (ось y ) – вертикальная ось.

Видео:Линейная функция и ее график. 7 класс.Скачать

Функция

Функция – это отображение элементов множества X на множество Y . При этом каждому элементу x множества X соответствует одно единственное значение y множества Y .

Видео:10 класс, 11 урок, Числовая окружностьСкачать

Прямая

Линейная функция – функция вида y = a x + b где a и b – любые числа.

Графиком линейной функции является прямая линия.

Рассмотрим, как будет выглядеть график в зависимости от коэффициентов a и b :

Если a > 0 , прямая будет проходить через I и III координатные четверти.

b – точка пересечения прямой с осью y .

Если a 0 , прямая будет проходить через II и IV координатные четверти.

b – точка пересечения прямой с осью y .

Если a = 0 , функция принимает вид y = b .

Отдельно выделим график уравнения x = a .

Важно : это уравнение не является функцией так как нарушается определение функции ( функция ставит в соответствие каждому элементу x множества X одно единственно значение y множества Y ). Данное уравнение ставит в соответствие одному элементу x бесконечное множества элементов y . Тем не менее, график данного уравнения построить можно. Просто не будем называть его гордым словом «Функция».

Видео:Точки пересечения графика линейной функции с координатными осями. Практическая часть. 7 класс.Скачать

Парабола

Графиком функции y = a x 2 + b x + c является парабола .

Для того, чтобы однозначно определить, как располагается график параболы на плоскости, нужно знать, на что влияют коэффициенты a , b , c :

1. Коэффициент a указывает на то, куда направлены ветки параболы.

• Если a > 0 , ветки параболы направлены вверх.
• Если a 0 , ветки параболы направлены вниз.

1. Коэффициент c указывает, в какой точке парабола пересекает ось y .
2. Коэффициент b помогает найти x в – координату вершины параболы.

1. Дискриминант позволяет определить, сколько точек пересечения у параболы с осью .

• Если D > 0 – две точки пересечения.
• Если D = 0 – одна точка пересечения.
• Если D 0 – нет точек пересечения.

Видео:Касательная к графику функции в точке. 10 класс.Скачать

Гипербола

Графиком функции y = k x является гипербола .

Характерная особенность гиперболы в том, что у неё есть асимптоты.

Асимптоты гиперболы – прямые, к которым она стремится, уходя в бесконечность.

Ось x – горизонтальная асимптота гиперболы

Ось y – вертикальная асимптота гиперболы.

На графике асимптоты отмечены зелёной пунктирной линией.

Если коэффициент k > 0 , то ветви гиперолы проходят через I и III четверти.

0″ height=»346″ width=»346″ sizes=»(max-width: 346px) 100vw, 346px» data-srcset=»/wp-content/uploads/2017/01/Гипербола-1.png 346w,/wp-content/uploads/2017/01/Гипербола-1-150×150.png 150w,/wp-content/uploads/2017/01/Гипербола-1-300×300.png 300w,/wp-content/uploads/2017/01/Гипербола-1-176×176.png 176w,/wp-content/uploads/2017/01/Гипербола-1-60×60.png 60w, https://epmat.ru/wp-content/uploads/2017/01/Гипербола-1.png»>

Если k 0, ветви гиперболы проходят через II и IV четверти.

Чем меньше абсолютная величина коэффиента k (коэффициент k без учета знака), тем ближе ветви гиперболы к осям x и y .

Видео:Как на диаграмме Excel отобразить проекции точек на оси координатСкачать

Квадратный корень

Функция y = x имеет следующий график:

Видео:Как запомнить графики функцийСкачать

Возрастающие/убывающие функции

Функция y = f ( x ) возрастает на интервале , если большему значению аргумента (большему значению x ) соответствует большее значение функции (большее значение y ) .

То есть чем больше (правее) икс, тем больше (выше) игрек. График поднимается вверх (смотрим слева направо)

Примеры возрастающих функций:

Функция y = f ( x ) убывает на интервале , если большему значению аргумента (большему значению x ) соответствует меньшее значение функции (большее значение y ) .

То есть чем больше (правее) икс, тем меньше (ниже) игрек. График опускается вниз (смотрим слева направо).

Примеры убывающих функций:

Для того, чтобы найти наибольшее значение функции , находим самую высокую точку на графике и смотрим, какая у нее координата по оси ординат (по оси y ) . Это значение и будет являться наибольшим значением функции.

Для того, чтобы найти наименьшее значение функции , находим самую нижнюю точку на графике и смотрим, какая у нее координата по оси ординат (по оси y ) . Это значение и будет являться наименьшим значением функции.

Видео:Уравнение окружности (1)Скачать

Задание №11 из ОГЭ 2020. Типовые задачи и принцип их решения.

💡 Видео

Линейная функция и её график. Алгебра, 7 классСкачать

Точки пересечения графиков линейных функций. 7 класс.ОбразовательныйСкачать