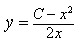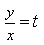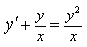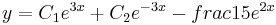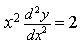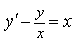Среди перечисленных дифференциальных уравнений укажите уравнение бернулли (6 видео)

Дифференциальное уравнение Бернулли

Статья раскрывает методы решения дифференциального уравнения Бернулли. В заключении будут рассмотрены решения примеров с подробным объяснением.

Содержание

Приведение к линейному уравнению 1 порядка
Представление произведением функций u ( x ) и v ( x )
Математика модуль 12 — ответы
Среди перечисленных дифференциальных уравнений укажите однородное уравнение
📽️ Видео

Видео:Дифференциальные уравнения, 5 урок, Уравнение БернуллиСкачать

Приведение к линейному уравнению 1 порядка

Дифференциальное уравнение Бернулли записывается как y ‘ + P ( x ) · y = Q ( x ) · y n . Если n = 1 , тогда его называют с разделяющими переменными. Тогда уравнение запишется как y ‘ + P ( x ) · y = Q ( x ) · y ⇔ y ‘ = Q ( x ) — P ( x ) · y .

Для того, чтобы решить такое уравнение, необходимо первоначально привести к линейному неоднородному дифференциальному уравнению 1 порядка с новой переменной вида z = y 1 — n . Проделав замену, получаем, что y = z 1 1 — n ⇒ y ‘ = 1 1 — n · z n 1 — n · z ‘ .

Отсюда вид уравнения Бернулли меняется:

y ‘ + P ( x ) · y = Q ( x ) · y n 1 1 — n · z 1 1 — n · z ‘ + P ( x ) · z 1 1 — n = Q ( x ) · z 1 1 — n z ‘ + ( 1 — n ) · P ( x ) · z = ( 1 — n ) · Q ( x )

Этот процесс вычисления и подстановки способствует приведению к линейному неоднородному дифференциальному уравнению первого порядка. В итоге проводим замену и получаем его решение.

Найти общее решение для уравнения вида y ‘ + x y = ( 1 + x ) · e — x · y 2 .

Решение

По условию имеем, что n = 2 , P ( x ) = x , Q ( x ) = ( 1 + x ) · e — x . Необходимо ввести новую переменную z = y 1 — n = y 1 — 2 = 1 y , отсюда получим, что y = 1 z ⇒ y ‘ = — z ‘ z 2 . Провести замену переменных и получить ЛНДУ первого порядка. Запишем, как

y ‘ + x y = ( 1 + x ) · e — x · y 2 — z ‘ z 2 + x z = ( 1 + x ) · e — x · 1 z 2 z ‘ — x z = — ( 1 + x ) · e — x

Следует проводить решение при помощи метода вариации произвольной постоянной.

Проводим нахождение общего решения дифференциального уравнения вида:

d z d x — x z = 0 ⇔ d z z = x d x , z ≠ 0 ∫ d z z = ∫ x d x ln z + C 1 = x 2 2 + C 2 e ln z + C 1 = e x 2 2 + C 2 z = C · e x 2 2 , C = e C 2 — C 1

Где z = 0 , тогда решение дифференциального уравнения считается z ‘ — x z = 0 , потому как тождество становится равным нулю при нулевой функции z . Данный случай записывается как z = C ( x ) · e x 2 2 , где С = 0 . Отсюда имеем, что общим решением дифференциального уравнения z ‘ — x z = 0 считается выражение z = C · e x 2 2 при С являющейся произвольной постоянной.

Необходимо варьировать переменную для того, чтобы можно было принять
z = C ( x ) · e x 2 2 как общее решение дифференциального уравнения вида z ‘ — x z = — ( 1 + x ) · e — x .

Отсюда следует, что производится подстановка вида

C ( x ) · e x 2 2 ‘ — x · C ( x ) · e x 2 2 = — ( 1 + x ) · e — x C ‘ ( x ) · e x 2 2 + C ( x ) · e x 2 2 ‘ — x · C ( x ) · e x 2 2 = — 1 + x · e — x C ‘ ( x ) · e x 2 2 + C ( x ) · x · e x 2 2 — x · C ( x ) · e x 2 2 = — ( 1 + x ) · e — x C ‘ ( x ) · e x 2 2 = — ( 1 + x ) · e — x 2 2 — x C ( x ) = ∫ — ( 1 + x ) · e — x 2 2 — x d x = ∫ e — x 2 2 — x d — x 2 2 — x = e — x 2 x — x + C 3

С 3 принимает значение произвольной постоянной. Следовательно:

z = C x · e x 2 2 = e — x 2 2 — x + C 3 · e x 2 2 = e — x + C 3 · e x 2 2

Дальше производится обратная замена. Следует, что z = 1 y считается за y = 1 z = 1 e — x + C 3 · e x 2 2 .

Ответ: это решение считается решением исходного дифференциального уравнения Бернулли.

Видео:7. Линейные дифференциальные уравнения первого порядка. Метод Бернулли.Скачать

Представление произведением функций u ( x ) и v ( x )

Имеется другой метод решения дифференциального уравнения Бернулли, который основывается на том, что функцию представляют при помощи произведения функций u ( x ) и v ( x ) .

Тогда получаем, что y ‘ = ( u · v ) ‘ = u ‘ · v + u · v ‘ . Производим подстановку в уравнение Бернулли y ‘ + P ( x ) · y = Q ( x ) · y n и упростим выражение:

u ‘ · v + u · v ‘ + P ( x ) · u · v = Q ( x ) · u · v n u ‘ · v + u · ( v ‘ + P ( x ) · v ) = Q ( x ) · u · v n

Когда в качестве функции берут ненулевое частное решение дифференциального уравнения v ‘ + P ( x ) · v = 0 , тогда придем к равенству такого вида

u ‘ · v + u · ( v ‘ + P ( x ) · v ) = Q ( x ) · ( u · v ) n ⇔ u ‘ · v = Q ( x ) · ( u · v ) n .

Отсюда следует определить функцию u .

Решить задачу Коши 1 + x 2 · y ‘ + y = y 2 · a r c t g x , y ( 0 ) = 1 .

Решение

Переходим к нахождению дифференциального уравнения вида 1 + x 2 · y ‘ = y · a r c t g x , которое удовлетворяет условию y ( 0 ) = 1 .

Обе части неравенства необходимо поделить на x 2 + 1 , после чего получим дифференциальное уравнение Бернулли y ‘ + y x 2 + 1 = y 2 · a r c t g x x 2 + 1 .

Перейдем к поиску общего решения.

Принимаем y = u · v , отсюда получаем, что y ‘ = u · v ‘ = u ‘ · v + u · v ‘ и уравнение запишем в виде

y ‘ + y x 2 + 1 = y 2 · a r c t g x x 2 + 1 u ‘ · v + u · v ‘ + u · v x 2 + 1 = u · v 2 · a r c t g x x 2 + 1 u ‘ · v + u · v ‘ + v x 2 + 1 = u 2 · v 2 · a r c t g x x 2 + 1

Проведем поиск частного решения с наличием разделяющих переменных v ‘ + v x 2 + 1 = 0 , отличных от нуля. Получим, что

d v v = — d x x 2 + 1 , v ≠ 0 ∫ d v v = — ∫ d x x 2 + 1 ln v + C 1 = — a r c t g x + C 2 v = C · e — a r c t g x , C = e C 2 — C 1

В качестве частного решения необходимо брать выражение вида v = e — a r c r g x . Преобразуем и получим, что

u ‘ · v + u · v ‘ + v x 2 + 1 = u 2 · v 2 · a r c r g x x 2 + 1 u ‘ · v + u · 0 = u 2 · v 2 · a r c t g x x 2 + 1 u ‘ = u 2 · v · a r c t g x x 2 + 1 u ‘ = u 2 · e — a r c t g x · a r c t g x x 2 + 1 ⇔ d u u 2 = e — a r c t g x · a r c t g x x 2 + 1 d x , u ≠ 0 ∫ d u u 2 = ∫ e — a r c t g x · a r c t g x x 2 + 1 d x ∫ d u u 2 = ∫ e — a r c t g x · a r c t g x d ( a r c t g x )

Имеем, что u = 0 рассматривается как решение дифференциального уравнения. Далее необходимо решить каждый из полученных интегралов по отдельности.

Интеграл с левой стороны, имеющего вид ∫ d u u 2 , необходимо найти по таблице первообразных. Получаем, что

∫ d u u 2 = — 1 u + C 3 .

Чтобы найти интеграл вида ∫ e — a r c t g x · a r c t g x d ( a r c t g x ) , принимаем значение a r c t g x = z и применяем метод интегрирования по частям. Тогда имеем, что

∫ e — a r c t g x · a r c t g x d ( a r c t g x ) = a r c t g x = z = = ∫ e — z · z d z = u 1 = z , d v 1 = e — z d z d u 1 = d z , v 1 = — e — z = = — z · e — z + ∫ e — z d z = — z · e — z — e — z + C 4 = = — e — z · ( z + 1 ) + C 4 = — e — a r c t g x · ( a r c t g x + 1 ) + C 4

— 1 u + C 3 = — e — a r c t g x · a r c t g x + 1 + C 4 1 u = e — a r c r g x · a r c t g x + 1 + C 3 — C 4 u = 1 e — a r c r g x · ( a r c t g x + 1 ) + C

Отсюда находим, что

y = u · v = e — a r c t g x e — a r c r g x · ( a r c t g x + 1 ) + C и y = 0 · v = 0 · e — a r c r g x = 0 являются решениями дифференциального уравнения Бернулли вида y ‘ + y x 2 + 1 = y 2 · a r c t g x x 2 + 1 .

На данном этапе следует переходить к поиску частного решения, которое удовлетворяет начальному условию. Получим, что

y = e — a r c t g x e — a r c t g x · a r c t g x + 1 + C , тогда запись примет вид y 0 = e — a r c t g 0 e — a r c t g 0 · a r c t g 0 + 1 + C = 1 1 + C .

Очевидно, что 1 1 + C = 1 ⇔ C = 0 . Тогда искомой задачей Коши будет являться полученное уравнение вида y = e — a r c t g x e — a r c t g x · a r c t g x + 1 + 0 = 1 a r c t g x + 1 .

Видео:10. Уравнения БернуллиСкачать