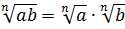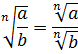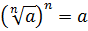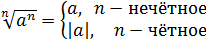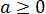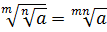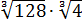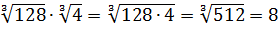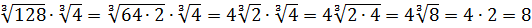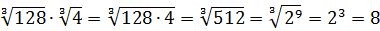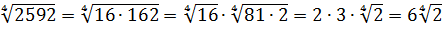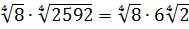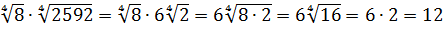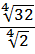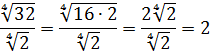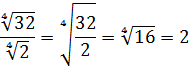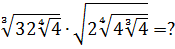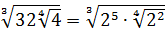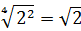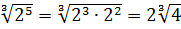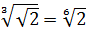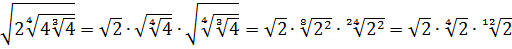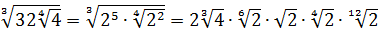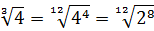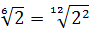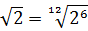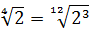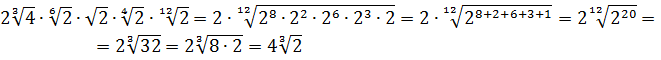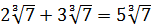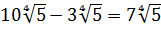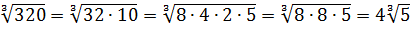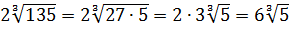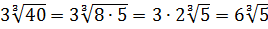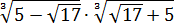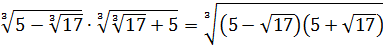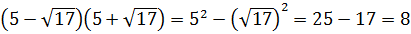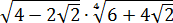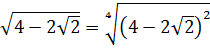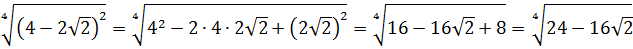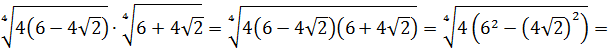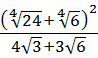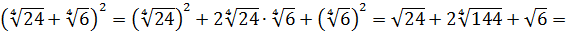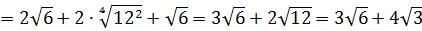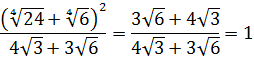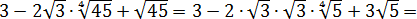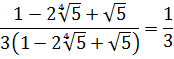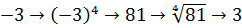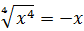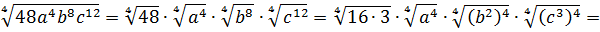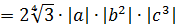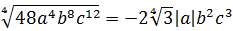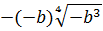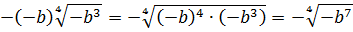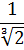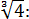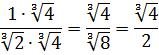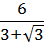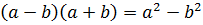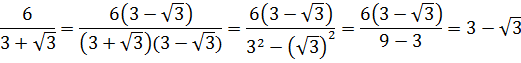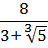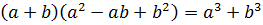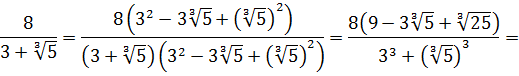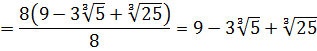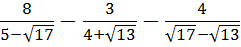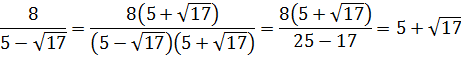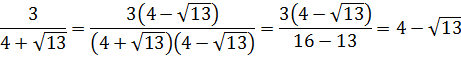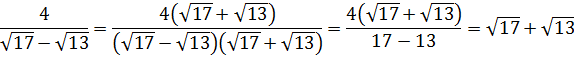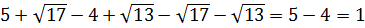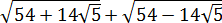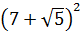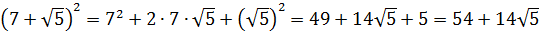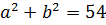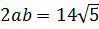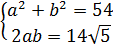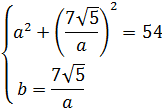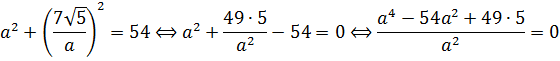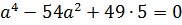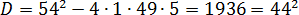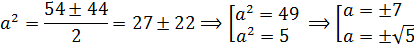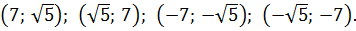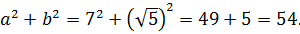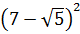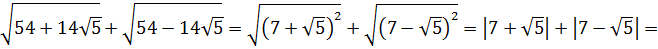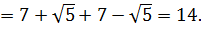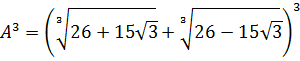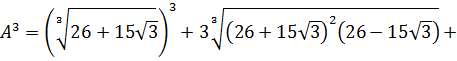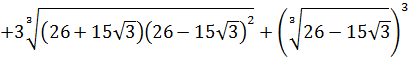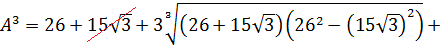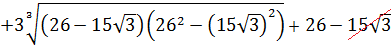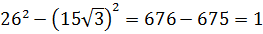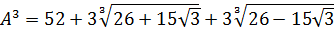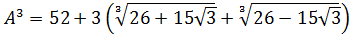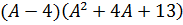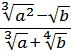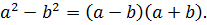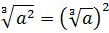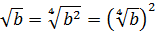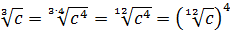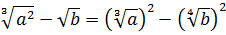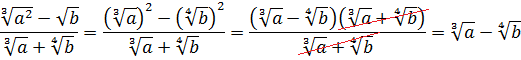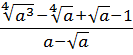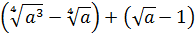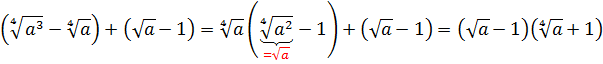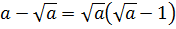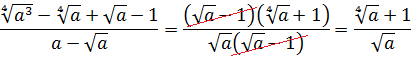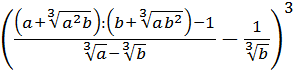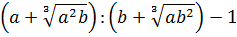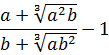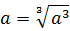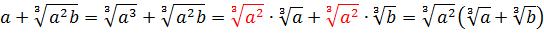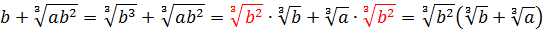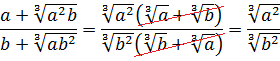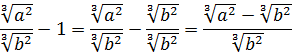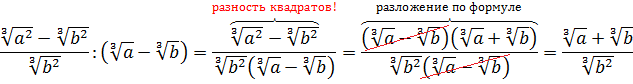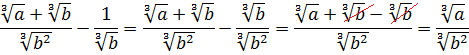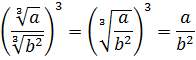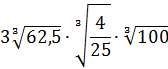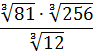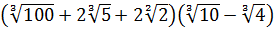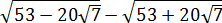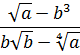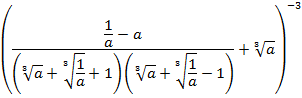Как освободиться от иррациональности в уравнение

Иррациональные выражения и их преобразования

В прошлый раз мы вспомнили (или узнали — кому как), что же такое корень n-й степени , научились извлекать такие корни, разобрали по винтикам основные свойства корней и решали несложные примеры с корнями.

Этот урок будет продолжением предыдущего и будет посвящён преобразованиям самых разных выражений, содержащих всевозможные корни. Такие выражения называются иррациональными. Здесь появятся и выражения с буквами, и дополнительные условия, и избавление от иррациональности в дробях, и некоторые продвинутые приёмы в работе с корнями. Те приёмы, которые будут рассматриваться в данном уроке, станут хорошей базой для решения задач ЕГЭ (и не только) практически любого уровня сложности. Итак, давайте приступим.

Прежде всего я продублирую здесь основные формулы и свойства корней. Чтобы не скакать из темы в тему. Вот они:

при

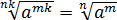
Формулы эти надо обязательно знать и уметь применять. Причём в обе стороны — как слева направо, так и справа налево. Именно на них и основывается решение большинства заданий с корнями любой степени сложности. Начнём пока с самого простого — с прямого применения формул или их комбинаций.

Простое применение формул

В этой части будут рассматриваться простые и безобидные примеры — без букв, дополнительных условий и прочих хитростей. Однако даже в них, как правило, имеются варианты. И чем навороченнее пример, тем больше таких вариантов. И у неопытного ученика возникает главная проблема — с чего начинать? Ответ здесь простой — не знаешь, что нужно — делай что можно. Лишь бы ваши действия шли в мире и согласии с правилами математики и не противоречили им.) Например, такое задание:

Вычислить:

Даже в таком простеньком примере возможны несколько путей к ответу.

Первый — просто перемножить корни по первому свойству и извлечь корень из результата:

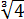
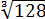
Второй вариант такой: не трогаем, работаем с . Выносим множитель из-под знака корня, а дальше — по первому свойству. Вот так:

Решать можно как больше нравится. В любом из вариантов ответ получается один — восьмёрка. Мне, например, проще перемножить 4 и 128 и получить 512, а из этого числа отлично извлекается кубический корень. Если кто-то не помнит, что 512 — это 8 в кубе, то не беда: можно записать 512 как 2 9 (первые 10 степеней двойки, я надеюсь, помните?) и по формуле корня из степени:

Вычислить: .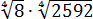

Если работать по первому свойству (всё загнать под один корень), то получится здоровенное число, из которого корень потом извлекать — тоже не сахар. Да и не факт, что он извлечётся ровно.) Поэтому здесь полезно в числе 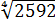вынести множители из-под корня. Причём вынести по максимуму:

И теперь всё наладилось:

Осталось восьмёрку и двойку записать под одним корнем (по первому свойству) и — готово дело. 🙂

Добавим теперь немного дробей.

Пример совсем примитивный, однако и в нём имеются варианты. Можно с помощью вынесения множителя преобразовать числитель и сократить со знаменателем:

А можно сразу воспользоваться формулой деления корней:

Как видим, и так, и сяк — всяко правильно.) Если не споткнуться на полпути и не ошибиться. Хотя где тут ошибаться-то…

Разберём теперь самый последний пример из домашнего задания прошлого урока:

Совершенно немыслимый набор корней, да ещё и вложенных. Как быть? Главное — не бояться! Здесь мы первым делом замечаем под корнями числа 2, 4 и 32 — степени двойки. Первое что нужно сделать — привести все числа к двойкам: всё-таки чем больше одинаковых чисел в примере и меньше разных, тем проще.) Начнём отдельно с первого множителя:

Число 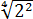можно упростить, сократив двойку под корнем с четвёркой в показателе корня:

Теперь, согласно корню из произведения:

.

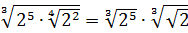
В числе 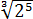выносим двойку за знак корня:

А с выражением 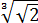расправляемся по формуле корня из корня:

Значит, первый множитель запишется вот так:

.

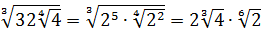
Вложенные корни исчезли, числа стали поменьше, что уже радует. Вот только корни разные, но пока так и оставим. Надо будет — преобразуем к одинаковым. Берёмся за второй множитель.)

Второй множитель преобразовываем аналогично, по формуле корня из произведения и корня из корня. Где надо — сокращаем показатели по пятой формуле:

Вставляем всё в исходный пример и получаем:

Получили произведение целой кучи совершенно разных корней. Неплохо было бы привести их все к одному показателю, а там — видно будет. Что ж, это вполне возможно. Наибольший из показателей корней равен 12, а все остальные — 2, 3, 4, 6 — делители числа 12. Поэтому будем приводить все корни по пятому свойству к одному показателю — к 12:

Считаем и получаем:

Красивого числа не получили, ну и ладно. Нас просили упростить выражение, а не посчитать. Упростили? Конечно! А вид ответа (целое число или нет) здесь уже не играет никакой роли.

Немного сложения / вычитания и формул сокращённого умножения

К сожалению, общих формул для сложения и вычитания корней в математике нету. Однако, в заданиях сплошь и рядом встречаются эти действия с корнями. Здесь необходимо понимать, что любые корни — это точно такие же математические значки, как и буквы в алгебре.) И к корням применимы те же самые приёмы и правила, что и к буквам — раскрытие скобок, приведение подобных, формулы сокращённого умножения и т.п.

Например, каждому ясно, что 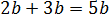. Точно так же одинаковые корни можно совершенно спокойно между собой складывать/вычитать:

Если корни разные, то ищем способ сделать их одинаковыми — внесением/вынесением множителя или же по пятому свойству. Если ну никак не упрощается, то, возможно, преобразования более хитрые.

Смотрим первый пример.

Найти значение выражения: .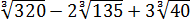

Все три корня хоть и кубические, но из разных чисел. Чисто не извлекаются и между собой складываются/вычитаются. Стало быть, применение общих формул здесь не катит. Как быть? А вынесем-ка множители в каждом корне. Хуже в любом случае не будет.) Тем более что других вариантов, собственно, и нету:

Стало быть, .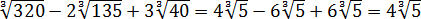

Вот и всё решение. Здесь мы от разных корней перешли к одинаковым с помощью вынесения множителя из-под корня. А затем просто привели подобные.) Решаем дальше.

Найти значение выражения:

С корнем из семнадцати точно ничего не поделаешь. Работаем по первому свойству — делаем из произведения двух корней один корень:

А теперь присмотримся повнимательнее. Что у нас под большим кубическим корнем? Разность ква.. Ну, конечно! Разность квадратов:

Теперь осталось только извлечь корень: .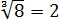

Дальше очень похожий пример, но посложнее.

Вычислить:

Здесь придётся проявить математическую смекалку.) Мыслим примерно следующим образом: «Так, в примере произведение корней. Под одним корнем разность, а под другим — сумма. Очень похоже на формулу разности квадратов. Но… Корни — разные! Первый квадратный, а второй — четвёртой степени… Хорошо бы сделать их одинаковыми. По пятому свойству можно легко из квадратного корня сделать корень четвёртой степени. Для этого достаточно подкоренное выражение возвести в квадрат.»

Если вы мыслили примерно так же, то вы — на полпути к успеху. Совершенно верно! Превратим первый множитель в корень четвёртой степени. Вот так:

Теперь, ничего не поделать, но придётся вспомнить формулу квадрата разности. Только в применении к корням. Ну и что? Чем корни хуже других чисел или выражений?! Возводим:

«Хм, ну возвели и что? Хрен редьки не слаще. Стоп! А если вынести четвёрку под корнем? Тогда выплывет то же самое выражение, что и под вторым корнем, только с минусом, а ведь именно этого мы и добиваемся!»

Верно! Выносим четвёрку:

.

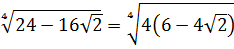
А теперь — дело техники:

.

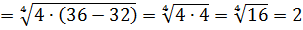
Вот так распутываются сложные примеры. ) Теперь пора потренироваться с дробями.

Ясно, что надо преобразовывать числитель. Как? По формуле квадрата суммы, разумеется. У нас есть ещё варианты разве? 🙂 Возводим в квадрат, выносим множители, сокращаем показатели (где надо):

Во как! Получили в точности знаменатель нашей дроби. ) Значит, вся дробь, очевидно, равна единице:

Ещё пример. Только теперь на другую формулу сокращённого умножения.)

Понятно, что квадрат разности надо в дело применять. Выписываем знаменатель отдельно и — поехали!

Выносим множители из-под корней:

Следовательно,

.

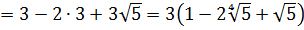
Теперь всё нехорошее великолепно сокращается и получается:

Что ж, поднимаемся на следующий уровень. 🙂

Буквы и дополнительные условия

Буквенные выражения с корнями — штука более хитрая, чем числовые выражения, и является неиссякаемым источником досадных и очень грубых ошибок. Перекроем этот источник.) Ошибки всплывают из-за того, что частенько таких заданиях фигурируют отрицательные числа и выражения. Они либо даны нам прямо в задании, либо спрятаны в буквах и дополнительных условиях. А нам в процессе работы с корнями постоянно надо помнить, что в корнях чётной степени как под самим корнем, так и в результате извлечения корня должно быть неотрицательное выражение. Ключевой формулой в задачах этого пункта будет четвёртая формула:

С корнями нечётной степени вопросов никаких — там всегда всё извлекается что с плюсом, что с минусом. И минус, если что, выносится вперёд. Будем сразу разбираться с корнями чётных степеней.) Например, такое коротенькое задание.

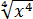
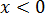
Упростить: , если .

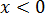
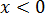
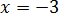
Казалось бы, всё просто. Получится просто икс. ) Но зачем же тогда дополнительное условие ? В таких случаях полезно прикинуть на числах. Чисто для себя.) Если , то икс — заведомо отрицательное число. Минус три, например. Или минус сорок. Пусть . Можно минус три возвести в четвёртую степень? Конечно! Получится 81. Можно из 81 извлечь корень четвёртой степени? А почему нет? Можно! Получится тройка. Теперь проанализируем всю нашу цепочку:

Что мы видим? На входе было отрицательное число, а на выходе — уже положительное. Было минус три, стало плюс три.) Возвращаемся к буквам. Вне всяких сомнений, по модулю это будет точно икс, но только сам икс у нас с минусом (по условию!), а результат извлечения (в силу арифметического корня!) должен быть с плюсом. Как получить плюс? Очень просто! Для этого достаточно перед заведомо отрицательным числом поставить минус.) И правильное решение выглядит так:

Кстати сказать, если бы мы воспользовались формулой 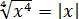, то, вспомнив определение модуля, сразу получили бы верный ответ. Поскольку

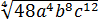
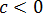
Вынести множитель за знак корня: , где .

Первый взгляд — на подкоренное выражение. Тут всё ОК. При любом раскладе оно будет неотрицательным. Начинаем извлекать. По формуле корня из произведения, извлекаем корень из каждого множителя:

Откуда взялись модули, объяснять, думаю, уже не надо.) А теперь анализируем каждый из модулей.

Множитель | a | так и оставляем без изменений: у нас нету никакого условия на букву a . Мы не знаем, положительное она или отрицательная. Следующий модуль | b 2 | можно смело опустить: в любом случае выражение b 2 неотрицательно. А вот насчёт | c 3 | — тут уже задачка.) Если 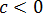, то и c 3 c 3 | = — c 3 . Итого верное решение будет такое:

А теперь — обратная задача. Не самая простая, сразу предупреждаю!

Внести множитель под знак корня: .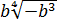

Если вы сразу запишете решение вот так

,

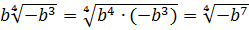
то вы попали в ловушку. Это неверное решение! В чём же дело?

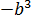
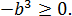
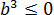
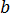
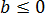
Давайте вглядимся в выражение под корнем . Под корнем четвёртой степени, как мы знаем, должно находиться неотрицательное выражение. Иначе корень смысла не имеет.) Поэтому А это, в свою очередь, значит, что и, следовательно, само также неположительно: .

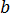
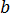
И ошибка здесь состоит в том, что мы вносим под корень неположительное число : четвёртая степень превращает его в неотрицательное и получается неверный результат — слева заведомый минус, а справа уже плюс. А вносить под корень чётной степени мы имеем право только неотрицательные числа или выражения. А минус, если есть, оставлять перед корнем.) Как же нам выделить неотрицательный множитель в числе , зная, что оно само стопудово отрицательное? Да точно так же! Поставить минус.) А чтобы ничего не поменялось, скомпенсировать его ещё одним минусом. Вот так:

И теперь уже неотрицательное число (-b) спокойно вносим под корень по всем правилам:

Этот пример наглядно показывает, что, в отличие от других разделов математики, в корнях правильный ответ далеко не всегда вытекает автоматически из формул. Необходимо подумать и лично принять верное решение.) Особенно следует быть внимательнее со знаками в иррациональных уравнениях и неравенствах.

Разбираемся со следующим важным приёмом в работе с корнями — избавлением от иррациональности.

Избавление от иррациональности в дробях

Если в выражении присутствуют корни, то, напомню, такое выражение называется выражением с иррациональностью. В некоторых случаях бывает полезно от этой самой иррациональности (т.е. корней) избавиться. Как можно ликвидировать корень? Корень у нас пропадает при… возведении в степень. С показателем либо равным показателю корня, либо кратным ему. Но, если мы возведём корень в степень (т.е. помножим корень сам на себя нужное число раз), то выражение от этого поменяется. Нехорошо.) Однако в математике бывают темы, где умножение вполне себе безболезненно. В дробях, к примеру. Согласно основному свойству дроби, если числитель и знаменатель умножить (разделить) на одно и то же число, то значение дроби не изменится.

Допустим, нам дана вот такая дробь:

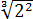
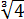
Можно ли избавиться от корня в знаменателе? Можно! Для этого корень надо возвести в куб. Чего нам не хватает в знаменателе для полного куба? Нам не хватает множителя , т.е. . Вот и домножаем числитель и знаменатель дроби на

Корень в знаменателе исчез. Но… он появился в числителе. Ничего не поделать, такова судьба.) Нам это уже не важно: нас просили знаменатель от корней освободить. Освободили? Безусловно.)

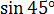
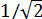
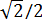
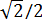
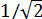
Кстати, те, кто уже в ладах с тригонометрией, возможно, обращали внимание на то, что в некоторых учебниках и таблицах, к примеру, обозначают по-разному: где-то , а где-то . Вопрос — что правильно? Ответ: всё правильно! ) Если догадаться, что – это просто результат освобождения от иррациональности в знаменателе дроби . 🙂

Зачем нам освобождаться от иррациональности в дробях? Какая разница — в числителе корень сидит или в знаменателе? Калькулятор всё равно всё посчитает.) Ну, для тех, кто не расстаётся с калькулятором, разницы действительно практически никакой… Но, даже считая на калькуляторе, можно обратить внимание на то, что делить на целое число всегда удобнее и быстрее, чем на иррациональное. А уж про деление в столбик вообще умолчу.)

Следующий пример только подтвердит мои слова.

Освободиться от иррациональности в знаменателе дроби:

Как здесь ликвидировать квадратный корень в знаменателе? Если числитель и знаменатель помножить на выражение 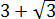, то в знаменателе получится квадрат суммы. Сумма квадратов первого и второго чисел дадут нам просто числа безо всяких корней, что очень радует. Однако… всплывёт удвоенное произведение первого числа на второе, где корень из трёх всё равно останется. Не канает. Как быть? Вспомнить другую замечательную формулу сокращённого умножения! Где никаких удвоенных произведений, а только квадраты:

Такое выражение, которое при домножении какой-то суммы (или разности) выводит на разность квадратов, ещё называют сопряжённым выражением. В нашем примере сопряжённым выражением будет служить разность 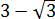. Вот и домножаем на эту разность числитель и знаменатель:

Что тут можно сказать? В результате наших манипуляций не то что корень из знаменателя исчез — вообще дробь исчезла! 🙂 Даже с калькулятором отнять корень из трёх от тройки проще, чем считать дробь с корнем в знаменателе. Ещё пример.

Освободиться от иррациональности в знаменателе дроби:

Как здесь выкручиваться? Формулы сокращённого умножения с квадратами сразу не катят — не получится полной ликвидации корней из-за того, что корень у нас в этот раз не квадратный, а кубический. Надо, чтобы корень как-то возвёлся в куб. Стало быть, применять надо какую-то из формул с кубами. Какую? Давайте подумаем. В знаменателе — сумма 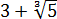. Как нам добиться возведения корня в куб? Домножить на неполный квадрат разности! Значит, применять будем формулу суммы кубов. Вот эту:

В качестве a у нас тройка, а в качестве b — корень кубический из пяти:

И снова дробь исчезла.) Такие ситуации, когда при освобождении от иррациональности в знаменателе дроби у нас вместе с корнями полностью исчезает сама дробь, встречаются очень часто. Как вам вот такой примерчик!

Попробуйте просто сложить эти три дроби! Без ошибок! 🙂 Один общий знаменатель чего стоит. А что, если попробовать освободиться от иррациональности в знаменателе каждой дроби? Что ж, пробуем:

Ух ты, как интересно! Все дроби пропали! Напрочь. И теперь пример решается в два счёта:

Просто и элегантно. И без долгих и утомительных вычислений. 🙂

Именно поэтому операцию освобождения от иррациональности в дробях надо уметь делать. В подобных навороченных примерах только она и спасает, да.) Разумеется, внимательность никто не отменял. Бывают задания, где просят избавиться от иррациональности в числителе. Эти задания ничем от рассмотренных не отличаются, только от корней очищается числитель.)

Более сложные примеры

Осталось рассмотреть некоторые специальные приёмы в работе с корнями и потренироваться распутывать не самые простые примеры. И тогда полученной информации уже будет достаточно для решения заданий с корнями любого уровня сложности. Итак — вперёд.) Для начала разберёмся, что делать со вложенными корнями, когда формула корня из корня не работает. Например, вот такой примерчик.

Вычислить:

Корень под корнем… К тому же под корнями сумма или разность. Стало быть, формула корня из корня (с перемножением показателей) здесь не действует. Значит, надо что-то делать с подкоренными выражениями: у нас просто нету других вариантов. В таких примерах чаще всего под большим корнем зашифрован полный квадрат какой-нибудь суммы. Или разности. А корень из квадрата уже отлично извлекается! И теперь наша задача — его расшифровать.) Такая расшифровка красиво делается через систему уравнений. Сейчас всё сами увидите.)

Итак, под первым корнем у нас вот такое выражение:

А вдруг, не угадали? Проверим! Возводим в квадрат по формуле квадрата суммы:

Всё верно.) Но… Откуда я взял это выражение 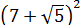? С неба?

Нет.) Мы его чуть ниже получим честно. Просто по данному выражению я показываю, как именно составители заданий шифруют такие квадраты. 🙂 Что такое 54? Это сумма квадратов первого и второго чисел. Причём, обратите внимание, уже без корней! А корень остаётся в удвоенном произведении, которое в нашем случае равно 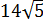. Поэтому распутывание подобных примеров начинается с поиска удвоенного произведения. Если распутывать обычным подбором. И, кстати, о знаках. Тут всё просто. Если перед удвоенным плюс, то квадрат суммы. Если минус, то разности.) У нас плюс — значит, квадрат суммы.) А теперь — обещанный аналитический способ расшифровки. Через систему.)

Итак, у нас под корнем явно тусуется выражение (a+b) 2 , и наша задача — найти a и b. В нашем случае сумма квадратов даёт 54. Вот и пишем:

Теперь удвоенное произведение. Оно у нас 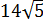. Так и записываем:

Получили вот такую системку:

Решаем обычным методом подстановки. Выражаем из второго уравнения, например, и подставляем в первое:

Решим первое уравнение:

Получили биквадратное уравнение относительно a . Считаем дискриминант:

Получили аж четыре возможных значения a . Не пугаемся. Сейчас мы всё лишнее отсеем.) Если мы сейчас для каждого из четырёх найденных значений посчитаем соответствующие значения , то получим четыре решения нашей системы. Вот они:

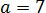
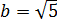
И тут вопрос — а какое из решений нам подходит? Давайте подумаем. Отрицательные решения можно сразу отбросить: при возведении в квадрат минусы «сгорят», и всё подкоренное выражение в целом не изменится.) Остаются первые два варианта. Выбрать их можно совершенно произвольно: от перестановки слагаемых сумма всё равно не меняется.) Пусть, например, , а .

Итого получили под корнем квадрат вот такой суммы:

Я не зря так детально описываю ход решения. Чтобы было понятно, как происходит расшифровка.) Но есть одна проблемка. Аналитический способ расшифровки хоть и надёжный, но весьма длинный и громоздкий: приходится решать биквадратное уравнение, получать четыре решения системы и потом ещё думать, какие из них выбрать… Хлопотно? Согласен, хлопотно. Этот способ безотказно работает в большинстве подобных примеров. Однако очень часто можно здорово сократить себе работу и найти оба числа творчески. Подбором.) Да-да! Сейчас, на примере второго слагаемого (второго корня), я покажу более лёгкий и быстрый способ выделения полного квадрата под корнем.

Итак, теперь у нас вот такой корень: .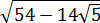

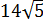
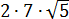
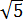
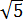
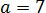
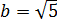
Размышляем так: «Под корнем — скорее всего, зашифрованный полный квадрат. Раз перед удвоенным минус — значит, квадрат разности. Сумма квадратов первого и второго чисел даёт нам число 54 . Но какие это квадраты? 1 и 53 ? 49 и 5 ? Слишком много вариантов… Нет, лучше начать распутывать с удвоенного произведения. Наши можно расписать как . Раз произведение удвоенное, то двойку сразу отметаем. Тогда кандидатами на роль a и b остаются 7 и . А вдруг, это 14 и /2 ? Не исключено. Но начинаем-то всегда с простого!» Итак, пусть , а . Проверим их на сумму квадратов:

Получилось! Значит, наше подкоренное выражение — это на самом деле квадрат разности:

Вот такой вот способ-лайт, чтобы не связываться с системой. Не всегда работает, но во многих таких примерах его вполне достаточно. Итак, под корнями — полные квадраты. Осталось только правильно извлечь корни, да досчитать пример:

А теперь разберём ещё более нестандартное задание на корни.)

Докажите, что число A – целое, если .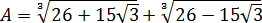

Впрямую ничего не извлекается, корни вложенные, да ещё и разных степеней… Кошмар! Однако, задание имеет смысл.) Стало быть, ключ к его решению имеется.) А ключ здесь такой. Рассмотрим наше равенство

как уравнение относительно A. Да-да! Хорошо бы избавиться от корней. Корни у нас кубические, поэтому возведём-ка обе части равенства в куб. По формуле куба суммы:

Кубы и корни кубические друг друга компенсируют, а под каждым большим корнем забираем одну скобку у квадрата и сворачиваем произведение разности и суммы в разность квадратов:

Отдельно сосчитаем разность квадратов под корнями:

Отлично! Значит, всё наше равенство ещё сильнее упростится:

А теперь делаем финт ушами — заменяем сумму корней в скобках на A (согласно условию примера!).

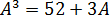
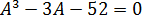
Получаем кубическое уравнение или .

Здесь как раз тот случай, когда один из корней легко угадывается — это 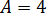. Значит, наш многочлен можно разложить как

Как разложить? Либо по схеме Горнера, либо делением «уголком» на скобку (A-4), либо даже группировкой (если представить -3A как -16A+13A). Объяснять подробно деление уголком или схему Горнера в теме про корни — уже совсем отклоняться от курса.) Кто в теме — и так поймёт.

А теперь легко заметить, что квадратный трёхчлен во вторых скобках имеет отрицательный дискриминант, а значит, наше уравнение имеет единственный действительный корень 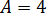. И поэтому наша страшная сумма корней в действительности равна просто 4. То есть, явно целому числу. Что и требовалось доказать.)

А теперь — поупрощаем некоторые дробные выражения с корнями. От простого — к сложному. Здесь всё точно так же, как и с многочленами. Только в применении к корням.) Я же говорил, что действия с корнями ничем не отличаются от таковых с буквами. И к корням с таким же успехом применима вся алгебра седьмого класса — формулы сокращённого умножения, разложение на множители, приведение подобных и т.п.

Например, такое задание.

Пример явно намекает на применение формулы разности квадратов:

Спрашивается, а где же здесь квадраты? Сплошные корни… Сейчас покажу. 🙂

Берём числитель нашей дробушки: .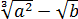

Что такое 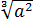? По свойству корня из степени, мы можем вынести квадрат наружу. Вот так:

Хорошо, а из 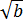как квадрат сделать? Не вопрос! По пятому свойству, домножаем на двойку показатели корня и подкоренного выражения:

По такой технологии, между прочим, можно совершенно любой корень превратить в совершенно любую степень. Какую хотим. 🙂 Как, например, 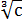представить в виде 4-й степени? Нет проблем:

Хотим из степеней корни делаем, хотим — наоборот, степени из корней. Что хотим, то и творим. Математика, однако! 🙂

Итак, весь наш числитель можно представить как разность квадратов:

А дальше никаких проблем — раскладываем числитель на множители и сокращаем:

Действуем аналогично. Раскладываем на множители и сокращаем. 🙂 В числителе применяем группировку. Например, вот такую:

А в знаменателе просто выносим общий множитель :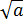

Подставляем всё в нашу дробь и сокращаем:

Как видим, разложение на множители очень популярно в теме с корнями. Очень! И особенно — формула разности квадратов. Именно поэтому формулы сокращённого умножения так важно знать и уметь применять. 🙂

Ну и на десерт распутаем что-нибудь навороченное. )

Чтобы не запутаться и не наляпать ошибок, будем действовать по порядку. При взгляде на любой пример всегда задаём сами себе вопрос: «Что в примере мне больше всего не нравится?» В данном примере большинство скажет: «Числитель первой дроби!» Верно! Вот и упростим его отдельно: остальная часть примера от этого никак не пострадает.) Итак,

Вместо знака деления удобно использовать черту дроби. Вот так:

Сначала упростим дробь. Как? Попробуем сократить.) Для этого, ясное дело, надо разложить на множители числитель и знаменатель, да… Берём отдельно числитель 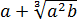. Можно его разложить на множители? Можно! Для этого из a надо сделать корень. Вот так:

Если теперь подставить вместо a выражение 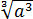, то всплывёт общий множитель. 🙂

Со знаменателем полная аналогия:

Теперь от упрощённой дроби отнимаем единичку. Как? Делаем из единички дробь и — вперёд!

Следующим пунктом идёт деление полученной дроби на выражение 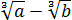. Это означает, что оно пойдёт у нас в знаменатель:

Уфф… Дальше… Отнимаем от полученного выражения дробь :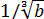

И, наконец, последнее усилие. Возводим результат в куб:

Ну как, всё понятно? Тогда — вперёд, набиваем руку и делаем примеры!

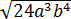
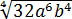
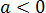
Вынести множители за знак корня: , , где .

Внести множители под знак корня: , .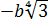

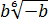
Освободиться от иррациональности в знаменателе дробей:

, .

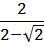
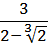
Вычислить:

Доказать, что A – целое число, если .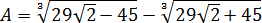

Ответы (пока) давать не буду — иначе неинтересно. 🙂 До встречи и успехов!

Видео:СУПЕР ЛАЙФХАК — Как решать Иррациональные УравненияСкачать

Как освободиться от иррациональности в знаменателе: способы, примеры, решения

При изучении преобразований иррационального выражения очень важным является вопрос о том, как освободиться от иррациональности в знаменателе дроби. Целью этой статьи является объяснение этого действия на конкретных примерах задач. В первом пункте мы рассмотрим основные правила данного преобразования, а во втором – характерные примеры с подробными пояснениями.

Видео:Преобразование выражений, содержащих квадратные корни. Избавление от иррациональности. 8 класс.Скачать

Понятие освобождения от иррациональности в знаменателе

Начнем с пояснения, в чем вообще заключается смысл такого преобразования. Для этого вспомним следующие положения.

Об иррациональности в знаменателе дроби можно говорить в том случае, если там присутствует радикал, он же знак корня. Числа, которые записаны при помощи такого знака, часто относятся к числу иррациональных. Примерами могут быть 1 2 , — 2 x + 3 , x + y x — 2 · x · y + 1 , 11 7 — 5 . К дробям с иррациональными знаменателями также относятся те, что имеют там знаки корней различной степени (квадратный, кубический и т.д.), например, 3 4 3 , 1 x + x · y 4 + y . Избавляться от иррациональности следует для упрощения выражения и облегчения дальнейших вычислений. Сформулируем основное определение:

Освободиться от иррациональности в знаменателе дроби – значит преобразовать ее, заменив на тождественно равную дробь, в знаменателе которой не содержится корней и степеней.

Такое действие может называться освобождением или избавлением от иррациональности, смысл при этом остается тем же. Так, переход от 1 2 к 2 2 , т.е. к дроби с равным значением без знака корня в знаменателе и будет нужным нам действием. Приведем еще один пример: у нас есть дробь x x — y . Проведем необходимые преобразования и получим тождественно равную ей дробь x · x + y x — y , освободившись от иррациональности в знаменателе.

После формулировки определения мы можем переходить непосредственно к изучению последовательности действий, которые нужно выполнить для такого преобразования.

Видео:Алгебра 8. Урок 8 - Квадратный корень. Освобождение от иррациональностиСкачать

Основные действия для избавления от иррациональности в знаменателе дроби

Для освобождения от корней нужно провести два последовательных преобразования дроби: умножить обе части дроби на число, отличное от нуля, а затем преобразовать выражение, получившееся в знаменателе. Рассмотрим основные случаи.

В наиболее простом случае можно обойтись преобразованием знаменателя. Например, мы можем взять дробь со знаменателем, равным корню из 9 . Вычислив 9 , мы запишем в знаменателе 3 и избавимся таким образом от иррациональности.

Однако гораздо чаще приходится предварительно умножать числитель и знаменатель на такое число, которое потом позволит привести знаменатель к нужному виду (без корней). Так, если мы выполним умножение 1 x + 1 на x + 1 , мы получим дробь x + 1 x + 1 · x + 1 и сможем заменить выражение в ее знаменателе на x + 1 . Так мы преобразовали 1 x + 1 в x + 1 x + 1 , избавившись от иррациональности.

Иногда преобразования, которые нужно выполнить, бывают довольно специфическими. Разберем несколько наглядных примеров.

Видео:Алгебра 8 класс. Избавляемся от иррациональности в знаменателеСкачать

Как преобразовать выражение в знаменателе дроби

Как мы уже говорили, проще всего выполнить преобразование знаменателя.

Условие: освободите дробь 1 2 · 18 + 50 от иррациональности в знаменателе.

Решение

Для начала раскроем скобки и получим выражение 1 2 · 18 + 2 · 50 . Используя основные свойства корней, перейдем к выражению 1 2 · 18 + 2 · 50 . Вычисляем значения обоих выражений под корнями и получаем 1 36 + 100 . Здесь уже можно извлечь корни. В итоге у нас получилась дробь 1 6 + 10 , равная 1 16 . На этом преобразования можно закончить.

Запишем ход всего решения без комментариев:

1 2 · 18 + 50 = 1 2 · 18 + 2 · 50 = = 1 2 · 18 + 2 · 50 = 1 36 + 100 = 1 6 + 10 = 1 16

Ответ: 1 2 · 18 + 50 = 1 16 .

Условие: дана дробь 7 — x ( x + 1 ) 2 . Избавьтесь от иррациональности в знаменателе.

Решение

Ранее в статье, посвященной преобразованиям иррациональных выражений с применением свойств корней, мы упоминали, что при любом A и четных n мы можем заменить выражение A n n на | A | на всей области допустимых значений переменных. Следовательно, в нашем случае мы можем записать так: 7 — x x + 1 2 = 7 — x x + 1 . Таким способом мы освободились от иррациональности в знаменателе.

Ответ: 7 — x x + 1 2 = 7 — x x + 1 .

Видео:Как решать уравнение с корнями Иррациональное уравнение Как решать уравнение с корнем х под корнемСкачать

Избавление от иррациональности методом умножения на корень

Если в знаменателе дроби находится выражение вида A и само выражение A не имеет знаков корней, то мы можем освободиться от иррациональности, просто умножив обе части исходной дроби на A . Возможность этого действия определяется тем, что A на области допустимых значений не будет обращаться в 0 . После умножения в знаменателе окажется выражение вида A · A , которое легко избавить от корней: A · A = A 2 = A . Посмотрим, как правильно применять этот метод на практике.

Условие: даны дроби x 3 и — 1 x 2 + y — 4 . Избавьтесь от иррациональности в их знаменателях.

Решение

Выполним умножение первой дроби на корень второй степени из 3 . Получим следующее:

x 3 = x · 3 3 · 3 = x · 3 3 2 = x · 3 3

Во втором случае нам надо выполнить умножение на x 2 + y — 4 и преобразовать получившееся выражение в знаменателе:

— 1 x 2 + y — 4 = — 1 · x 2 + y — 4 x 2 + y — 4 · x 2 + y — 4 = = — x 2 + y — 4 x 2 + y — 4 2 = — x 2 + y — 4 x 2 + y — 4

Ответ: x 3 = x · 3 3 и — 1 x 2 + y — 4 = — x 2 + y — 4 x 2 + y — 4 .

Если же в знаменателе исходной дроби имеются выражения вида A n m или A m n (при условии натуральных m и n ), нам нужно выбрать такой множитель, чтобы получившееся выражение можно было преобразовать в A n n · k или A n · k n (при натуральном k ). После этого избавиться от иррациональности будет несложно. Разберем такой пример.

Условие: даны дроби 7 6 3 5 и x x 2 + 1 4 15 . Избавьтесь от иррациональности в знаменателях.

Решение

Нам нужно взять натуральное число, которое можно разделить на пять, при этом оно должно быть больше трех. Чтобы показатель 6 стал равен 5 , нам надо выполнить умножение на 6 2 5 . Следовательно, обе части исходной дроби нам придется умножить на 6 2 5 :

7 6 3 5 = 7 · 6 2 5 6 3 5 · 6 2 5 = 7 · 6 2 5 6 3 5 · 6 2 = 7 · 6 2 5 6 5 5 = = 7 · 6 2 5 6 = 7 · 36 5 6

Во втором случае нам потребуется число, большее 15 , которое можно разделить на 4 без остатка. Берем 16 . Чтобы получить такой показатель степени в знаменателе, нам надо взять в качестве множителя x 2 + 1 4 . Уточним, что значение этого выражения не будет 0 ни в каком случае. Вычисляем:

x x 2 + 1 4 15 = x · x 2 + 1 4 x 2 + 1 4 15 · x 2 + 1 4 = = x · x 2 + 1 4 x 2 + 1 4 16 = x · x 2 + 1 4 x 2 + 1 4 4 4 = x · x 2 + 1 4 x 2 + 1 4

Ответ: 7 6 3 5 = 7 · 36 5 6 и x x 2 + 1 4 15 = x · x 2 + 1 4 x 2 + 1 4 .

Видео:Сможешь избавиться от иррациональности? Обычный корень и кубическийСкачать

Избавление от иррациональности методом умножения на сопряженное выражение

Следующий метод подойдет для тех случаев, когда в знаменателе исходной дроби стоят выражения a + b , a — b , a + b , a — b , a + b , a — b . В таких случаях нам надо взять в качестве множителя сопряженное выражение. Поясним смысл этого понятия.

Для первого выражения a + b сопряженным будет a — b , для второго a — b – a + b . Для a + b – a — b , для a — b – a + b , для a + b – a — b , а для a — b – a + b . Иначе говоря, сопряженное выражение – это такое выражение, в котором перед вторым слагаемым стоит противоположный знак.

Давайте рассмотрим, в чем именно заключается данный метод. Допустим, у нас есть произведение вида a — b · a + b . Оно может быть заменено разностью квадратов a — b · a + b = a 2 — b 2 , после чего мы переходим к выражению a − b , лишенному радикалов. Таким образом, мы освободились от иррациональности в знаменателе дроби с помощью умножения на сопряженное выражение. Возьмем пару наглядных примеров.

Условие: избавьтесь от иррациональности в выражениях 3 7 — 3 и x — 5 — 2 .

Решение

В первом случае берем сопряженное выражение, равное 7 + 3 . Теперь производим умножение обеих частей исходной дроби на него:

3 7 — 3 = 3 · 7 + 3 7 — 3 · 7 + 3 = 3 · 7 + 3 7 2 — 3 2 = = 3 · 7 + 3 7 — 9 = 3 · 7 + 3 — 2 = — 3 · 7 + 3 2

Во втором случае нам понадобится выражение — 5 + 2 , которое является сопряженным выражению — 5 — 2 . Умножим на него числитель и знаменатель и получим:

x — 5 — 2 = x · — 5 + 2 — 5 — 2 · — 5 + 2 = = x · — 5 + 2 — 5 2 — 2 2 = x · — 5 + 2 5 — 2 = x · 2 — 5 3

Возможно также перед умножением выполнить преобразование: если мы вынесем из знаменателя сначала минус, считать будет удобнее:

x — 5 — 2 = — x 5 + 2 = — x · 5 — 2 5 + 2 · 5 — 2 = = — x · 5 — 2 5 2 — 2 2 = — x · 5 — 2 5 — 2 = — x · 5 — 2 3 = = x · 2 — 5 3

Ответ: 3 7 — 3 = — 3 · 7 + 3 2 и x — 5 — 2 = x · 2 — 5 3 .

Важно обратить внимание на то, чтобы выражение, полученное в итоге умножения, не обращалось в 0 ни при каких переменных из области допустимых значений для данного выражения.

Условие: дана дробь x x + 4 . Преобразуйте ее так, чтобы в знаменателе не было иррациональных выражений.

Решение

Начнем с нахождения области допустимых значений переменной x . Она определена условиями x ≥ 0 и x + 4 ≠ 0 . Из них можно сделать вывод, что нужная область представляет собой множество x ≥ 0 .

Сопряженное знаменателю выражение представляет собой x — 4 . Когда мы можем выполнить умножение на него? Только в том случае, если x — 4 ≠ 0 . На области допустимых значений это будет равносильно условию x≠16. В итоге мы получим следующее:

x x + 4 = x · x — 4 x + 4 · x — 4 = = x · x — 4 x 2 — 4 2 = x · x — 4 x — 16

Если x будет равен 16 , то мы получим:

x x + 4 = 16 16 + 4 = 16 4 + 4 = 2

Следовательно, x x + 4 = x · x — 4 x — 16 при всех значениях x , принадлежащих области допустимых значений, за исключением 16 . При x = 16 получим x x + 4 = 2 .

Ответ: x x + 4 = x · x — 4 x — 16 , x ∈ [ 0 , 16 ) ∪ ( 16 , + ∞ ) 2 , x = 16 .

Видео:как избавиться от иррациональности в знаменателеСкачать

Преобразование дробей с иррациональностью в знаменателе с использованием формул суммы и разности кубов

В предыдущем пункте мы выполняли умножение на сопряженные выражения с тем, чтобы потом использовать формулу разности квадратов. Иногда для избавления от иррациональности в знаменателе полезно воспользоваться и другими формулами сокращенного умножения, например, разностью кубов a 3 − b 3 = ( a − b ) · ( a 2 + a · b + b 2 ) . Этой формулой удобно пользоваться, если в знаменателе исходной дроби стоят выражения с корнями третьей степени вида A 3 — B 3 , A 3 2 + A 3 · B 3 + B 3 2 . и т.д. Чтобы применить ее, нам нужно умножить знаменатель дроби на неполный квадрат суммы A 3 2 + A 3 · B 3 + B 3 2 или разность A 3 — B 3 . Точно также можно применить и формулу суммы a 3 + b 3 = ( а ) · ( a 2 − a · b + b 2 ) .

Условие: преобразуйте дроби 1 7 3 — 2 3 и 3 4 — 2 · x 3 + x 2 3 так, чтобы избавиться от иррациональности в знаменателе.

Решение

Для первой дроби нам нужно воспользоваться методом умножения обеих частей на неполный квадрат суммы 7 3 и 2 3 , поскольку потом мы сможем выполнить преобразование с помощью формулы разности кубов:

1 7 3 — 2 3 = 1 · 7 3 2 + 7 3 · 2 3 + 2 3 2 7 3 — 2 3 · 7 3 2 + 7 3 · 2 3 + 2 3 2 = = 7 3 2 + 7 3 · 2 3 + 2 3 2 7 3 3 — 2 3 3 = 7 2 3 + 7 · 2 3 + 2 2 3 7 — 2 = = 49 3 + 14 3 + 4 3 5

Во второй дроби представим знаменатель как 2 2 — 2 · x 3 + x 3 2 . В этом выражении виден неполный квадрат разности 2 и x 3 , значит, мы можем умножить обе части дроби на сумму 2 + x 3 и воспользоваться формулой суммы кубов. Для этого должно быть соблюдено условие 2 + x 3 ≠ 0 , равносильное x 3 ≠ — 2 и x ≠ − 8 :

3 4 — 2 · x 3 + x 2 3 = 3 2 2 — 2 · x 3 + x 3 2 = = 3 · 2 + x 3 2 2 — 2 · x 3 + x 3 2 · 2 + x 3 = 6 + 3 · x 3 2 3 + x 3 3 = = 6 + 3 · x 3 8 + x

Подставим в дробь — 8 и найдем значение:

3 4 — 2 · 8 3 + 8 2 3 = 3 4 — 2 · 2 + 4 = 3 4

Подведем итоги. При всех x , входящих в область значений исходной дроби (множество R ), за исключением — 8 , мы получим 3 4 — 2 · x 3 + x 2 3 = 6 + 3 · x 3 8 + x . Если x = 8 , то 3 4 — 2 · x 3 + x 2 3 = 3 4 .

Ответ: 3 4 — 2 · x 3 + x 2 3 = 6 + 3 · x 3 8 + x , x ≠ 8 3 4 , x = — 8 .

Видео:Уравнения с корнем. Иррациональные уравнения #shortsСкачать

Последовательное применение различных способов преобразования

Часто на практике встречаются более сложные примеры, когда мы не можем освободиться от иррациональности в знаменателе с помощью всего одного метода. Для них нужно последовательно выполнять несколько преобразований или подбирать нестандартные решения. Возьмем одну такую задачу.

Условие: преобразуйте 5 7 4 — 2 4 , чтобы избавиться от знаков корней в знаменателе.

Решение

Выполним умножение обеих частей исходной дроби на сопряженное выражение 7 4 + 2 4 с ненулевым значением. Получим следующее:

5 7 4 — 2 4 = 5 · 7 4 + 2 4 7 4 — 2 4 · 7 4 + 2 4 = = 5 · 7 4 + 2 4 7 4 2 — 2 4 2 = 5 · 7 4 + 2 4 7 — 2

А теперь применим тот же способ еще раз:

5 · 7 4 + 2 4 7 — 2 = 5 · 7 4 + 2 4 · 7 + 2 7 — 2 · 7 + 2 = = 5 · 7 4 + 2 4 · 7 + 2 7 2 — 2 2 = 5 · 7 4 + 7 4 · 7 + 2 7 — 2 = = 5 · 7 4 + 2 4 · 7 + 2 5 = 7 4 + 2 4 · 7 + 2

Ответ: 5 7 4 — 2 4 = 7 4 + 2 4 · 7 + 2 .

Видео:Как избавиться от иррациональности в знаменателеСкачать

Алгебра

План урока:

Видео:Избавление от иррациональности в знаменателе дробиСкачать

Иррациональные уравнения

Ранее мы рассматривали целые и дробно-рациональные уравнения. В них выражение с переменной НЕ могло находиться под знаком радикала, а также возводиться в дробную степень. Если же переменная оказывается под радикалом, то получается иррациональное уравнение.

Приведем примеры иррациональных ур-ний:

Заметим, что не всякое уравнение, содержащее радикалы, является иррациональным. В качестве примера можно привести

Это не иррациональное, а всего лишь квадратное ур-ние. Дело в том, что под знаком радикала стоит только число 5, а переменных там нет.

Видео:8 причин прокрастинации - советы для студентов и школьников от лектора с физтехаСкачать

Простейшие иррациональные уравнения

Начнем рассматривать способы решения иррациональных уравнений. В простейшем случае в нем справа записано число, а вся левая часть находится под знаком радикала. Выглядит подобное ур-ние так:

где а – некоторое число (константа), f(x) – рациональное выражение.

Для его решения необходимо обе части возвести в степень n, тогда корень исчезнет:

Получаем рациональное ур-ние, решать которые мы уже умеем. Однако есть важное ограничение. Мы помним, что корень четной степени всегда равен положительному числу, и его нельзя извлекать из отрицательного числа. Поэтому, если в ур-нии

n – четное число, то необходимо, чтобы а было положительным. Если же оно отрицательное, то ур-ние не имеет корней. Но на нечетные n такое ограничение не распространяется.

Пример. Решите ур-ние

Решение. Справа стоит отрицательное число (– 6), но квадратный корень (если быть точными, то арифметический квадратный корень) не может быть отрицательным. Поэтому ур-ние корней не имеет.

Ответ: корней нет.

Пример. Решите ур-ние

Решение. Теперь справа стоит положительное число, значит, мы имеем право возвести обе части в квадрат. При этом корень слева исчезнет:

Пример. Решите ур-ние

Решение. Справа стоит отрицательное число, но это не является проблемой, ведь кубический корень может быть отрицательным. Возведем обе части в куб:

Конечно, под знаком корня может стоять и более сложное выражение, чем (х – 5).

Пример. Найдите решение ур-ния

Решение. Возведем обе части в пятую степень:

х 2 – 14х – 32 = 0

Получили квадратное ур-ние, которое можно решить с помощью дискриминанта:

D = b 2 – 4ac = (– 14) 2 – 4•1•(– 32) = 196 + 128 = 324

Итак, нашли два корня: (– 2) и 16.

Несколько более сложным является случай, когда справа стоит не постоянное число, а какое-то выражение с переменной g(x). Алгоритм решения тот же самый – необходимо возвести в степень ур-ние, чтобы избавиться от корня. Но, если степень корня четная, то необходимо проверить, что полученные корни ур-ния не обращают правую часть, то есть g(x), в отрицательное число. В противном случае их надо отбросить как посторонние корни.

Пример. Решите ур-ние

Решение. Возводим обе части во вторую степень:

х – 2 = х 2 – 8х + 16

D = b 2 – 4ac = (– 9) 2 – 4•1•18 = 81 – 72 = 9

Получили два корня, 3 и 6. Теперь проверим, во что они обращают правую часть исходного ур-ния (х – 4):

при х = 3 х – 4 = 3 – 4 = – 1

при х = 6 6 – 4 = 6 – 4 = 2

Корень х = 3 придется отбросить, так как он обратил правую часть в отрицательное число. В результате остается только х = 6.

Пример. Решите ур-ние

Решение. Здесь используется кубический корень, а потому возведем обе части в куб:

3х 2 + 6х – 25 = (1 – х) 3

3х 2 + 6х – 25 = 1 – 3х + 3х 2 – х 3

Получили кубическое ур-ние. Решить его можно методом подбора корня. Из всех делителей свободного коэффициента (– 26) только двойка обращает ур-ние в верное равенство:

Других корней нет. Это следует из того факта, что функция у = х 3 + 9х – 26 является монотонной.

Заметим, что если подставить х = 2 в левую часть исходного ур-ния 1 – х, то получится отрицательное число:

при х = 2 1 – х = 1 – 2 = – 1

Но означает ли это, что число 2 НЕ является корнем? Нет, ведь кубический корень вполне может быть и отрицательным (в отличие от квадратного). На всякий случай убедимся, что двойка – это действительно корень исходного уравнения:

Видео:Избавиться от иррациональности в знаменателе 1/(√2+√3+√5)Скачать

Уравнения с двумя квадратными корнями

Ситуация осложняется, если в ур-нии есть сразу два квадратных корня. В этом случае их приходится убирать последовательно. Сначала мы переносим слагаемые через знак «=» таким образом, чтобы слева остался один из радикалов и ничего, кроме него. Возводя в квадрат такое ур-ние, мы избавимся от одного радикала, после чего мы получим более простое ур-ние. После получения всех корней надо проверить, какие из них являются посторонними. Для этого их надо просто подставить в исходное ур-ние.

Пример. Решите ур-ние

Решение. Перенесем вправо один из корней:

Возведем обе части в квадрат. Обратите внимание, что левый корень при этом исчезнет, а правый – сохранится:

Теперь снова перемещаем слагаемые так, чтобы в одной из частей не осталось ничего, кроме корня:

Снова возведем ур-ние в квадрат, чтобы избавиться и от второго корня:

(2х – 4) 2 = 13 – 3х

4х 2 – 16х + 16 = 13 – 3х

4х 2 – 13х + 3 = 0

D = b 2 – 4ac = (– 13) 2 – 4•4•3 = 169 –48 = 121

Имеем два корня: 3 и 0,25. Но вдруг среди них есть посторонние? Для проверки подставим их в исходное ур-ние. При х = 0,25 имеем:

Получилось ошибочное равенство, а это значит, что 0,25 не является корнем ур-ния. Далее проверим х = 3

На этот раз получилось справедливое равенство. Значит, тройка является корнем ур-ния.

Видео:Урок 29 (осн). Задачи по теме "Плотность" - 1Скачать

Введение новых переменных

Предложенный метод последовательного исключения радикалов плохо работает в том случае, если корни не квадратные, а имеют другую степень. Рассмотрим ур-ние

Последовательно исключить корни, как в предыдущем примере, здесь не получится (попробуйте это сделать самостоятельно). Однако помочь может замена переменной.

Для начала перепишем ур-ние в более удобной форме, когда вместо корней используются степени:

х 1/2 – 10х 1/4 + 9 = 0

Теперь введем переменную t = x 1/4 . Тогда х 1/2 = (х 1/4 ) 2 = t 2 . Исходное ур-ние примет вид

Это квадратное ур-ние. Найдем его корни:

D = b 2 – 4ac = (– 10) 2 – 4•1•9 = 100 – 36 = 64

Получили два значения t. Произведем обратную замену:

х 1/4 = 1 или х 1/4 = 9

Возведем оба ур-ния в четвертую степень:

(х 1/4 ) 4 = 1 4 или (х 1/4 ) 4 = 3 4

х = 1 или х = 6561

Полученные числа необходимо подставить в исходное ур-ние и убедиться, что они не являются посторонними корнями:

В обоих случаях мы получили верное равенство 0 = 0, а потому оба числа, 1 и 6561, являются корнями ур-ния.

Пример. Решите ур-ние

х 1/3 + 5х 1/6 – 24 = 0

Решение. Произведем замену t = x 1/6 , тогда х 1/3 = (х 1/6 ) 2 = t 2 . Исходное ур-ние примет вид:

Его корни вычислим через дискриминант:

D = b 2 – 4ac = 5 2 – 4•1•(– 24) = 25 + 96 = 121

Далее проводим обратную заменуx 1/6 = t:

х 1/6 = – 8 или х 1/6 = 3

Первое ур-ние решений не имеет, а единственным решением второго ур-ния является х = 3 6 = 729. Если подставить это число в исходное ур-ние, то можно убедиться, что это не посторонний корень.

Видео:8 класс, 38 урок, Иррациональные уравненияСкачать

Замена иррационального уравнения системой

Иногда для избавления от радикалов можно вместо них ввести дополнительные переменные и вместо одного иррационального ур-ния получить сразу несколько целых, которые образуют систему. Это один из самых эффективных методов решения иррациональных уравнений.

Пример. Решите ур-ние

Решение. Заменим первый корень буквой u, а второй – буквой v:

Исходное ур-ние примет вид

Если возвести (1) и (2) в куб и квадрат соответственно (чтобы избавиться от корней), то получим:

Ур-ния (3), (4) и (5) образуют систему с тремя неизвестными, в которой уже нет радикалов:

Попытаемся ее решить. Сначала сложим (4) и (5), ведь это позволит избавиться от переменной х:

(х + 6) + (11 – х) = u 3 + v 2

из (3) можно получить, что v = 5 – u. Подставим это в (6) вместо v:

17 = u 3 + (5 – u) 2

17 = u 3 + u 2 – 10u + 25

u 3 + u 2 – 10u + 8 = 0

Получили кубическое ур-ние. Мы уже умеем решать их, подбирая корни. Не вдаваясь в подробности решения, укажем, что корнями этого ур-ния являются числа

подставим полученные значения в (4):

x + 6 = 1 3 или х + 6 = 2 3 или х + 6 = (– 4) 3

x + 6 = 1 или х + 6 = 8 или х + 6 = – 64

х = – 5 или х = 2 или х = – 70

Итак, нашли три возможных значения х. Но, конечно же, среди них могут оказаться посторонние корни. Поэтому нужна проверка – подставим полученные результаты в исходное ур-ние. При х = – 5 получим

Корень подошел. Проверяем следующее число, х = 2:

Корень снова оказался верным. Осталась последняя проверка, для х = – 70:

Итак, все три числа прошли проверку.

Видео:Освобождение от иррациональности (радикалов) в знаменателе дробиСкачать

Уравнения с «вложенными» радикалами

Порою в ур-нии под знаком радикала стоит ещё один радикал. В качестве примера приведем такую задачу:

При их решении следует сначала избавиться от «внешнего радикала», после чего можно будет заняться и внутренним. То есть в данном случае надо сначала возвести обе части равенства в квадрат:

Внешний радикал исчез. Теперь будем переносить слагаемые, чтобы в одной из частей остался только радикал:

Хочется поделить полученное ур-ние (1) на х, однако важно помнить, что деление на ноль запрещено. То есть, если мы делим на х, то мы должны наложить дополнительное ограничение х ≠ 0. Случай же, когда х всё же равен нулю, мы рассматриваем отдельно. Для этого подставим х = 0 сразу в исходное ур-ние:

Получили верное рав-во, значит, 0 является корнем. Теперь возвращаемся к (1) и делим его на х:

Возводим в квадрат и получаем:

х 2 + 40 = (х + 4) 2

х 2 + 40 = х 2 + 8х + 16

И снова нелишней будет проверка полученного корня:

Видео:Как разобраться в корнях ? Квадратный корень 8 класс | Математика TutorOnlineСкачать

Иррациональные неравенства

По аналогии с иррациональными ур-ниями иррациональными неравенствами называют такие нер-ва, в которых выражение с переменной находится под знаком радикала или возводится в дробную степень. Приведем примеры иррациональных нер-в:

Нет смысла решать иррациональные нер-ва, если есть проблемы с более простыми, то есть рациональными нер-вами, а также с их системами. Поэтому на всякий случай ещё раз просмотрите этот и ещё вот этот уроки.

Начнем с решения иррациональных неравенств простейшего вида, у которых в одной из частей стоит выражение под корнем, а в другой – постоянное число. Достаточно очевидно, что нер-во вида

Может быть справедливым только тогда, когда

То есть, грубо говоря, нер-ва можно возводить в степень. Однако при этом могут возникнуть посторонние решения. Дело в том, что нужно учитывать и тот факт, что подкоренное выражение должно быть неотрицательным в том случае, если степень корня является четной. Таким образом, нер-во

при четном n можно заменить системой нер-в

Пример. При каких значениях x справедливо нер-во

Решение. С одной стороны, при возведении нер-ва в квадрат мы получим такое нер-во:

х ⩽ – 5 (знак нер-ва изменился из-за того, что мы поделили его на отрицательное число)

Получили промежуток х∈(– ∞; – 5). Казалось бы, надо записать ещё одно нер-во

чтобы подкоренное выражение было неотрицательным. Однако сравните (1) и (2). Ясно, что если (1) выполняется, то справедливым будет и (2), ведь если какое-то выражение больше или равно двум, то оно автоматически будет и больше нуля! Поэтому (2) можно и не решать.

Теперь посмотрим на простейшие нер-ва с корнем нечетной степени.

Пример. Найдите решение нер-ва

Решение. Всё очень просто – надо всего лишь возвести обе части в куб:

x 2 – 7x– 8 2 – 7x– 8 = 0

D = b 2 – 4ac = (– 7) 2 – 4•1•(– 8) = 49 + 32 = 81

Далее полученные точки отмечаются на координатной прямой. Они разобьют ее на несколько промежутков, на каждом из которых функция у =x 2 – 7x– 8 сохраняет свой знак. Определить же этот самый знак можно по направлению ветвей параболы, которую рисует схематично:

Видно, что парабола располагается ниже оси Ох на промежутке (– 1; 8). Поэтому именно этот промежуток и является ответом. Нер-во строгое, поэтому сами числа (– 1) и 8 НЕ входят в ответ, то есть для записи промежутка используются круглые скобки.

Обратите внимание: так как в исходном нер-ве используется корень нечетной (третьей) степени, то нам НЕ надо требовать, чтобы он был неотрицательным. Он может быть меньше нуля.

Теперь рассмотрим более сложный случай, когда в правой части нер-ва стоит не постоянное число, а некоторое выражение с переменной, то есть оно имеет вид

Случаи, когда n является нечетным числом, значительно более простые. В таких ситуациях достаточно возвести нер-во в нужную степень.

Пример. Решите нер-во

Решение.Слева стоит кубический корень, а возведем нер-во в третью степень (при этом мы используем формулу сокращенного умножения):

И снова квадратное нер-во. Найдем нули функции записанной слева, и отметим их на координатной прямой:

D = b 2 – 4ac = (– 1) 2 – 4•1•(– 2) = 1 + 8 = 9

Нер-во выполняется при х∈(– ∞; – 1)⋃(2; + ∞). Так как мы возводили нер-во в нечетную степень, то больше никаких действий выполнять не надо.

стоит корень четной степени, то ситуация резко осложняется. Его недостаточно просто возвести его в n-ую степень. Необходимо выполнение ещё двух условий:

f(x) > 0 (подкоренное выражение не может быть отрицательным);

g(x) > 0 (ведь сам корень должен быть неотрицательным, поэтому если g(x)будет меньше нуля, то решений не будет).

Вообще говоря, в таких случаях аналитическое решение найти возможно, но это тяжело. Поэтому есть смысл решить нер-во графически – такое решение будет более простым и наглядным.

Пример. Решите нер-во

Решение. Сначала решим его аналитически, без построения графиков. Возведя нер-во в квадрат, мы получим

х 2 – 10х + 21 > 0(1)

Решением этого квадратного нер-ва будет промежуток (– ∞;3)⋃(7; + ∞). Но надо учесть ещё два условия. Во-первых, подкоренное выражение должно быть не меньше нуля:

Во-вторых, выражение 4 – х не может быть отрицательным:

Получили ограничение 2,5 ⩽ х ⩽ 4, то есть х∈[2,5; 4]. С учетом того, что при решении нер-ва(1) мы получили х∈(– ∞;3)⋃(7; + ∞), общее решение иррационального нер-ва будет их пересечением, то есть промежутком [2,5; 3):

Скажем честно, что описанное здесь решение достаточно сложное для понимания большинства школьников, поэтому предложим альтернативное решение, основанное на использовании графиков. Построим отдельно графики левой и правой части нер-ва:

Видно, что график корня находится ниже прямой на промежутке [2,5; 3). Возникает вопрос – точно ли мы построили график? На самом деле с его помощью мы лишь определили, что искомый промежуток находится между двумя точками. В первой график корня касается оси Ох, а во второй точке он пересекается с прямой у = 4 – х. Найти координаты этих точек можно точно, если решить ур-ния. Начнем с первой точки:

Итак, координата х первой точки в точности равна 2,5. Для нахождения второй точки составим другое ур-ние:

Это квадратное ур-ние имеет корни 3 и 7 (убедитесь в этом самостоятельно). Число 7 является посторонним корнем:

Подходит только число 3, значит, вторая точка имеет координату х = 3, а искомый промежуток – это [2,5; 3).

Ещё тяжелее случаи, когда в нер-ве с корнем четной степени стоит знак «>», а не « 1/2 = х – 3

💡 Видео

Избавиться от иррациональности в знаменателе ➜ 1/(∜2+∜3)Скачать

Степень числа с иррациональным показателем. 11 класс.Скачать

Преобразование иррациональных выражений. 11 класс.Скачать

Избавиться от иррациональности в знаменателе ➜ 1/(1+√2+√3)Скачать