 Алгебраическая форма записи комплексных чисел Алгебраическая форма записи комплексных чисел |
 Сложение, вычитание и умножение комплексных чисел, записанных в алгебраической форме Сложение, вычитание и умножение комплексных чисел, записанных в алгебраической форме |
 Комплексно сопряженные числа Комплексно сопряженные числа |
 Модуль комплексного числа Модуль комплексного числа |
 Деление комплексных чисел, записанных в алгебраической форме Деление комплексных чисел, записанных в алгебраической форме |
 Изображение комплексных чисел радиус-векторами на координатной плоскости Изображение комплексных чисел радиус-векторами на координатной плоскости |
 Аргумент комплексного числа Аргумент комплексного числа |
 Тригонометрическая форма записи комплексного числа Тригонометрическая форма записи комплексного числа |
 Формула Эйлера. Экспоненциальная форма записи комплексного числа Формула Эйлера. Экспоненциальная форма записи комплексного числа |
 Умножение, деление и возведение в натуральную степень комплексных чисел, записанных в экспоненциальной форме Умножение, деление и возведение в натуральную степень комплексных чисел, записанных в экспоненциальной форме |
 Извлечение корня натуральной степени из комплексного числа Извлечение корня натуральной степени из комплексного числа |
- Алгебраическая форма записи комплексных чисел
- Сложение, вычитание и умножение комплексных чисел, записанных в алгебраической форме
- Комплексно сопряженные числа
- Модуль комплексного числа
- Деление комплексных чисел, записанных в алгебраической форме
- Изображение комплексных чисел радиус-векторами координатной плоскости
- Аргумент комплексного числа
- Формула Эйлера. Экспоненциальная форма записи комплексного числа
- Умножение, деление и возведение в натуральную степень комплексных чисел, записанных в экспоненциальной форме
- Извлечение корня натуральной степени из комплексного числа
- Комплексные числа и их приложение к решению уравнений третьей и четвертой степени (стр. 2 )
- Занятие 4. Действия с комплексными числами в алгебраической форме
- 🌟 Видео
Видео:Математика без Ху!ни. Комплексные числа, часть 1. Введение.Скачать

Алгебраическая форма записи комплексных чисел
Пусть x и y — произвольные вещественные числа.
Множеством комплексных чисел называют множество всевозможных пар (x, y) вещественных чисел, на котором определены операции сложения, вычитания и умножения по правилам, описанным чуть ниже.
Множество комплексных чисел является расширением множества вещественных чисел, поскольку множество вещественных чисел содержится в нём в виде пар (x, 0) .
Комплексные числа, заданные парами (0, y) , называют чисто мнимыми числами .
Для комплексных чисел существует несколько форм записи: алгебраическая форма записи, тригонометрическая форма записи и экспоненциальная (показательная) форма записи .
Алгебраическая форма — это такая форма записи комплексных чисел, при которой комплексное число z, заданное парой вещественных чисел (x, y) , записывается в виде
| z = x + i y . | (1) |
где использован символ i , называемый мнимой единицей .
Число x называют вещественной (реальной) частью комплексного числа z = x + i y и обозначают Re z .
Число y называют мнимой частью комплексного числа z = x + i y и обозначают Im z .
Комплексные числа, у которых Im z = 0 , являются вещественными числами .
Комплексные числа, у которых Re z = 0 , являются чисто мнимыми числами .
Тригонометрическая и экспоненциальная формы записи комплексных чисел будут изложены чуть позже.
Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Сложение, вычитание и умножение комплексных чисел, записанных в алгебраической форме
Умножение комплексных чисел z1 = x1 + i y1 и z2 = x2 + i y2 , так же, как и операции сложения и вычитания, осуществляется по правилам умножения двучленов (многочленов), однако при этом учитывается важнейшее равенство, имеющее вид:
| i 2 = – 1 . | (2) |
По этой причине
Видео:КОМПЛЕКСНЫЕ ЧИСЛА ДЛЯ ЧАЙНИКОВ ЗА 7 МИНУТСкачать

Комплексно сопряженные числа
Два комплексных числа z = x + iy и 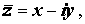
Операция перехода от комплексного числа к комплексно сопряженному с ним числу называется операцией комплексного сопряжения , обозначается горизонтальной чертой над комплексным числом и удовлетворяет следующим свойствам:
 |  |
 |  |
 |  |
 |  |
 |  |
Видео:✓ Как решать кубические уравнения. Формула Кардано | Ботай со мной #025 | Борис ТрушинСкачать

Модуль комплексного числа
Модулем комплексного числа z = x + i y называют вещественное число, обозначаемое | z | и определенное по формуле
Для произвольного комплексного числа z справедливо равенство:
а для произвольных комплексных чисел z1 и z2 справедливы неравенства:
 |  |
 |  |
 |  |
 |  |
Замечание . Если z — вещественное число, то его модуль | z | равен его абсолютной величине.
Видео:Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Деление комплексных чисел, записанных в алгебраической форме
Деление комплексного числа z1 = x1 + i y1 на отличное от нуля комплексное число z2 = x2 + i y2 осуществляется по формуле
Используя обозначения модуля комплексного числа и комплексного сопряжения, частное от деления комплексных чисел можно представить в следующем виде:
Деление на нуль запрещено.
Видео:Математика без Ху!ни. Комплексные числа, часть 3. Формы записи. Возведение в степень.Скачать

Изображение комплексных чисел радиус-векторами координатной плоскости
Рассмотрим плоскость с заданной на ней прямоугольной декартовой системой координат Oxy и напомним, что радиус-вектором на плоскости называют вектор, начало которого совпадает с началом системы координат.
Назовем рассматриваемую плоскость комплексной плоскостью , и будем представлять комплексное число z = x + i y радиус–вектором с координатами (x , y).
Назовем ось абсцисс Ox вещественной осью , а ось ординат Oy – мнимой осью .
При таком представлении комплексных чисел сумме комплексных чисел соответствует сумма радиус-векторов, а произведению комплексного числа на вещественное число соответствует произведение радиус–вектора на это число.
Видео:Найдите производную функции x^x ★ Как находить производные показательно-степенных функцийСкачать

Аргумент комплексного числа
Рассмотрим радиус–вектор произвольного, но отличного от нуля, комплексного числа z .
Аргументом комплексного числа z называют угол φ между положительным направлением вещественной оси и радиус-вектором z .
Аргумент комплексного числа z считают положительным, если поворот от положительного направления вещественной оси к радиус-вектору z происходит против часовой стрелки, и отрицательным — в случае поворота по часовой стрелке (см. рис.).
Считается, что комплексное число нуль аргумента не имеет.
Поскольку аргумент любого комплексного числа определяется с точностью до слагаемого 2kπ , где k — произвольное целое число, то вводится, главное значение аргумента , обозначаемое arg z и удовлетворяющее неравенствам:
Тогда оказывается справедливым равенство:
Если для комплексного числа z = x + i y нам известны его модуль r = | z | и его аргумент φ , то мы можем найти вещественную и мнимую части по формулам
 | (3) |
Если же комплексное число z = x + i y задано в алгебраической форме, т.е. нам известны числа x и y , то модуль этого числа, конечно же, определяется по формуле
 | (4) |
а аргумент определяется в соответствии со следующей Таблицей 1.
Для того, чтобы не загромождать запись, условимся, не оговаривая этого особо, символом k обозначать в Таблице 1 произвольное целое число.
Таблица 1. – Формулы для определения аргумента числа z = x + i y
| Расположение числа z | Знаки x и y | Главное значение аргумента | Аргумент | Примеры |
| Положительная вещественная полуось | 0 | φ = 2kπ |  | |
| Первый квадрант |  |  |  | |
| Положительная мнимая полуось |  |  |  | |
| Второй квадрант |  |  |  | |
| Отрицательная вещественная полуось | Положительная вещественная полуось | |||
| Знаки x и y | ||||
| Главное значение аргумента | 0 | |||
| Аргумент | φ = 2kπ | |||
| Примеры |  |
| Расположение числа z | Первый квадрант |
| Знаки x и y | |
| Главное значение аргумента |  |
| Аргумент |  |
| Примеры |  |
| Расположение числа z | Положительная мнимая полуось |
| Знаки x и y | |
| Главное значение аргумента |  |
| Аргумент |  |
| Примеры |  |
| Расположение числа z | Второй квадрант |
| Знаки x и y | |
| Главное значение аргумента |  |
| Аргумент |  |
| Примеры |  |
| Расположение числа z | Отрицательная вещественная полуось | |||||||||||||
| Знаки x и y | Третий квадрант | |||||||||||||
| Знаки x и y | Отрицательная мнимая полуось | |||||||||||||
| Знаки x и y | Четвёртый квадрант | |||||||||||||
| Знаки x и y | ||||||||||||||
| z = r (cos φ + i sin φ) , | (5) |
где r и φ — модуль и аргумент этого числа, соответственно, причем модуль удовлетворяет неравенству r > 0 .
Запись комплексного числа в форме (5) называют тригонометрической формой записи комплексного числа .
Видео:Комплексные числа и "золотое" уравнениеСкачать

Формула Эйлера. Экспоненциальная форма записи комплексного числа
В курсе «Теория функций комплексного переменного», который студенты изучают в высших учебных заведениях, доказывается важная формула, называемая формулой Эйлера :
| cos φ + i sin φ = e iφ . | (6) |
Из формулы Эйлера (6) и тригонометрической формы записи комплексного числа (5) вытекает, что любое отличное от нуля комплексное число z = x + i y может быть записано в виде
| z = r e iφ , | (7) |
где r и φ — модуль и аргумент этого числа, соответственно, причем модуль удовлетворяет неравенству r > 0 .
Запись комплексного числа в форме (7) называют экспоненциальной (показательной) формой записи комплексного числа .
Из формулы (7) вытекают, в частности, следующие равенства:
а из формул (4) и (6) следует, что модуль комплексного числа
или, что то же самое, числа e iφ , при любом значении φ равен 1.
Видео:Диофантовы уравнения x+y=xyСкачать

Умножение, деление и возведение в натуральную степень комплексных чисел, записанных в экспоненциальной форме
Экспоненциальная запись комплексного числа очень удобна для выполнения операций умножения, деления и возведения в натуральную степень комплексных чисел.
Действительно, умножение и деление двух произвольных комплексных чисел 

Таким образом, при перемножении комплексных чисел их модули перемножаются, а аргументы складываются.
При делении двух комплексных чисел модуль их частного равен частному их модулей, а аргумент частного равен разности аргументов делимого и делителя.
Возведение комплексного числа z = r e iφ в натуральную степень осуществляется по формуле
Другими словами, при возведении комплексного числа в степень, являющуюся натуральным числом, модуль числа возводится в эту степень, а аргумент умножается на показатель степени.
Видео:10 класс, 32 урок, Комплексные числа и арифметические операции над нимиСкачать

Извлечение корня натуральной степени из комплексного числа
Пусть 
Корнем n — ой степени из числа z0 , где 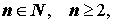
| z n = z0 . | (8) |
Для того, чтобы решить уравнение (8), перепишем его в виде
и заметим, что два комплексных числа, записанных в экспоненциальной форме, равны тогда и только тогда, когда их модули равны, а разность аргументов равна 2kπ , где k — произвольное целое число. По этой причине справедливы равенства
следствием которых являются равенства
 | (9) |
Из формул (9) вытекает, что уравнение (8) имеет n различных корней
 | (10) |
причем на комплексной плоскости концы радиус-векторов zk при k = 0 , . , n – 1 располагаются в вершинах правильного n — угольника, вписанного в окружность радиуса 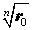
Замечание . В случае n = 2 уравнение (8) имеет два различных корня z1 и z2 , отличающихся знаком:
Пример 1 . Найти все корни уравнения
то по формуле (10) получаем:
Пример 2 . Решить уравнение
Решение . Поскольку дискриминант этого квадратного уравнения отрицателен, то вещественных корней оно не имеет. Для того, чтобы найти комплексные корни, выделим, как и в вещественном случае, полный квадрат:
Видео:10 класс, 35 урок, Комплексные числа и квадратные уравненияСкачать

Комплексные числа и их приложение к решению уравнений третьей и четвертой степени (стр. 2 )
 | Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 |
Решение. Комплексные числа z1 = (х − 4) + (у2 + 5) и z2 = (у2 + 1) − 3xi будут противоположными, если выполняются условия:
Решая полученную систему, находим :
Задача 10. При каких действительных значениях х и у комплексные числа z1 = 2x2 – yi −1− 
Решение. Комплексные числа z1= (2х2 –1)+ (3 – y)i, z2 = (у–3) + (х2–2)i будут равными, если выполняются условия:
Решая систему, находим:
Ответ : (-1 ; 4) ; (1 ; 4) .
Видео:Математика без Ху!ни. Комплексные числа, часть 2. Простейшие действия.Скачать

Занятие 4. Действия с комплексными числами в алгебраической форме
Задача 1. Произведите действия с комплексными числами в алгебраической форме:
а) 
в) 
Ответ: a) 2 + i ; б) 
Задача 2. Решите уравнения относительно действительных переменных х и у:
б)
Ответ: a) 
б) (1;3); (-1;-3);
Задача 3. Найдите значения следующих многочленов:
б) 2x3 + 3 

у = 
Ответ: а) 1 ; б) 2 ; в) 6 + 6i .
Замечание. В примерах б) и в) необходимо сначала свернуть формулы куба суммы и куба разности соответственно.
Задача 4. Вычислите следующие квадратные корни:
а) 

Ответ: а) 

Задача 5. Решите квадратные уравнения:
Ответ: а) –2 + i ; –3 + i ; в) 1 – i ; 0,8 – 0,4 i ;
Задача 6. Найдите все комплексные числа, каждое из которых сопряжено с самим собой.
Ответ: множество действительных чисел R .
Задача 7. Как связаны между собой два комплексных числа, сумма и произведение которых являются действительными числами?
Ответ: эти числа либо оба действительные, либо сопряжены друг другу.
Задача 8. Найдите все комплексные числа, сопряженные своему кубу.
Занятие 5. Контрольная работа №1
1. Вычислите: 
2. Вычислите двумя способами квадратный: 
3. Решите уравнение: (4 + 3i)2 х + (4 − 3i)2 у = − 7 + 120 i,
считая х и у действительными числами.
4. Решите квадратное уравнение:
5. Зная, что x1 = 2i является корнем кубического уравнения х3 – 3х2 + 4х – 12 = 0, найдите остальные корни данного уравнения.
Глава 2. ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ
КОМПЛЕКСНЫХ ЧИСЕЛ
Занятие 6. Геометрическая интерпретация комплексных чисел
Введем на плоскости прямоугольную
систему координат хОу и поставим в
соответствие каждому комплексному
числу z = а + bi точку плоскости с
координатами (а;b). Полученное
соответствие между всеми



соответствует одна точка плоскости с
координатами (а;b) , и обратно, каждой
точке плоскости с координатами (а;b)
комплексное число z = а + bi (см. рис. 1).
Таким образом, через z мы будем одновременно обозначать и комплексное число и точку, изображающую это комплексное число.
Комплексное число z=а+bi называется комплексной координатой точки (а;b) .
Поскольку при указанном соответствии действительные числа z = а + 0i изображаются точками оси абсцисс, то ось Ох называется действительной осью. Ось Oу , на которой лежат чисто мнимые числа z = 0 + bi, называется мнимой осью. Плоскость, точки которой изображают комплексные числа, называется комплексной плоскостью.
Комплексное число z = а + bi может также изображаться вектором с координатами а и b , идущим из начала координат в точку (а;b) (см. рис.1).
Поскольку по определению модуля комплексного числа

очевидно, что модуль комплексного числа равен длине вектора 
Рассмотрим произвольный вектор 


Вектору 

Таким образом, мы приходим к следующему определению: комплексной координатой вектора называется комплексное число z = a + bi .
🌟 Видео
Комплексные корни квадратного уравненияСкачать

Комплексные числа в уравненияхСкачать

Математика это не ИсламСкачать

Сложение, вычитание, умножение и деление комплексных чисел | Высшая математикаСкачать

МЕТОД ПОДСТАНОВКИ 😉 СИСТЕМЫ УРАВНЕНИЙ ЧАСТЬ I#математика #егэ #огэ #shorts #профильныйегэСкачать

Комплексные числа #1Скачать

Тригонометрическая форма комплексного числаСкачать

ТФКП. Найти действительную и мнимую часть функции комплексного переменного f(z), z=x+iyСкачать



































