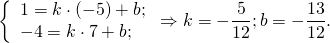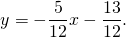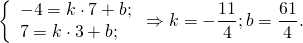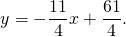Как составить уравнение сторон треугольника по координатам его вершин?
Зная координаты вершин треугольника, можно составить уравнение прямой, проходящей через 2 точки.
Дано: ΔABC, A(-5;1), B(7;-4), C(3;7)
Составить уравнения сторон треугольника.
1) Составим уравнение прямой AB, проходящей через 2 точки A и B.
Для этого в уравнение прямой y=kx+b подставляем координаты точек A(-5;1), B(7;-4) и из полученной системы уравнений находим k и b:
Таким образом, уравнение стороны AB
2) Прямая BC проходит через точки B(7;-4) и C(3;7):
Отсюда уравнение стороны BC —
3) Прямая AC проходит через точки A(-5;1) и C(3;7):
- Решить треугольник Онлайн по координатам
- Уравнение прямой
- Уравнение прямой на плоскости
- Уравнение прямой с угловым коэффициентом
- Уравнение прямой в отрезках на осях
- Уравнение прямой, проходящей через две различные точки на плоскости
- Параметрическое уравнение прямой на плоскости
- Каноническое уравнение прямой на плоскости
- Уравнение прямой в пространстве
- Уравнение прямой, проходящей через две различные точки в пространстве
- Параметрическое уравнение прямой в пространстве
- Каноническое уравнение прямой в пространстве
- Прямая как линия пересечения двух плоскостей
- 💡 Видео
Видео:найти уравнение высоты треугольникаСкачать
Решить треугольник Онлайн по координатам
1) длины и уравнения сторон, медиан, средних линий, высот, серединных перпендикуляров, биссектрис;
2) система линейных неравенств, определяющих треугольник;
2) уравнения прямых, проходящих через вершины параллельно противолежащим сторонам;
3) внутренние углы по теореме косинусов;
4) площадь треугольника;
5) точка пересечения медиан (центроид) и точки пересечения медиан со сторонами;
10) параметры вписанной и описанной окружностей и их уравнения.
Внимание! Этот сервис не работает в браузере IE (Internet Explorer).
Запишите координаты вершин треугольника и нажмите кнопку.
| A ( ; ), B ( ; ), C ( ; ) | Примечание: дробные числа записывайте Округлять до -го знака после запятой. Видео:Уравнение прямой и треугольник. Задача про высотуСкачать  Уравнение прямой
Видео:Уравнения стороны треугольника и медианыСкачать  Уравнение прямой на плоскостиЛюбую прямую на плоскости можно задать уравнением прямой первой степени вида где A и B не могут быть одновременно равны нулю.
Уравнение прямой с угловым коэффициентомОбщее уравнение прямой при B≠0 можно привести к виду где k — угловой коэффициент равный тангенсу угла, образованного данной прямой и положительным направлением оси ОХ.
Уравнение прямой в отрезках на осяхЕсли прямая пересекает оси OX и OY в точках с координатами ( a , 0) и (0, b ), то она может быть найдена используя формулу уравнения прямой в отрезках
Уравнение прямой, проходящей через две различные точки на плоскостиЕсли прямая проходит через две точки M( x 1, y 1) и N( x 2, y 2), такие что x 1 ≠ x 2 и y 1 ≠ y 2, то уравнение прямой можно найти, используя следующую формулу
Параметрическое уравнение прямой на плоскостиПараметрические уравнения прямой могут быть записаны следующим образом x = l t + x 0 y = m t + y 0 где N( x 0, y 0) — координаты точки лежащей на прямой, a = — координаты направляющего вектора прямой. Каноническое уравнение прямой на плоскостиЕсли известны координаты точки N( x 0, y 0) лежащей на прямой и направляющего вектора a = ( l и m не равны нулю), то уравнение прямой можно записать в каноническом виде, используя следующую формулу
Решение. Воспользуемся формулой для уравнения прямой проходящей через две точки x — 1 2 — 1 = y — 7 3 — 7 Упростив это уравнение получим каноническое уравнение прямой Выразим y через x и получим уравнение прямой с угловым коэффициентом Найдем параметрическое уравнение прямой. В качестве направляющего вектора можно взять вектор MN . Взяв в качестве координат точки лежащей на прямой, координаты точки М, запишем параметрическое уравнение прямой x = t + 1 y = -4 t + 7 Решение. Так как M y — N y = 0, то невозможно записать уравнение прямой проходящей через две точки. Найдем параметрическое уравнение прямой. В качестве направляющего вектора можно взять вектор MN . Взяв в качестве координат точки лежащей на прямой, координаты точки М, запишем параметрическое уравнение прямой Видео:найти уравнения биссектрис углов между прямымиСкачать  Уравнение прямой в пространствеУравнение прямой, проходящей через две различные точки в пространствеЕсли прямая проходит через две точки M( x 1, y 1, z 1) и N( x 2, y 2, z 2), такие что x 1 ≠ x 2, y 1 ≠ y 2 и z 1 ≠ z 2, то уравнение прямой можно найти используя следующую формулу
Параметрическое уравнение прямой в пространствеПараметрические уравнения прямой могут быть записаны следующим образом
где ( x 0, y 0, z 0) — координаты точки лежащей на прямой, — координаты направляющего вектора прямой. Каноническое уравнение прямой в пространствеЕсли известны координаты точки M( x 0, y 0, z 0) лежащей на прямой и направляющего вектора n = , то уравнение прямой можно записать в каноническом виде, используя следующую формулу
Прямая как линия пересечения двух плоскостейЕсли прямая является пересечением двух плоскостей, то ее уравнение можно задать следующей системой уравнений 💡 ВидеоМатематика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать  №973. Даны координаты вершин треугольника ABC: А (4; 6), В (-4; 0), С (-1; -4). Напишите уравнениеСкачать  Вычисляем высоту через координаты вершин 1Скачать  Аналитическая геометрия, 6 урок, Уравнение прямойСкачать  9 класс, 7 урок, Уравнение прямойСкачать  Уравнение прямой и треугольник. Задача про медиануСкачать  Вычисление медианы, высоты и угла по координатам вершинСкачать  Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать  Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать  Уравнение прямой по двум точкамСкачать  Уравнения прямой на плоскости | Векторная алгебраСкачать  Уравнение прямой и треугольник. Задача про сторонуСкачать  Задача по геометрии на прямоугольный треугольник и теорему Пифагора из реального ОГЭ по математикеСкачать  Аналитическая геометрия на плоскости. Решение задачСкачать  Высшая математика. 3 урок. Аналитическая геометрия. Вычисление площади треугольникаСкачать  Аналитическая геометрия на плоскостиСкачать  | ||||||||||||||||||||||||||||||||||||||
