Как найти уравнение перпендикуляра опущенного из вершины а4 на грань а1а2а3

Если я правильно понял, то все вершины заданы координатами.
Как вариант, такое решение:
1. Запишите уравнение плоскости А1А2А3.
2. Найдите вектор нормали.
3. Зная точку и направляющий вектор (он же вектор нормали к плоскости) напишите уравнение прямой.

Второй вариант.
1. Запишите вектора А1А2 и А2А3.
2. Найдите их векторное произведение.
3. Зная точку и направляющий вектор (он же вектор, из п.2) напишите уравнение прямой.

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Примеры решений по аналитической геометрии в пространстве

В этом разделе вы найдете бесплатные примеры решений задач по аналитической геометрии в пространстве, которые относятся к исследованию пирамиды. Обычно в такой задаче нужно найти длины ребер, углы между ребрами, уравнения граней пирамиды и их площади, объем пирамиды, угол между ребром и гранью, уравнение высоты, длину высоты пирамиды и т.д.

Видео:Записать уравнение прямой параллельной или перпендикулярной данной.Скачать

Решения задачи о пирамиде онлайн

Задача 1. Для пирамиды с вершинами в точках $A_1, A_2, A_3, A_4$ найти:
А) длину ребра $A_1A_2$;
Б) угол между ребрами $A_1A_2$ и $A_1A_4$;
В) уравнение плоскости $A_1A_2A_3$;
Г) площадь грани $A_1A_2A_3$;
Д) угол между ребрами $A_1A_4$ и плоскостью $A_1A_2A_3$;
Е) уравнение высоты, опущенной из точки $A_4$ на грань $A_1A_2A_3$;
Ж) объем пирамиды $A_1A_2A_3A_4$.

Задача 2. Даны координаты вершин пирамиды $$A(12;11;17), B(14;12;14), C(13;14;15), D(12;21;12).$$ Найти:
— объем пирамиды;
— площадь грани $ABC$;
— уравнение плоскости, проходящей через точки $B,C,D$;
— длину высоты пирамиды, опущенной на грань $ABC$.

Задача 3. Пирамида $АВСD$ задана координатами своих вершин: $$А(4, -1,0), B(2, 3, 4), C(-1, 4, 1), D(4, -3, 5).$$ Найдите:
1. угол между ребрами $АВ$ и $АС$,
2. уравнение ребра $АВ$,
3. уравнение грани $АВС$,
4. уравнение высоты, опущенной из вершины $D$, на грань $АВС$,
5. выясните, образуют ли векторы $АВ, АС, АD$ линейно независимую систему,
6. координаты вектора $MN$, если $М$ – середина ребра $AD$, $N$ – середина ребра $ВC$,
7. разложите вектор $MN$ по базису $AB, AC, AD$, если он таковым является.

Видео:Уравнения стороны треугольника и медианыСкачать

Уравнение прямой а4м перпендикулярной к плоскости а1а2а3

С помощю этого онлайн калькулятора можно построить уравнение прямой, проходящей через данную точку и перпендикуляной данной плоскости. Дается подробное решение с пояснениями. Для построения уравнения прямой введите координаты точки и коэффициенты уравнения плоскости в ячейки и нажимайте на кнопку «Решить».

Предупреждение

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

Видео:Уравнения прямой на плоскости | Векторная алгебраСкачать

Уравнение прямой, проходящей через данную точку и перпендикулярной данной плоскости

Наша цель построить уравнение прямой, проходящей через данную точку M и перпендикулярной к данной плоскости Ax+By+Cz+D=0.

Общее уравнение плоскости имеет вид:

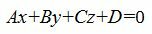(1)

где n(A,B,C)− называется нормальным вектором плоскости.

Уравнение прямой, проходящей через точку M (x , y , z ) и имеющий направляющий вектор q(l, m, n) имеет следующий вид:

(2)

Для того, чтобы прямая (2) была ортогональна плоскости (1), направляющий вектор q(l, m, n) прямой (2) должен быть коллинеарным нормальному вектору n(A,B,C) плоскости (1)(Рис. 1). Следовательно, в качестве направляющего вектора прямой (2) можно взять нормальный вектор плоскости (1) .

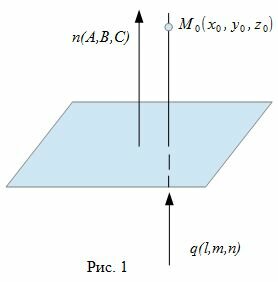Таким образом, уравнение прямой, проходящей через точку M (x , y , z ) и ортогональный плоскости (1) имеет следующий вид:

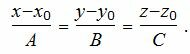(3)

Пример 1. Построить прямую, проходящую через точку M (5, -4, 4) и перпендикулярной плоскости

Общее уравнение плоскости имеет вид (1), где :

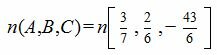(4)

Подставляя координаты точки M (5, -4, 4) и координаты нормального вектора плоскости (4) в (3), получим:

Что ты хочешь узнать?

Видео:1. Уравнение плоскости проходящей через точку перпендикулярно вектору / общее уравнение / примерыСкачать

Ответ

Проверено экспертом

Даны координаты пирамиды: A1(6,8,2), A2(5,4,7), A3(2,4,7), A4(7,3,7).
1) Координаты векторов.
Координаты векторов находим по формуле:
X = xj — xi; Y = yj — yi; Z = zj — zi
здесь X,Y,Z координаты вектора; xi, yi, zi — координаты точки Аi; xj, yj, zj — координаты точки Аj;
Например, для вектора A1A2
X = x2 — x1; Y = y2 — y1; Z = z2 — z1
X = 5-6; Y = 4-8; Z = 7-2
A1A2(-1;-4;5)
A1A3(-4;-4;5)
A1A4(1;-5;5)
A2A3(-3;0;0)
A2A4(2;-1;0)
A3A4(5;-1;0)

2) Модули векторов (длина ребер пирамиды)
Длина вектора a(X;Y;Z) выражается через его координаты формулой:
a = √(X² + Y² + Z²).
Нахождение длин ребер и координат векторов.
Вектор А1A2= -1 -4 5 L = 6,480740698.
Вектор A2A3= -3 0 0 L =3.
Вектор А1A3= -4 -4 5 L = 7,549834435.
Вектор А1A4= 1 -5 5 L =7,141428429.
Вектор A2A4= 2 -1 0 L = 2,236067977.
Вектор A3A4= 5 -1 0 L = 5,099019514.

3) Уравнение прямой
Прямая, проходящая через точки A1(x1; y1; z1) и A2(x2; y2; z2), представляется уравнениями:

Параметрическое уравнение прямой:
x=x ₀ +lt
y=y ₀ +mt
z=z ₀ +nt
Уравнение прямой A1A2(-1,-4,5)

Параметрическое уравнение прямой:
x=6-t
y=8-4t
z=2+5t.

4) Уравнение плоскости А1А2А3.

-1 -4 5
-4 -4 5 = 0
(x-6)((-4)*5-(-4)*5) — (y-8)((-1)*5-(-4)*5) + (z-2)((-1)*(-4)-(-4)*(-4)) =
= — 15y — 12z + 144 = 0
Упростим выражение: — 5y — 4z + 48 = 0.

5) Уравнение прямой А4М, перпендикулярной к плоскости А1А2А3, — это высота из точки А4 на основание пирамиды.
Прямая, проходящая через точку M₀(x₀;y₀;z₀ ) и перпендикулярная плоскости Ax + By + Cz + D = 0 имеет направляющий вектор (A;B;C).

Уравнение плоскости A1A2A3: — 5y — 4z + 48 = 0.
Уравнение А4М:

6) Уравнение плоскости, проходящей через точку перпендикулярно вектору A1A2.
Уравнение плоскости, проходящей через точку M ₀(x₀, y₀, z₀ ) перпендикулярно вектору N = (l,m,n), имеет вид:
l(x- x ₀) + m(y- y₀) + n(z- z₀ ) = 0
Координаты точки A4(7;3;7)
Координаты вектора A1A2(-1;-4;5)
-1(x — 7) + (-4)(y — 3) + 5(z — 7) = 0
Искомое уравнение плоскости:
-x — 4y + 5z-16 = 0.

7) Уравнение прямой А3N, параллельной прямой А1А2.

Необходимая для решения точка А3(2; 4; 7) задана по условию, а направляющий вектор для искомой прямой возьмём тот же, что для прямой А1А2, так как они параллельны: n=(-1;-4;5).

Консультации и решение задач по алгебре, геометрии, анализу, дискретной математике.

Лучшие эксперты в этом разделе

даны четыре точки А1(1;-2;7), А2(4;2;10), А3(2;3;5), А4(5;3;7)
составить уравнение:
1). плоскости А1А2А3
2). прямой А1А2
3). прямой А4М, перпендикулярной к плоскости А1А2А3
4). прямой А3N, параллельной прямой А1А2
5) плоскости, проходящей через точку А4 перпендикулярно к прямой А1А2
вычислить:
1). площадь грани А1А2А3
2). объем пирамиды А1А2А3А4
3).угол между ребром А1А4 и гранью А1А2А3 пирамиды
4). координаты точки пересечения прямой А4М с гранью А1А2А3
угол между прямыми А1А2 и А1А3

Состояние: Консультация закрыта

Здравствуйте, Ivanob dima!
1. A₁A₂ = (3;4;3), A₁A₃ = (1;5;-2).
Чтобы найти уравнение плоскости A₁A₂A₃, вычислим определитель матрицы (по правилу треугольника)
(x-1 y+2 z-7)
(3 4 3)
(1 5 -2)
и приравняем его нулю. Получим:
A₁A₂A₃: 23x – 9y – 11z + 36 = 0.

2. Уравнение прямой, проходящей через две точки, вычисляется в одну строку:
A₁A₂: (x-1)/3 = (y+2)/4 = (z-7)/3.

3. Т.к. A₄M ⊥ A₁A₂A₃, то нормальный вектор (23;-9;-11) плоскости будет направляющим вектором прямой.
A₄M: (x-5)/23 = (y-3)/(-9) = (z-7)/(-11).

4. Т.к. прямые A₃N и A₁A₂ параллельны, то у них общий направляющий вектор A₁A₂ = (3;4;3).
A₃N: (x-2)/3 = (y-3)/4 = (z-5)/3.

5. Т.к. искомая плоскость перпендикулярна прямой A₁A₂, то её нормальным вектором будет A₁A₂ = (3;4;3).
Получаем уравнение:
3(x-5) + 4(y-3) + 3(z-7) = 0,
3x + 4y + 3z – 48 = 0.

2. Объём пирамиды A₁A₂A₃A₄ равен одной шестой модуля смешанного произведения векторов A₁A₂, A₁A₃, A₁A₄. Чтобы его найти, вычислим модуль определителя матрицы,
(3 4 3)
(1 5 -2)
(4 5 0)
составленной из координат этих векторов, и разделим на шесть:
V = 1/6 * |3*5*0 + 4*(-2)*4 + 3*1*5 – 3*5*4 – 4*1*0 – 3*(-2)*5| = 47/6.

4. Найдём точку пересечения прямой A₄M и плоскости A₁A₂A₃. Решим систему уравнений
(x-5)/23 = (y-3)/(-9) = (z-7)/(-11),
23x – 9y – 11z + 36 = 0.
Ответ: (3402/731; 2292/731; 5238/731).

Консультировал: Агапов Марсель Дата отправки: 19.10.2007, 12:35

0

Отправлять сообщения
модераторам могут
только участники портала.
ВОЙТИ НА ПОРТАЛ »
регистрация »

Возможность оставлять сообщения в мини-форумах консультаций доступна только после входа в систему.
Воспользуйтесь кнопкой входа вверху страницы, если Вы зарегистрированы или пройдите простую процедуру регистрации на Портале.

Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Решение математических задач

Дана система линейных уравнений:

Доказать её совместность и решить двумя способами:

• 1) Методом Гаусса;
• 2) средствами матричного исчисления.

Докажем совместность системы. Составим расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду.

rang(A)= rang()=3по теореме Кронекера-Капелли система совместна.

1) Решим систему по формулам Крамера:

2) Решим систему средствами матричного исчисления.

Решение системы АХ=В находится по формуле:

где А -1 — матрица, обратная к матрице А.

А -1 находится по формуле:

Даны векторы а(4; 7; 8),b (9; 1; 3),c(2; -4; 1) и d(1; -13; -13) в некотором базисе. Показать, что векторы а, в, с образуют базис, и найти координаты вектора d в этом базисе.

Векторы образуют базис, если они линейно независимы. Условием линейной независимости векторов служит следующее условие: смешанное произведение векторов отлично от нуля.

Вычислим смешанное произведение векторов .

векторы линейно независимы, а значит образуют базис.

Пусть координаты вектора в базисе следующие: . Разложение вектора по базису имеет вид: . Подставим координаты векторов:

Решим систему методом Крамера:

Ответ: координаты вектора в базисе следующие: (-2;1;0).

Даны координаты вершины пирамиды А₁А₂А₃А₄:

• 1)длину ребра А₁А₂;
• 2)угол между ребрами А₁А_{2 И}А₁А₄;
• 3)угол между ребром А₁А₄ и гранью А₁А₂А₃;
• 4)площадь грани А₁А₂А₃;
• 5)объем пирамиды;
• 6)уравнение прямой А₁А₂;
• 7)уравнение плоскости А₁А₂А₃;
• 8)уравнение высоты, опущенной из вершины А₄ на грань А₁А₂А₃. Сделать чертеж.

1) Длина ребра А₁А₂ совпадает с длиной вектора

2) Угол между ребрами А₁А_{2 И} А₁А₄ найдем используя формулу скалярного произведения:

3) Угол между прямой (L) и плоскостью () Ax+By+Cz+D=0 находится по формуле:

(m;n;p)-это координаты направляющего вектора прямой А₁А₄.

Вектор является направляющим вектором прямой А₁А₄.

Для нахождения уравнения плоскости, содержащей грань А₁А₂А₃ используем уравнение плоскости, проходящей через три точки:

4) Площадь треугольника, построенного на векторах и находится по формуле:

— векторное произведение векторов

5) Площадь пирамиды, построенной на векторах , и находится по формуле:

где — смешанное произведение векторов.

6)Для нахождения уравнение прямой А₁А₂ воспользуемся каноническим уравнением прямой:

где (m;n;p) — координаты направляющего вектора прямой А₁А₂.

Вектор является направляющим вектором прямой А₁А₂.

• 7) Уравнение плоскости А₁А₂А₃:
• 8) Высота (Н), опущенная из вершины А₄ на грань А₁А₂А₃ перпендикулярна плоскости А₁А₂А₃, а значит направляющий вектор прямой Н параллелен вектору-нормали плоскости А₁А₂А₃, поэтому в качестве направляющего вектора прямой Н можно взять вектор-нормаль плоскости . Высота Н проходит через вершину А₄, поэтому можно записать каноническое уравнение высоты:

• 1)
• 2)
• 3)
• 4)
• 5)
• 6)
• 7)
• 8)

Даны уравнения одной из сторон ромба x — 3y + 10 = 0 и одной его диагоналей x + 4y — 4 = 0; диагонали ромба пересекаются в точке P(0;1). Найти уравнения остальных сторон ромба. Сделать чертеж.

Найдем точку М — точку пересечения стороны и диагонали:

Диагонали ромба точкой пересечения делятся пополам, поэтому Р(0;1) — середина отрезка MN, где M и N противоположные вершины ромба.

Запишем уравнение стороны NK, проходящей параллельно стороне (МТ):

Если прямые параллельны, то их угловые коэффициенты равны.

— уравнение прямой NK

Найдем уравнение второй диагонали ромба (ТК). Диагонали ромба перпендикулярны, поэтому их угловые коэффициенты связаны соотношением: .

• (ТК)
• (ТК)

Найдем точку Т — точку пересечения диагонали ТК и прямой МТ:

Запишем уравнение прямой ТN, используя формулу прямой, проходящей через две точки:

— уравнение стороны ТN

Сторона КМ параллельна стороне TN, поэтому угловые коэффициенты этих прямых равны.

— уравнение стороны МК

Составить уравнение и построить линию, расстояние каждой точки которой от точки А (-1; 0) вдвое меньше расстояния ее от прямой x = -4.

Пусть М(x;y) — точка, лежащая на искомой прямой.

Расстояние от точки (х₀;у₀) до прямой Ах+Ву+С=0 определяется формулой:

Расстояние от М до прямой равно:

По условию задачи , т.е.

Возведем обе части равенства в квадрат:

— уравнение искомой линии.

График полученной линии — парабола, ветви направлены вправо, вершина параболы в точке (-2,5;0), пересечение с осью ординат в точках (0;) и (0;).

Линия задана уравнением в полярной системе координат

• 1) построить линию по точкам, начиная от до и придавая значения через промежуток ;
• 2) найти уравнение данной линии в декартовой прямоугольной системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс — с полярной осью;
• 3) по уравнению в декартовой прямоугольной системе координат определить, какая это линия.

1) Построим линию по точкам, начиная от до и придавая значения через промежуток

📺 Видео

Вычисляем высоту через координаты вершин 1Скачать

Уравнение прямой и треугольник. Задача про высотуСкачать

№973. Даны координаты вершин треугольника ABC: А (4; 6), В (-4; 0), С (-1; -4). Напишите уравнениеСкачать

Уравнение плоскости через 3 точкиСкачать

Высшая математика. 4 урок. Аналитическая геометрия. Вычисление объема тетраэдра.Скачать

Математика без Ху!ни. Смешанное произведение векторовСкачать

Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать

Аналитическая геометрия, 5 урок, Уравнение плоскостиСкачать

Уравнение плоскостиСкачать

Аналитическая геометрия, 6 урок, Уравнение прямойСкачать

Прямая на плоскости. Проекция точки на прямуюСкачать

найти уравнение высоты треугольникаСкачать

4. Уравнение плоскости проходящей через три точки / в отрезках / доказательство и примерыСкачать