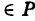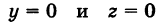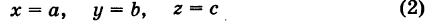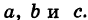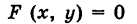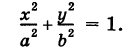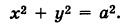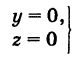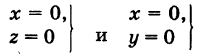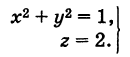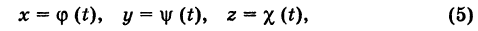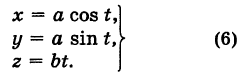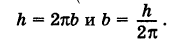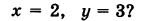Как найти уравнение границ области (7 видео)

Построение областей устойчивости. Понятие о D-разбиении

Содержание

Страницы работы
Содержание работы
Как найти уравнение границ области
Уравнения поверхности и линии в пространстве с примерами решения
Уравнения поверхности и линии в пространстве
🌟 Видео

Страницы работы

Содержание работы

Лекция 15.Построение областей устойчивости. Понятие о D—разбиении

Построение областей устойчивости и D—разбиение используются для исследования влияния значений параметров системы на ее устойчивость и качество.

Областью устойчивости в пространстве параметров системы (коэффициентов передачи, постоянных времени звеньев системы и др.) называется область значений параметров, при которых система является устойчивой.

Границы области устойчивости соответствуют границам устойчивости системы:

— апериодической (наличие нулевого корня характеристического полинома), получаемой по условию равенства нулю свободного члена характеристического полинома, a_n=0;

— соответствующей бесконечному корню характеристического полинома, получаемой по условию a₀=0;

— колебательной (наличие пары мнимых корней характеристического полинома), получаемой из условий D_n_-1=0 в соответствии с критерием Гурвица, D(jw)=0 в соответствии с критерием Михайлова или W(jw)=—1 в соответствии с критерием Найквиста.

Практический интерес представляет построение области устойчивости в плоскости двух параметров, выбираемых из множества параметров системы в соответствии с особенностями решаемых задач. Основной способ ее построения предполагает использование критерия устойчивости Михайлова.

Вводится система координат 0AB, где по осям откладываются значения параметров системы А и В.

Коэффициенты характеристического полинома замкнутой системы

выражаются через значения этих параметров.

Для получения уравнений границ области устойчивости составляются уравнения в соответствии с перечисленными выше условиями.

Основная трудоемкость при построении области устойчивости связана с построением кривой, соответствующей колебательной границе устойчивости. В соответствии с критерием Михайлова для ее получения составляется система уравнений:

, где X и Y– вещественная и мнимая части характеристического комплекса D(jw). Ее решение позволяет получить параметрические уравнения искомой кривой в форме A=A(w), B=B(w). Исключением из этих уравнений частоты можно получить уравнение в обычной форме B=B(A).

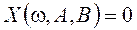
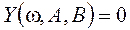
После нахождения границ области устойчивости определяется ее местонахождение. Для границ первого и третьего вида это можно сделать непосредственно на основе необходимого условия устойчивости. В области устойчивости должно иметь место a₀>0 и a_n>0.

Для колебательной границы рассматривается дополнительный критерий. Составляется определитель из частных производных

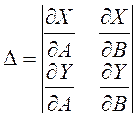
Если D>0, то при движении вдоль этой границы в направлении увеличения частоты область устойчивости расположена слева. Если D 3 +(T₁+T₂)s 2 +s+k

и характеристический комплекс

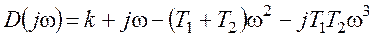
Найдем границы устойчивости.

1. Апериодическая граница: a_n=k=0. Области устойчивости соответствует k>0.

2. Граница, соответствующая бесконечному корню: a₀=T₁T₂=0. В результате уравнение границы T₁=0. Области устойчивости соответствует T₁>0.

3. Колебательная граница:

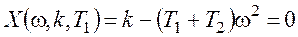
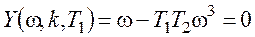
В результате получим параметрические уравнения колебательной границы:

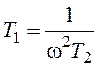
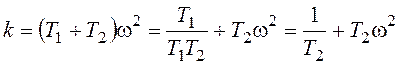
Теперь исключим из полученных уравнений частоту:

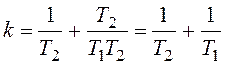
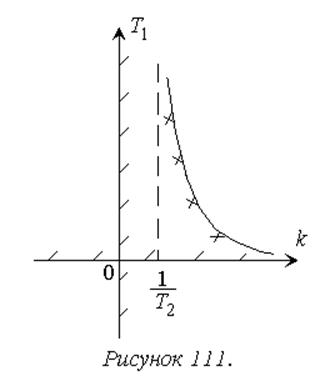
Соответствующая кривая имеет вид гиперболы (рисунок 111).

Найдем расположение области устойчивости относительно этой границы с учетом A=k, B=T₁:

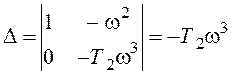
При w>0 увеличению частоты от 0 до ∞ соответствует движение по колебательной границе, как следует из параметрических уравнений, в направлении увеличения k и уменьшения T₁. При этом D 0, то есть область устойчивости расположена справа.

D—разбиением называется полная совокупность кривых, разбивающих плоскость параметров на области с различным распределением корней характеристического полинома D(s).

Видео:Математический анализ, 15 урок, АссимптотыСкачать

Как найти уравнение границ области

Изменение параметров САУ, например, с целью оптимизации, приведет к изменению коэффициентов уравнения динамики. Останется ли при этом САУ устойчивой — неизвестно. Критерии устойчивости об этом ничего не говорят. Рассмотрим метод определения границ допустимых изменений параметров, при которых САУ не теряет устойчивости.

Приведем характеристическое уравнение замкнутой САУ к виду:

D(p) = p n + c 1 p n -1 + c 2 p n-2 + . + c n = 0,

где c 0 = a 0 /a 0 = 1 , c 1 = a 1 /a 0 и т.д. При некоторых конкретных значениях c 1 ,c 2 . c n уравнение имеет единственное решение, то есть единственный набор корней ( p 1 , p 2 . p _n ). По их расположению на комплексной плоскости можно судить об устойчивости САУ при заданных параметрах. Если изменить какой-либо параметр САУ, например коэффициента передачи, то изменятся и коэффициенты характеристического уравнения D(p) = 0 и станут равными c н1 ,c н2 . c нn . Уравнение примет вид:

D _н (p) = p n + c н1 p n -1 + c н2 p n -2 + . + c нn = 0.

Это уже другое уравнение и оно также имеет единственное решение (p н1 ,p н2 . p нn ) , отличающееся от (p 1 ,p 2 . p n ) . Если плавно менять значение параметра САУ, то коэффициенты уравнения тоже будут плавно изменяться, а его корни будут перемещаться по комплексной плоскости (рис.81).

Каждый уникальный набору коэффициентов c 1 ,c 2 . c n можно изобразить точкой в пространстве коэффициентов, по осям которого откладываются значения коэффициентов c 1 ,c 2 . c n . Так уравнению третьей степени соответствует трехмерное пространство коэффициентов (рис.82).

Пусть точка N с координатами (c _N1 ,c _N2 ,c _N3 ) соответствует уравнению, имеющему решение (p _N1 ,p _N2 ,p _N3 ) , точка M с координатами (c _M1 ,c _M2 ,c _M3 ) соответствует уравнению, имеющему решение (p M1 ,p M2 ,p M3 ) . При изменении какого-либо параметра САУ коэффициенты характеристического уравнения будут изменяться, при этом точка в пространстве коэффициентов, соответствующая данному уравнению будет перемещаться по некоторой траектории, например из положения N в положение M . Этому перемещению будет соответствовать и перемещение корней (p N1 ,p N2 ,p N3 ) на комплексной плоскости в положение (p M1 ,p M2 ,p M3 ) (аналогично рис.81).

При этом движении некоторые корни будут переходить через мнимую ось комплексной плоскости из левой полуплоскости в правую и наоборот. В момент перехода такой k -й корень примет значение p _K = j _K , а коэффициенты уравнения будут иметь определенные значения c _K1 ,c _K2 ,c _K3 , определяющие в пространстве коэффициентов точку K . Подставим корень p _K в характеристическое уравнение, получим тождество:

D(p _K ) = (j K ) 3 + cK1(j K ) 2 + c _K2 (jK ) + c _K3 = 0

Меняя w от — до + , и находя при каждой частоте все возможные сочетания коэффициентов c 1 ,c 2 . c n , удовлетворяющих уравнению

D(j ) = (j) n + c 1 (j) n-1 + c 2 (j ) n-2 + . + c n = 0,

можно построить в n -мерном пространстве коэффициентов сложную поверхность S , разделяющую его на области, называемое D -областями . Полученное уравнение называется уравнением границы D -разбиения.

Переход из одной D -области в другую через поверхность S соответствует переходу одного или нескольких корней через мнимую ось в плоскости корней. То есть каждая точка внутри определенной D -области соответствует уравнению с определенным количеством левых и правых корней. Поэтому области обозначают D(m) по числу m правых корней.

Достаточно взять любую точку в пространстве коэффициентов и найти для нее число правых корней. Затем, двигаясь по пространству коэффициентов через границу S , можно выявить обозначения всех других областей. Особый интерес представляет область D(0) , которой соответствуют уравнения с полным отсутствием правых корней, называемая областью устойчивости . Описанный метод определения областей устойчивости называется методом D -разбиений .

Не обязательно строить сложную n -мерную картину D -разбиения, можно изменять значения, например, только двух коэффициентов, оставляя другие коэффициенты постоянными. Границу D -разбиения S можно строить не только также и в пространстве конкретных параметров системы, от которых зависят данные коэффициенты.

11.2. D-разбиение по одному параметру

Пусть необходимо выявить влияние на устойчивоять САУ, например, коэффициента усиления K . Приведем характеристическое уравнение к виду D(p) = S(p) + KN(p) , выделив члены, не зависящие от K в полином S(p) , а в остальных членах, линейно зависящих от K , вынесем его за скобки. Граница D -разбиения задается уравнением

D(j ) = S(j ) + KN(j ) = 0, => K = -S(j )/N(j) = X() + jY().

Изменяя w от — до + , будем вычислять X() и Y() и по ним строить точки границы D -разбиения. Пространство коэффициентов представляется системой координат X-Y (рис.83а). Обычно строят только половину кривой ( = [0, + ), другую половину достраивают симметрично относительно вещественной оси.

Если в плоскости корней двигаться вдоль мнимой оси от — до + и штриховать ее слева (рис.83б), то это будет соответствовать движению вдоль линии D -разбиения при изменении w от — до + и штриховке ее также слева. Переходу корня в плоскости корней из штрихованной полуплоскости в нештрихованную вдоль стрелки 1 соответствует аналогичный переход через границу D -разбиения вдоль стрелки 1 , и наоборот. Если пересекается область с двойной штриховкой (точки A, В, C ), то в плоскости корней мнимую ось пересекает пара комплексно сопряженных корней.

Если известно количество правых корней, соответствующее хотя бы одной D -области, то двигаясь от нее через границы с учетом штриховок, можно обозначить все остальные области. Область с наибольшим количеством штриховок является претендентом на область устойчивости. Нужно взять любую точку из этой области и при соответствующем значении K проверить систему на устойчивость любым методом.

Есть одна особенность. Так как K — вещественное число, то Y() = 0, поэтому нас интересует не вся область устойчивости, а лишь отрезок вещественной оси в этой области, то есть K = X() .

11.3. Прямые методы оценки качества управления

Устойчивость САУ является необходимым, но не достаточным условием для ее эффективного функционирования. Важное значение имеет качество управления , то есть степень удовлетворения совокупности требований к форме кривой переходного процесса, которая определяет пригодность системы для конкретных условий работы.

Для сравнения качества различных САУ исследуется их реакция на типовые воздействия. Обычно это ступенчатая (толчковая) функция, как один из наиболее неблагоприятных видов возмущений. Для систем, работающих с периодическими возмущениями, целесообразно оценивать качество управления при гармоническом воздействии. Все остальные возмущения можно разложить на ступенчатые воздействия с использованием интеграла Дюамеля, либо в ряд Фурье.

Все современные методы анализа качества управления можно разделить на прямые методы анализа по кривой переходного процесса или по частотным характеристикам, и косвенные методы , позволяющие, не решая дифференциального уравнения, определить некоторые показатели качества процесса управления; к ним, в частности, относятся корневые, интегральные и частотные методы.

11.3.1. Оценка переходного процесса при ступенчатом воздействии.

Пусть САР (рис.84) при t = 0 воздействует возмущающий фактор f в виде единичной ступенчатой функции. При нулевых начальных условиях динамический режим описывается переходной характеристикой h(t) = y(t) = y(t) — y ₀ = -e(t) (рис.85). По ней можно определить все наиболее важные показатели качества управления.

1. Статическая ошибка e_уст = y ₀ — y уст = -h_уст — это разность между предписанным и действительным значением управляемой величины в установившемся режиме. Для статических систем статическая ошибка отлична от нуля (рис.85а) и пропорциональна величине возмущающего фактора f (в линейных САУ) и коэффициенту передачи системы по данному возмущению, а для астатических — равна нулю (рис.85б).

2. Время переходного процесса t_пп — это время от момента воздействия, начиная с которого колебания управляемой величины не превышают некоторого наперед заданного значения, то есть |h(t)-h_уст| . Обычно принимают = 0.05h_уст .

3. Перерегулирование s — это максимальное отклонение управляемой величины от установившегося значения, выраженное в относительных единицах: s = . Здесь h_{max 1} — значение первого максимума переходной характеристики. При больших перерегулированиях могут возникнуть значительные динамические усилия в механической части системы, электрические перенапряжения и т.п. Допустимое значение s определяется из опыта эксплуатации. обычно оно составляет 0.1. 0.3, иногда допускается до 0.7.

4. Частота колебаний = 2/T , где T — период колебаний.

5. Число колебаний n за время t_пп .

6. Декремент затухания k , равный отношению двух смежных перерегулирований: .

При создании САУ допустимые значения показателей качества оговариваются техническими условиями, что можно представить в виде диаграммы показателей качества . Это область, за границы которой не должна выходить переходная характеристика (рис.86).

11.3.2. Оценка качества управления при периодических возмущениях

Периодические возмущения можно разложить в ряд Фурье, поэтому их воздействие удобно анализировать по частотным характеристикам, показывающим, как звено преобразует гармонический сигнал.

Обычно используют АЧХ замкнутой САУ (рис.87), которую легко построить по АФЧХ разомкнутой САУ W _p (j ) , по формуле

Aз = .

По этой кривой можно получить ряд показателей качества.

1. Показатель колебательности M — это отношение максимального значения АЧХ замкнутой САУ к ее значению при = 0 , то есть M = A_зmax()/Aз(0) . Так как

Aз(0) = 1,

при K _p >> 1 , то M A зmax () . Он характеризует склонность системы к колебаниям и не должен превышать 1.5.

2. Резонансная частота системы _p — это частота, при которой колебания проходят через систему с наибольшим усилением, а АЧХ достигает максимума.

3. Полоса пропускания системы — это интервал частот от = 0 до = ₀ , на котором выполняется условие Aз( ₀ ) 0.707. Если она высокая, то система будет воспроизводить высокочастотные помехи.

4. Частота среза ср — при которой АЧХ замкнутой САУ принимает значение, равное единице. По ней можно судить о длительности переходного процесса t_пп (1..2)2/ _ср.

5. Склонность САУ к колебаниям характеризуют также ее запасы устойчивости по модулю (допускается от 6 до 20дб) и по фазе (допускается от 30 до 60 градусов).

Как параметры САУ влияют на вид уравнения динамики?
Что происходит с корнями характеристического полинома САУ при изменении ее параметров?
Что такое пространство коэффициентов и плоскость корней?
Что такое граница D-разбиений? Как найти ее уравнение? Как ее построить?
Что такое D-области и как они нумеруются?
Что такое область устойчивости?
Как формулируется правило штриховки в случае D-разбиения по одному параметру?
Как пронумеровать D-области в случае D-разбиения по одному параметру?
Что называется качеством управления и зачем его оценивать?
Что относится к прямым оценкам качества управления?
Что называется косвенными методами оценки качества управления?
Когда используются оценки качества управления при ступенчатом воздействии, и когда при периодическом?
Перечислите прямые оценки качества управления при ступенчатом воздействии?
Перечислите прямые оценки качества управления при периодическом воздействии?
Что называется диаграммой показателей качества?

Видео:Составляем уравнение прямой по точкамСкачать

Уравнения поверхности и линии в пространстве с примерами решения

Содержание:

Видео:Функция. Область определения функции. Практическая часть. 10 класс.Скачать

Уравнения поверхности и линии в пространстве

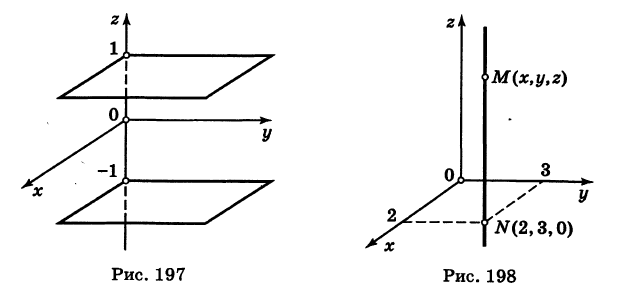
Определение: Уравнение м поверхности в пространстве Oxyz называется такое уравнение между переменными х, у у z, которому удовлетворяют координаты всех точек данной поверхности и не удовлетворяют координаты точек, не лежащих на этой поверхности. То есть если

— уравнение поверхности Р (рис. 189), то при М(х, у, z)

Таким образом, уравнение (1) выполнено тогда и только тогда, когда точка М(х, у, z) принадлежит данной поверхности. Координаты произвольной точки поверхности называются текущими координатами точки. Поэтому составить уравнение поверхности — это значит найти связь между текущими координатами ее точек.

Пример (уравнения координатных плоскостей):

Каждая точка М(х, у, z), лежащая на координатной плоскости Oyz, имеет абсциссу х = 0; обратно, если для какой-нибудь точки М(х, у, z) абсцисса ее х = 0, то эта точка расположена на плоскости Oyz. Следовательно,

— уравнение координатной плоскости Oyz. Аналогично,

— соответственно уравнения координатных плоскостей Oxz и Оху.

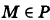
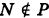
Формула обозначает, что точка М принадлежит Р. Формула обозначает, что точка N не принадлежит Р.

В более общем случае

— уравнения трех плоскостей, перпендикулярных соответствующим координатным осям Ох, Оу, Ог и отсекающих на них отрезки, численно равные

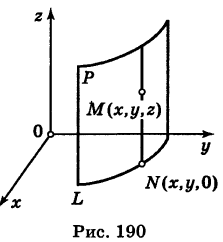
Теорема: Уравнение цилиндрической поверхности, образующие которой параллельны координатной оси, не содержит текущей координаты, одноименной с этой координатной осью, и обратно.

Доказательство: Пусть, например, цилиндрическая поверхность Р образована перемещением прямой 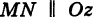(образующая) вдоль заданной линии L, лежащей в плоскости Оху (направляющая) (рис. 190).

Обозначим через М(х, у, z) точку поверхности Р с текущими координатами х, у и z. Образующая MN, проходящая через точку М, пересекает направляющую, очевидно, в точке N(x, у, 0).

— уравнение направляющей L в координатной плоскости Оху. Этому уравнению удовлетворяют координаты точки N. Так как точка М поверхности Р имеет ту же самую абсциссу хиту же самую ординату у, что и точка N, а переменная г в уравнение (3) не входит, то координаты точки М также удовлетворяют уравнению (3). Таким образом, координаты любой точки М(х, у, z) поверхности Р удовлетворяют уравнению (3). Обратно, если координаты какой-нибудь точки М(х, у, z) удовлетворяют уравнению (3), то эта точка расположена на прямой MN || Оz такой, что ее след на плоскости Оху, точка N(x, у, 0), лежит на линии L, а значит, точка М принадлежит цилиндрической поверхности Р. Следовательно,

является уравнением цилиндрической поверхности в пространстве Oxyz, причем в этом уравнении отсутствует координата z.

Пример (уравнение эллиптического цилиндра):

Эллиптический цилиндр, в основании которого лежит эллипс с полуосями а и b, а осью служит ось Оz (рис. 191), на основании предыдущей теоремы имеет уравнение

В частности, при а = b получаем уравнение кругового цилиндра

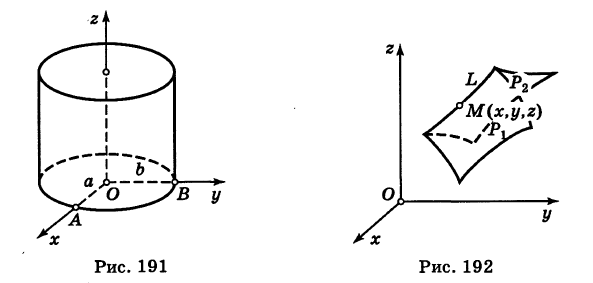
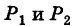
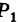
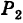
Линию L в пространстве можно задать как пересечение двух данных поверхностей (рис. 192). Точка , лежащая на линии L, принадлежит как поверхности так и поверхности , и, следовательно, координаты этой точки удовлетворяют уравнениям обеих поверхностей.

Поэтому под уравнениями линии в пространстве понимается совокупность двух уравнений:

являющихся уравнениями поверхностей, определяющих данную линию.

Не нужно думать, что для нахождения уравнений линий систему (4) следует «решить». Этого, вообще говоря, нельзя сделать, так как число уравнений системы (4) меньше числа неизвестных. Точный смысл, который придается равенствам (4), следующий: линии L принадлежат те и только те точки , координаты которых удовлетворяют обоим уравнениям системы (4).

Заметим, что данную линию можно по-разному задавать как пересечение поверхностей. Поэтому линии в пространстве соответствует бесчисленное множество равносильных между собой систем уравнений.

Определение: Уравнениями линии в пространстве называется такая пара уравнений между переменными , которой удовлетворяют координаты каждой точки, лежащей на данной линии, и не удовлетворяют координаты любой точки, не лежащей на этой линии.

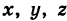
Пример (уравнения координатных осей):

Ось Ох можно, рассматривать как пересечение координатных плоскостей Оху и Oxz. Поэтому

— уравнения оси Ох. Аналогично,

— уравнения осей Оу и Oz соответственно.

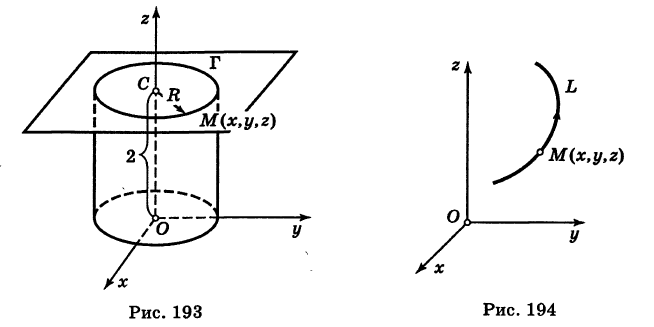
Пример:

Написать уравнения окружности Г радиуса R = 1, центр которой находится в точке С(0, 0, 2) и плоскость которой параллельна координатной плоскости Оху (рис. 193).

Решение:

Окружность Г можно рассматривать как пересечение кругового цилиндра радиуса 1 с осью Oz и горизонтальной плоскости, расположенной выше координатной плоскости Оху на две единицы. Поэтому уравнения данной окружности есть

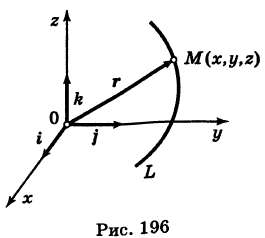
В механике линию L часто рассматривают как след движущейся точки (рис. 194). Пусть х, у, z — текущие координаты точки М линии L. Так как с течением времени точка М перемещается и ее координаты меняются, то они являются функциями времени t. Следовательно, имеем

где 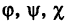— некоторые определенные функции. Обобщая уравнения (5), под t понимают вспомогательную переменную (параметр)> не обязательно время; поэтому уравнения (5) носят название параметрических уравнений линии в пространстве.

Исключая из уравнений (5) параметр t, мы получим два соотношения между текущими координатами х, у и z, которые представляют собой уравнения некоторых поверхностей, проходящих через данную линию.

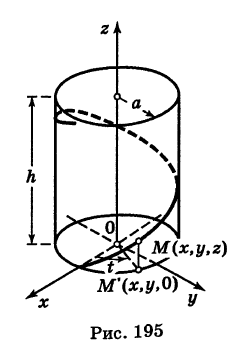
Пример:

Написать уравнения винтовой линии радиуса а и шага 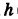(рис. 195).

Решение:

Пусть М (х, у, z) — текущая точка винтовой линии, М’ (х, у, 0) — ее проекция на плоскость Оху.

Приняв за параметр 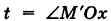и учитывая, что аппликата г винтовой линии растет пропорционально углу поворота t, будем иметь

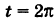
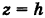
Для определения коэффициента пропорциональности b положим ; тогда . Следовательно,

Исключая параметр t из первого и второго, а также из первого и третьего уравнений (6), получаем

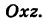
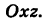
Следовательно, винтовая линия представляет собой пересечение кругового цилиндра с образующими, параллельными оси Oz, и цилиндрической поверхности с образующими, параллельными оси Оу, и имеющей своей направляющей косинусоиду, лежащую в плоскости . Из уравнений (6′) также вытекает, что проекция винтовой линии (6′) на координатную плоскость Оху есть окружность, а на координатную плоскость — косинусоида.

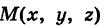
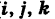
Текущую точку кривой L можно характеризовать ее радиусом-вектором («следящий радиус-вектор») (рис. 196)

( — орты). Тогда из (5) получаем векторное уравнение линии

— так называемая вектор-функция скалярного аргумента t.

В механике в качестве параметра t обычно берут время. В таком случае линию (7) называют траекторией точки М(х, у, z).

Множество всех точек М(х, у, г) пространства, координаты которых удовлетворяют данному уравнению (или системе уравнений), называется геометрическим образом (графиком) данного уравнения (или системы уравнений).

Пример:

Какой геометрический образ соответствует уравнению

Решение:

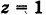
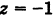
Из уравнения (8) получаем или . Следовательно, графиком уравнения (8) является пара плоскостей, параллельных координатной плоскости Оху и отстоящих от нее на расстояниях, равных единице (рис. 197).

Пример:

Какой геометрический образ соответствует паре уравнений

Решение:

Искомый график представляет собой пересечение плоскостей х = 2 и у = 3 и, следовательно, является прямой линией, параллельной оси Oz и имеющей след N (2, 3, 0) на координатной плоскости Оху (рис. 198).

Рекомендую подробно изучить предметы:

Математика
Алгебра
Линейная алгебра
Векторная алгебра
Высшая математика
Дискретная математика
Математический анализ
Математическая логика

Ещё лекции с примерами решения и объяснением:

Общее уравнение плоскости
Угол между плоскостями
Понятие о производной вектор-функции
Криволинейные интегралы
Прямоугольная система координат на плоскости и ее применение
Линии второго порядка
Полярные координаты
Непрерывность функции

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.