- Определение угла между прямыми
- Угол между прямыми на плоскости
- Угол между прямыми заданными уравнениями с угловым коэффициентом
- Угол между прямыми через направляющие векторы этих прямых
- Угол между прямыми через векторы нормалей этих прямых
- Угол между прямыми через направляющий вектор и вектор нормали этих прямых
- Примеры задач на вычисления угла между прямыми на плоскости
- Угол между прямыми в пространстве
- Угол между прямыми онлайн
- Предупреждение
- 1. Угол между прямыми на плоскости
- Прямые заданы каноническими уравнениями
- 1.1. Определение угла между прямыми
- 1.2. Условие параллельности прямых
- 1.3. Условие перпендикулярности прямых
- Прямые заданы общими уравнениями
- 1.4. Определение угла между прямыми
- 1.5. Условие параллельности прямых
- 1.6. Условие перпендикулярности прямых
- 2. Угол между прямыми в пространстве
- 2.1. Определение угла между прямыми
- 2.2. Условие параллельности прямых
- 2.3. Условие перпендикулярности прямых
- VMath
- Инструменты сайта
- Основное
- Навигация
- Информация
- Действия
- Содержание
- Длина дуги, угол между линиями, площадь области на поверхности
- Краткие теоретические сведения
- Решение задач
- Задача 1 (почти Феденко 684)
- Решение задачи 1
- Задача 2 (почти Феденко 682)
- Решение задачи 2
- Задача 3
- Решение задачи 3
- Задача 4 (Дополнение к Задаче 3)
- Задача 5 (Феденко 683)
- 📺 Видео
Видео:Видеоурок "Угол между прямыми"Скачать

Определение угла между прямыми
Видео:Угол между прямыми в пространстве. 10 класс.Скачать

Угол между прямыми на плоскости
Угол между прямыми заданными уравнениями с угловым коэффициентом
то угол между ними можно найти, используя формулу:
Если знаменатель равен нулю (1 + k 1· k 2 = 0), то прямые перпендикулярны.
Соответственно легко найти угол между прямыми
tg γ = tg ( α — β ) = tg α — tg β 1 + tg α ·tg β = k 1 — k 2 1 + k 1· k 2
Угол между прямыми через направляющие векторы этих прямых
cos φ = | a · b | | a | · | b |
Если уравнение прямой задано параметрически
x = l t + a y = m t + b
то вектор направляющей имеет вид
Если уравнение прямой задано как
то для вычисления направляющего вектора, можно взять две точки на прямой.
Например, если C ≠ 0, A ≠ 0, C ≠ 0 , при x = 0 => y = — C B значит точка на прямой имеет координаты K(0, — C B ), при y = 0 => x = — C A значит точка на прямой имеет координаты M(- C A , 0). Вектор направляющей KM = .
Если дано каноническое уравнение прямой
то вектор направляющей имеет вид
Если задано уравнение прямой с угловым коэффициентом
то для вычисления направляющего вектора, можно взять две точки на прямой, например, при x = 0 => y = b значит точка на прямой имеет координаты K(0, b ), при x = 1 => y = k + b значит точка на прямой имеет координаты M(1, k + b ). Вектор направляющей KM =
Угол между прямыми через векторы нормалей этих прямых
cos φ = | a · b | | a | · | b |
Если уравнение прямой задано как
то вектор нормали имеет вид
Если задано уравнение прямой с угловым коэффициентом
то вектор нормали имеет вид
Угол между прямыми через направляющий вектор и вектор нормали этих прямых
sin φ = | a · b | | a | · | b |
Видео:14. Угол между прямыми в пространствеСкачать

Примеры задач на вычисления угла между прямыми на плоскости
Решение: Воспользуемся формулой для вычисления угла между прямыми заданными уравнениями с угловым коэффициентом:
tg γ = k 1 — k 2 1 + k 1· k 2 = 2 — (-3) 1 + 2·(-3) = 5 -5 = 1
Решение: Воспользуемся формулой для вычисления угла между прямыми у которых известны направляющие векторы.
Для первой прямой направляющий вектор , для второй прямой направляющий вектор
cos φ = |1 · 2 + 2 · 1| 1 2 + 2 2 · 2 2 + 1 2 = 4 5 · 5 = 0.8
Решение: Для решения этой задачи можно найти направляющие векторы и вычислить угол через направляющие векторы или преобразовать уравнения в уравнения с угловым коэффициентом и вычислить угол через угловые коэффициенты.
Преобразуем имеющиеся уравнения в уравнения с угловым коэффициентом.
2 x + 3 y = 0 => y = — 2 3 x ( k 1 = — 2 3 )
x — 2 3 = y 4 => y = 4 3 x — 8 3 ( k 2 = 4 3 )
tg γ = k 1 — k 2 1 + k 1· k 2 = — 2 3 — 4 3 1 + (- 2 3 )· 4 3 = — 6 3 1 — 8 9 = 18
Видео:9. Угол между плоскостями Условия параллельности и перпендикулярности плоскостейСкачать

Угол между прямыми в пространстве
cos φ = | a · b | | a | · | b |
Если дано каноническое уравнение прямой
то направляющий вектор имеет вид
Если уравнение прямой задано параметрически
x = l t + a y = m t + b z = n t + c
то направляющий вектор имеет вид
Решение: Так как прямые заданы параметрически, то — направляющий вектор первой прямой, направляющий вектор второй прямой.
cos φ = |2 · 1 + 1 · (-2) + (-1) · 0| 2 2 + 1 2 + (-1) 2 · 1 2 + (-2) 2 + 0 2 = 0 6 · 5 = 0
Решение: Для решения этой задачи найдем направляющие векторы этих прямых.
Уравнение первой прямой задано в канонической форме, поэтому направляющий вектор .
Преобразуем второе уравнение к каноническому вид.
1 — 3 y = 1 + y -1/3 = y — 1/3 -1/3
3 z — 5 2 = z — 5/3 2/3
Получено уравнение второй прямой в канонической форме
x — 2 -2 = y — 1/3 -1/3 = z — 5/3 2/3
— направляющий вектор второй прямой.
cos φ = 3·(-2) + 4·(- 1 3 ) + 5· 2 3 3 2 + 4 2 + 5 2 · (-2) 2 + (- 1 3 ) 2 + ( 2 3 ) 2 = -6 — 4 3 + 10 3 9 + 16 + 25 · 4 + 1 9 + 4 9 = -4 50 · 41/9 = 12 5 82 = 6 82 205
Видео:Угол между прямыми в пространстве. 11 класс.Скачать
Угол между прямыми онлайн
С помощью этого онлайн калькулятора можно найти угол между прямыми. Дается подробное решение с пояснениями. Для вычисления угла между прямыми, задайте размерность (2-если рассматривается прямая на плоскости, 3- если рассматривается прямая в пространстве), выберите вид уравнения (канонический, параметрический, общий (для двухмерного пространства)), введите данные в ячейки и нажмите на кнопку «Решить». Теоретическую часть и численные примеры смотрите ниже.
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Видео:Найти угол между плоскостямиСкачать
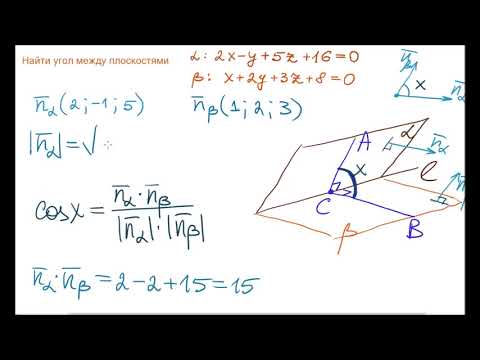
1. Угол между прямыми на плоскости
Прямые заданы каноническими уравнениями
1.1. Определение угла между прямыми
Пусть в двухмерном пространстве прямые L1 и L2 заданы каноническими уравнениями
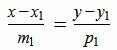 , , | (1.1) |
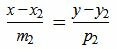 , , | (1.2) |
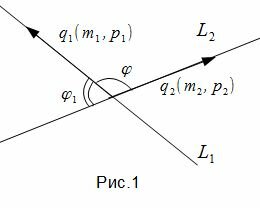
Задача об определении угла между прямыми L1 и L2 сводится к задаче об определении угла между направляющими векторами q1 и q2 (рис.1).
 , , |
 , , | (1.3) |
Из выражения (1.3) получим:
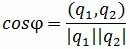 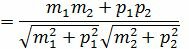 . . | (1.4) |
Таким образом, из формулы (1.4) можно найти угол между прямыми L1 и L2. Как видно из Рис.1 пересекающиеся прямые образуют смежные углы φ и φ1. Если найденный угол больше 90°, то можно найти минимальный угол между прямыми L1 и L2: φ1=180-φ.
Из формулы (1.4) можно вывести условия параллельности и перпендикулярности двух прямых.
Пример 1. Определить угол между прямыми
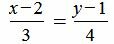 . . | (1.5) |
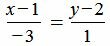 . . | (1.6) |
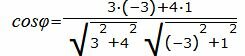 . . |
Упростим и решим:
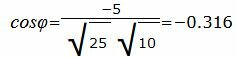 . . |
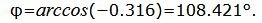 |
Данный угол больше 90°. Найдем минимальный угол между прямыми. Для этого вычтем этот угол из 180:
 |
Угол между прямыми равен:
 |
1.2. Условие параллельности прямых
Пусть φ=0. Тогда cosφ=1. При этом выражение (1.4) примет следующий вид:
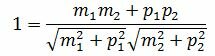 . . | (1.7) |
Сделаем преобразования с выражением (1.7):
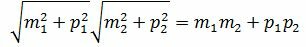 , , |
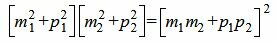 , , |
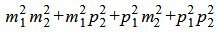 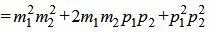 , , |
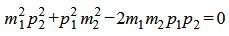 , , |
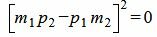 , , |
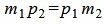 . . | (1.8) |
Таким образом условие параллельности прямых L1 и L2 имеет вид (1.8). Если m2≠0 и p2≠0, то (1.8) можно записать так:
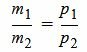 . . | (1.9) |
Пример 2. Определить, параллельны ли прямые
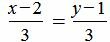 . . | (1.10) |
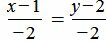 . . | (1.11) |
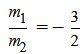 , , 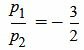 . . |
Удовлетворяется равенство (1.9), следовательно прямые (1.10) и (1.11) параллельны.
Ответ. Прямые (1.10) и (1.11) параллельны.
1.3. Условие перпендикулярности прямых
Пусть φ=90°. Тогда cosφ=0. При этом выражение (1.4) примет следующий вид:
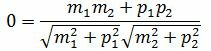 . . | (1.12) |
Правая часть выражения (1.12) равно нулю тогда и только тогда, когда числитель равен нулю. Следовательно, для того, чтобы прямые L1 и L2 были перпендикулярны , должно выполняться условие
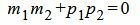 . . | (1.13) |
Пример 3. Определить, перпендикулярны ли прямые
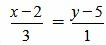 | (1.14) |
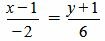 . . | (1.15) |
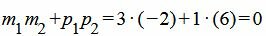 . . | (16) |
Удовлетворяется условие (1.13), следовательно прямые (1.14) и (1.15) перпендикулярны.
Ответ. Прямые (1.14) и (1.15) перпендикулярны.
Прямые заданы общими уравнениями
1.4. Определение угла между прямыми
Пусть две прямые L1 и L2 заданы общими уравнениями
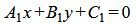 | (1.17) |
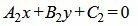 . . | (1.18) |
Так как нормальным вектором прямой L1 является n1=(A1, B1), а нормальным вектором прямой L2 является n2=(A2, B2), то задача об определении угла между прямыми L1 и L2 сводится к определению угла φ между векторами n1 и n2 (Рис.2).
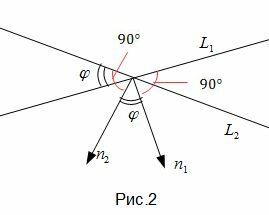 . . |
Из определения скалярного произведения двух векторов, имеем:
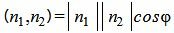 . . | (1.19) |
Из уравнения (19) получим
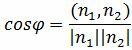 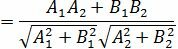 . . | (1.20) |
Пример 4. Найти угол между прямыми
| 5x1−2x2+3=0 | (1.21) |
| x1+3x2−1=0. | (1.22) |
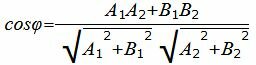 | (23) |
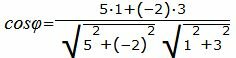 |
Упростим и решим:
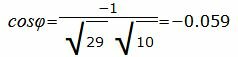 |
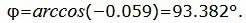 |
Данный угол больше 90°. Найдем минимальный угол между прямыми. Для этого вычтем этот угол из 180:
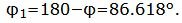 |
1.5. Условие параллельности прямых
Так как угол между паралленьными прямыми равен нулю, то φ=0, cos(φ)=1. Тогда сделав преобразования, представленные выше для канонических уравнений прямых получим условие параллельности:
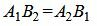 . . | (1.24) |
С другой стороны условие параллельности прямых L1 и L2 эквивалентно условию коллинеарности векторов n1 и n2 и можно представить так:
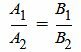 . . | (1.25) |
Как видим уравнения (1.24) и (1.25) эквивалентны при A2≠0 и B2≠0. Если в координатах нормальных векторов существует нулевой коэффициент, то нужно использовать уравнение (1.24).
Пример 5. Определить, параллельны ли прямые
| 4x+2y+2=0 | (1.26) |
Удовлетворяется равенство (1.24), следовательно прямые (1.26) и (1.27) параллельны.
Ответ. Прямые (1.26) и (1.27) параллельны.
1.6. Условие перпендикулярности прямых
Условие перпендикулярности прямых L1 и L2 можно извлекать из формулы (1.20), подставляя cos(φ)=0. Тогда скалярное произведение (n1,n2)=0. Откуда
| A1A2+B1B2=0. | (1.28) |
Таким образом условие перпендикулярности прямых определяется равенством (1.28).
Пример 6. Определить, перпендикулярны ли прямые
| 4x−1y+2=0 | (1.29) |
| 2x+8y−14=0. | (1.30) |
Удовлетворяется равенство (1.28), следовательно прямые (1.29) и (1.30) перпендикулярны.
Ответ. Прямые (1.29) и (1.30) перпендикулярны.
Видео:Угол между кривымиСкачать

2. Угол между прямыми в пространстве
2.1. Определение угла между прямыми
Пусть в пространстве прямые L1 и L2 заданы каноническими уравнениями
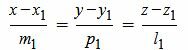 , , | (2.1) |
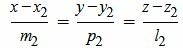 , , | (2.2) |
Задача об определении угла между прямыми L1 и L2 сводится к задаче об определении угла между направляющими векторами q1 и q2 .
 , , | (2.3) |
Из выражения (2.3) получим:
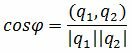 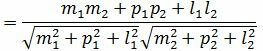 . . | (2.4) |
Таким образом, из формулы (2.4) можно найти угол между прямыми L1 и L2. Если найденный угол больше 90°, то можно найти минимальный угол между прямыми L1 и L2: φ1=180-φ.
Из формулы (2.4) можно вывести условия параллельности и перпендикулярности двух прямых.
Пример 1. Определить угол между прямыми
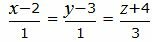 . . | (2.5) |
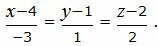 | (2.6) |
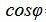 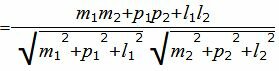 . . |
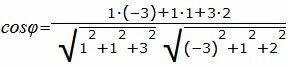 . . |
Упростим и решим:
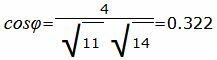 . . |
 |
Угол между прямыми равен:
 |
2.2. Условие параллельности прямых
Условие параллельности прямых эквивалентно условию коллинеарности направляющих векторов q1 и q2, т.е. соответствующие координаты этих векторов пропорциональны. Пусть
| m1=αm2, p1=αp2, l1=αl2 | (2.7) |
где α − некоторое число. Тогда соответствующие координаты векторов q1 и q2 пропорциональны, и, следовательно прямые L1 и L2 параллельны.
Условие параллельности прямых можно представить и так:
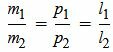 | (2.8) |
Отметим, что любую пропорцию 
Пример 2. Определить, параллельны ли прямые
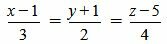 . . | (2.9) |
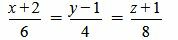 . . | (2.10) |
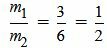 , , 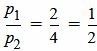 , , 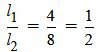 . . |
Удовлетворяется равенство (2.8) (или (2.7)), следовательно прямые (2.9) и (2.10) параллельны.
Ответ. Прямые (2,9) и (2,10) параллельны.
Пример 3. Определить, параллельны ли прямые
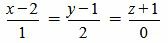 . . | (2.11) |
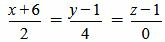 . . | (2.12) |
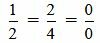 . . | (2.13) |
Выражение (2.13) нужно понимать так:
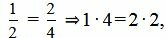 , , 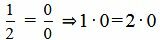 , , 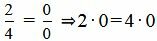 . . | (2.14) |
Как мы видим из (2.14) условия (2.13) выполняются. Следовательно прямые (2.11) и (2.12) параллельны.
Ответ. Прямые (2.11) и (2.12) параллельны.
2.3. Условие перпендикулярности прямых
Пусть φ=90°. Тогда cosφ=0. При этом выражение (2.4) примет следующий вид:
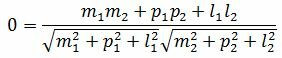 . . | (2.15) |
Правая часть выражения (2.15) равно нулю тогда и только тогда, когда числитель равен нулю. Следовательно, для того, чтобы прямые L1 и L2 были перпендикулярны , должно выполняться условие
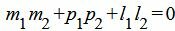 . . | (2.16) |
Пример 3. Определить, перпендикулярны ли прямые
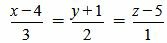 | (2.17) |
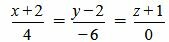 . . | (2.18) |
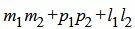 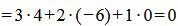 . . | (2.19) |
Удовлетворяется условие (2.16), следовательно прямые (2.17) и (2.18) перпендикулярны.
Ответ. Прямые (2.17) и (2.18) перпендикулярны.
Видео:Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать

VMath
Инструменты сайта
Основное
Навигация
Информация
Действия
Содержание
Видео:§16 Угол между двумя прямыми на плоскостиСкачать
Длина дуги, угол между линиями, площадь области на поверхности
Видео:Видеоурок "Уравнение прямой с угловым коэффициентом"Скачать

Краткие теоретические сведения
Зная первую квадратичную форму поверхности, мы можем решить три задачи:
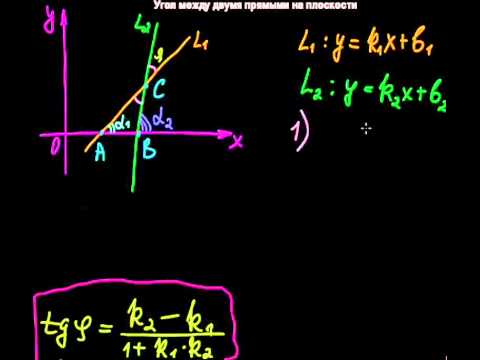
2. Найти угол между двумя линиями на поверхности в точке их пересечения:
Если две линии, лежащие на поверхности с первой квадратичной формой $I_1=E,du^2+2F,du,dv+G,dv^2$, пересекаются в некоторой точке $P$ поверхности и имеют в этой точке направления $(du:dv)$ и $(delta u:delta v)$, то косинус угла между ними определяется по формуле: begin mbox,varphi = displaystylefrac<sqrtcdotsqrt> \ mbox,varphi = displaystylefrac<sqrtcdotsqrt>. end Говорим, что кривая на поверхности $vec=vec(u,v)$ в точке $(u,v)$ имеет направление $(du:dv)$, если вектор $dvec=vec_udu+vec_vdv$ является касательным вектором кривой в этой точке.
3. Найти площадь области $Omega$ на поверхности: begin S = iintlimits_sqrtdu,dv, end где $D$ — прообраз $Omega$ на плоскости $(u,v)$.
Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Решение задач
Задача 1 (почти Феденко 684)
Найти длину дуги кривой, заданной уравнениями $v=3u$ на поверхности с первой квадратичной формой begin I_1=du^2+frac19,mbox^2u,dv^2 end между точками $M_1(u_1,v_1)$ и $M_2(u_2,v_2)$.
Решение задачи 1
Задача 2 (почти Феденко 682)
Под каким углом пересекаются линии $$ u+v=a, ,, u-v=a,$$ лежащие на поверхности: begin x=u,mboxv, ,, y=u,mbox,v, ,, z=au. end
Решение задачи 2
Первая квадратичная форма данной поверхности: begin I_1=(1+a^2),du^2+u^2,dv^2. end
Данные линии пересекаются в точке: begin left < beginu+v&=a,\ u-v&=a. end right. quad Rightarrow quad P(u=a,v=0). end
Направления данных линий: begin du+dv=0, ,, delta u-delta v=0,, Rightarrow end begin du = -dv, ,, delta u = delta v. end
Задача 3
Дана поверхность: $$z=axy.$$ Найти углы между координатными линиями.
Решение задачи 3
Координатные линии на данной поверхности задаются уравнениями: $x=x_0$, $y=y_0$. Запишем коэффициенты первой квадратичной формы: begin &E=1+(z_x)^2=1+a^2y^2,\ &F=z_xz_y=a^2xy, \ &G=1+(z_y)^2=1+a^2x^2. end
Направления координатных линий: begin &x=x_0 ,, Rightarrow dx=0,\ &y=y_0 ,, Rightarrow delta y=0. end
Задача 4 (Дополнение к Задаче 3)
Как мы вывели в примере выше, угол между координатными линиями равен
Из формулы следует, что координатная сеть поверхности ортогональна (координатные линии пересекаются под прямым углом), тогда и только тогда, когда $F$=0.
Задача 5 (Феденко 683)
Найти периметр и внутренние углы криволинейного треугольника $$ u=pm av^2/2,,, v=1,$$ расположенного на поверхности $$I_1=du^2+(u^2+a^2)dv^2.$$

Зная координаты вершин и уравнения сторон, найдем длины дуг, составляющих стороны треугольника $ABC$, и углы между линиями в точках их пересечения, то есть в вершинах треугольника: begin &s_1 = |BC| = a,\ &s_2 = |AC| = frac76 a,\ &s_3 = |BC| = frac76 a,\ &P_=s_1+s_2+s_3=fraca. end begin &mbox,A = 1, ,, mbox,B=mbox,C=frac23. end
📺 Видео
21. Угол между прямой и плоскостьюСкачать

Угол между прямыми в пространстве. Практическая часть. 10 класс.Скачать

Математика без Ху!ни. Взаимное расположение прямой и плоскости.Скачать

Угол между прямой и плоскостью. Видеоурок по геометрии 10 классСкачать

10 класс, 21 урок, Угол между прямой и плоскостьюСкачать

10 класс, 43 урок, Уравнение касательной к графику функцииСкачать

Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Угол между прямыми в пространстве. Практическая часть. 11 класс.Скачать

Лекция 23. Виды уравнений прямой на плоскости.Скачать







