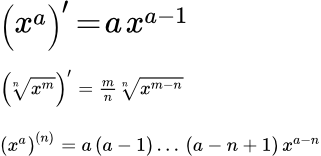Как найти производную от числа со степенью квадратного уравнения

Как найти производную степенной функции: формула, примеры

Таблица производных и правила дифференцирования

Основные ссылки – таблица производных , правила дифференцирования и примеры решений (10 шт) .

Задание. Найти производную функции

Решение. Так как производная суммы равна сумме производных, то

Воспользуемся формулами для производных показательной и обратной тригонометрической функций:

Ответ.

Производные сложных функций

Основные ссылки – теоретический материал и примеры решений (10 шт) .

Задание.Найти производную функции

Решение. По правилу дифференцирования сложной функции:

В свою очередь производная также берется по правилу дифференцирования сложной функции:

Ответ.

Производные элементарных функций

Элементарные функции — это все, что перечислено ниже. Производные этих функций надо знать наизусть. Тем более что заучить их совсем несложно — на то они и элементарные.

Итак, производные элементарных функций:

Название	Функция	Производная
Константа	f ( x ) = C , C ∈ R	0 (да-да, ноль!)
Степень с рациональным показателем	f ( x ) = x n	n · x n − 1
Синус	f ( x ) = sin x	cos x
Косинус	f ( x ) = cos x	− sin x (минус синус)
Тангенс	f ( x ) = tg x	1/cos 2 x
Котангенс	f ( x ) = ctg x	− 1/sin 2 x
Натуральный логарифм	f ( x ) = ln x	1/ x
Произвольный логарифм	f ( x ) = log a x	1/( x · ln a )
Показательная функция	f ( x ) = e x	e x (ничего не изменилось)

Если элементарную функцию умножить на произвольную постоянную, то производная новой функции тоже легко считается:

В общем, константы можно выносить за знак производной. Например:

(2 x 3 )’ = 2 · ( x 3 )’ = 2 · 3 x 2 = 6 x 2 .

Очевидно, элементарные функции можно складывать друг с другом, умножать, делить — и многое другое. Так появятся новые функции, уже не особо элементарные, но тоже дифференцируемые по определенным правилам.

Геометрический и физический смысл производной

Пусть есть функция f(x), заданная в некотором интервале (a, b). Точки х и х0 принадлежат этому интервалу. При изменении х меняется и сама функция. Изменение аргумента – разность его значений х-х0. Эта разность записывается как дельта икс и называется приращением аргумента. Изменением или приращением функции называется разность значений функции в двух точках. Определение производной:

Производная функции в точке – предел отношения приращения функции в данной точке к приращению аргумента, когда последнее стремится к нулю.

Иначе это можно записать так:

Какой смысл в нахождении такого предела? А вот какой:

Геометрический смысл производной: производная от функции в точке равна тангенсу угла между осью OX и касательной к графику функции в данной точке.

Физический смысл производной: производная пути по времени равна скорости прямолинейного движения.

Действительно, еще со школьных времен всем известно, что скорость – это частное пути x=f(t) и времени t. Средняя скорость за некоторый промежуток времени:

Чтобы узнать скорость движения в момент времени t0 нужно вычислить предел:

Приведем пример, иллюстрирующий практическое применение производной. Пусть тело движется то закону:

Нам нужно найти скорость в момент времени t=2c. Вычислим производную:

Производная функции с экспонентой

Тут на самом деле 2 функции: экспонента и степенная функция (с отрицательным показателем -1). Отсюда и поэтапное вычисление этой производной. В заблуждение может ввести натуральный логарифм, но заметьте – натуральный логарифм от 5 все лишь число.

Понятие производной сложной функции

Если g(x) и f(u) – дифференцируемые функции своих аргументов соответственно в точках x и u = g(x), то сложная функция также дифференцируема в точке x и находится по формуле

Типичная ошибка при решении задач на производные – машинальное перенесение правил дифференцирования простых функций на сложные функции. Будем учиться избегать этой ошибки.

Посмотрите на формулу 9 в таблице производных . Исходная функция является функцией от функции, причём аргумент x является аргументом лишь второй функции, а вторая функция является аргументом первой функции, или, согласно более строгому определению – промежуточным аргументом по независимой переменной x.

А теперь посмотрите на картинку ниже, которая иллюстрирует решение задач на сложные производные по аналогии с простым примером из кулинарии – приготовлении запечёных яблок, фаршированных ягодами.

Итак, “яблоко” – это функция, аргументом которой является промежуточный аргумент, а промежуточный аргумент по независимой переменной x, в свою очередь, является “фаршем” (ягодами). Представим себе, что решая задачи на производные сложной функции, сначала помещаем яблоко с фаршем в особую (физико-математическую) духовку и устанавливаем режим 1. При таком режиме духовка воздействует только на “яблоко”, поскольку нужно, допустим, больше пропечь яблоко, а фарш из ягод оставить более сочным, то есть обрабатывать в другом режиме. Итак, в при режиме 1 обрабатывается яблоко, а фарш остаётся незатронутым, или, ближе к нашим задачам, находим производную функции лишь от промежуточного аргумента, то есть, “яблока”. Затем в духовке устанавливается режим 2, который воздействует только на фарш, иначе говоря, записываем производную функции, являющейся промежуточным аргументом по независимой переменной x. И, в конце концов, записываем произведение производной “яблока” и производной “фарша”. Можно подавать!

Пример 1.Найти производную функции

Сначала определим, где здесь “яблоко”, то есть функция по промежуточному аргументу u, а где “фарш”, то есть промежуточный аргумент u по независимой переменной x. Определяем: возведение в степень – это функция по промежуточному аргументу, то есть “яблоко”, а выражение в скобках (разность двух тригонометрических функций) – это промежуточный аргумент, то есть “фарш”.

Далее по таблице производных (производная суммы или разности, производные синуса и косинуса) находим:

Требуемая в условии задачи производная (готовое “фаршированое яблоко”):

Нахождение производной сложной логарифмической функции имеет свои особенности, поэтому у нас есть и урок “Производная логарифмической функции”.

Пример 2.Найти производную функции

Неправильное решение: вычислять натуральный логарифм каждого слагаемого в скобках и искать сумму производных:

Правильное решение: опять определяем, где “яблоко”, а где “фарш”. Здесь натуральный логарифм от выражения в скобках – это “яблоко”, то есть функция по промежуточному аргументу u, а выражение в скобках – “фарш”, то есть промежуточный аргумент u по независимой переменной x.

Тогда (применяя формулу 14 из таблицы производных)

Во многих реальных задачах выражение с логарифмом бывает несколько сложнее, поэтому и есть урок “Производная логарифмической функции”.

Пример 3.Найти производную функции

Правильное решение. В очередной раз определяем, где “яблоко”, а где “фарш”. Здесь косинус от выражения в скобках (формула 7 в таблице производных)- это “яблоко”, оно готовится в режиме 1, воздействующем только на него, а выражение в скобках (производная степени – номер 3 в таблице производных) – это “фарш”, он готовится при режиме 2, воздействующей только на него. И как всегда соединяем две производные знаком произведения. Результат:

Производная сложной логарифмической функции – частое задание на контрольных работах, поэтому настоятельно рекомендуем посетить урок “Производная логарифмической функции”.

Первые примеры были на сложные функции, в которых промежуточный аргумент по независимой переменной был простой функцией. Но в практических заданиях нередко требуется найти производную сложной функции, где промежуточный аргумент или сам является сложной функцией или содержит такую функцию. Что делать в таких случаях? Находить производные таких функций по таблицам и правилам дифференцирования . Когда найдена производная промежуточного аргумента, она просто подставляется в нужное место формулы. Ниже – два примера, как это делается.

Кроме того, полезно знать следующее. Если сложная функция может быть представлена в виде цепочки из трёх функций

,

то её производную следует находить как произведение производных каждой из этих функций:

.

Для решения многих ваших домашних заданий может потребоваться открыть в новых окнах пособия Действия со степенями и корнями и Действия с дробями .

Пример 4.Найти производную функции

Применяем правило дифференцирования сложной функции, не забывая, что в полученном произведении производных промежуточный аргумент по независимой переменной x не меняется:

Готовим второй сомножитель произведения и применяем правило дифференцирования суммы:

Второе слагаемое – корень, поэтому

Таким образом получили, что промежуточный аргумент, являющийся суммой, в качестве одного из слагаемых содержит сложную функцию: возведение в степень – сложная функция, а то, что возводится в степень – промежуточный аргумент по независимой переменной x.

Поэтому вновь применим правило дифференцирования сложной функции:

Степень первого сомножителя преобразуем в корень, а дифференцируя второй сомножитель, не забываем, что производная константы равна нулю:

Теперь можем найти производную промежуточного аргумента, нужного для вычисления требуемой в условии задачи производной сложной функции y:

Пример 5.Найти производную функции

Сначала воспользуемся правилом дифференцирования суммы:

Получили сумму производных двух сложных функций. Находим первую из них:

Здесь возведение синуса в степень – сложная функция, а сам синус – промежуточный аргумент по независимой переменной x. Поэтому воспользуемся правилом дифференцирования сложной функции, попутно вынося множитель за скобки :

Теперь находим второе слагаемое из образующих производную функции y:

Здесь возведение косинуса в степень – сложная функция f[g(x)], а сам косинус – промежуточный аргумент по независимой переменной x. Снова воспользуемся правилом дифференцирования сложной функции:

Результат – требуемая производная:

Определение и формулы

Заметим, что степенно-показательную функцию можно представить в показательном виде:
.
Поэтому ее также называют сложной показательной функцией.

Далее мы покажем, что производная степенно-показательной функции определяется по формуле:
(1) .

Пошаговые примеры – как найти производную

Пример 3. Найти производную функции

.

Решение. Определяем части выражения функции: всё выражение представляет произведение, а его сомножители – суммы, во второй из которых одно из слагаемых содержит постоянный множитель. Применяем правило дифференцирования произведения: производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой:

Далее применяем правило дифференцирования суммы: производная алгебраической суммы функций равна алгебраической сумме производных этих функций. В нашем случае в каждой сумме второе слагаемое со знаком минус. В каждой сумме видим и независимую переменную, производная которой равна единице, и константу (число), производная которой равна нулю. Итак, “икс” у нас превращается в единицу, а минус 5 – в ноль. Во втором выражении “икс” умножен на 2, так что двойку умножаем на ту же единицу как производную “икса”. Получаем следующие значения производных:

Подставляем найденные производные в сумму произведений и получаем требуемую условием задачи производную всей функции:

А проверить решение задачи на производную можно на калькуляторе производных онлайн .

Пример 4. Найти производную функции

Решение. От нас требуется найти производную частного. Применяем формулу дифференцирования частного: производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя. Получаем:

Производную сомножителей в числителе мы уже нашли в примере 2. Не забудем также, что произведение, являющееся вторым сомножителем в числителе в текущем примере берётся со знаком минус:

Если Вы ищете решения таких задач, в которых надо найти производную функции, где сплошное нагромождение корней и степеней, как, например, , то добро пожаловать на занятие “Производная суммы дробей со степенями и корнями” .

Если же Вам нужно узнать больше о производных синусов, косинусов, тангенсов и других тригонометрических функций, то есть, когда функция имеет вид вроде , то Вам на урок “Производные простых тригонометрических функций” .

Пример 5. Найти производную функции

Решение. В данной функции видим произведение, один из сомножителей которых – квадратный корень из независимой переменной, с производной которого мы ознакомились в таблице производных. По правилу дифференцирования произведения и табличному значению производной квадратного корня получаем:

Проверить решение задачи на производную можно на калькуляторе производных онлайн .

Пример 6. Найти производную функции

Решение. В данной функции видим частное, делимое которого – квадратный корень из независимой переменной. По правилу дифференцирования частного, которое мы повторили и применили в примере 4, и табличному значению производной квадратного корня получаем:

Чтобы избавиться от дроби в числителе, умножаем числитель и знаменатель на :

Проверить решение задачи на производную можно на калькуляторе производных онлайн .

Примеры решения задач

Задание

Найти производную функции

РешениеИскомая производная

Производная от суммы или разности функция равна сумме или разности их производных, то есть

Производную от найдем как производную от степенной функции:

Для нахождения производной одночлена вначале константу вынесем за знак производной:

Далее дробь представим как степень с отрицательным показателем по свойству представим как степень с отрицательным показателем по свойству :

Далее производную находим как от степенной функции:

Для нахождения производной запишем корень в виде степени с дробным показателем:

Далее производную находим как от степенной функции:

Записываем дробную степень в виде корня:

Производная от двойки, как от константы, равна нулю:

Итак, окончательно имеем:

Ответ

Задание	Найти производную функции
Решение	Искомая производная

Данную производную находим как производную от степенной функции, но так как основание степени является сложной функцией (отличается от просто является сложной функцией (отличается от просто ), то нужно еще умножить на производную от основания:

Найдем отдельно оставшуюся производную. Производная о суммы равна сумме производных:

Из первого слагаемого вынесем константу за знак производной, а производная от второго, как от константы, равна нулю:

Производная от равна единице:

Таким образом, производная заданной функции

Ответ

Применение дифференциала в приближенных вычислениях

Основные ссылки – теоретический материал и примеры решений (10 шт) .

Задание. Вычислить приближенно , заменяя приращение функции ее дифференциалом.

Решение. Рассмотрим функцию . Необходимо вычислить ее значение в точке . Представим данное значение в виде следующей суммы:

Величины и выбираются так, чтобы в точке можно было бы достаточно легко вычислить значение функции и ее производной, а было бы достаточно малой величиной. С учетом этого, делаем вывод, что , то есть , .

Вычислим значение функции в точке :

Далее продифференцируем рассматриваемую функцию и найдем значение :

Ответ.

Производная суммы и разности

Пусть даны функции f ( x ) и g ( x ), производные которых нам известны. К примеру, можно взять элементарные функции, которые рассмотрены выше. Тогда можно найти производную суммы и разности этих функций:

Итак, производная суммы (разности) двух функций равна сумме (разности) производных. Слагаемых может быть больше. Например, ( f + g + h )’ = f ’ + g ’ + h ’.

Строго говоря, в алгебре не существует понятия «вычитание». Есть понятие «отрицательный элемент». Поэтому разность f − g можно переписать как сумму f + (−1) · g , и тогда останется лишь одна формула — производная суммы.

Задача. Найти производные функций: f ( x ) = x 2 + sin x; g ( x ) = x 4 + 2 x 2 − 3.

Функция f ( x ) — это сумма двух элементарных функций, поэтому:

f ’( x ) = ( x 2 + sin x )’ = ( x 2 )’ + (sin x )’ = 2 x + cos x;

Аналогично рассуждаем для функции g ( x ). Только там уже три слагаемых (с точки зрения алгебры):

g ’( x ) = ( x 4 + 2 x 2 − 3)’ = ( x 4 + 2 x 2 + (−3))’ = ( x 4 )’ + (2 x 2 )’ + (−3)’ = 4 x 3 + 4 x + 0 = 4 x · ( x 2 + 1).

Ответ:
f ’( x ) = 2 x + cos x;
g ’( x ) = 4 x · ( x 2 + 1).

Таблица производных часто встречающихся функций

В следующей таблице приведены формулы для производных от степенных, показательных (экспоненциальных), логарифмических, тригонометрических и обратных тригонометрических функций. Доказательство большинства их этих формул выходит за рамки школьного курса математики.

где c – любое число

где c – любое число

где a – любое положительное число, не равное 1

где a – любое положительное число, не равное 1

y = tg x ,

y = ctg x ,

y = arcsin x ,

y = arccos x ,

Функция	Формула для производной	Название формулы
y’ = 0	Производная от постоянной функции
y’ = c x c – 1	Производная степенной функции
y = e x	y’ = e x	Производная от экспоненты (показательной функции с основанием e )
y’ = a x ln a	Производная от показательной функции с основанием a
y = ln x , x > 0	, x > 0	Производная от натурального логарифма
, x > 0	Производная от логарифма по основанию a
y = sin x	y’ = cos x	Производная синуса
y = cos x	y’ = – sin x	Производная косинуса
, ,	Производная тангенса
, ,	Производная котангенса
	Производная арксинуса
	Производная арккосинуса
y = arctg x		Производная арктангенса
y = arcctg x		Производная арккотангенса

где c – любое число

Формула для производной:

где c – любое число

Формула для производной:

Формула для производной:

где a – любое положительное число, не равное 1

Формула для производной:

Формула для производной:

, x > 0

где a – любое положительное число, не равное 1

Формула для производной:

, x > 0

Формула для производной:

Формула для производной:

Формула для производной:

,

y = arccos x ,

Формула для производной:

Формула для производной:

Формула для производной:

Производная от постоянной функции

Производная степенной функции

Производная от экспоненты (показательной функции с основанием e )

Производная от показательной функции с основанием a

Производная от натурального логарифма

Производная от логарифма по основанию a

Производная синуса

Производная косинуса

Производная тангенса

Производная котангенса

Формула для производной:

Производная арксинуса

y = arcsin x , Формула для производной:

Производная арккосинуса

Производная арктангенса

Производная арккотангенса

Найти производные самостоятельно, а затем посмотреть решения

Пример 7. Найти производную функции

.

Правильное решение и ответ .

Пример 8. Найти производную функции

.

Правильное решение и ответ .

Пример 9. Найти производную функции

, где a и b – константы.

Правильное решение и ответ .

Пример 10. Найти производную функции

.

Правильное решение и ответ .

Пример 11. Найти производную функции

.

Правильное решение и ответ .

Производная функции с корнем

Степенная функция плюс осложнение внутри скобки. Пример не дорешан, всего лишь нужно вспомнить из таблицы пару элементарных функций.

Логарифмическая производная

Если производная от логарифмов – это такая сладкая музыка, то возникает вопрос, а нельзя ли в некоторых случаях организовать логарифм искусственно? Можно! И даже нужно.

Найти производную функции

Похожие примеры мы недавно рассмотрели. Что делать? Можно последовательно применить правило дифференцирования частного, а потом правило дифференцирования произведения. Недостаток способа состоит в том, что получится огромная трехэтажная дробь, с которой совсем не хочется иметь дела.

Но в теории и практике есть такая замечательная вещь, как логарифмическая производная. Логарифмы можно организовать искусственно, «навесив» их на обе части:

Примечание: т.к. функция может принимать отрицательные значения, то, вообще говоря, нужно использовать модули: , которые исчезнут в результате дифференцирования. Однако допустимо и текущее оформление, где по умолчанию принимаются во внимание комплексные значения. Но если со всей строгостью, то и в том и в другом случае следует сделать оговорку, что , которые исчезнут в результате дифференцирования. Однако допустимо и текущее оформление, где по умолчанию принимаются во внимание комплексные значения. Но если со всей строгостью, то и в том и в другом случае следует сделать оговорку, что .

Теперь нужно максимально «развалить» логарифм правой части (формулы перед глазами?). Я распишу этот процесс очень подробно:

Собственно приступаем к дифференцированию.
Заключаем под штрих обе части:

Производная правой части достаточно простая, её я комментировать не буду, поскольку если вы читаете этот текст, то должны уверенно с ней справиться.

Как быть с левой частью?

В левой части у нас сложная функция. Предвижу вопрос: «Почему, там же одна буковка «игрек» под логарифмом?».

Дело в том, что эта «одна буковка игрек» – САМА ПО СЕБЕ ЯВЛЯЕТСЯ ФУНКЦИЕЙ (если не очень понятно, обратитесь к статье Производная от функции, заданной неявно ). Поэтому логарифм – это внешняя функция, а «игрек» – внутренняя функция. И мы используем правило дифференцирования сложной функции :

В левой части как по мановению волшебной палочки у нас «нарисовалась» производная . Далее по правилу пропорции перекидываем «игрек» из знаменателя левой части наверх правой части:

А теперь вспоминаем, о каком таком «игреке»-функции мы рассуждали при дифференцировании? Смотрим на условие:

Окончательный ответ:

Найти производную функции

Это пример для самостоятельного решения. Образец оформления примера данного типа в конце урока.

С помощью логарифмической производной можно было решить любой из примеров № 4-7, другое дело, что там функции проще, и, может быть, использование логарифмической производной не слишком-то и оправдано.

Производная сложной степенной функции

В сложной функции вместо x представлено более сложное выражение. Производная такой функции определяется по формуле:

Правила нахождения производных

Сам процесс нахождения производной называется дифференцированием. Функция, которая имеет производную в данной точке, называется дифференцируемой.

Как найти производную? Согласно определению, нужно составить отношение приращения функции и аргумента, а затем вычислить предел при стремящемся к нулю приращении аргумента. Конечно, можно вычислять все производные так, но на практике это слишком долгий путь. Все уже давно посчитано до нас. Ниже приведем таблицу с производными элементарных функций, а затем рассмотрим правила вычисления производных, в том числе и производных сложных функций с подробными примерами.

Таблица производных некоторых сложных функций

Для сложных функций на основании правила дифференцирования сложной функции формула производной простой функции принимает другой вид.

1. Производная сложной степенной функции, где u – дифференцируемая функция аргумента x
2. Производная корня от выражения
3. Производная показательной функции
4. Частный случай показательной функции
5. Производная логарифмической функции с произвольным положительным основанием а
6. Производная сложной логарифмической функции, где u – дифференцируемая функция аргумента x
7. Производная синуса
8. Производная косинуса
9. Производная тангенса
10. Производная котангенса
11. Производная арксинуса
12. Производная арккосинуса
13. Производная арктангенса
14. Производная арккотангенса

Примеры

Решим примеры. Преобразования, позволяющие применить другие свойства производной, мы применять не будем. В решениях будем использовать только формулу производной от дроби.

По условию даются функции. Нужно найти производные.

Рисунок 2. Пример. Автор24 — интернет-биржа студенческих работ

Рисунок 3. Пример. Автор24 — интернет-биржа студенческих работ

Рисунок 4. Пример. Автор24 — интернет-биржа студенческих работ

Производная произведения

Математика — наука логичная, поэтому многие считают, что если производная суммы равна сумме производных, то производная произведения strike “>равна произведению производных. А вот фиг вам! Производная произведения считается совсем по другой формуле. А именно:

( f · g ) ’ = f ’ · g + f · g ’

Формула несложная, но ее часто забывают. И не только школьники, но и студенты. Результат — неправильно решенные задачи.

Задача. Найти производные функций: f ( x ) = x 3 · cos x; g ( x ) = ( x 2 + 7 x − 7) · e x .

Функция f ( x ) представляет собой произведение двух элементарных функций, поэтому все просто:

f ’( x ) = ( x 3 · cos x )’ = ( x 3 )’ · cos x + x 3 · (cos x )’ = 3 x 2 · cos x + x 3 · (− sin x ) = x 2 · (3cos x − x · sin x )

У функции g ( x ) первый множитель чуть посложней, но общая схема от этого не меняется. Очевидно, первый множитель функции g ( x ) представляет собой многочлен, и его производная — это производная суммы. Имеем:

g ’( x ) = (( x 2 + 7 x − 7) · e x )’ = ( x 2 + 7 x − 7)’ · e x + ( x 2 + 7 x − 7) · ( e x )’ = (2 x + 7) · e x + ( x 2 + 7 x − 7) · e x = e x · (2 x + 7 + x 2 + 7 x −7) = ( x 2 + 9 x ) · e x = x ( x + 9) · e x .

Ответ:
f ’( x ) = x 2 · (3cos x − x · sin x );
g ’( x ) = x ( x + 9) · e x .

Обратите внимание, что на последнем шаге производная раскладывается на множители. Формально этого делать не нужно, однако большинство производных вычисляются не сами по себе, а чтобы исследовать функцию. А значит, дальше производная будет приравниваться к нулю, будут выясняться ее знаки и так далее. Для такого дела лучше иметь выражение, разложенное на множители.

Продолжаем искать производные вместе

Пример 12. Найти производную функции

.

Решение. Применяя правила вычисления производной алгебраической суммы функций, вынесения постоянного множителя за знак производной и формулу производной степени (в таблице производных – под номером 3), получим

.

Пример 13. Найти производную функции

Решение. Применим правило дифференцирования произведения, а затем найдём производные сомножителей, так же, как в предыдущей задаче, пользуясь формулой 3 из таблицы производных. Тогда получим

Пример 14. Найти производную функции

Решение. Как и в примерах 4 и 6, применим правило дифференцирования частного:

Теперь вычислим производные в числителе и перед нами уже требуемый результат:

Пример 15.Найти производную функции

Шаг1. Применяем правило дифференцирования суммы:

Шаг2. Найдём производную первого слагаемого. Это табличная производная квадратного корня (в таблице производных – номер 5):

Шаг3. В частном знаменатель – также корень, только не квадратный. Поэтому преобразуем этот корень в степень:

и далее дифференцируем частное, не забывая, что число 2 в первом слагаемом числителя – это константа, производная которой равна нулю, и, следовательно всё первое слагаемое равно нулю:

Корень из константы, как не трудно догадаться, является также константой, а производная константы, как мы знаем из таблицы производных, равна нулю:

,

а производная, требуемая в условии задачи:

Синтаксис описания формул

В описании функции допускается использование одной переменной (обозначается как x), скобок, числа пи (pi), экспоненты (e), математических операций: + — сложение, – — вычитание, * — умножение, / — деление, ^ — возведение в степень.
Допускаются также следующие функции: sqrt — квадратный корень, exp — e в указанной степени, lb — логарифм по основанию 2, lg — логарифм по основанию 10, ln — натуральный логарифм (по основанию e), sin — синус, cos — косинус, tg — тангенс, ctg — котангенс, sec — секанс, cosec — косеканс, arcsin — арксинус, arccos — арккосинус, arctg — арктангенс, arcctg — арккотангенс, arcsec — арксеканс, arccosec — арккосеканс, versin — версинус, vercos — коверсинус, haversin — гаверсинус, exsec— экссеканс, excsc — экскосеканс, sh — гиперболический синус, ch — гиперболический косинус, th — гиперболический тангенс, cth — гиперболический котангенс, sech — гиперболический секанс, csch — гиперболический косеканс, abs — абсолютное значение (модуль), sgn — сигнум (знак), logP — логарифм по основанию P, например log7(x) — логарифм по основанию 7, rootP — корень степени P, например root3(x) — кубический корень.

Производная дроби с переменной произвольной степени в знаменателе

( 1 / x с )’ = – c / x с+1

Пример нахождения производной дроби:
( 1 / x 2 )’ = – 2 / x 3 .

(впереди ставим минус, показатель степени переменной поднимаем в числитель дроби, а степень переменной в знаменателе увеличиваем на единичку. Немного “ненаучно”, но подходит для быстрого запоминания)

1-ый способ

То есть вначале производная берется как от степенной функции, а потом как от показательной.

Порядок следования слагаемых неважен: можно вначале взять производную от показательной функции, а затем как от степенной, так как от перестановки слагаемых сумма не меняется:

Задание. Найти производную функции

Решение. Применяем формулу. В рассматриваемом случае

Ответ.

Производные простых функций

1. Производная от числа равна нулю
с´ = 0
Пример:
5´ = 0

Откуда следует, что
(cx + b)’ = c
то есть дифференциал линейной функции y=kx+b равен угловому коэффициенту наклона прямой (k).

4. Производная переменной по модулю равна частному этой переменной к ее модулю
|x|’ = x / |x| при условии, что х ≠ 0
Пояснение:
Поскольку производная переменной (см. формулу 2) равна единице, то производная модуля отличается лишь тем, что значение скорости изменения функции меняется на противоположное при пересечении точки начала координат (попробуйте нарисовать график функции y = |x| и убедитесь в этом сами. Именно такое значение и возвращает выражение x / |x| . Когда x 0 – единице. То есть при отрицательных значениях переменной х при каждом увеличении изменении аргумента значение функции уменьшается на точно такое же значение, а при положительных – наоборот, возрастает, но точно на такое же значение.
5. Производная переменной в степени равна произведению числа этой степени и переменной в степени, уменьшенной на единицу
( x c )’= cx c-1 , при условии, что x c и сx c-1 ,определены а с ≠ 0
Пример:
(x 2 )’ = 2x
(x 3 )’ = 3x 2
Для запоминания формулы:
Снесите степень переменной “вниз” как множитель, а потом уменьшите саму степень на единицу. Например, для x 2 – двойка оказалась впереди икса, а потом уменьшенная степень (2-1=1) просто дала нам 2х. То же самое произошло для x 3 – тройку “спускаем вниз”, уменьшаем ее на единицу и вместо куба имеем квадрат, то есть 3x 2 . Немного “не научно”, но очень просто запомнить.
6. Производная дроби 1/х
(1/х)’ = – 1 / x 2
Пример:
Поскольку дробь можно представить как возведение в отрицательную степень
(1/x)’ = (x -1 )’ , тогда можно применить формулу из правила 5 таблицы производных
(x -1 )’ = -1x -2 = – 1 / х 2
7. Производная дроби с переменной произвольной степени в знаменателе
( 1 / x c )’ = – c / x c+1
Пример:
( 1 / x 2 )’ = – 2 / x 3
8. Производная корня (производная переменной под квадратным корнем)
( √x )’ = 1 / ( 2√x ) или 1/2 х -1/2
Пример:
( √x )’ = ( х 1/2 )’ значит можно применить формулу из правила 5
( х 1/2 )’ = 1/2 х -1/2 = 1 / (2√х)
9. Производная переменной под корнем произвольной степени
( n √x )’ = 1 / ( n n √x n-1 )
.

Вычисление производной

Вычисление производной — дело нехитрое, достаточно знать несколько простых правил и формулы дифференцирования простых функций; сложнее в этом онлайн калькуляторе было сделать интерпретатор математических выражений и алгоритм упрощения полученного результата, но об этом как-нибудь в другой раз…

Производная степенной функции (степени и корни)

Основные формулы

Производная от x в степени a равна a , умноженному на x в степени a минус один:
(1) .

Производная от корня степени n из x в степени m равна:
(2) .

Вывод формулы производной степенной функции

Случай x > 0

Рассмотрим степенную функцию от переменной x с показателем степени a :
(3) .
Здесь a является произвольным действительным числом. Сначала рассмотрим случай .

Чтобы найти производную функции (3), воспользуемся свойствами степенной функции и преобразуем ее к следующему виду:
.

Вывод формулы производной от корня степени n из x в степени m

Теперь рассмотрим функцию, являющуюся корнем следующего вида:
(4) .

Чтобы найти производную, преобразуем корень к степенной функции:
.
Сравнивая с формулой (3) мы видим, что
.
Тогда
.

На практике нет необходимости запоминать формулу (2). Гораздо удобнее сначала преобразовать корни к степенным функциям, а затем находить их производные, применяя формулу (1) (см. примеры в конце страницы).

Случай x = 0

Если , то степенная функция определена и при значении переменной x = 0 . Найдем производную функции (3) при x = 0 . Для этого воспользуемся определением производной:
.

Подставим x = 0 :
.
При этом под производной мы понимаем правосторонний предел, для которого .

Итак, мы нашли:
.
Отсюда видно, что при , .
При , .
При , .
Этот результат получается и по формуле (1):
(1) .
Поэтому формула (1) справедлива и при x = 0 .

Случай x .
При некоторых значениях постоянной a , она определена и при отрицательных значениях переменной x . А именно, пусть a будет рациональным числом. Тогда его можно представить в виде несократимой дроби:
,
где m и n – целые числа, не имеющие общего делителя.

Если n нечетное, то степенная функция определена и при отрицательных значениях переменной x . Например, при n = 3 и m = 1 мы имеем кубический корень из x :
.
Он определен и при отрицательных значениях переменной x .

Найдем производную степенной функции (3) при и при рациональных значениях постоянной a , для которых она определена. Для этого представим x в следующем виде:
.
Тогда ,
.
Находим производную, вынося постоянную за знак производной и применяя правило дифференцирования сложной функции:

.
Здесь . Но
.
Поскольку , то
.
Тогда
.
То есть формула (1) справедлива и при :
(1) .

Производные высших порядков

Теперь найдем производные высших порядков от степенной функции
(3) .
Производную первого порядка мы уже нашли:
.

Вынося постоянную a за знак производной, находим производную второго порядка:
.
Аналогичным образом находим производные третьего и четвертого порядков:
;

.

Отсюда видно, что производная произвольного n-го порядка имеет следующий вид:
.

Заметим, что если a является натуральным числом, , то n -я производная является постоянной:
.
Тогда все последующие производные равны нулю:
,
при .

Примеры вычисления производных

Пример

Найдите производную функции:
.

Преобразуем корни к степеням:
;
.
Тогда исходная функция приобретает вид:
.

Находим производные степеней:
;
.
Производная постоянной равна нулю:
.

Еще примеры

Найти производные следующих функций, зависящих от переменной x :
Решение > > > Решение > > > Решение > > > Решение > > > Решение > > >

Найти производную шестого порядка следующей функции:
.
Решение > > >

Автор: Олег Одинцов . Опубликовано: 09-04-2017

Производная показательной функции

Формула

Производная показательной функции равна произведению этой функции на натуральный логарифм основания степени.

Заметим, что если аргумент у показательной функции есть сложная функция (то есть там стоит более сложное выражение, чем просто $x$), то производную нужно находить по следующей формуле:

Примеры вычисления производной показательной функции

Задание. Найти производную функции $y(x)=2_$

Решение. Согласно формуле имеем:

Ответ. $y^(x)=2^ ln 2$