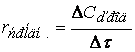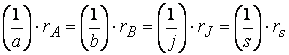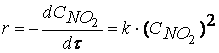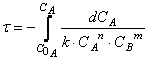Интегрирование кинетических уравнений в дифференциальной форме различных порядков

Кинетическое уравнение реакции — эмпирический закон, по которому скорость данной реакции зависит от состава реакционной смеси. Из него интегрированием может быть получена зависимость концентраций участников реакции от времени. Такую зависимость называют уравнением кинетической кривой. Фактически при экспериментальном изучении реакций имеют дело именно с такими зависимостями и из них выводят уравнения скорости. Методы, которые при этом применяются, обсуждаются в следующем разделе, а здесь рассмотрим интегрирование некоторых простых кинетических уравнений.

Предположим сначала, что скорость реакции зависит от концентрации только одного исходного вещества А с порядком а: м> = /с[А] а . Запишем уравнение скорости:

Для интегрирования разделим переменные в этом уравнении. То есть преобразуем его так, чтобы переменные, по которым следует интегрировать, были собраны в правой и левой частях уравнения отдельно:

Результат интегрирования правой части уравнения очевиден. Для интегрирования левой части вспомним из математики, что

где С — константа интегрирования.

Поэтому интегрирование (12.13) дает для любого порядка ос кроме первого:

а для первого порядка:

Обозначим [А]₀ концентрацию А в момент времени Г = 0. Подставим это в (12.14) и (12.15) и получим:

Эти уравнения линейные относительно времени. Поэтому они часто применяются при обработке экспериментальных данных. Из них можно получить уравнения явной зависимости концентрации от времени (собственно уравнения кинетических кривых). В частности, для уравнения скорости нулевого порядка м? = к_Ат (12.146) следует:

Это уравнение кинетической кривой нулевого порядка.

Для уравнения первого порядка м> = /с_а[А] уравнение (12.156) дает:

Это уравнение кинетической кривой первого порядка.

Для уравнения скорости второго порядка = /:_а[А] 2 уравнение (12.14б) принимает вид:

|

Аналогичные уравнения можно получить для любых других порядков.

Все кинетические кривые, представляющие зависимость концентрации исходного вещества от времени, являются убывающими, но различаются кривизной. Их не имеет смысла сравнивать между собой с точки зрения «быстроты реакции». Для целей сравнения обычно применяют время полупревращения реакции. Так называют время, за которое концентрация исходного вещества уменьшается вдвое. Оно обозначается /_1/2. Выражения для него можно получить из (12.14б) и (12.15б), приняв Г = /_1/2 и [А] = [А]₀/2:

Как видно, время /_1/2 всегда обратно пропорционально коэффициенту скорости. При уменьшении начальной концентрации оно уменьшается у реакций с порядком а 1 и не зависит от начальной концентрации у реакций первого порядка. Эту закономерность иллюстрирует рис. 12.2. На нем сопоставлены кинетические кривые нулевого, первого и второго порядков (при произвольной начальной концентрации 1 моль • дм -3 ). Для нулевого порядка из (12.20а) следует /_1/2 = [А]₀/2к_А. Поэтому последовательные интервалы времени, на которых происходит уменьшение концентрации в 2 раза, тем меньше, чем меньше исходная концентрация (рис. 12.2, а). Для реакции второго порядка из (12.20а) следует /_1/2 = 1/([А]₀&_а). Поэтому последовательные интервалы времени полупревращений увеличиваются при уменьшении концентрации (рис. 12.2, в). У реакции первого порядка время полупревращения не зависит от текущей концентрации (рис. 12.2, б).

Рис. 12.2. Кинетические кривые и интервалы времени полупревращения при разных порядках реакции с одним исходным веществом А

Интегрирование кинетических уравнений с двумя или более участниками реакций более трудоемко. Мы рассмотрим коротко только два наиболее простых случая.

Пусть кинетическое уравнение имеет вид:

Для его интегрирования следует учесть, что концентрации исходных веществ А и В связаны между собой через химическую переменную по (12.3). Отношение ^/У в химической кинетике обозначают х. (Оно не имеет специального названия.) С этим обозначением соотношение (12.3) для исходных веществ А и В записывается так:

Из этого следует: [А] = [А]₀ — ах и [В] = [В]₀ — Ьх. Подставим в (12.21):

Для интегрирования левой части уравнения можно обратиться к таблицам интегралов или к компьютеру с подходящим программным обеспечением (подходят символьные программы, такие как Мшкетайса и МмксасГ). По-другому ее можно преобразовать в сумму частных дробей, после чего она интегрируется без труда. Результат интегрирования для случая ос = (3 = 1 (общий порядок второй) и ?[А]₀ ф й[В]₀ имеет вид:

а его линейная форма (относительно времени):

Эти уравнения отличаются от уравнений с одним участником реакции тем, что содержат стехиометрические коэффициенты и две переменные концентрации. В действительности только начальные концентрации являются независимыми (произвольными), а текущие концентрации связаны между собой через них. Это видно из соотношения (12.22). Из него можно выразить [В] через [А] или наоборот. А именно: [В] = 1В]₀ — (?/д)([А]₀— [А]) в уравнениях (12.23).

Интегрированные уравнения более высоких порядков с двумя исходными веществами еще более громоздки. С другой стороны, для односторонних реакций со сложными кинетическими уравнениями часто оказывается возможным подобрать такие частные условия их проведения, при которых уравнение сводится к простому типу = &[А] а . Эта возможность широко используется в экспериментальной практике.

Для этого есть два приема. По одному из них начальную концентрацию одного из участников реакции выбирают намного большей, чем концентрация другого. В предыдущем разделе это условие уже упоминалось в связи с псевдопорядком реакции. Теперь этот прием можно проанализировать на примере уравнения кинетической кривой (12.23) для уравнения скорости = ?[А][В]. Если [В]₀ » [А] о и отношение Ь/а не слишком велико (как обычно в стехиометрических уравнениях), то можно принять (Ь/а)[А]₀ — [В]₀ = —[В]₀ в уравнениях (12.23). Кроме того, для этих условий из (12.22) следует [В] « [В]₀. Поэтому (12.23) преобразуется к виду:

Получилось уравнение, аналогичное кинетическому уравнению первого порядка (12.17), в котором коэффициент к’ = &[В]₀ — коэффициент скорости псевдопервого порядка. Разумеется, этот прием может применяться к уравнениям с любыми порядками.

Согласно другому приему можно выбрать начальные концентрации исходных веществ в стехиометрическом отношении. Например, для реакции (аА + ЬВ = продукты) с уравнением скорости = &[А] а [В] р можно выбрать [В]₀ = (Ь/а)[А]₀. Из (12.22) следует в этом случае, что текущие концентрации должны быть в постоянном отношении в ходе реакции, так как [В] = (Ь/а)[А]. Если подставить это в кинетическое уравнение, то получится:

где к’ = (Ь/а)^к — постоянная величина. В частности, для реакции (А + В = продукты) коэффициенты аиЬ равны, а поэтому к’ = к.

Таким образом, если в уравнение скорости входит произведение концентраций нескольких исходных веществ, но их начальные концентрации выбраны в стехиометрических отношениях, то уравнение упрощается до типа, содержащего концентрацию только одного участника реакции, причем порядок по нему равен общему порядку реакции.

В заключение этого раздела рассмотрим самое простое уравнение скорости двусторонней реакции = &[А] — к'[Ц, где А — исходное вещество, а Ъ — продукт. Концентрации этих веществ связаны соотношением, аналогичным (12.22). Из него следует [А] = [А]₀ — ах и [Т] = [г]₀ + гх. Поэтому уравнение скорости можно переписать в виде:

Интегрирование этого уравнения дает:

Это уравнение обычно относится к реакциям А концентрация исходного вещества стремится не к нулю, а к равновесному значению, зависящему от отношения к/к’ и от начальных концентраций. Для реагента А оно равно коэффициенту перед фигурными скобками в (12.27), потому что экспоненциальная функция стремится к 0 при /? —»°о, а выражение в скобках стремится к 1. Поэтому эти уравнения можно переписать, например (12.27в):

где [А]^ — концентрация А при ? —» .

Рисунок 12.3, а и б иллюстрирует поведение кинетических кривых для частных условий [А]₀ = 1 моль • дм -3 , [2]₀ = 0 при а = I = 1 и при отношениях к/к’ = 2/20. Как видно, чем больше отношение к/к’, тем больше походят эти кинетические кривые на обычные кривые, которые рассматривались ранее для односторонних реакций. Действи-

Рис. 12.3. Кинетические кривые исходного вещества и продукта в двусторонних реакциях со стехиометрией А г тельно, если к » к’ и [2]₀ = 0, то в (2.21a) можно принять ак + гк’

ак (при обычных стехиометрических коэффициентах). В результате уравнение (2.21a) преобразуется в уравнение кинетической кривой односторонней реакции первого порядка (12.17):

Следует заметить, что понятие времени полупревращения обычно не применяется к реакциям, кинетические уравнения которых содержат концентрации двух или более реагентов.

Видео:5 2 Кинетические уравненияСкачать

Кинетические уравнения реакций нулевого, первого и второго порядков

Изучение кинетики конкретных химических реакций обычно начинается с построения экспериментально определяемых кинетических кривых С _<= /(?) для реакции

Из рис. 12.1 ясно, что кривые отражают тот факт, что концентрация реагента А с течением времени уменьшается, а концентрация продукта В растет. На графике к кривой С_Л = /(?) проведены касательные, и в соответствии с определением скорости химической реакции тангенс угла а характеризует скорость реакции в момент 1_Х. Очевидно, что

Рис. 12.1. Кинетические кривые реакции (12.2)

Далее начинаются анализ этих данных и изучение механизма протекания реакции. Но это требует длительных и сложных исследований, поэтому, после того как получены кинетические кривые, можно обработать эти данные по кинетическим уравнениям закона Гульдберга и Вааге.

Реакция нулевого порядка. В случае если показатель степени в уравнении закона Гульдберга и Вааге равен нулю, описываемую таким уравнением реакцию называют реакцией нулевого порядка. По физическому смыслу это означает, что скорость такой реакции постоянна и не зависит от текущей концентрации реагента. Такое возможно, если поступление реагента в зону химической реакции постоянно и неизменно. На практике это реализуется, например, для реакции гидрирования этилена на платиновом катализаторе. Кинетическое уравнение реакции нулевого порядка имеет вид

Это дифференциальное уравнение пулевого порядка с разделяющимися переменными. В результате интегрирования получаем несколько важных зависимостей.

Зависимость концентрации от времени: где С_Ао — начальная; С_А — текущая концентрации реагента А.

Время, необходимое для достижения заданной концентрации:

Важной кинетической характеристикой является время полупревращения ?, ,₂ — время, в течение которого вступит в реакцию половина первоначально взятого вещества:

Константа скорости — величина размерная. Для реакции нулевого порядка ее размерность [моль л-Г 1 ]. В зависимости от природы реагирующих веществ время измеряется в секундах, минутах, часах и т.д.

Реакция первого порядка. В случае если показатель степени в уравнении закона Гульдберга и Вааге равен единице, описываемую таким уравнением реакцию называют реакцией первого порядка. Например, это реакции изомеризации

Кинетическое уравнение реакции первого порядка имеет вид

Это дифференциальное уравнение первого порядка с разделяющимися переменными. Его решение приводит к следующим результатам.

Зависимость концентрации от времени:

Время, необходимое для достижения заданной концентрации:

Время полупревращения:

Подстановка выражения для текущей концентрации в уравнение для скорости процесса приводит к экспоненциальной зависимости:

Для реакции первого порядка размерность константы скорости [? 1 ] и в зависимости от природы реагирующих веществ она измеряется в обратных секундах, минутах и г.д.

Значение константы скорости можно экспериментально получить из графика зависимости 1п С_А = С_л — &,/ (рис. 12.2).

Реакция второго порядка. Если общий порядок реакции (сумма показателей степени в уравнении закона Гульдберга и Вааге) равен двум, описываемую таким уравнением реакцию называют реакцией второго порядка, например реакция

В общем случае кинетическое уравнение реакции второго порядка имеет вид

В простейшем случае, когда реакция имеет вид 2А = D, решение кинетического уравнения приводит к выражению

или

Время полупревращения

Для реакций второго порядка величина обратной концентрации линейно возрастает со временем. Размерность константы скорости k₂ — [л ? моль» 1 •с 1 ].

В общем виде (при С_А ^ С_В(>) связь начальных и текущих концентраций реагентов А и В в ходе протекания химической реакции второго порядка имеет вид

Приведенные кинетические уравнения относятся к формальному этапу кинетических исследований (табл. 12.1). При изучении элементарных стадий их порядок может быть другим. Для определения порядка реакции строят график зависимости 1пгот Inc. Он линеен, и тангенс угла наклона равен порядку реакции. Для определения константы скорости строят график зависимости скорости от концентрации в степени п. Он также линеен, а тангенс угла наклона равен константе скорости реакции.

Если рассматривать элементарный акт химической реакции, то становится очевидным, что всякое взаимодействие — это реакция второго порядка. Во взаимодействии обязательно должны присутствовать два контрагента. В химии это означает, что всякое «первичное взаимодействие», изменяющее энергию частицы, должно являться взаимодействием ее нуклидо-электронной системы с электромагнитным квантом, поглощаемым этой системой и переводящим се в реакционно-способное состояние. Поэтому спектр и плотность квантовой среды,

Кинетические уравнения реакций различных типов

Видео:Физическая химия #3. Первый, второй и третий порядки химической реакции. Времена полупревращенияСкачать

Д.Г.НАРЫШКИН

Видео:Кинетика | Реакции 1-го порядка | Олимпиадные задачи по химииСкачать

КИНЕТИКА ХИМИЧЕСКИХ РЕАКЦИЙ

Возможности компьютерной математики

при исследовании поведения химических систем во времени

МОСКОВСКИЙ ЭНЕРГЕТИЧЕСКИЙ ИНСТИТУТТУ)

Видео:12.12 Приближенные методы кинетикиСкачать

ВВЕДЕНИЕ 3

Видео:Определение порядка реакции методом подбора кинетического уравненияСкачать

1. ОБЩИЕ ЗАКОНОМЕРНОСТИ ХИМИЧЕСКОЙ КИНЕТИКИ

Видео:Химическая кинетика. Формальная кинетика простых гомогенных реакций в закрытых системахСкачать

1.1. Скорость реакции

Видео:Составляем кинетические уравненияСкачать

1.2. Влияние концентрации на скорость реакции

Видео:Лукьяненко Д. В. - Дифференциальные уравнения - Лекция 1Скачать

1.3. Молекулярность и порядок реакции

1.4. Прямая и обратная задача химической кинетики

Видео:Дифференциальные уравнения в химической кинетике — решаем в пакете компьютерной алгебры MaximaСкачать

1.5. Реакция первого порядка

1.6. Реакции второго порядка

Видео:Порядок реакцииСкачать

1.7. Реакции других порядков

Видео:Выводим уравнение кинетической кривой реакции первого порядка без интегралов! || Кинетика || ХимияСкачать

1.8. Методы определения порядка реакции

Видео:Коробов М. В. - Физическая химия II - Кинетика необратимой реакции нулевого порядка и порядка nСкачать

2. Сложные реакции

Видео:Кинетика. Лекция 1 | Физ-кол. химияСкачать

2.1. Кинетика обратимых реакций

Видео:Кинетика || Лекция 4 || Реакции второго порядка, общий интеграл кинетического уравненияСкачать

2.2 Параллельные реакции

Видео:12.12 Химическая кинетикаСкачать

2.3 Последовательные реакции

Видео:Химическая кинетика I. Порядок реакции.Скачать

2.4 Метод квазистационарных концентраций

Видео:ЛЕКЦИЯ №4 || Химическая кинетика || Методы определения порядка реакцииСкачать

3. ВЛИЯНИЕ ТЕМПЕРАТУРЫ НА СКОРОСТЬ ХИМИЧЕСКИХ РЕАКЦИЙ

Видео:Влияние концентрации на скорость химических реакций. 10 класс.Скачать

3.1.Уравнение Аррениуса

Видео:Дифференциальные уравнения, 1 урок, Дифференциальные уравнения. Основные понятияСкачать

3.2. Связь энергии активации с тепловым эффектом реакции

Видео:Успенская И. А. - Химическая термодинамика и кинетика - Кинетика химических реакцийСкачать

3.3. Связь между скоростью реакции и равновесием

4. КИНЕТИКА ГЕТЕРОГЕННЫХ РЕАКЦИЙ

4.1. Общие понятия

4.2. Макрокинетика. Внешнедиффузионная область

4.3. Макрокинетика. Внутридиффузионное торможение

5. КИНЕТИКА РЕАКЦИЙ В ОТКРЫТЫХ СИСТЕМА

5.1. Химические реакторы.

5.2. Реакторы идеального смешения.

5.3. Реакторы идеального вытеснения.

5.4. Обратимые химические реакции в реакторах

в реакторах смешения и вытеснения.

7. Заключение

8. Рекомендуемая литература

ВВЕДЕНИЕ

Термодинамический метод изучения химических реакций позволяет сделать вывод о принципиальной возможности исследуемого процесса в тех или иных условиях и о глубине его протекания.

При постоянстве давления и температуры самопроизвольное протекание процесса возможно только в направлении уменьшения энергии Гиббса.

Условие определяет принципиальную возможность проведения процесса в заданных условиях из начального состояния в конечное, но не позволяет оценить скорость такого перехода.

Это обстоятельство связано с тем, что реакции не зависит от пути (механизма) процесса, а определяется только начальным и конечным состоянием системы.

Однако химические реакции могут протекать с самыми различными скоростями – от взрывных до очень медленных, протекающих в течение многих месяцев и лет. Даже одна и та же реакция, протекающая на различных катализаторах, может иметь скорости, различающиеся во много раз.

В некоторых случаях необходимо увеличить скорость реакции, в других наоборот, уменьшить. Таких примеров можно привести множество.

Поэтому изучение скорости протекания химических процессов (а это и составляет задачу кинетики) чрезвычайно важно.

Для рационального проведения химических реакций необходимо уметь управлять ими, знать зависимости скорости от различных параметров.

По кинетике издано очень много учебной и методической литературы. Но все эти книги и учебные пособия написаны так, что хочется спросить: «Какое, милые, тысячелетье на дворе?»

Современные системы компьютерной математики позволяют дать быстрый, и что, пожалуй, главное, наглядный прогноз относительно поведения химической системы во времени.

Однако в русскоязычной учебной литературе по кинетике химических реакций подход, в котором используются средства символьной математики в совокупности со средствами решения систем дифференциальных уравнений, представляемые математическим пакетом Mathcad , практически отсутствует.

Поэтому, отвечая на естественный вопрос – чем предлагаемое учебное пособие отличается от множества других, можно ответить: настоящее пособие имеет цель продемонстрировать эффективность применения математического пакета Mathcad для решения задач химической кинетики.

Специальные химические дисциплины, такие как термодинамика и кинетика, достаточно математизированы, и часто решение химической задачи вызывает у студентов значительные трудности, связанные с математикой – довольно часто это приводит к тому, что приходится сознательно упрощать задачу.

Пособие иллюстрирует богатейшие возможности, которые открывает применение компьютерной математики перед исследователем для анализа поведения химических систем во времени.

В этом отношении математические пакеты становятся практически незаменимыми элементами обучения, позволяющими сделать акцент на содержательном анализе полученных результатов.

Знаком >>>>>> в тексте пособия отмечен переход к Mathcad документу для интерактивного расчета.

1. ОБЩИЕ ЗАКОНОМЕРНОСТИ ХИМИЧЕСКОЙ КИНЕТИКИ

1.1. Скорость реакции

Х имическая кинетика – наука о скоростях и закономерно-стях протекания химических процессов во времени.

Химическая кинетика изучает механизм протекания процесса, т.е. те промежуточные стадии, состоящие из элементарных актов, через которые система переходит из начального состояния в конечное.

Химическая кинетика изучает скорости этих стадий и факторы, влияющие на их скорость.

Уравнение химической реакции показывает начальное состояние системы (исходные вещества) и её конечное состояние (продукты реакции), но не отражает механизма процесса. Однако путь перехода системы из начального в конечное состояние может быть достаточно сложным и «извилистым».
Так, например, реакция

протекает по следующему механизму:

Изучить кинетику реакции – значит показать, как реально протекает исследуемая реакция, её механизм, получить зависимость, связывающую скорость реакции с факторами, влияющими на неё.

Различают два типа химических реакций: гомогенные и гетерогенные.

К гомогенным относят реакции, у которых и исходные вещества и продукты реакции находятся в одной фазе. Взаимодействие веществ в таких реакциях происходит по всему объёму.

К гетерогенным реакциям относят реакции, протекающие на границе раздела фаз.

Пусть протекает реакция

(1.1)

где a ₁ , a ₂ , a_i , b ₁ , b ₂ , b_j – стехиометрические коэффициенты.

Скорость реакции по i –му веществу в гомогенной системе определяется как количество i -го вещества, образующееся (или реагирующее) в единице реакционного объёма в единицу времени:

(1.2)

где V – объём реакционной зоны, N_i – количество i –го вещества.

Если реакция протекает изохорически, т.е. объём во время реакции не меняется, то, поскольку концентрация и объём связаны соотношением

,

скорость реакции можно определить как изменение концентрации вещества во времени

Ранее мы определили скорость химической реакции как изменение числа молей реагирующих веществ в единицу времени в единице объема, т. е.

где — изменение числа молей одного из исходных веществ за время _.

Таким образом определяется средняя скорость реакции для заданного интервала времени.

Если объем в процессе реакции постоянен, то

где — изменение концентрации.

или

(скорость всегда положительна, а может быть больше или меньше нуля в зависимости от того, изменение концентрации исходного вещества или продукта реакции мы рассматриваем).

Если интервал времени , то мы получим истинную скорость реакции r в данный момент времени, т. е.

(1.3)

Размерность скорости: моль/(л·с).

Не только знак, но и абсолютное значение скорости зависит от того, по какому из участников реакции она измерена.

Так, например, при протекании реакции

скорость, с которой уменьшается концентрация водорода во время процесса, в три раза больше скорости убывания концентрации азота и в полтора раза выше скорости возрастания концентрации аммиака.

Следовательно, для реакции

скорости по компонентам реакции будут связаны соотношением:

Экспериментально установлено, что скорость реакции зависит от природы реагирующих веществ, их концентрации (или давления), температуры, т.е.

Раскрытие этой зависимости и составляет одну из задач кинетики.

1.2. Влияние концентрации на скорость реакции

Подход к выяснению зависимости скорости реакции от концентрации реагирующих веществ можно иллюстрировать следующим положением теории вероятностей: вероятность одновременного осуществления независимых событий равна произведению вероятностей каждого из них.

Для того чтобы произошло химическое взаимодействие, например, реакция

необходимо, но не достаточно, столкновение реагирующих молекул А и В, т.е. одновременное нахождение их в определённой точке реакционного пространства.

Вероятность ω нахождения молекулы для каждого из веществ прямо пропорциональна количеству молекул в единице объёма, т.е. его концентрации:

, .

Тогда вероятность того, что обе молекулы будут одновременно находиться в одной точке пространства, т.е. что они столкнутся, равна

Но не все столкновения приведут к реакции, а лишь их некоторая доля α , величина которой зависит от температуры и природы веществ, поэтому скорость реакции

Постоянную k , не зависящую от концентрации и зави­ сящую только от температуры и природы реагирующих веществ, называют константой скорости реакции.

Численное значе­ ние k выражает скорость реакции, когда концентрации реагирующих веществ равны 1 моль/л.

Пусть протекает химическая реакция:

aA + bB + … → продукты.

Тогда зависимость скорости реакции от концентрации можно выразить соотношением

(1.4)

Полученное выражение называют законом действия масс.

1.3. Молекулярность и порядок реакции

Число молекул, вступающих в реакцию, определяют молекулярность реакции.

Так, если в реакцию вступает одна молекула, то такая реакция называется молекулярной реакцией. Если в реакции участвуют две молекулы (безразлично, одинаковые или нет), то такая реакция называется бимолекулярной. Встречаются также тримолекулярные реакции.

Реакции более высокой степени молекулярности крайне редки из–за малой вероятности одновременного столкновения большого числа молекул.

Поэтому большинство реакций протекают в несколько элементарных, простых стадий, в которых участвует небольшое число молекул.

Так, например, рассмотренная выше реакция

протекает по следующему механизму:

вторая стадия (медленная)

Определить такие стадии – значит определить механизм, или путь реакции.

Скорость всей реакции определяется скоростью её наиболее медленной стадии, которая и определяет механизм.

Поэтому закон действующих масс справедлив только для таких элементарных стадий.

Молекулярность реакции легко определить в случае простых реакций, протекающих в одну стадию. В большинстве же случаев довольно трудно найти молекулярность реакции.

Поэтому вводится понятие порядка реакции, который можно найти из кинетических уравнений, полученных экспериментально.

Порядок реакции по данному веществу равен степени, в которой концентрация данного вещества входит в уравнение скорости реакции.

Сумма показателей степеней, в которых концентрация всех исходных веществ входит уравнение скорости реакции, равна порядку реакции в целом. Порядок химической реакции по веществу совпадает со стехиометрическим коэффициентом реакции лишь в очень простых реакциях, например в реакции синтеза йодистого водорода:

Порядок этой реакции по водороду (первый) и йоду (первый) равны стехиометрическими коэффициентами, а общий порядок реакции (второй) равен сумме стехиометрических коэффициентов в уравнении скорости реакции

В подавляющем большинстве случаев порядок реакции по веществу отличается от стехиометрических коэффициентов уравнения реакции для этого вещества.

Соответственно общий порядок реакции обычно не равен сумме стехиометрических коэффициентов уравнения реакции.

при температурах, меньших 298К, протекает по следующему механизму:

первая стадия процесса: NO ₂ + NO ₂ ® NO ₃ + NO

вторая стадия процесса: NO ₃ + CO ® CO ₂ + NO _2,

причем лимитирующей, т.е. скорость определяющей стадией является первая стадия процесса:

Тогда, согласно первому постулату химической кинетики, который утверждает, что скорость всей реакции равна скорости его самой медленной стадии, можно записать:

,

где— скорость первой стадии процесса.

Согласно второму постулату химической кинетики, который утверждает, что скорость элементарной (одностадийной) реакции пропорциональна концентрации реагирующих веществ в степенях, равных стехиометрическим коэффициентам, получим зависимость скорости реакции

от концентрации реагирующих веществ:

Обратите внимание, что скорость реакции

не зависит от концентрации оксида углерода CO .

Уравнение, выражающее зависимость скорости реакции от концентрации каждого вещества, называют кинетическим уравнением реакции в дифференциальной форме.

К сожалению, кинетическое уравнение реакции может быть получено только при её экспериментальном изучении и не может быть выведено из стехиометрического уравнения.

1.4. Прямая и обратная задача химической кинетики

Определение на основании экспериментальных данных о зависимости концентраций от времени проведения процесса параметров кинетического уравнения – порядка реакции и значения константы скорости – составляет так называемую обратную задачу химической кинетики.

Знание кинетического уравнения реакции в дифференциальной форме позволяет определить время достижения некоторой заданной концентрации реагирующего вещества (или продукта реакции).

Пусть, например, протекает реакция

aA + bB + … → продукты,

кинетическое уравнение которой:

Тогда время достижения некоторой концентрации вещества А можно определить, интегрируя кинетическое уравнение реакции в дифференциальной форме:

Решая дифференциальное уравнение

можно получить зависимость концентрации реагирующего вещества (или продукта реакции) от времени проведения процесса – так называемых кинетических кривых.

Определение – на основании феноменологической модели процесса – концентраций реагентов от времени проведения реакции составляет прямую задачу химической кинетики.

Отметим сразу, что аналитически не всегда удаётся решить дифференциальное уравнение, особенно в случае сложной кинетики.

В этом случае прибегают к численным методам решения и использование компьютерной математики. В частности, применение математических пакетов, например, таких, как Mathcad , становится незаменимым инструментом в исследовательской практике и в процессе обучения.

1.5. Реакция первого порядка

Реакция первого порядка может быть записана в общем виде:

Примером такой реакции может служить реакция разложения диметилового эфира:

Кинетическое уравнение реакции первого порядка можно представить дифференциальным уравнением

(1.5)

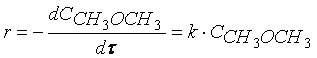
Тогда время t достижения некоторой концентрации диметилового эфира CH ₃ OCH ₃ можно определить, интегрируя соотношение (1.5):

,

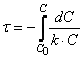
где С и C ₀ – концентрация CH ₃ OCH ₃ в момент времени t и t =0.

Интегрирование приводит к выражению

(1.6) И тогда зависимость концентрации исходного вещества CH ₃ OCH ₃ от времени проведения процесса:

. (1.7)

Из (1.7) следует, что концентрация исходного вещества со временем изменяется по экспоненциальному закону:

Проиллюстрируем изменение концентрации в зависимости от времени на примере реакции первого порядка

с начальной концентрацией моль/л и константой скорости при некоторой температуре k=0.05 1/c

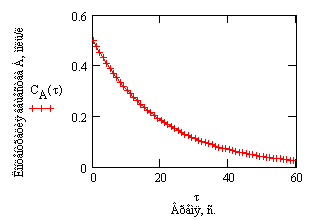
Рис.1. Зависимость концентрации

от времени в реакции первого порядка .

и, в логарифмических координатах, согласно зависимости