Как нарисовать прямую заданную уравнением

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Хочешь готовиться к экзаменам бесплатно? Репетитор онлайн бесплатно. Без шуток. ЗДЕСЬ

Для начала определимся с формулой прямой или линейной функции ее записывают по-разному, но смысл от этого не меняется:y=kx+b; y=ax+b; ax+by+c=0;

a и k — называются угловыми коэффициентами, а число b – свободным членом.

Если a>0 или k>0, то график прямой возрастающий;

y=ax+b, a>0

Если a a

Параллельные прямые имеют равные угловые коэффициенты и разные свободные члены b не равно с.
Пусть дано две прямые y=kx+b и y=ax+c, они будут параллельны если k=a

Признак параллельности прямых a=k

Перпендикулярные прямые (это прямые которые пересекаются под 90 градусов), произведение их угловых коэффициентов будет равняться -1.
Пусть дано две прямые y=kx+b и y=ax+c, они будут перпендикулярны если k*a=-1

Перпендикулярные прямые k*a=-1

b — указывает где график прямой пересекает ось y.

Алгоритм построения прямой.
Что бы построить прямую, нужно найти не менее двух то точек на графике и начертить линейную функцию.

ПРАКТИЧЕСКАЯ ЧАСТЬ

Рассмотрим на примере №1:

берем 2 точки чтобы построить график прямой
x1=0 y1=0+2=2 получили точку (0;2)
x2=1 y2=1+2=3 получили точку (1;3)

Видно что a=1 (график прямой возрастает),
b=2 (график прямой пересекает ось y в точке (0;2))

y=ax+b, a>0

Пример №2:
Среди прямых, заданных уравнениями, укажите пары параллельных прямых: 1) х+у=2; 2) у-х=2; 3) х-у=3; 4) y=1; 5) у=3; 6) 2х+2у+5=0.

Выразим во всех уравнениях y, получим
1) у=2-x; k=-1
2) у=2+x; k=1
3) у=x-3; k=1
4) y=1; k=0
5) у=3; k=0
6) у=-2,5-x; k=-1.

Ответ: Параллельные прямые 1) и 6); 2) и 3); 4) и 5), так как коэффициенты их равны.

Видео:Уравнение окружности (1)Скачать

Практика. Решение задач. Часть 1. Уравнения прямой

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

Мы изучили новые инструменты – координаты и действия с векторами в координатах, операцию скалярного умножения векторов. Этот урок мы посвятим решению задач и потренируемся применять эти новые инструменты на практике.

Видео:№959. Начертите окружность, заданную уравнением: а) х2+у2= 9Скачать

Построение прямой по ее уравнению

Прямая вполне определена, если известны две принадлежащие ей точки. Для того чтобы построить прямую по ее уравнению, надо, пользуясь этим уравнением, найти координаты двух ее точек. Твердо следует помнить, что если точка принадлежит прямой, то координаты этой точки удовлетворяют уравнению прямой.

При практическом построении прямой по ее уравнению наиболее точный график получится тогда, когда координаты взятых для ее построения двух точек — целые числа.

1. Если прямая определена общим уравнением Ax + By + C = 0 и , то для ее построения проще всего определить точки пересечения прямой с координатными осями.

Укажем, как определить координаты точек пересечения прямой с координатными осями. Координаты точки пересечения прямой с осью Ox находят из следующих соображений: ординаты всех точек, расположенных на оси Ox, равны нулю. В уравнении прямой полагают, что y равно нулю, и из полученного уравнения находят x. Найденное значение x и есть абсцисса точки пересечения прямой с осью Ox. Если окажется, что x = a, то координаты точки пересечения прямой с осью Ox будут (a, 0).

Чтобы определить координаты точки пересечения прямой с осью Oy, рассуждают так: абсциссы всех точек, расположенных на оси Oy, равны нулю. Взяв в уравнении прямой x равным нулю, из полученного уравнения определяют y. Найденное значение y и будет ординатой пересечения прямой с осью Oy. Если окажется, например, что y = b, то точка пересечения прямой с осью Oy имеет координаты (0, b).

Пример. Прямая 2x + y — 6 = 0 пересекает ось Ox в точке (3, 0). Действительно, взяв в этом уравнении y = 0, получим для определения x уравнение 2x — 6 = 0, откуда x = 3.

Чтобы определить точку пересечения этой прямой с осью Oy, положим в уравнении прямой x = 0. Получим уравнение y — 6 = 0, из которого следует, что y = 6. Таким образом, прямая пересекает координатные оси в точках (3, 0) и (0, 6).

Если же в общем уравнении прямой C = 0, то прямая, определяемая этим уравнением, проходит через начало координат. Таким образом, уже известна одна ее точка, и для построения прямой остается только найти еще одну ее точку. Абсциссу x этой точки задают произвольно, а ординату y находят из уравнения прямой.

Пример. Прямая 2x — 4y = 0 проходит через начало координат. Вторую точку прямой определим, взяв, например, x = 2. Тогда для определения y получаем уравнение 2*2 — 4y = 0; 4y = 4; y = 1. Итак, прямая 2x — 4y = 0 проходит через точки (0, 0) и (2, 1).

Если прямая задана уравнением y = kx + b с угловым коэффициентом, то из этого уравнения уже известна величина отрезка b, отсекаемого прямой на оси ординат, и для построения прямой остается определить координаты еще только одной точки, принадлежащей этой прямой. Если в уравнении y = kx + b , то легче всего определить координаты точки пересечения прямой с осью Ox. Выше было указано, как это сделать.

Если же в уравнении y = kx + b b = 0, то прямая проходит через начало координат, и тем самым уже известна одна принадлежащая ей точка. Чтобы найти еще одну точку, следует дать x любое значение и определить из уравнения прямой значение y, соответствующее этому значению x.

Пример. Прямая 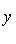проходит через начало координат и точку (2, 1), так как при x = 2 из ее уравнения .

Уравнение прямой, проходящей через данную точку в данном направлении. Уравнение прямой, проходящей через две данные точки. Угол между двумя прямыми. Условие параллельности и перпендикулярности двух прямых. Определение точки пересечения двух прямых

1. Уравнение прямой, проходящей через данную точку A(x₁, y₁) в данном направлении, определяемом угловым коэффициентом k,

Это уравнение определяет пучок прямых, проходящих через точку A(x₁, y₁), которая называется центром пучка.

2. Уравнение прямой, проходящей через две точки: A(x₁, y₁) и B(x₂, y₂), записывается так:

(2)

Угловой коэффициент прямой, проходящей через две данные точки, определяется по формуле

(3)

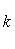
3. Углом между прямыми A и B называется угол, на который надо повернуть первую прямую A вокруг точки пересечения этих прямых против движения часовой стрелки до совпадения ее со второй прямой B. Если две прямые заданы уравнениями с угловым коэффициентом

то угол между ними определяется по формуле

(5)

Следует обратить внимание на то, что в числителе дроби из углового коэффициента второй прямой вычитается угловой коэффициент первой прямой.

Если уравнения прямой заданы в общем виде

угол между ними определяется по формуле

(7)

4. Условия параллельности двух прямых:

а) Если прямые заданы уравнениями (4) с угловым коэффициентом, то необходимое и достаточное условие их параллельности состоит в равенстве их угловых коэффициентов:

б) Для случая, когда прямые заданы уравнениями в общем виде (6), необходимое и достаточное условие их параллельности состоит в том, что коэффициенты при соответствующих текущих координатах в их уравнениях пропорциональны, т. е.

(9)

5. Условия перпендикулярности двух прямых:

а) В случае, когда прямые заданы уравнениями (4) с угловым коэффициентом, необходимое и достаточное условие их перпендикулярности заключается в том, что их угловые коэффициенты обратны по величине и противоположны по знаку, т. е.

(10)

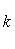
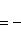
Это условие может быть записано также в виде

б) Если уравнения прямых заданы в общем виде (6), то условие их перпендикулярности (необходимое и достаточное) заключается в выполнении равенства

6. Координаты точки пересечения двух прямых находят, решая систему уравнений (6). Прямые (6) пересекаются в том и только в том случае, когда

💥 Видео

№978. Начертите прямую, заданную уравнением: а) у = 3; б) х = -2; в) у=-4; г) х = 7.Скачать

9 класс, 6 урок, Уравнение окружностиСкачать

Как построить график линейной функции.Скачать

Как построить прямую, заданную уравнением. Частные случаи уравнения прямой. Урок 2 Геометрия 8 классСкачать

Записать уравнение прямой параллельной или перпендикулярной данной.Скачать

9 класс, 7 урок, Уравнение прямойСкачать

Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Точки пересечения графика линейной функции с координатными осями. 7 класс.Скачать

Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать

Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать

Составляем уравнение прямой по точкамСкачать

Как построить график функции без таблицыСкачать

Аналитическая геометрия, 6 урок, Уравнение прямойСкачать

Математика без Ху!ни. Уравнение плоскости.Скачать

Линейная функция: краткие ответы на важные вопросы | Математика | TutorOnlineСкачать

Построить график ЛИНЕЙНОЙ функции и найти:Скачать

начертить окружность. Привести уравнение окружности к стандартному виду. Координаты центра и радиус.Скачать