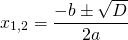Как написать уравнение в code

Видео:Уроки C++. Простые линейные уравненияСкачать

Уроки программирования, алгоритмы, статьи, исходники, примеры программ и полезные советы

ОСТОРОЖНО МОШЕННИКИ! В последнее время в социальных сетях участились случаи предложения помощи в написании программ от лиц, прикрывающихся сайтом vscode.ru. Мы никогда не пишем первыми и не размещаем никакие материалы в посторонних группах ВК. Для связи с нами используйте исключительно эти контакты: vscoderu@yandex.ru, https://vk.com/vscode

Видео:34 Задача: Найти корни квадратного уравнения при помощи PythonСкачать

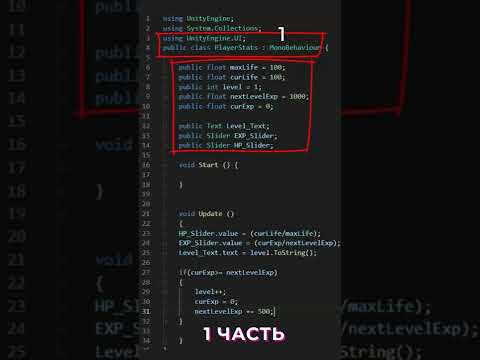
Решение квадратного уравнения на С# в Windows Forms.

Сегодня мы напишем программу, которая выведет нам решение квадратного уравнения на С#. Сделаем мы всё это в Windows Forms. В программе мы найдём дискриминант и оба корня.

Для создания программы нам понадобится знание начальной школы и трёх формул.

Формула нахождения дискриминанта:

Формула нахождения корней выражения, если дискриминант больше нуля:

И формула нахождения одного корня выражения, если дискриминант равен нулю:

Ну и, пожалуй, стоит вспомнить сам вид квадратного выражения:

Теперь пора приступать к программе.

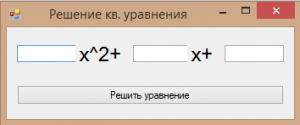
Для начала создаём незамысловатую форму под наши нужды:

Здесь у нас 3 TextBox’a, 2 Label’a и 1 кнопка Button. Выводить решение мы будем в отдельном MessageBox’е.

Приступаем к коду. Дважды щёлкаем на Button и в открывшемся участке кода начинаем писать.

Сначала объявляем переменные, которым будут присвоены значения,введённые пользователем в TextBox’ы:

Видео:Как писать простой кодСкачать

Программирование в уравнениях

В обычном, как императивном, так и функциональном программировании вся программа по большому счету сводится к огромному числу равенств x = . , где слева стоит переменная, а справа — выражение, зависящее от переменных. А языки программирования предоставляют синтаксический сахар, что бы записать это множество как можно более компактно. Это уже почти уравнения, только тривиальные.

Некоторые сложности обнаруживаются в ленивых языках:

Здесь fib присутствует и в левой и в правой части, то есть мы получаем полноценное уравнение, решением которого будет бесконечная последовательность чисел Фибоначчи. Так как на бесконечных последовательностях естественным образом определяется топология, Haskell может решить это уравнение методом проcтых итераций (через оператор неподвижной точки).

Еще дальше по пути уравнений пошел Prolog. Каждый предикат определяет уравнение на множествах, хоть и записывается без знака равенства. Решаются такие уравнения почти перебором и возможность использовать в них арифметику сильно ограничена.

Но есть язык, в котором уравнения являются важнейшей частью — это Modelica.

Здесь отрезок определяется как координаты концов и длинна, при этом длина и координаты связаны очевидным уравнением.

(К сожалению, source такого языка не знает, а вставить раскрашенный pygment-ом html не получается.)

Естественно, уравнения могут быть объединены в систему:

Здесь описывается манипулятор, состоящий из четырех соединенных шарнирами реек управляемый двумя сервоприводами.

Как следует из названия, Modelica предназначена для моделирования сложных, гетерогенных систем. Ее реализации есть у знаменитого Вольфрама, производителя САПР (не путать и «чертежными программами») CATIA. Есть также и свободные реализации, такие как OpenModelica.

Так как моделируемые объекты редко описываются алгебраическими уравнениями, Modelica умеет решать и обыкновенные дифференциальные уравнения. К сожалению, уравнения в частных производных она пока не осилила, но обычно можно разбить систему на конечные элементы и породить обыкновенные дифуры в цикле.

В качестве примера приведу модель очень сложной гибридной электромеханической системы — Гауссгана:

Здесь x — координата снаряда, v — напряжение, i — ток. Для отладки вычисляется полная энергия pe — ее график будет горизонтальной прямой.

Кроме текстового представления программы, в Modelica стандартизовано и графическое (хотя лично я предпочитаю работать с текстом). Для повторного использования кода применяется знакомое многим по ООП наследование. Есть обширные библиотеки по электротехнике, теплотехнике, механике и, даже, биохимии.

Разработчики «Моделик» не расчитывают охватить все одной системой — большинство реализаций допускает комоделирование с помощью Functional Mock-up Interface. При желании этот же интерфейс можно задействовать для взаимодействия с внешним миром, но это пока открытая область.

Видео:Python для самых маленьких. Линейные уравнения. Решение задачСкачать

Программа для решения квадратных уравнений на C++

Довольно часто в пособиях по программированию встречаются задания по нахождению решений каких-нибудь математических уравнений. Задача нахождения корней квадратного уравнения — это довольно тривиальная задача, как и многие другие задачи. Решается она очень просто при помощи листа бумаги и ручки, но решение можно автоматизировать посредством написания прикладной программы и её использования. В этой статье мы напишем такую программу.

Алгоритм решения квадратного уравнения

Многие знают, что уравнение вида ax 2 + bx + c = 0 , где a не равно 0, называют квадратным уравнением.

Существуют различные способы решения квадратных уравнений, но мы рассмотрим решение через дискриминант.

Обозначается дискриминант буквой D . Из школьного курса знаем, что D = b 2 — 4ac .

Существует несколько условий:

• Если D > 0, то решение имеет 2 различных вещественных корня.
• Если D = 0, то оба вещественных корня равны.
• Если D для вводавывода в консоли, #include для работы с математическими функциями и область using namespace std;

Просим пользователя ввести значения переменных и сохраняем каждое значение

Проверяем условие, если дискриминант больше или равен 0, то находим корни и выводим

в противном случае выводим сообщение

На этом всё, осталось скомпилировать, запустить и проверить. Запускаем и вводим данные, чтобы D был меньше 0

В этом случае D = 3*3 — 4*2*3 = -15, а это меньше 0, значит ответ программа дала верный.

Ответы тоже верны. Программа работает правильно.

Ниже представлен весь листинг программы для нахождения корней квадратного уравнения на C++

Для вас это может быть интересно:

Видео:решение (поиск корней) квадратных уравнений c++Скачать

Программа для решения квадратных уравнений на C++ : 24 комментария

Программировать так сложно…

1. Nicknixer Автор записи 15.10.2016

Не так сложно, как Вам кажется! Немного литературы, немного практики и смотреть на код решения такой задачи Вы будете по-другому.

Доброго времени суток! Помогите пожалуйста написать программу, которая считает сколько символов в ряде двумерного массива. То есть , например массив 5 на 5, сколько символов в 1 ряде, сколько во 2 и т.д.

Ответил вам по электронной почте

Критику принимаете? 🙂
Программа дырявая как сито.

Если число очень маленькое, но положительное, например 10^(-20) — у вас будет переполнение или типо того. Оператор > проверяет знак числа (это отдельный бит), а оператор == для дробных чисел не имеет смысла, т.к. в младших разрядах числа обычно находится какой-нибудь мусор, который при таком сравнении дает false.

x = ( -1*b + sqrt(b*b — 4*a*c) ) / (2 * a);
x = ( -1*b — sqrt(b*b — 4*a*c) ) / (2 * a);

Тут есть три вопроса:
1) зачем два раза вычислять одно и тоже (я про корень)
2) что делать если мне корни надо как-то использовать, а не просто вывести (тут есть проблема, ведь у меня то один корень — то два). Чтобы лучше понять в чем проблема — попробуйте вынести вычисление корней в отдельную функцию. У вас то вообще, если корень один — то их выведется все равно два, одинаковых.
3) в переменной «a» может быть ноль (или близкое к нулю число) — при этом мы получим деление на ноль (а точнее, переполнение).

Но это ведь еще не все. Что будет если и «a» и «b» равны нулю? — тебе надо рассмотреть два варианта — если c = 0 (условно, близко к нулю), то корней бесконечно много. А если c != 0, то корней нет.

Вообще, эта задача — прекрасный пример для юнит-тестирования и демонстрации принципов разработки через тестирование. Именно его я рассматривал в своей статье по теме тестирования: Юнит-тестирование. Пример. Boost Unit Test. Дело в том, что тут куча вариантов сделать ошибку, при этом их понимание приходит не сразу, т.е. школьник решая задачу напишет по формуле которой учили (ну и вот как у вас). А потом надо разбираться и смотреть как программа может сломаться, при этом разрабатывать тесты.

1. Николай Сергейчук Автор записи 09.02.2017

Принимаем 🙂
Согласен с вами во всём! Программу можно реализовать намного лучше, используя различные проверки и валидацию входных данных.
Однако, статья рассчитана на аудиторию, которая только начинает познавать программирование или делает лабораторную. 🙂 Чтобы людям легче было понять, реализация данной программы упрощена до невозможности. И, возможно, несправедливо было с моей стороны не предупредить их о возможных ошибках в работе программы, которые могут вскрыться позже, если подать на вход определенные значения.
Кстати, у вас интересная статья по тестированию!

Николай, доброго времени суток! Можете помочь с написанием програмки в с++? 1-1/2!+1/3!-1/4!+1/5! и так до 1/100! ? Чтобы при заднии в строке номера члена последовательности выдавал сумму до него по такой вот формуле? Буду очень благодарен!

Пожалуйста подскажите как ввести экран правильный ответ дискриминанта

Помогите решить в Dev C++
Sqrt x^2+1+sqrt|x|,x0

Здравствуйте, можете помочь с решением биквадратного и триквадратного уравнения?

#include
using namespace std;
int main()
<
/*Решение квадратных уравнений*/
setlocale(0, «»);
cout a;
cout b;
cout c;
D = pow(b, 2) — 4 * a * c;
cout

ну и? если даже тупо скопировать код и вставить его в cpp.sh , ничего не работает. поебота какая то этот с++

Уважаемая, Лена! Я, надеюсь, вы знаете, что код программы, написанной на языке программирования C++ нельзя тупо вставить в блокнот и сохранить под названием «cpp.sh»? Если не знали, то я, видимо, открыл для вас Америку!

помогите решить. заданы 3 перемены a.b.c записать вы радение на С
< 7a/b+2a, если a=b,
Х= b,
b и а не равно != с

iconcerts где забыл
#include

Я ради интереса написал программу нахождения корней квадратного уравнения на С++, с выводом корней как в десятичном виде, так и в виде простой дроби (причём уже сокращённой), потому что выводя корни в десятичном виде программа их одновременно сокращает и округляет и 1/3 превращается в 0.333333 хотя на самом деле 0.333333 (3), то есть для проверки правильно ли нашёл корни ваш ребёнок, вы с получите что-то типа: X1= 0.285714; X2=0.214286, а на самом деле это будет X1=2/7; X2=3/14, кроме того, если корень из дискриминанта не получается целым числом, вы уже получите двойную неточность: сначала при извлечении корня программа отсечёт значение до 4-6 цифр после запятой с округлением, а затем сделает то же самое при делении числителя на знаменатель. Я и здесь сделал вывод корней в двух значениях: в десятичном и в виде выражения X1= (-b + sqrt(D))/(2*a); X2= (-b — sqrt(D))/(2*a), то есть выводится примерно вот так X1=-5+sqrt(21)/2; X2=-5-sqrt(21)/2 с одновременным разложением дискриминанта под корнем на множители, вынесением этих множителей из-под корня, если они выносятся нацело, их перемножением и дальнейшим сокращением. Вот, например, имеем a=3, b=15, c=3, при решении получаем D=189 программа выдаёт десятичные корни X1= -0.208712 и X2= -4.79129, а в виде выражения имеем: X1= -5+sqrt(21)/2, то есть первоначально получаем: X1= -15+sqrt(189)/6, -> 189=21*9 -> -15+3sqrt(21)/6 далее идёт сокращение на 3 и итог -5+sqrt(21)/2

День добрый.
Недавно начал изучать C++. Решил попробовать написать решение квадратного уравнения именно через оператор вида «условие ? выполняется : не выполняется». Т.е. если условие выполняется, то имеем два решения (даже если d = 0, то тоже должно быть два решения x1 = x2), если d a;
std::cout b;
std::cout c;
d = pow(b, 2) — 4 * a*c;
d >= 0 ? xfst = ((-b + sqrt(d)) / double(2 * a)) , xscd = ((-b — sqrt(d)) / double(2 * a)) : std::cout

1. Николай Сергейчук Автор записи 12.02.2020

if (d >= 0) <
xfst = ((-b + sqrt(d)) / double(2 * a));
xscd = ((-b — sqrt(d)) / double(2 * a));
std::cout

Создать программу для решения квадратного уравнения.
У меня не получаеться, но и копифейсом я не хочу заниматься.
Прошу помогите. Заранее спасибо.

Здравствуйте! Как решить эту задачу? Приведенный пример сверху не подходит .

Давайте напишем действительно полезную программу! Вы наверняка уже устали считать дискриминант для квадратных уравнений? Давайте автоматизируем этот процесс.

На вход программы подаются три целых числа — коэффициенты уравнения ax^2 + bx + c = 0ax
2
+bx+c=0

Гарантируется, что a neq 0a

=0.

Выведите через пробел корни уравнения в порядке убывания и округленные «вниз». Если уравнение имеет корень кратности 2 — выведите одно число. Если у уравнения нет действительных корней — выведите «NO»

Для извлечения корней используйте функцию sqrt. Она содержится в библиотеке сmath ( она уже импортирована в коде ). Для округления воспользуйтесь функцией floor ( из той же библиотеки ).

1 0 -4
Sample Output 1:

2 -2
Sample Input 2:

1 2 2
Sample Output 2:

Пожалуйста подскажите как ввести экран ответ дискриминанта

Пожалуйста подскажите как ввести на екран ответь дискриминанта

Подскажите как правильно решить?
Обчислити z = (x1 + y1) / (x2 + y2), де х1, х2 — коренi рiвняння 2х^2 + x — 4 =0.
y1, y2 — коренi рiвняння ay^2 + 2y — 1 = 0. Усi коренi дiйснi.

using namespace std;

int main() <
double a = 2, b, c = -4;
int x1, x2;
double a1, b1 = 2, c1 = -1;
int y1, y2;
float z;

if((b*b — 4*a*c) >= 0 ) <
x1 = ( -1*b + sqrt(b*b — 4*a*c)) / (2 * a);
cout a1;

if((b1*b1 — 4*a1*c1) >= 0) <
y1 = ( -1*b1 + sqrt(b1*b1 — 4*a1*c1)) / (2 * a1);
cout = 0, y1 >= 0, y2 >= 0) <
z = (x1 + y1)/(x2 +y2);
cout

Добавить комментарий Отменить ответ

Этот сайт использует Akismet для борьбы со спамом. Узнайте, как обрабатываются ваши данные комментариев.

🎦 Видео

Не могу написать программу! Что делать! Как начать писать код!Скачать

Задача 411. Квадратное уравнение. acmp.ru C++Скачать

Уроки C++ с нуля🔥Решение математических задач на языке С++🔥Переменные в языке С++🔥Скачать

Урок 3. Изучаем Python. Запись математических выражений. Библиотека MathСкачать

Программа, определяющая корни квадратного уравнения. Язык программирования Python.Скачать

Математика это не ИсламСкачать

Python. Команды print() input()Скачать

ОПЕРАТОРЫ. АРИФМЕТИЧЕСКИЕ ОПЕРАЦИИ С ЧИСЛАМИ В C# | C# ОТ НОВИЧКА К ПРОФЕССИОНАЛУ | Урок # 8Скачать

Решение квадратного уравнения на C# для консоли Windows в Visual Studio 2022Скачать

#5. Математические функции и работа с модулем math | Python для начинающихСкачать

Топ 3 худших программиста на YouTube! #код #айти #программистСкачать

26 задания по теме генетический кодСкачать

Уроки C++ с нуля / Урок #17 - Математические операцииСкачать

9 класс, 7 урок, Уравнение прямойСкачать

Разнёс чужой код за 15 секунд. Часть 1 #код #айти #программирование #рефакторингСкачать