В этой статье и постараюсь объяснить 2 способа отбора корней в тригонометрическом уравнение: с помощью неравенств и с помощью тригонометрической окружности. Перейдем сразу к наглядному примеру и походу дела будем разбираться.
а) Решить уравнение sqrt(2)cos^2x=sin(Pi/2+x)
б) Найдите все корни этого уравнения, принадлежащие промежутку [-7Pi/2; -2Pi]
Решим пункт а.
Воспользуемся формулой приведения для синуса sin(Pi/2+x) = cos(x)
sqrt(2)cos^2x — cosx = 0
cosx(sqrt(2)cosx — 1) = 0
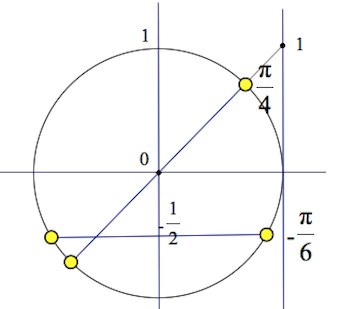
x1 = Pi/2 + Pin, n ∈ Z
sqrt(2)cosx — 1 = 0
x2 = arccos(sqrt(2)/2) + 2Pin, n ∈ Z
x3 = -arccos(sqrt(2)/2) + 2Pin, n ∈ Z
x2 = Pi/4 + 2Pin, n ∈ Z
x3 = -Pi/4 + 2Pin, n ∈ Z
Решим пункт б.
1) Отбор корней с помощью неравенств
Здесь все делается просто, полученные корни подставляем в заданный нам промежуток [-7Pi/2; -2Pi], находим целые значения для n.
-7Pi/2 меньше или равно Pi/2 + Pin меньше или равно -2Pi
Сразу делим все на Pi
-7/2 меньше или равно 1/2 + n меньше или равно -2
-7/2 — 1/2 меньше или равно n меньше или равно -2 — 1/2
-4 меньше или равно n меньше или равно -5/2
Целые n в этом промежутку это -4 и -3. Значит корни принадлежащие этому промежутку буду Pi/2 + Pi(-4) = -7Pi/2, Pi/2 + Pi(-3) = -5Pi/2
Аналогично делаем еще два неравенства
-7Pi/2 меньше или равно Pi/4 + 2Pin меньше или равно -2Pi
-15/8 меньше или равно n меньше или равно -9/8
Целых n в этом промежутке нет
-7Pi/2 меньше или равно -Pi/4 + 2Pin меньше или равно -2Pi
-13/8 меньше или равно n меньше или равно -7/8
Одно целое n в этом промежутку это -1. Значит отобранный корень на этом промежутку -Pi/4 + 2Pi*(-1) = -9Pi/4.
Значит ответ в пункте б: -7Pi/2, -5Pi/2, -9Pi/4
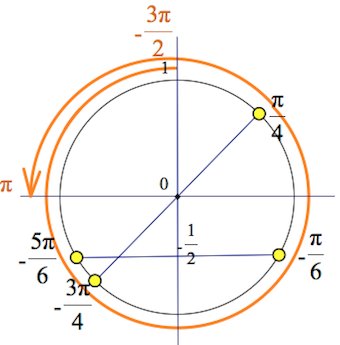
2) Отбор корней с помощью тригонометрической окружности
Чтобы пользоваться этим способом надо понимать как работает эта окружность. Постараюсь простым языком объяснить как это понимаю я. Думаю в школах на уроках алгебры эта тема объяснялась много раз умными словами учителя, в учебниках сложные формулировки. Лично я понимаю это как окружность, которую можно обходить бесконечное число раз, объясняется это тем, что функции синус и косинус периодичны.
Обойдем раз против часовой стрелки
Обойдем 2 раза против часовой стрелки
Обойдем 1 раз по часовой стрелки (значения будут отрицательные)
Вернемся к нашем вопросу, нам надо отобрать корни на промежутке [-7Pi/2; -2Pi]
Чтобы попасть к числам -7Pi/2 и -2Pi надо обойти окружность против часовой стрелки два раза. Для того, чтобы найти корни уравнения на этом промежутке надо прикидывать и подставлять.
Рассмотри x = Pi/2 + Pin. Какой приблизительно должен быть n, чтобы значение x было где-то в этом промежутке? Подставляем, допустим -2, получаем Pi/2 — 2Pi = -3Pi/2, очевидно это не входит в наш промежуток, значит берем меньше -3, Pi/2 — 3Pi = -5Pi/2, это подходит, попробуем еще -4, Pi/2 — 4Pi = -7Pi/2, также подходит.
Рассуждая аналогично для Pi/4 + 2Pin и -Pi/4 + 2Pin, находим еще один корень -9Pi/4.
Сравнение двух методов.
Первый способ (с помощью неравенств) гораздо надежнее и намного проще для пониманию, но если действительно серьезно разобраться с тригонометрической окружностью и со вторым методом отбора, то отбор корней будет гораздо быстрее, можно сэкономить около 15 минут на экзамене.
Видео:Урок 6 УРАВНЕНИЕ И ЕГО КОРНИ 7 КЛАСССкачать
Решение тригонометрических уравнений на промежутке
Разделы: Математика
Цель урока:
а) закрепить умения решать простейшие тригонометрические уравнения;
б) научить выбирать корни тригонометрических уравнений из заданного промежутка
Ход урока.
1. Актуализация знаний.
а)Проверка домашнего задания: классу дано опережающее домашнее задание – решить уравнение и найти способ выбора корней из данного промежутка.
1)cos x = -0,5, где хI [- 
]. Ответ: 
.
2) sin x = 
, где хI [0;2?]. Ответ: 
; .
3)cos 2x = —, где хI [0;
]. Ответ:
Ученики записывают решение на доске кто-то с помощью графика, кто-то методом подбора.
В это время класс работает устно.
Найдите значение выражения:
а) tg 
– sin 
+ cos 
+ sin . Ответ: 1.
б) 2arccos 0 + 3 arccos 1. Ответ: ?
в) arcsin 
+ arcsin 
. Ответ: 
.
г) 5 arctg (-
) – arccos (-). Ответ:– 
.
– Проверим домашнее задание, откройте свои тетради с домашними работами.
Некоторые из вас нашли решение методом подбора, а некоторые с помощью графика.
2. Вывод о способах решения данных заданий и постановка проблемы, т. е. сообщение темы и цели урока.
– а) С помощью подбора решать сложно, если задан большой промежуток.
– б) Графический способ не даёт точных результатов, требует проверку, и занимает много времени.
– Поэтому должен быть ещё как минимум один способ, наиболее универсальный -попробуем его найти. Итак, чем мы будем заниматься сегодня на уроке? (Учиться выбирать корни тригонометрического уравнения на заданном промежутке.)
– Пример 1. (Ученик выходит к доске)
cos x = -0,5, где хI [- ].
Вопрос: Отчего зависит ответ на данное задание? (От общего решения уравнения. Запишем решение в общем виде). Решение записывается на доске
х =
+ 2?k, где k 
R.
– Запишем это решение в виде совокупности:
– Как вы считаете, при какой записи решения удобно выбирать корни на промежутке? (из второй записи). Но это ведь опять способ подбора. Что нам необходимо знать, чтобы получить верный ответ? (Надо знать значения k).
(Составим математическую модель для нахождения k).
1 уровень: № 295 (а,б), № 317 (а,б)
2 уровень: № 307 (в), № 308 (б), № 326(б), № 327(б).
Видео:ЕГЭ по математике. Профильный уровень. Задание 5. Найдите корень уравненияСкачать
С1 (№15) с отбором корней на отрезке
В рамках подготовки к ЕГЭ по математике рассмотрим задачу С1 ( В новом формате ЕГЭ по математике – «Задание №13» ) , которая предлагалась в Тренировочной работе №60 А. Ларина.
а) Решите уравнение 
б) Найдите все корни на промежутке 
a)
Применяем формулу двойного угла для 
:
(1) или 
(2) ;
Уравнение (2) равносильно уравнению 
(произвели деление на 
).
Откладываем на оси синусов 
, на оси тангенсов 
. Выходим на четыре серии точек:
Ответ: 
б) Произведем отбор корней из отрезка 
при помощи тригонометрического круга:
Ответ: 
Чтобы не потерять страничку, вы можете сохранить ее у себя:
Можете подробно объяснить, как проводится отбор корней?
Следует хорошо ориентироваться в тригонометрическом круге.
Долго объяснять на словах…
Если никак с кругом, то
решаем сначала неравенство: 
Так как 
, то 
При 
, при 
.
Потом 
И так далее..
Помогите мне! Пn/2 на отрезке [0,1]
При n=0 x=0, 0 входит в [0;1].
При n=1 x=pi2, pi2>1.
Только 0.
Объясните по-подробнее какие страницы в какой последовательности надо читать, чтобы научиться отбирать корни тригонометрического уравнения в задании 13 профильного уровня!
А то я в приведённой вами ссылке в сообщении прочитал статью, на ней переход к странице: https://egemaximum.ru/trigonometricheskij-krug-ii/
А после этой страницы не написано куда дальше идти!
Спасибо большое!
Спасибо огромное вам!
Выручаете!=)
А подскажите, чтобы научиться правильно отбирать корни в 13ом задании нужно знать формулы приведения, суммы синусов и т. п?
И отличается ли отбор корней когда один оборот и когда несколько?!
Спасибо!
Для отбора корней не нужны формулы приведения, суммы синусов и т.п.
Принцип отбора – один, не важно полтора оборота, два или один…
Полезно хотя бы раз развернуть тригонометрический круг в ось. И увидеть, что, например, точки 
на круге отображаются одной точкой, а на оси – разными. Или, например, изобразите точки 
на круге, затем на оси…
Спасибо!
А при отборе корней с помощью окружности нужно что-то вычислять? Не понимаю когда находят серию корней как они определяют что будет корнем и отмечают это на окружности а что нет?
Не очень понятен вопрос…
Вам следует сперва научиться видеть серии корней на окружности. Только потом осваивайте отбор (при помощи тригонометрической окр.).
Например, если вас просят отметить на окружности точки 
а вы не понимаете, – как это. то до отбора далеко…
Начинайте перебирать различные значения 
смотрите, что получается…
Я про то, например, нашли серию корней: x=+_pi/6+pi n, n принадлежит Z.
Просят отобрать (в этапе б) корни на промежутке [2pi;3pi], я нахожу этот помежуток и выделяю его (это очень легко!).
А как вычислить корни, которые попадут на окружность на выделенный промежуток?!
Например, дано уравнение: 16cos^4x-24cos^2x+9=0
Его решить а.
Отобрать корни на промежутке [2pi; 3pi] б.
Нашел серию корней: x=+_pi/6+2pi n, n принадлежит Z.
Далее – черчу окружность, выделяю жирным промежуток, указанный в условии.
Мне не ясно, как туда попали корни 13 pi/6 и 17 pi/6.
Откуда они?
Спасибо огромное за объяснение!
Пока вы не выучите основные углы от нуля до 2пи на тригонометрическом круге, вы не сдвинетесь с места. Я вам много чего сказала по делу, но вы меня не слышите…
Я знаю эти углы! И как их отмечать на окружности! И формулы приведения!
Но я задал вопрос?
🔍 Видео
Отбор корней по окружностиСкачать
Задание №13. Как отбирать корни в тригонометрической окружности? 🤔Скачать
3,5 способа отбора корней в тригонометрии | ЕГЭ по математике | Эйджей из ВебиумаСкачать
Нахождение корней уравнения, принадлежащих промежуткуСкачать
Математика 5 класс. Уравнение. Корень уравненияСкачать
ЕГЭ база #7 / Логарифмические уравнения / Свойства, определение логарифма / решу егэСкачать
Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать
Три способа отбора корней в задании 13 ЕГЭ профильСкачать
🔴 Найдите корень уравнения 2+9x=4x+3 | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 7 | ШКОЛА ПИФАГОРАСкачать
Как разобраться в корнях ? Квадратный корень 8 класс | Математика TutorOnlineСкачать
АЛГЕБРА 7 класс : Уравнение и его корни | ВидеоурокСкачать
10 класс, 11 урок, Числовая окружностьСкачать
Какому из данных промежутков ... | ОГЭ 2017 | ЗАДАНИЕ 2 | ШКОЛА ПИФАГОРАСкачать
Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать
Свойства функции. Промежутки знакопостоянства. 10 класс.Скачать
Отбор корней по окружностиСкачать
7 задание из ОГЭ ( Ященко) Какому из данных промежутков принадлежит числоСкачать
🔴 Найдите корень уравнения (x-8)^2=(x-2)^2 | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 7 | ШКОЛА ПИФАГОРАСкачать
