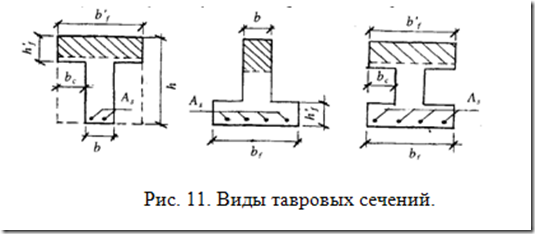
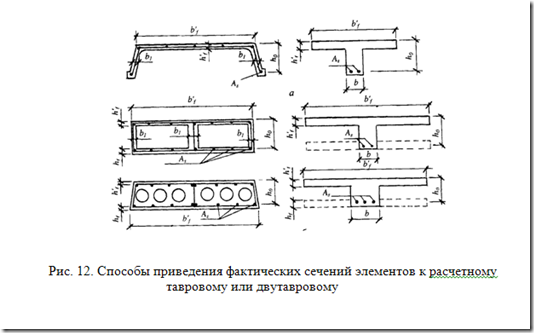
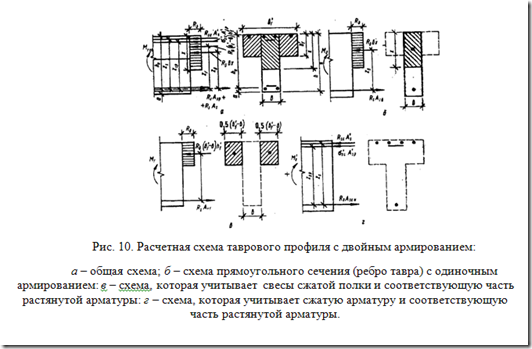
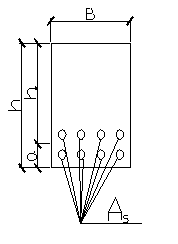
Изгибаемые железобетонные конструкции прямоугольного сечения не являются эффективными с точки зрения экономичности. Это связано с тем, что нормальные напряжения по высоте сечения при изгибе элемента распределяются неравномерно. В сравнении с прямоугольными сечениями тавровые сечения значительно выгоднее, т.к. при одной и той же несущей способности расход бетона в элементах таврового профиля меньше.
Тавровое сечение, как правило, имеет одиночное армирование.
В расчетах на прочность нормальных сечений изгибаемых элементов таврового профиля имеет место два расчетных случая.
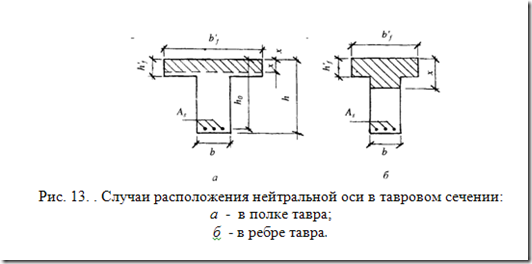
Алгоритм первого расчетного случая построен на предположении, что нейтральная ось изгибаемого элемента расположена в пределах сжатой полки.
Алгоритм второго расчетного случая построен на предположении, что нейтральная ось изгибаемого элемента расположена за пределами сжатой полки (проходит по ребру таврового сечения элемента).
Расчет прочности нормального сечения изгибаемого железобетонного элемента с одиночным армированием в случае, когда нейтральная ось расположена в пределах сжатой полки, идентичен алгоритму расчета прямоугольного сечения с одиночной арматурой шириной сечения равного ширине полки тавра.
Расчетная схема для этого случая представлена на рис 3.3.
Рис. 3.3. К расчету прочности нормального сечения изгибаемого железобетонного элемента в случае, когда нейтральная ось расположена в пределах сжатой полки.
Геометрически случай, когда нейтральная ось расположена в пределах сжатой полки означает, что высота сжатой зоны сечения тавра ( 
) не больше высоты сжатой полки 
и выражается условием: 
.
С точки зрения действующих усилий от внешней нагрузки и внутренних усилий это условие означает, что прочность сечения обеспечена, если расчетное значение изгибающего момента от внешней нагрузки (M) не превысит расчетного значения момента внутренних усилий относительно центра тяжести сечения растянутой арматуры при значениях 
.
M 
(3.25)
Если условие (3.25) выполняется, то нейтральная ось действительно расположена в пределах сжатой полки. В этом случае, необходимо уточнить какой размер ширины сжатой полки необходимо учитывать в расчете. Нормы 
устанавливают следующие правила:
Значение b ‘ f, вводимое в расчет; принимают из условия, что ширина свеса полки в каждую сторону от ребра должна быть не более 1 /6 пролета элемента и не более:
а) при наличии поперечных ребер или при h ‘ f ≥ 0,1h — 1 /2 расстояния в свету между продольными ребрами;
б) при отсутствии, поперечных ребер (или при расстояниях между ними больших, чем расстояния между продольными ребрами) и h ‘ f ‘ f
в) при консольных свесах полки:
Рассмотрим сечение сжатой зоны тавра как сумму, состоящую из двух прямоугольников (свесы полки) и прямоугольника относящегося к сжатой части ребра.
Условие прочности относительно центра тяжести растянутой арматуры.
M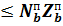 
+ 
(3.31)
где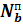 
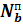
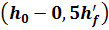
–усилие в сжатых свесах полки;
— плечо от центра тяжести растянутой арматуры до центра тяжести свесов полки;
–усилие в сжатой части ребра тавра;
—плечо от центра тяжести растянутой арматуры до центра тяжести сжатой части ребра.
= 
(3.32)
= 
(3.33)
= 
b 
(3.34)
= 
(3.35)
Подставим выражения (3.32 – 3.35) в формулу (3.31).
M 
+ b 
(3.36)
Преобразуем в выражении (3.36) второе слагаемое правой части уравнения аналогично преобразованиям выполненным выше (формулы 3.3; 3.4; 3.5)
Получим следующее выражение:
M + 
(3.37)
Отсюда определим численное значение 
.
= 
(3.38)
По значению из таблицы 
определим значения 
и𝛈.
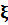
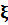
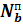
Сравним значение с граничным значением относительной высоты сжатой зоны 
. сечения элемента. Если выполняется условие 𝛏 
, то составляют условие равновесия проекций усилий на продольную ось элемента. ΣN=0
— — =0 (3.39)
= + b 
(3.40)
Отсюда определим необходимую площадь сечения растянутой продольной рабочей арматуры.
= 
(3.41)
По сортаменту стержневой арматуры 
необходимо подобрать значения площади растянутой продольной рабочей арматуры.
Видео:Определение усилий, напряжений и перемещений. СопроматСкачать
Особенности элементов таврового сечения.
Тавровое сечение встречаются в практике часто, как в отдельных железобетонных элементах — балках, так и в составе конструкций — в монолитных ребристых и сборных панельных перекрытиях. Тавровое сечение образуется из полки и ребра. В сравнении с прямоугольным экономичнее по расходу бетона элементы таврового сечения (несущая способность железобетонного элемента не зависит от площади сечения бетона растянутой зоны). Поэтому при одинаковой несущей способности расходуется меньше бетона за счет сокращения бетона растянутой зоны.
Элементы таврового сечения имеют, как правило, одиночное армирование.
При больших значениях ширины свесов удаленные от ребра участки свесов напряжены меньше, чем приближенные к ребру. Поэтому в расчетах ограничивают ширину свесов bf’ таврового сечения, учитываемую в расчете, заменяя ее на эквивалентную ширину свесов полки bf’ и полагая, что по всей площади сжатой зоны бетона действуют равные напряжения Rb. Она принимается с учетом таких значений свесов в каждую сторону от ребра:
— не более половины расстояния в свету между ребрами;
— не более 1/6 пролета рассчитываемого элемента;
-в элементах с полкой толщиной h’f ’ , поскольку форма сечения в растянутой зоне роли не играет (не учитывается в расчете).
Условие прочности имеет вид:
Дополнительное условие равновесия:
2 случай — нейтральная ось расположена в ребре; форма части сечения в сжатой зоне бетона — сложная (состоит из сжатых зон ребра и свесов полки). Поэтому при расчете разбивают эту зону на элементарные прямоугольники и соответствующие доли растянутой арматуры (так как усилие в сжатой зоне уравновешивается усилием в растянутой арматуре).
Условие прочности имеет вид:
Дополнительное условие равновесия:
Для тавровых сечений также должно быть соблюдено требование Норм: x£xR.
Определение расчетного случая положения в тавровом сечении при проверке прочности заданного сечения.
Так как известны все данные о сечении, включая площадь арматуры As, то приняв x=hf’ сравнить два усилия:
Если окажется Rs As £ Rb bf’ hf’, значит нейтральная ось проходит в полке тавра, т.е.
x £ hf’, и имеет место первый расчетный случай положения нейтральной оси в тавре. То есть для проверки прочности заданного сечения необходимо воспользоваться формулами (8) и (9).
Если окажется Rs As > Rb bf’ hf’, это означает, что x > hf’, имеет место второй случай положения нейтральной оси, и для проверки прочности заданного сечения следует воспользоваться формулами (10) и (11).
Определение расчетного случая положения нейтральной оси в тавровом сечении при подборе площади продольной арматуры.
При отсутствии данных о площади сечения арматуры As приняв x = hf’, определяют предельный внутренний момент Mf ’ который восприняло бы сечение при такой высоте сжатого бетона, записав его относительно центра тяжести неизвестной растянутой арматуры:
Если окажется, что М £ Mf ’ , граница сжатой зоны проходит в полке , т.е. имеет место первый расчетный случай положения нейтральной оси в тавре, и для подбора арматуры следует воспользоваться формулами (1) ¸(5) для прямоугольных сечений, заменяя в них b = bf ’ .
В противном случае имеет место второй случай положения нейтральной оси в тавре и для расчета арматуры следует применять формулы (10)-(11).
Дата добавления: 2017-05-18 ; просмотров: 3258 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Видео:Лекция по сопротивлению материалов № 1. Введение, внутренние силовые факторы, метод сечений.Скачать
Прямоугольные сечения изгибаемых элементов с одиночной арматурой, уравнения равновесия, условия прочности
h – высота нормального сечения
в – ширина ребра, ширина прямоугольного сечения
AS – площадь поперечного сечения растянутой арматуры
а – расстояние от центра тяжести растянутой арматуры до крайней растянутой фибры сечения, включая защитный слой бетона.
Защитный слой бетона зависит от размеров нормального сечения.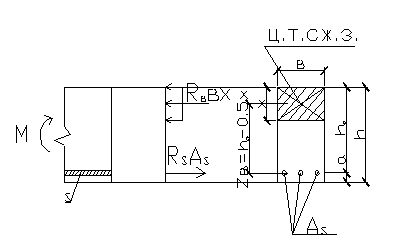 
Все расчетные формулы построены исходя из уравнения равновесия статики:
Расчетная схема сечения
zв –плечо внутренней пары сил
Из ур. равновесия
формируется условие прочности моментная точка в уровне центра тяжести арматуры.
Или моментная точка в уровне центра тяжести сжатой зоны.
Где высота сжатой зоны х определяется из уравнения равновесия ∑ N = 0
Два случая расчета тавровых сечений изгибаемых элементов, определения положения границы сжатой зоны
Тавровое сечение наиболее рациональное сечение изгибаемых элементов, так как есть возможность наибольшего отдаления сжатого бетона от растянутой арматуры. Идея оставления бетона только в сжатой зоне и для связи с группированной растянутой арматурой привела к формированию расчетных сечений, к снижению расхода бетона и арматуры.
Отсюда мы имеем два вида расчетных сечений двутавровое и тавровое.
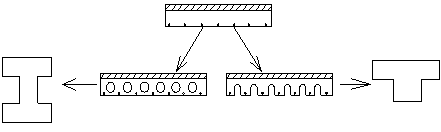
В 1 ƒ – ширина сжатой полки.
h 1 ƒ – высота сжатой полки.
Вƒ – ширина растянутой полки.
hƒ – высота растянутой полки.
При расчете прочности и то и другое сечение рассчитывается как тавровое без учета растянутых свесов.
Различают два расчетных случая
Граница сжатой зоны находится в полке.
Расчет проводится как для прямоугольного сечения шириной в = в 1 ƒ
Граница сжатой зоны находится в ребре
Расчет проводится как для таврового сечения с учетом сочетания прямоугольного сечения ребра глубиной В и высотой h и сжатых свесов с шириной (B — B 1 ƒ ) и высотой h 1 ƒ в сочетании.
Рассмотрим расчетную схему таврового сечения, а значит Х > h 1 ƒ и ζ ≤ ζR.
На основании расчетной схемы рассматриваем определение гр. сжатой зоны. Граница сжатой зоны проходит в ребре при выполнении двух условий.
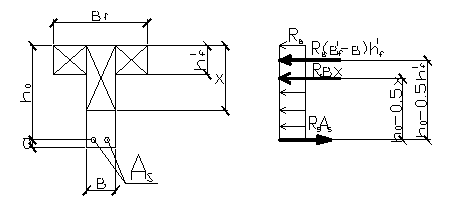
NS — усилие в растянутой арматуре
N 1 ƒ — усилие, воспринимаемое всей сжатой полке
Для выполнения равновесия ∑N = 0, граница сжатой зоны должна быть перемещена в ребро.
Данное условие используется для решения задач проверка прочности.
Второе условие: граница сжатой зоны находится в ребре если:
М – внешний расчетный момент
М 1 ƒ – условная несущая способность сечения, при полностью сжатой полке, т.е. при х = h 1 ƒ
Данное условие используется при решении задач подбор арматуры.
Вернемся к расчетной схеме.
Условие прочности формируется на основании уравнения равновесия ∑М = 0
М ≤ RB BХ (h0 – 0,5х) + RB (B 1 ƒ – В)h 1 ƒ *(h0 – 0,5h 1 ƒ ) (5) моментная точка в уровне центра тяжести растянутой арматуры.
Где Х определятся из уравнения равновесия ∑N = 0
🔥 Видео
Сопромат. Часть 1. Растяжение (сжатие). Построение эпюр продольных сил и нормальных напряжений.Скачать
Расчет изгибаемых ЖБ элементов с одиночным армированиемСкачать
Расчет значений Q и M для построения эпюр поперечных сил и изгибающих моментов балки на двух опорахСкачать
«ЖБ–Автоматизация–1». 5. Прочность наклонной полосы. (Reinforced concrete structure)Скачать
Расчет изгибаемых железобетонных элементов прямоугольного сечения с двойным армированием.Скачать
Задача о составной конструкцииСкачать
СОПРОМАТ. Плоский изгиб с распределённой нагрузкой. Задача 3.2. Часть 1.Скачать
Определение реакций опор в балке. Сопромат.Скачать
Сопротивление материалов. Лекция: косой изгиб и внецентренное растяжение-сжатиеСкачать
Проверка несущей способности изгибаемых жб элементов. Часть 1. Расчет неразрезного ригеля.Скачать
"ЖБ - Автоматизация - 1". 3. Трещиностойкость. Расчет. (Reinforced concrete structure)Скачать
Основы Сопромата. Расчеты на прочность. Общая идеяСкачать
Л 5 Карипбаева А Р ИзгибСкачать
Метод вырезания узлов. Определение усилий в ферме. СопроматСкачать
Общий расчет монолитных конструктивных систем с нелинейным процессором по СП 63.13330,СП 430.1325800Скачать
Пособие к СП 63: почему нельзя считать железобетонные конструкции по ЭВМ-программам Арбат и SCADСкачать
Сопротивление материалов. Лекция: дифференциальное уравнение изогнутой оси балкиСкачать
Сопротивление материалов. Занятие 15. Расчет стержня на косой изгиб.Скачать
