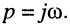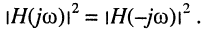Данная статья объясняет, что такое полюсы и нули, и обсуждает, как полюсы и нули передаточной функции связаны с поведением схем аналоговых фильтров относительно амплитуды и фазы.
В предыдущей статье я представил два стандартных способа представления передаточной функции в s-области для RC фильтра нижних частот первого порядка. Давайте кратко рассмотрим некоторые важные концепции.
- Передаточная функция математически выражает поведение фильтра в частотной области при передаче сигнала от входа к выходу.
- Мы можем написать передаточную функцию относительно переменной s , которая представляет собой комплексную частоту, и мы можем заменить s на jω , когда нам нужно вычислить амплитуду и сдвиг фазы на конкретной частоте.
- Нормированная форма передаточной функции похожа на шаблон, который помогает нам быстро определять определяющие характеристики фильтра.
- Математическое манипулирование нормированной передаточной функцией первого порядка позволяет нам продемонстрировать, что частота среза фильтра – это частота, на которой амплитуда уменьшается на 3 дБ, а фаза сдвигается на –45°.
- Полюсы и нули
- Влияние полюсов и нулей
- Влияние на фазу
- Скрытый ноль
- Заключение
- 2. Математическое описание систем автоматического управления ч. 2.9 — 2.13
- 2.9. Использование обратных преобразований Лапласа для решения уравнений динамики САР (звена)
- Пример
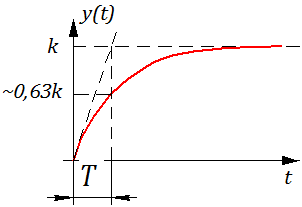
- 2.10. Весовая и переходная функции звена (системы).
- 2.11. Определение переходного процесса в системе (САР) (звене) через весовую и переходную функции. Формула Дюамеля-Карсона
- 2.12. Mетод переменных состояния.
- Пример решения задачи в форме коши.
- 2.13. Переход от описания переменных «вход-выход» к переменным состояния и обратно
- 2.13.1. Правая часть содержит только b0*u(t)
- 2.13.2. Правая часть общего вида
- Пример:
- Операторные передаточные функции
- Законы Ома и Кирхгофа в операторной форме
- Законы Кирхгофа в операторной форме
- Операторные сопротивления и проводимости элементов электрических цепей
- Для элемента активного сопротивления
- Для элемента индуктивности
- Для элемента ёмкости
- Операторные сопротивление и проводимость последовательного и параллельного двухполюсников
- Операторные сопротивление и проводимость двухполюсника общего вида
- Определение операторной передаточной функции. Связь с импульсной и переходной характеристиками
- Понятие о нулях и полюсах передаточной функции. Устойчивость передаточной функции
- Связь передаточной функции с частотными и временными характеристиками цепи
- 📺 Видео
Видео:[ТАУ]Записать передаточную функцию устройства [Составить диф. ур-е для условия передачи напряжения]Скачать
![[ТАУ]Записать передаточную функцию устройства [Составить диф. ур-е для условия передачи напряжения]](https://i.ytimg.com/vi/agDRxLaUWI4/0.jpg)
Полюсы и нули
Предположим, что у нас есть передаточная функция, в которой переменная s появляется как в числителе, так и в знаменателе. В этой ситуации, по крайней мере, одно значение s приведет к тому, что числитель будет равен нулю, и, по крайней мере, одно значение s приведет к тому, что знаменатель будет равен нулю. Значение, при котором числитель равен нулю, является нулем передаточной функции, а значение, которое приводит к нулю в знаменателе, является полюсом передаточной функции.
Давайте рассмотрим следующий пример:
В этой системе мы имеем ноль при s = 0 и полюс при s = –ω0 .
Полюсы и нули являются определяющими характеристиками фильтра. Если вы знаете расположение полюсов и нулей, то у вас много информации о том, как система будет реагировать на сигналы с разными входными частотами.
Видео:7) ТАУ для чайников.Части 3.4 и 3.5 : Передаточная функция. Преобразование Лапласа...Скачать

Влияние полюсов и нулей
Диаграмма Боде (логарифмическая амплитудно-частотная характеристика, АЧХ) обеспечивает простую визуализацию взаимосвязи между полюсом или нулем и поведением системы при передаче сигнала от входа к выходу.
Частота полюса соответствует угловой частоте, при которой наклон кривой АЧХ уменьшается на 20 дБ/декада, а ноль соответствует угловой частоте, при которой наклон увеличивается на 20 дБ/декада. В следующем примере амплитудно-частотная характеристика представляет собой аппроксимацию амплитудного отклика системы, которая имеет полюс при 10 2 радиана в секунду (рад/с) и ноль при 10 4 рад/с.

Видео:23) Построение Л.А.Ч.Х. и Л.Ф.Ч.Х. системы по её передаточной функцииСкачать

Влияние на фазу
В предыдущей статье мы видели, что математическим источником фазо-частотной характеристики фильтра нижних частот является функция арктангенса. Если мы используем функцию арктангенса (точнее, функцию отрицательного арктангенса), чтобы сгенерировать график зависимости фазы (в градусах) от частоты в логарифмическом масштабе, мы получим следующий график:
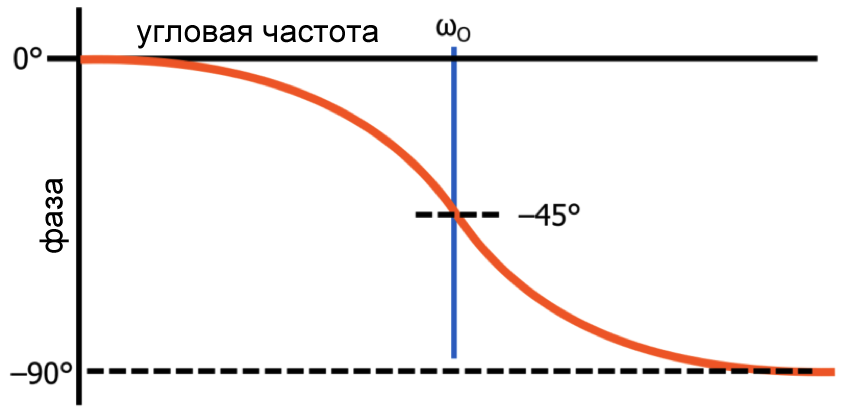
Аппроксимация логарифмической фазо-частотной характеристики для сдвига фазы, генерируемого полюсом, представляет собой прямую линию, представляющую сдвиг фазы -90°. Эта линия центрируется на частоте полюса и имеет наклон –45 градусов на декаду, что означает, что наклонная линия начинается за одну декаду до частоты полюса и заканчивается через одну декаду после частоты полюса. Влияние нуля будет таким же, за исключением того, что линия имеет положительный наклон, поэтому итоговый сдвиг фазы составляет +90°.
В следующем примере представлена система, которая имеет полюс при 10 2 рад/с и ноль при 10 5 рад/с.

Видео:Видеометодичка. Практикум по нахождению передаточных функций по дифференциальным уравнениямСкачать

Скрытый ноль
Если вы читали предыдущую статью, вы знаете, что передаточная функция фильтра нижних частот может быть записана следующим образом:
У этой системы есть ноль? Если мы применим определение, данное ранее в этой статье, мы сделаем вывод, что его нет – переменная s не появляется в числителе, и поэтому никакое значение s не приведет к тому, что числитель станет равным нулю.
Однако оказывается, что у нее на самом деле есть ноль, и чтобы понять почему, нам нужно рассмотреть более обобщенное определение полюсов и нулей передаточной функции: ноль ( z от «zero») возникает при значении s , которое заставляет передаточную функцию уменьшаться до нуля, а полюс ( p от «pole») возникает при значении s , которое заставляет передаточную функцию стремиться к бесконечности:
Имеет ли фильтр нижних частот первого порядка значение s , которое приводит к T(s) → 0 ? Да, это так, а именно, s = ∞ . Таким образом, система фильтра нижних частот первого порядка имеет полюс в точке ω0 и ноль в точке ω = ∞ .
Я попытаюсь дать физическую интерпретацию нуля при ω = ∞ : это указывает на то, что фильтр не может «всегда» продолжать увеличивать ослабление (где «всегда» относится к частоте, а не ко времени). Если вам удастся создать входной сигнал, частота которого продолжает увеличиваться до тех пор, пока она не «достигнет» бесконечности рад/с, то ноль при s = ∞ заставит фильтр прекратить увеличивать ослабление, т.е. наклон амплитудно-частотной характеристики увеличится с –20 дБ/декада до 0 дБ/декада.
Видео:Обратная функция. 10 класс.Скачать

Заключение
Мы изучили основные теоретические и практические аспекты полюсов и нулей передаточной функции и увидели, что можем создать прямую связь между частотами полюса и нуля фильтра и его амплитудно-частотной и фазо-частотной характеристиками. В следующей статье мы рассмотрим передаточную функцию фильтра верхних частот первого порядка.
Видео:Теория автоматического регулирования. Лекция 5. Модели параметров состоянийСкачать
2. Математическое описание систем автоматического управления ч. 2.9 — 2.13
Лекции по курсу «Управление Техническими Системами», читает Козлов Олег Степанович на кафедре «Ядерные реакторы и энергетические установки», факультета «Энергомашиностроения» МГТУ им. Н.Э. Баумана. За что ему огромная благодарность.
Данные лекции только готовятся к публикации в виде книги, а поскольку здесь есть специалисты по ТАУ, студенты и просто интересующиеся предметом, то любая критика приветствуется.
В предыдущих сериях:
В это части будут рассмотрены:
2.9. Использование обратных преобразований Лапласа для решения уравнений динамики САР (звена).
2.10. Весовая и переходная функции звена (системы).
2.11. Определение переходного процесса в системе (САР) (звене) через весовую и переходную функции.
2.12. Mетод переменных состояния.
2.13. Переход от описания переменных «вход-выход» к переменным состояния.
Попробуем применить, полученные знания на практике, создавая и сравнивая расчетные модели в разных видах. Будет интересно познавательно и жестко.
2.9. Использование обратных преобразований Лапласа для решения уравнений динамики САР (звена)
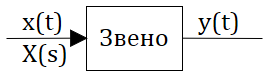
Рассмотрим динамическое звено САР изображенное на рисунке 2.9.1
Предположим, что уравнение динамики имеет вид:
где: — постоянные времени;
— коэффициент усиления.
Пусть известны отображения:
Найдем изображения для производных:
Подставим полученные выражения в уравнение динамики и получим уравнение динамики в изображениях:
B(s) — слагаемое, которое определяется начальными условиями, при нулевых начальных условиях B(s)=0.
W(s) — передаточная функция.
Передаточной функцией САР (звена) называется отношение изображений выходного сигнала к входному воздействию при нулевых н.у.
После того, как в явном виде найдено изображение для неизвестной выходной величины, нахождение оригинала не представляет сложностей. Либо по формуле Хэвисайда, либо разложением на элементарные дроби, либо по таблице из справочника.
Пример
Построить выходной сигнал звена САР при единичном входном воздействии и нулевых начальных условиях, если уравнение динамики звена имеет следующий вид:
входное воздействие: — единичное ступенчатое воздействие.
Выполним преобразование Лапласа:
Подставим в уравнение динамики и получим уравнение динамики в изображениях:
Для получения выходного сигнала из уравнения в изображениях выполним обратное преобразования Лапласа:
2.10. Весовая и переходная функции звена (системы).
Определение: Весовой функцией звена (системы) называется реакция системы при нулевых н.у. на единичное импульсное воздействие.
Определение: Переходной функцией звена (системы) при н.у. называется реакция на единичное ступенчатое воздействие.
На этом месте можно вспомнить, что преобразование Лапласа это интеграл от 0 до бесконечности по времени (см. предыдущий текст), а импульсное воздействие при таком интегрировании превращается в 1 тогда в изображениях получаем что:
Передаточная функция играет роль изображения реакции звена или системы на единичное импульсное воздействие.
Для единичного ступенчатого воздействия преобразование Лапласа тоже известно (см. предыдущий текст):
тогда в изображениях получаем, что реакция системы на ступенчатое воздействие, рассчитывается так:
Реакция системы на единичное ступенчатое воздействие рассчитывается обратным преобразованием Лапласа:
2.11. Определение переходного процесса в системе (САР) (звене) через весовую и переходную функции. Формула Дюамеля-Карсона
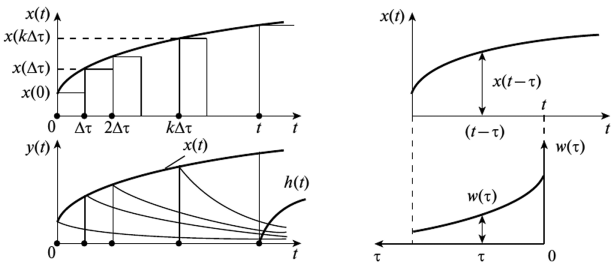
Предположим, что на вход системы поступает произвольное воздействие x(t), заранее известное. Найти реакцию системы y(t), если известны входное воздействие x(t) и весовая функция w(t).
Представим, что входное воздействие представляет собой последовательность прямоугольных импульсов до времени t и ступеньки высотой x(t) в момент времени t. см.рис. 2.11 Для каждого импульса мы можем записать реакцию системы через весовую функциию:
где:
— значение отклика по завершению предыущего импульса;
— время завершения текущего импульса;
— значение весовой функции в начале текущего импульса.
Тогда для определения занчения отклика в произвольный момент времени необходимо сложить все импульсы и ступенчатое воздействие в момент времени t:
Переходя к пределам
если перейти от t к бесконечности мы получим формулу интеграла Дюамеля-Карсона, или по другому «интеграла свертки» который обеспечивает вычисление оригинала функции по произвдению изображения двух функций:
где — вспомогательное время
Для вывода аналогичной зависмости от переходной функции вспомним что изображение весовой и переходной функции связаны соотношением: запишем выражение изображения для отклика в операторной форме:
Используя интеграл свертки получаем, что при известной переходной функции (h(t)) и известному входному воздействию х(t) выходное воздействие рассчитывается как:
2.12. Mетод переменных состояния.
До этого мы рассматривали системы с одной передаточной функцией, но жизнь всегда сложнее и как правило в системах есть несколько передаточных функций несколько входных воздейстий и несколько реакций системы. (см. рис. 2.12.1)
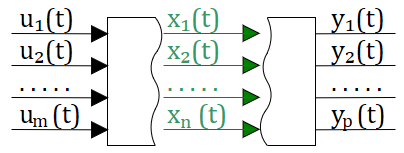
В этом случае наиболее удобной формой пердставления систем для их анализа и расчета оказался метод переменных состояния. Для этого метода, вместо передаточных функций связывающих вход с выходом используются дополнительные переменные состояния, которые описывают систему. В этом случае можно говорить, что состояние системы — это та минимальная информация о прошлом, которая необходима для полного описания будущего поведения (т.е. выходов) системы, если поведение ее входов известно. см. рис. 2.12.2
В методе состояний, производные всех переменных состояния, в общем случае зависит от всех переменных и всех входных воздействия, и могут быть записаны в представленной ниже системы обыкновенных дифференциальных уравнений (ОДУ) первой степени. Эта система уравнений называю системой ОДУ в форме Коши:
Выход из системы зависит от переменных состояния и, в общем случае от входных воздействий и описывается следующей системой уравнений:
где:
n — количество перемнных состояния,
m — количество входных воздействий,
p — количество выходных переменных;
Данная система уравнений может быть записана в матричной форме:
где:
— вектор входа (или вектор управления);
— вектор столбец производных переменных состояния;
— вектор столбец переменных состояния;
— вектор выхода;
— собственная матрица системы [n x n],
— постоянные коэффициенты;
— матрица входа [n x m],
— постоянные коэффициенты;
— матрица выхода а [p x n],
— постоянные коэффициенты;
— матрица обхода [p x m],
— постоянные коэффициенты;
В нашем случае почти всегда все элементы матрицы D будут нулевыми: D = 0.
Такое описание системы позволяет с одной стороны стандартным образом описывать различные технические системы. Явная формула для расчета производных позволяет достаточно просто осуществлять численное интегрирование по времени. И это используется в различных программах моделирования
Другое использование данного представления для простых систем, описанных в переменных «вход-выход», зачастую позволяет устранить технические трудности, связанные с решением ОДУ высокой степени.
Еще одним преимуществом данного описания, является то, что уравнения в форме Коши можно получить из законов физики
Пример решения задачи в форме коши.
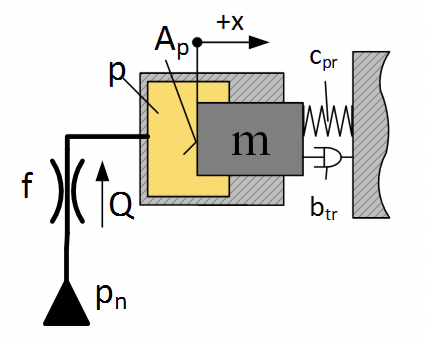
Рассмотрим задачу моделирования гидравлического привода, при следующих условиях:
Дано:
Цилиндрический плунжер диаметром 10 мм, с приведенной массой 100 кг, работает на пружину жесткостью 200 Н/мм и демпфер с коэффициентом вязкого трения — 1000 Н/(м/с). Полость начальным объемом 20 см 3 соединяется с источником давлния дросселем диаметром диаметр которого 0,2 мм. Коэффициент расхода дросселя 0.62. Плотность рабочей жидкости ρ = 850 кг/м 3 .
Определить:
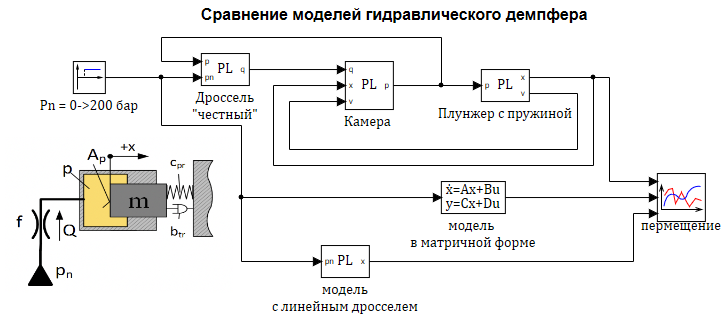
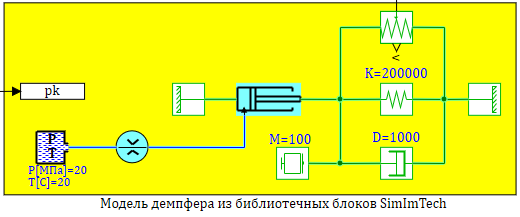
Перемещение дросселя, если в источнике давление происходит скачек 200 бар. см. рис. 2.12.13
Уравенение движение плунжера:
Где: – площадь плунжера,
– жесткость пружины,
– коэффициент вязкого трения, p – давление в камере.
Поскольку дифференциальное движения это уравнение второго порядка, превратим его в систему из двух уравнений первого порядка, добавив новую переменную — скорость , тогда
Уравнение давления в камере, для упрощения принимаем что изменениям объема камеры из-за перемещения плунжера можно пренебречь:
Где: Q – расход в камеру, V — объем камеры.
Расход через дроссель:
Где: f– площадь дросселя, – давление в источнике, p – давление в камере.
Уравнение дросселя не линейное, по условию задачи, давление входное изменяется скачком, от 0 до 200 бар, проведем линеаризацию в окрестности точки давления 100 бар тогда:
Подставляем линеаризованную формул расхода в формулу давления:
Таким образом общая система уравнений в форме Коши, для рис 2.12.3 привода принимает вид:
Матрицы A, B, С, В для матричной формы системы уравнений принимают вид:
Проверим моделированием в SimInTech составленную модель. На рисунке 2.12.13 представлена расчетная схема содержащая три модели:
1 — «Честная» модель со всеми уравнениями без упрощений.
2 — Модель в блоке «Переменные состояние» (в матричной форме).
3 — Модель в динамическом блоке с линеаризованным дросселем.
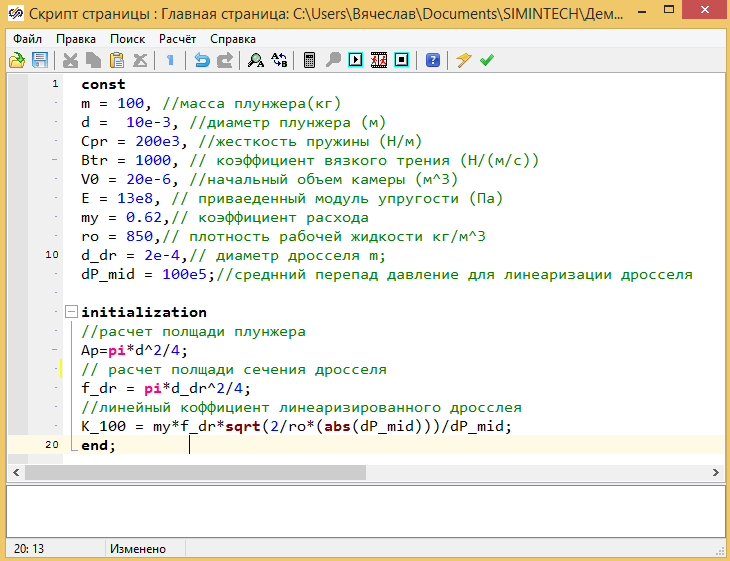
Все условия задачи задаются как глобальные константы проекта, в главном скрипте проекта, там же расчитываются на этапе инициализации расчета, площади плунжера и проходного сечения дросселя см. рис. 2.12.5:
Рисунок 2.12.5 Глобальный скрипт проекта.
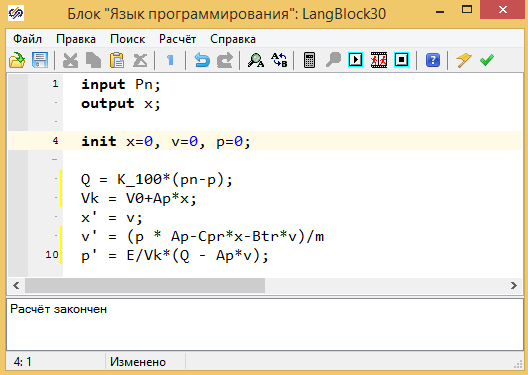
Модель на внутреннем языке программирования представлена на рис. 2.12.6. В данной модели используется описание модели в форме Коши. Так же выполняется учет изменения объема дросселя на каждом шаге расчета, за счет перемещения плунжера (Vk = V0+Ap*x.)
Рисунок 2.12.6 Скрипт расчета модели в форме Коши.
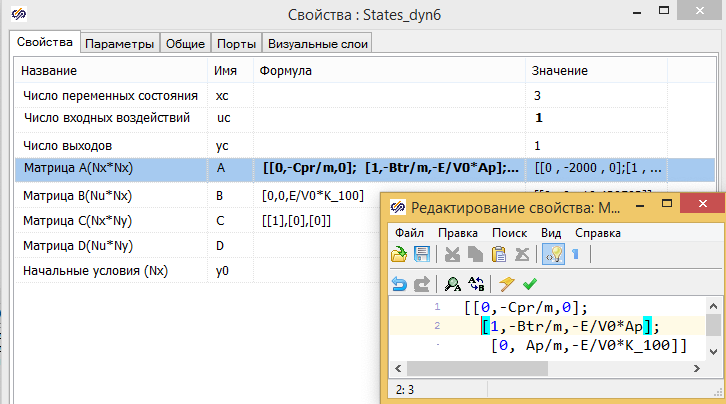
Модель в матричном форме задается с использованием глобальных констант в виде формул. (Матрица в SimInTech задается в виде последовательности из ее столбцов) см. рис. 2.12.7
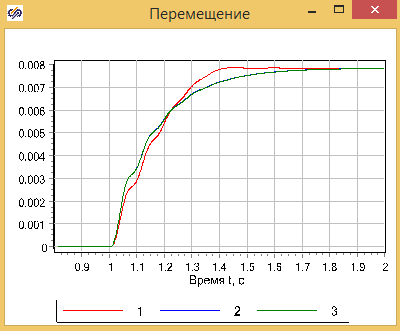
Результаты расчета показывают, что модель в матричной форме и модель на скриптовом языке в форме Коши, практически полностью совпадают, это означает, что учет изменения объема полости практически не влияют на результаты. Кривые 2 и З совпадают.
Процедура линеаризация расхода через дроссель вызывает заметное отличие в результатах. 1-й график c «честной» моделью дросселя, отличается от графиков 2 и 3. (см. рис. 2.12.8)
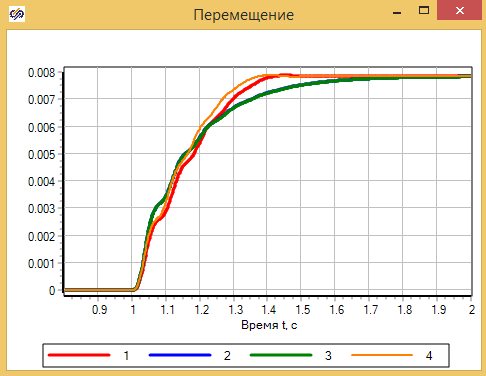
Сравним полученные модели, с моделью созданной из библиотечных блоков SimInTech, в которых учитываются так же изменение свойств реальной рабочей жидкости — масла АМГ-10. Сама модель представлена на рис. 2.12.9, набор графиков на рисунке 2.12.10
На графиках видно, что уточненная модель отличается от предыдущих, однако погрешность модели составлят наших упрощенных моделей составляют примерно 10%, в лишь в некоторые моменты времени.
2.13. Переход от описания переменных «вход-выход» к переменным состояния и обратно
Рассмотрим несколько вариантов перехода от описания «вход-выход», к переменным состояния:
Вариант прехода зависит от правой части уравнения с переменными «вход-выход»:
2.13.1. Правая часть содержит только b0*u(t)
В этом варианте, в уравнениях в правой части отсутствуют члены с производными входной величины u(t). Пример с плунжером выше так же относится к этому варианту.
Что бы продемонстрировать технологию перехода рассмотрим следующее уровнение:
Для перехода к форме Коши ведем новые переменные:
И перепишем уравнение относительно y»'(t):
Используя эти переменные можно перейти от дифференциального уравнения 3-го прядка, к системе из 3-х уравнений первого порядка в форме Коши:
Соотвественно матрицы для матричного вида уравнений в переменных сосотяния:
2.13.2. Правая часть общего вида
Более сложный случай, когда в уравнениях есть производные от входных воздействий и уравнение в общем случае выглядит так:
Сделаем преобразования: перейдем к уравнениям динамики в изображениях:
Тогда можно представить уравнение в изображениях в виде:
Разделим уравнение в изображениях на произведение полиномов , получим:
Где: — некоторая комплексная величина (отношение двух комплексных величин). Можно считать, что
отображение величины
. Тогда входная величина может быть в изображениях представлена как:
Вренемся к оригиналу от изображений получим: ,
где: — дифференциальный оператор.
А это дифференциальное уравнение n-го порядка мы можем преобразовать к системе из n дифференциальных уравнений первого порядка, как это мы делали выше:
Таким образом, мы получили систему уравнение в форе Коши, относительно переменных состояния :
А регулируемую величину (выход системы) мы так же можем выразить через эти переменные, в изображениях:
Перейдем от изображения к оригиналам:
Если обозначить вектор , то мы получим уравнения переменных состояниях в матричной форме, где D = 0:
Пример:
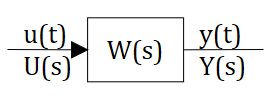
Рисунок 2.13.1 Передаточная функция.
Имеется передаточная функция (рис. 2.13.1) в изображениях :
Необходимо преобразовать передаточную функцию к системе уравнений в форме Коши
В изображения реакция системы связана с входным воздействие соотношением:
Разделим в последнем правую и левую часть на произведения , и введем новую перменную
:
Полиномы N(s) и L(s) равны:
Перейдем в последнем выражении от изображения к оригиналам и ведем новые переменные (состояния):
Переходим от уравнения третьего порядка к системе трех уравнений первого порядка:
Или в матричной форме:
Для получения второго матричного уравнения воспользуемся соотношением для новых переменных в отображениях:
Перейдем от изображений к оригиналу:
Таким образом второе уравнение матричной системы выглядит так:
Проверим в SimInTech сравнив передаточную функцию и блок переменных состояния, и убедимся, что графики совпадают см. рис. 2.13.2
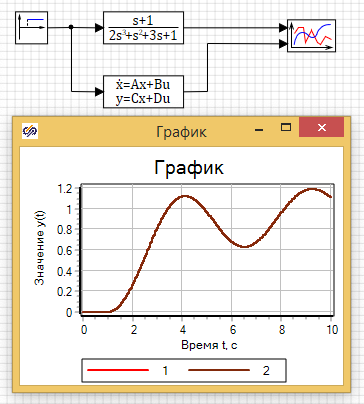
Рисунок 2.13.2 Сравнение переходного процеса у блока передаточной функции и блока переменных состояния.
Видео:Техническая механика/ Определение равнодействующей. Плоская система сходящихся сил.Скачать

Операторные передаточные функции
Содержание:
Операторные передаточные функции:
Практический смысл и назначение операторного метода в теории электрических цепей состоит, прежде всего, в представлении соотношения вход/выход в операторной форме, что даёт возможность существенно упростить процедуры анализа и синтеза электрических цепей и обеспечить связь между временным и частотным описаниями как колебаний, действующих в цепи, так и самой цепи.
Видео:Теория автоматического управления. Лекция 8. Дискретные САУ. Аналог критерия устойчивости МихайловаСкачать

Законы Ома и Кирхгофа в операторной форме
Покажем, что решение задач анализа колебаний в электрической цепи существенно упрощается при использовании операторного метода.
Законы Кирхгофа в операторной форме
Пусть токи
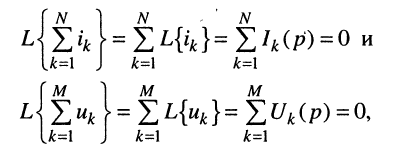
что говорит о формальной справедливости законов Кирхгофа для токов и напряжений, выраженных в операторной форме.
Операторные сопротивления и проводимости элементов электрических цепей
Убедимся в справедливости закона Ома для L-изображений колебаний на зажимах элементов R, L, С при нулевых начальных условиях (см.разд. 15.2) и найдём операторные изображения 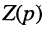
Для элемента активного сопротивления
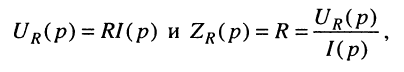
т. е. операторное активное сопротивление равно самому активному сопротивлению, поэтому операторная активная проводимость равна самой активной проводимости
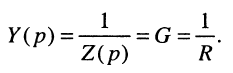
Для элемента индуктивности
правило дифференцирования даёт:
откуда операторные сопротивление и проводимость индуктивности равны:
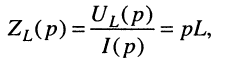
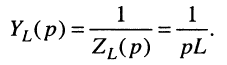
Для элемента ёмкости
правило интегрирования даёт:
откуда операторные сопротивление и проводимость ёмкости равны:
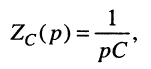
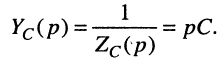
Заметим, что поскольку оператор р согласно (16.2) определён как комплексное переменное
операторные сопротивления и проводимости элементов L и С получаются заменой оператора 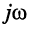
Операторные сопротивление и проводимость последовательного и параллельного двухполюсников
Закон Ома при нулевых начальных условиях формально верен и для сложных двухполюсников, если в числе их элементов не содержатся независимые источники.
Определение:
Операторным сопротивлением 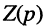
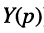
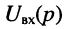
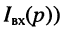
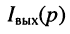
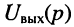
(соответственно 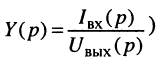
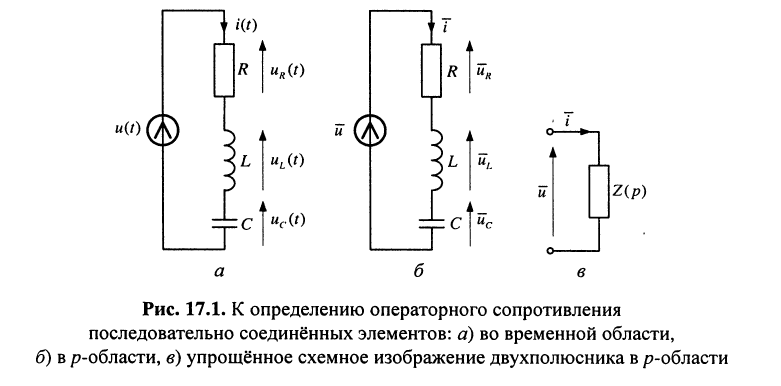
Найти операторное сопротивление двухполюсника (рис. 17.1), состоящего из последовательно соединённых элементов R, L, С при нулевых начальных условиях.
Решение. Напряжение на зажимах двухполюсника при нулевых начальных условиях равно
Применим к полученному уравнению преобразование Лапласа:
откуда следует, что при последовательном соединении элементов их операторные сопротивления складываются, как и для комплексных сопротивлений, но оператор 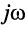
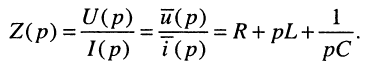
Пример 17.2.
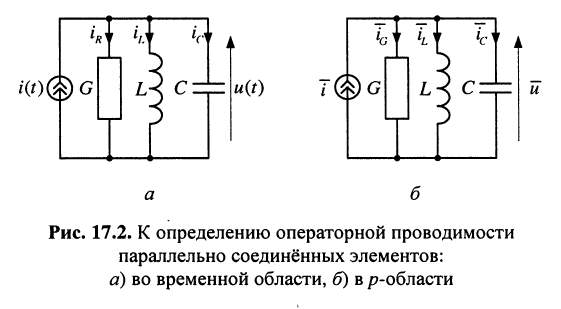
Найти операторную проводимость двухполюсника (рис. 17.2), состоящего из параллельно соединённых элементов R, L, С при нулевых начальных условиях.
Решение. Для тока 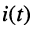
поэтому операторную проводимость заданного двухполюсника можно записать сразу:
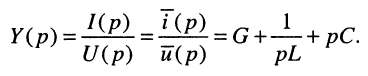
В силу дуальности последовательного и параллельного контуров выражение (17.9) можно было записать сразу на основании формулы (17.8).
Выражения (17.8) и (17.9) представляют собой входные операторные функции цепи. Они дают основания определению операторного сопротивления и проводимости двухполюсника общего вида.
Операторные сопротивление и проводимость двухполюсника общего вида
Закон Ома, при нулевых начальных условиях, формально можно применить и для сколь угодно сложных двухполюсников. Ранее
(см. лекцию 5) было установлено, что если на входе двухполюсника действует источник напряжения с ЭДС 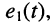
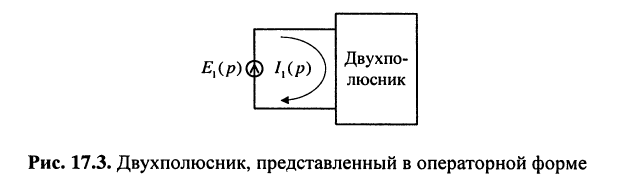
Переходя к L-изображениям напряжений, токов и сопротивлений элементов цепи, получим представление двухполюсника в операторной форме (рис. 17.3), что позволяет записать L-изображение входного тока:
Теперь согласно определению операторной проводимости и операторного сопротивления имеем:
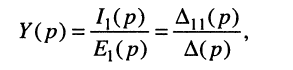
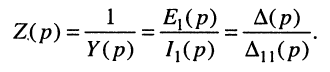
При этом нужно помнить, что определители и алгебраические дополнения в таких формулах записываются с учётом свойств преобразования Лапласа, как это сделано в примерах 17.1 и 17.2.
Определение операторной передаточной функции. Связь с импульсной и переходной характеристиками
В лекции 15 было показано, что во временной области соотношение вход/выход линейной электрической цепи при произвольном воздействии описывается уравнением свёртки:
где h(t) — импульсная характеристика, x(t) — воздействие, y(t) — реакция. При этом воздействие и реакция могут быть напряжениями или токами.
Для описания соотношения вход/выход в операторной форме воспользуемся L-изображением свёртки
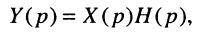
откуда получаем соотношения вход/выход в операторной форме
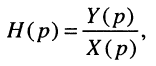
которое называют передаточной функцией.
Определение:
Передаточной функцией линейной электрической цепи называется отношение L-изображения реакции к L-изображению воздействия при нулевых начальных условиях.
Выражение (17.13) говорит о том, что передаточная функция является L-изображением импульсной характеристики, т. е. импульсная характеристика является обратным преобразованием Лапласа передаточной функции:
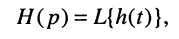
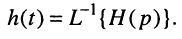
Именно этими зависимостями объясняется содержащееся в определении передаточной функции требование нулевых начальных условий.
Связь между передаточной функцией и переходной характеристикой можно установить, если воспользоваться интегралом Дюамеля (15.20а) при нулевых начальных условиях:
когда 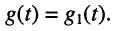
Первый сомножитель правой части полученного уравнения содержит L-изображение производной, поэтому окончательно можно записать:
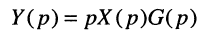
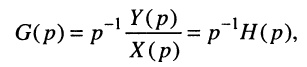
что полностью соответствует связи импульсной и переходной характеристик (15.16).
Обратим внимание на то, что передаточная функция может быть получена из комплексных частотных характеристик формальным образом, а именно — простой заменой в КЧХ 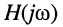
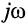
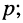
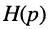
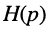
В зависимости от того, какая величина выступает в качестве внешнего воздействия, а какая в качестве реакции цепи, различают четыре вида передаточных функций:
операторное передаточное сопротивление
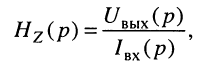
операторную передаточную проводимость
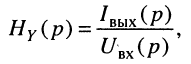
передаточную функцию по току
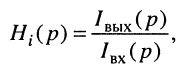
передаточную функцию по напряжению
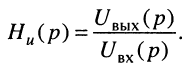
Последние две функции иногда называют операторными передаточными коэффициентами по току и по напряжению соответственно.
По любой из передаточных функций (17.18)—(17.21) нетрудно найти L-изображение реакции цепи, а затем и саму реакцию на заданное воздействие, поскольку любая передаточная функция Н(р) согласно (17.12) может рассматриваться как связующий коэффициент между L-изображения ми воздействия Х(р) и реакции Y(p).
Пример 17.3.
Записать передаточную функцию для последовательного колебательного контура (рис. 17.1, б) относительно напряжения на индуктивности.
Решение. По определению передаточной функции для индуктивности имеем
Но операторное напряжение на индуктивности равно:
Подставляя сюда операторное сопротивление (17.8), получаем искомую передаточную функцию:
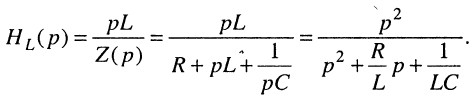
Аналогично можно получить и другие передаточные функции для последовательной, параллельной или более сложной цепи. В последнем случае потребуется составить систему уравнений для L-изображений колебаний, воспользовавшись методом контурных токов или узловых напряжений.
Понятие о нулях и полюсах передаточной функции. Устойчивость передаточной функции
Задача 17.1.
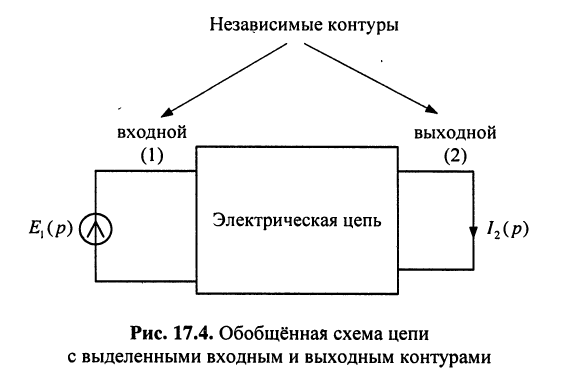
Получить и исследовать общее выражение для передаточной функции цепи, когда воздействие представляет собой ЭДС источника напряжения, а реакцией является ток в выделенной ветви анализируемой цепи (рис. 17.4).
Решение. Выберем независимые контуры в цепи так, чтобы через источник напряжения замыкался ток только одного входного контура, а через интересующую нас ветвь — ток только одного выходного контура. На рис. 17.4 они обозначены индексами 1 и 2 соответственно.
Теперь, как и в задаче 5.2, необходимо положить 
откуда по определению передаточной функции имеем операторную передаточную проводимость
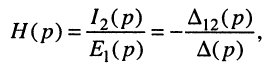
где 
a 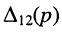
Заметим, что определитель и все его миноры представляют собой рациональные функции оператора р, все коэффициенты которых являются вещественными числами. Это объясняется тем, что при раскрытии определителя над его элементами совершаются только операции умножения, сложения и вычитания, а сами элементы представляют собой простейшие рациональные
функции с вещественными коэффициентами вида (17.11). Раскрывая определитель 
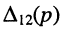
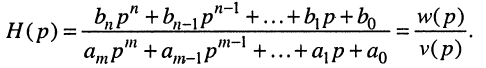
Полиномы числителя 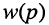
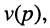
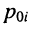
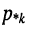
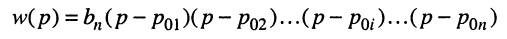
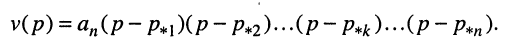
Отсюда передаточная функция (17.24) приобретает вид:
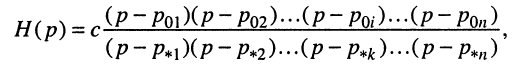
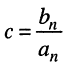
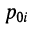
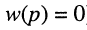
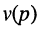
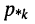
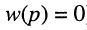
Названия корней уравнения 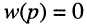
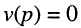
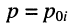
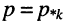
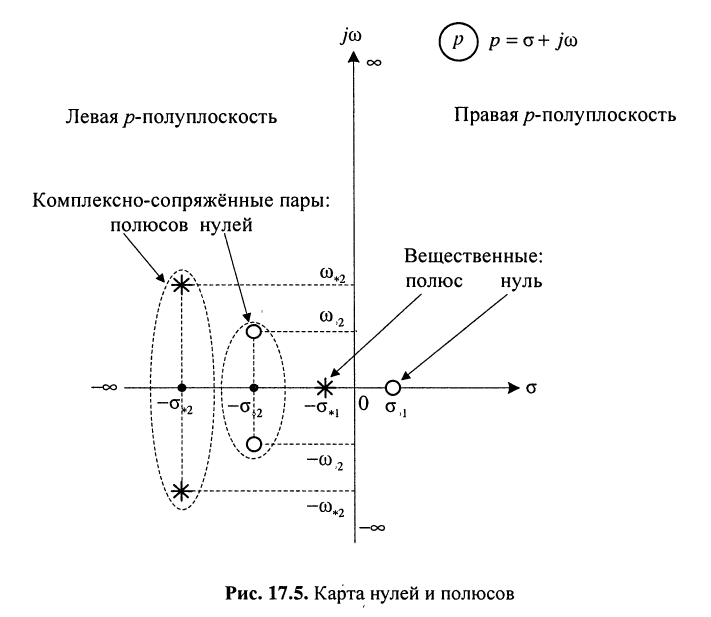
Нули и полюсы наглядно отображаются на комплексной p -плоскости (рис. 17.5) значками ( ° ) и ( * ) соответственно.
На рис. 17.5 показаны:
- вещественный положительный нуль
и отрицательный полюс
у которых частота
- пара комплексно-сопряжённых нулей
и
и пара комплексно-сопряжённых полюсов
и 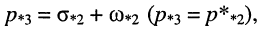
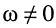
Отображение нулей и полюсов на p-плоскости называют картой нулей и полюсов. Различают левую и правую р-полуплоскости.
Карта нулей и полюсов позволяет оценить ряд свойств электрической цепи и, в частности, определить её устойчивость с точки зрения устойчивости передаточной функции.
Утверждение:
цепь является строго устойчивой тогда и только тогда, когда её передаточная функция имеет, полюсы только в левой р-полуплоскости, исключая мнимую ось.
Доказательство. Напомним, что цепь называется строго устойчивой, если при нулевых начальных условиях ограниченное по величине воздействие
вызывает ограниченную по величине реакцию
Но реакцию y(t) при нулевых условиях можно найти с помощью уравнения свёртки
Отсюда при заданных ограничениях имеем соотношение
из которого следует, что для получения равномерно ограниченной для всех t реакции, т. е. для обеспечения строгой устойчивости цепи должно выполняться условие абсолютной сходимости интеграла от импульсной характеристики:
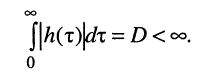
Найдём расположение полюсов, которое соответствует полученному условию. Для этого представим импульсную характеристику h(t) цепи как обратное L-изображение передаточной функции (17.15) путём разложения последней на сумму простых дробей (16.28):
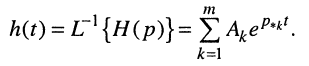
Подставим в интеграл (17.28) правую сумму (17.29)
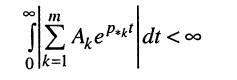
и проведём ряд несложных преобразований.
Поскольку модуль суммы не превосходит суммы модулей, справедливо следующее неравенство:
В правой части полученного неравенства поменяем местами знаки суммирования и интегрирования и оставим только знак равенства:
Рассмотрим интеграл в правой части равенства, содержащий модуль экспоненты, при
во-вторых, первая экспонента под интегралом всегда неотрицательна, поэтому знак модуля можно опустить:
Остаётся исследовать сходимость интеграла при положительном и отрицательном показателе
Сходимость интеграла при 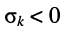
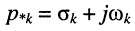
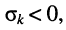
Связь передаточной функции с частотными и временными характеристиками цепи
Как было показано в лекции 10, для определения частотных характеристик АЧХ 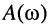
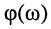
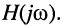
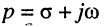
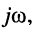
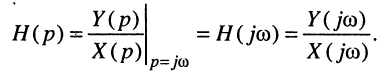
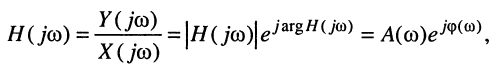
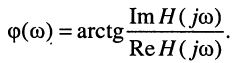
Эквивалентное выражение для КЧХ получается из (17.31), если воспользоваться комплексными функциями числителя и знаменателя:
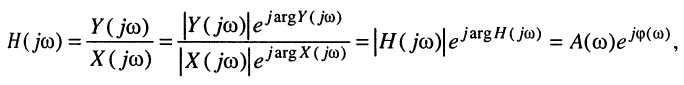
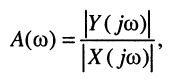
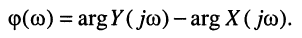
Вследствие того, что функция
является иррациональной, обычно при анализе и синтезе цепей используют квадрат АЧХ:
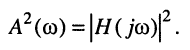
Перечислим основные свойства передаточных функций и квадрата АЧХ пассивных цепей.
- Передаточная функция является L-изображением импульсной характеристики.
- Передаточная функция является дробно-рациональной функцией с вещественными коэффициентами.
- Полюсы устойчивой передаточной функции лежат в левой р-полуплоскости.
- Степени полиномов числителей передаточной функции и квадрата АЧХ не превышают степеней полиномов знаменателей; приневыполнении этого свойства АЧХ на бесконечно больших частотах
должна принимать бесконечно большое значение, поскольку числитель в этом случае растёт быстрее знаменателя.
- Частотные характеристики цепи вычисляются по передаточной функции при подстановке
- Квадрат АЧХ является чётной рациональной функцией переменной с вещественными коэффициентами:
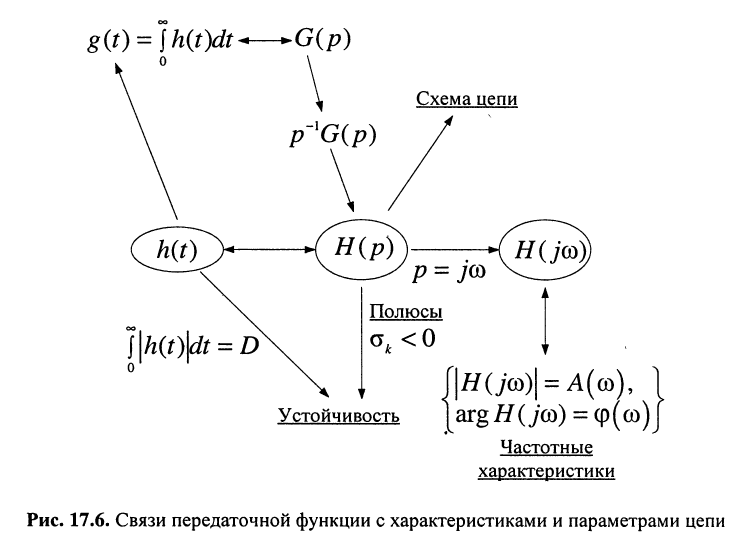
- По передаточной функции можно изобразить схему цепи
Обобщённая схема связи передаточной функции с характеристиками и свойствами цепи представлена на рис. 17.6.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Свободные колебания в пассивных электрических цепях
- Цепи с распределёнными параметрами
- Волновые параметры длинной линии
- Колебания в линиях без потерь
- Комплексные функции электрических цепей
- Гармонические колебания в колебательном контуре
- Частотные характеристики линейных электрических цепей
- Частотные методы анализа и расчёта электрических цепей
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
📺 Видео
Передаточные функцииСкачать

Линейные системы автоматического регулирования. Лекция 1. Классификация САУСкачать

16) ТАУ для чайников. Часть 4.8. ЛАФЧХ сложных звеньевСкачать

10 класс, 10 урок, Обратная функцияСкачать

Линейная функция, квадратичная функция и обратно-пропорциональная функция | Математика | TutorOnlineСкачать

Промежутки знакопостоянства функции.Скачать
14.1. Касательная к параметрически заданной функцииСкачать

Предельные вероятности состоянийСкачать

Преобразование структурных схем систем управленияСкачать

proТАУ: 1. Передаточная функцияСкачать

6. Особые решения ДУ первого порядкаСкачать

proТАУ: 4. Разомкнутая и замкнутая системы управленияСкачать


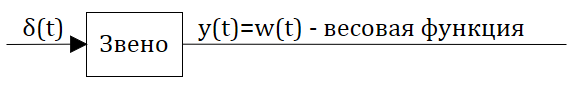
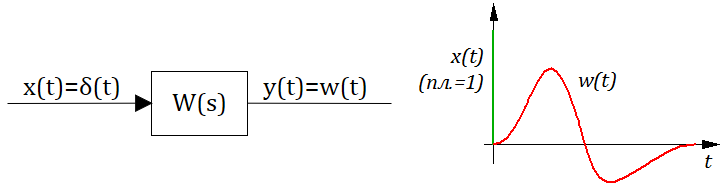
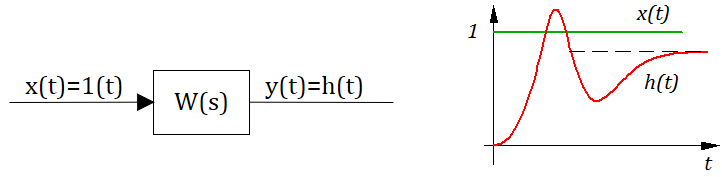
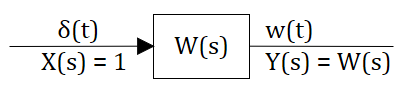
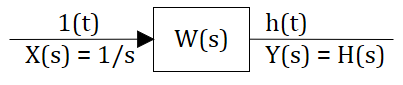
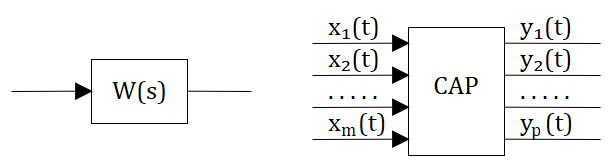
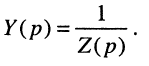
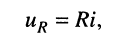
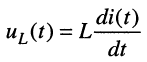
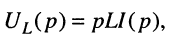
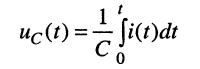
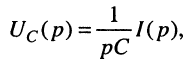
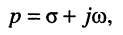
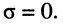
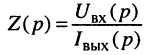
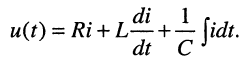
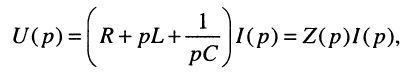
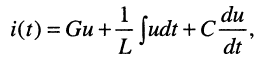
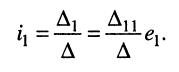
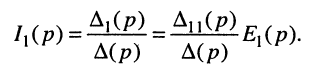
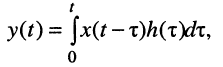
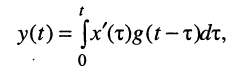
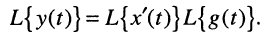
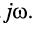
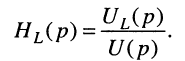
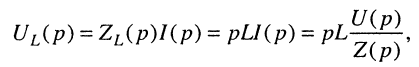
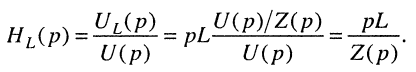
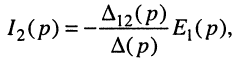
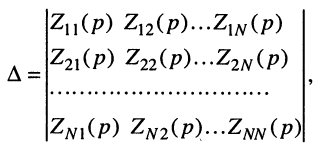
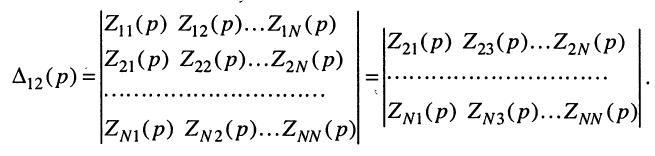
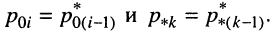
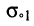 и отрицательный полюс
и отрицательный полюс 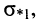 у которых частота
у которых частота 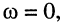
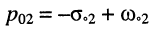 и
и 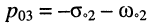
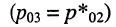 и пара комплексно-сопряжённых полюсов
и пара комплексно-сопряжённых полюсов 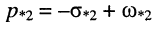
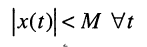
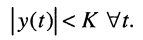
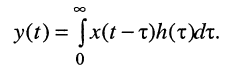
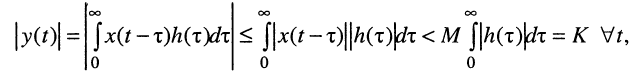
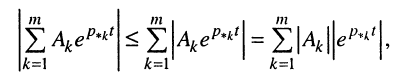
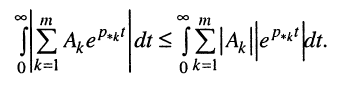
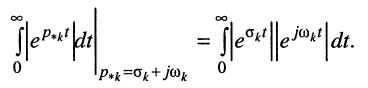
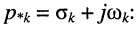
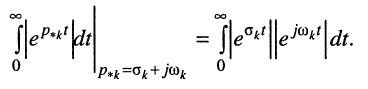
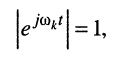
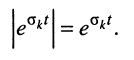
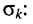
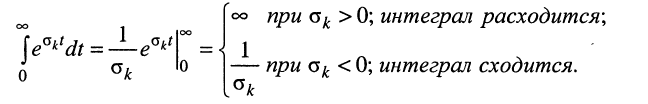
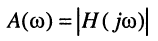
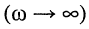 должна принимать бесконечно большое значение, поскольку числитель в этом случае растёт быстрее знаменателя.
должна принимать бесконечно большое значение, поскольку числитель в этом случае растёт быстрее знаменателя.