Исследовательская работа по решению иррациональных уравнений (7 видео)

Проект по алгебре «Иррациональные уравнения»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Муниципальное бютжетное общеобразовательное

учреждение Зайцевская основная школа

Ярцевского района Смоленской области

Проект по учебному курсу «Избранные вопросы математики»

Выполнила: ученица 8 класса Элисова Елизавета

Руководитель : Матюхова О.А.

В школьном курсе алгебры рассматриваются различные виды уравнений – линейные, квадратные, биквадратные, кубические, рациональные, иррациональные и другие. Данная работа посвящена иррациональным уравнениям, методам их решения.

С иррациональными уравнениями мы знакомимся в 8 классе на нескольких уроках, для более подробного знакомства с иррациональными уравнениями этого времени мало, поэтому я решила более детально познакомиться с такими уравнениями и методами их решения.

Цель исследования — обобщить и систематизировать информацию о приёмах решения иррациональных уравнений.

Предмет исследования — иррациональные уравнения, включенные в школьный учебник 8 класса, сборники задач.

Гипотеза исследования умение решать иррациональные уравнения.

Цель, предмет и гипотеза исследования обусловили выдвижение и решение следующих задач исследования:

1.Изучить литературу по данной теме.

2.Провести исследование и анализ имеющихся способов решения.

3.Выбрать из найденных способов решения наиболее оптимальные.

4.Провести обобщение и систематизацию имеющего материала.

Изучение различной литературы на данную тему.

Анализ теоретических источников.

Систематизация знаний по решению уравнений.

Обобщение материалов в литературе.

История иррационального числа

Термин “рациональное” (число) происходит от латиноамериканского слова ratio – отношение, которое является переводом греческого слова “логос”в отличие от рациональных чисел, числа, выражающие отношение несоизмеримых величин, были названы еще в древности иррациональными, т.е. нерациональными (по-гречески “алогос”) правда, первоначально термины “рациональный” и “иррациональный” относились не к числам, а к соизмеримым и соответственно не соизмеримым величинам, которые пифагорейцы называли выразимыми и невыразимыми, Теодор Киренский же симметричными и ассимметричными. В V-VI вв. римские авторы Капелла и Кассиодор переводили эти термины на латынь словами rationalis и irrationalis. Термин “соизмеримый” (commensurabilis) ввел в первой половине VI в. другой римский автор- Боэций.

Древнегреческие математики классической эпохи пользовались только рациональными числами (вернее целыми, дробными и положительными). В своих “Началах” Евклид излагает учение об иррациональностях чисто геометрически.

Математики Индии, Ближнего и Среднего Востока, развивая алгебру, тригонометрию и астрономию, не могли обойтись без иррациональных величин, которые, однако, длительное время не признавали за числа. Греки называли иррациональную величину, например, корень из квадратного числа, “алогос” – невыразимое словами, а позже европейские переводчики с арабского на латынь перевели это слово латинским словом surdus – глухой. В Европе термин surdus- глухой впервые появился в середине XII в. у Герарда Кремонского, известного переводчика математических прозведений с арабского на латынь, затем у итальянского математика Леонардо Фабоначчи и других европейских математиков, вплоть до XVIII в. Правда уже в XVI в. Отдельные ученые,

в первую очередь итальянский математик Рафаэль Бомбелли и нидерландский математик Симон Стевин считали понятие иррационального числа равноправным с понятием рационального числа. Стевин писал: “Мы приходим к выводу, что не существует никаких абсурдных, иррациональных, неправильных, необъяснимых или глухих чисел, но что среди чисел существует такое совершенство и согласие, что нам надо размышлять дни и ночи над их удивительной закономерностью.”

Еще до Бомбелли и Стевина многие ученые стран Среднего Востока в своих трудах употребляли иррациональные числа как полноправные объекты алгебры. Более того, комментируя “Начала” Евклида и исследуя общую теорию отношения Евдокса, Омар Хайям уже в начале XII в. теоретически расширяет понятие числа до положительного действительного числа. В том же направлении много было сделано крупнейшим математиком XIII в. ат-Туси.

Математики и астрономы Ближнего и Среднего Востока вслед за астрономами древнего Вавилона и эллинистической эпохи широко пользовались шестидесятеричными дробями, арифметические действия с которыми они называли “арифметикой астрономов”. По аналогии с шестидесятеричными дробями самаркандский ученый XV в. ал-Каши в работе “Ключ арифметики” ввел десятичные дроби которыми он пользовался для повышения точности извлечения корней. Независимо от него по такому же пути шел открывший в 1585 г. десятичные дроби в Европе Симон Стевин, который в своих “приложениях к алгебре” (1594 г.) показал, что десятичные дроби можно использовать для бесконечно близкого приближения к действительному числу. Таким образом, уже в XVI в. зародилась идея о том, что естественным аппаратом для введения и обоснования понятия иррационального числа являются десятичные дроби. Появление “Геометрии” Декарта облегчило понимание связи между измерением любых отрезков (и геометрических величин вообще) и необходимости расширения понятия рационального числа. На числовой оси иррациональные числа, как и рациональные, изображаются точками. Это геометрическое толкование позволило лучше понять природу иррациональных чисел и способствовало их признанию.

В современных учебных руководствах основа определения иррационального числа опирается на идеи ал-Каши, Стевина и Декарта об измерении отрезков и о неограниченном приближении к искомому числу с помощью бесконечных десятичных дробей. Однако обоснованием свойств действительных чисел и полная теория их была разработана лишь в XIX в.

Методы решения уравнений:

1.Возведение обеих частей уравнения в степень.

2. Использование равносильных переходов.

3. Умножение левой части на сопряженное выражение.

4. Введение новой переменной.

Познакомимся с каждым из методов.

Возведение обеих частей уравнения в степень.

А = В + Проверка корней

(т.к. могут появиться лишние корни)

При возведении в четную степень возможно расширение области определения заданного уравнения. Поэтому при решении таких иррациональных уравнений обязательна проверка.

При возведении в нечетную степень обеих частей иррационального уравнения область определения не меняется.

При решении иррациональных уравнений необходимо учитывать следующее:

1) если показатель корня — четное число, то подкоренное выражение должно быть неотрицательно; при этом значение корня также является неотрицательным (определение корня с четным показателем степени);

2) если показатель корня — нечетное число, то подкоренное выражение может быть любым действительным числом; в этом случае знак корня совпадает со знаком подкоренного выражения.

Примеры решения уравнений:

1. = х – 2

2х – 1 = ( х – 2 )

2х – 1 = х — 4х + 4

х— 6х +5 = 0

Д = в— 4 ас = 36 – 4 ∙1∙5 = 16

х = = 5 х = = 1

Проверка: х = 1 = 1 – 2 неверно, т.к.

х = 5 = 5 – 2 верно

2. Использование равносильных переходов.

Примеры решения уравнений

1. = х – 2

Ответ: х = 5.

3. Умножение левой части на сопряженное выражение.

Если в левой части иррационального уравнения сумма или разность корней, а подкоренное выражение — линейная функция одинаковыми линейными коэффициентами, а в правой части некоторое число, то левую и правую части уравнения умножают на выражение, сопряженное выражению в левой части ( и — сопряженные)

Решить уравнение:

( )() = 4()

х + 7 — х + 1 = 4( )

4( ) = 8

тогда имеем

Проверка:

3 + 1 = 4 верно Ответ : х = 2

4. Введение новой переменной.

1. Решить уравнение: ( х + 1) + 2

Введем новую переменную , t 0

х + 1 = t , тогда

t + 2 t = 15

t + 2 t – 15 = 0 решая, получим t = — 5 t = 3

х + 1 = 9

х = 8

х =

х = —

Ответ: х =

х =

2. Найти корни уравнения: х -3х – 18 + 4

Пусть = t , t 0, тогда

х -3х – 18 = t — 12

данное уравнение имеет вид: t + 4 t — 12 = 0 решая его, имеем:

Д = в— 4 ас = 16 + 4∙ 12 = 64

т. к. t 0 то t = 2 .

Тогда имеем :

х — 3х – 6 = 4

х — 3х – 10 = 0, решая квадратное уравнение получаем

Выполнив проверку, получаем корни уравнения.

Ответ: х = 5; х = 2

5. Решить уравнение:

Ни один из корней и не может принимать отрицательных значений. Поэтому ни при каких действительных значениях переменной х сумма корней не может равняться – 2.

Ответ: корней нет.

Заключение и выводы

Итак, уравнения, которые содержат переменную под знаком корня, называются иррациональными. Иррациональные уравнения решаются в основном возведением обеих частей уравнения в квадрат или введением новой переменной.

Данная исследовательская работа познакомила меня с новыми уравнениями, которые имеют название иррациональные. Также я узнала методы их решения и научилась решать иррациональные уравнения этими методами.

Надеюсь, что это мне пригодится для дальнейшей учебы в старших классах.

1) А.Г.Мордкович. Алгебра 8 класс. Учебник для общеобразовательных учреждений — Москва: Издательство “Мнемозина”, 2015

2) А.И.Макушевич. Детская энциклопедия – Москва: Издательство “Педагогика”, 1972.

3) А.П.Савин. Энциклопедический словарь юного математика – Москва: Издательство “Педагогика”, 1989.

4) А.И. Замыслова. Подготовка к экзаменам. Ростов — на –Дону «Феникс»

Содержание

Научно-исследовательская работа по теме » Решение иррациональных уравнений»
Министерство образования и науки
Гипотеза исследования- выбор рационального способа решения является эффективным методом решения иррационального уравнения
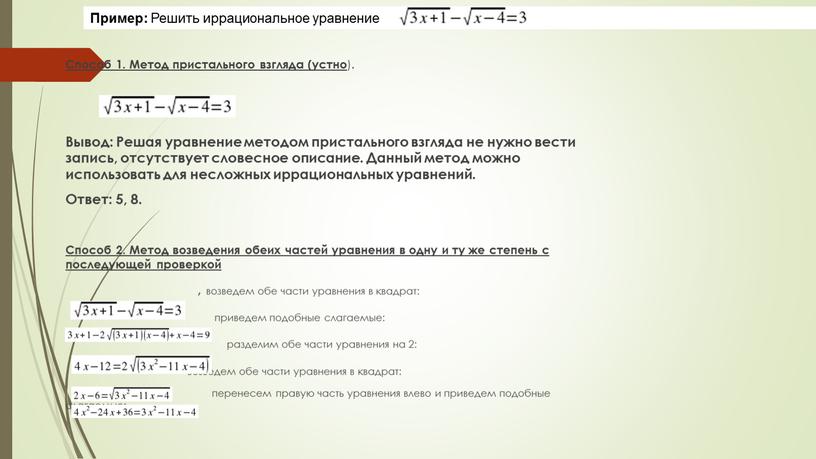
Способ 1. Метод пристального взгляда (устно )
Проверка: 1) Значит, число 5 является корнем уравнения
По теореме Виета: Ответ: 5; 8.
Способы решения иррациональных уравнений
📺 Видео

Видео:Иррациональные уравнения и их системы. 11 класс.Скачать

Научно-исследовательская работа по теме » Решение иррациональных уравнений»

Видео:СУПЕР ЛАЙФХАК — Как решать Иррациональные УравненияСкачать

Министерство образования и науки

Министерство образования и науки Республики Башкортостан ГАУ ДПО Институт развития образования Республики Башкортостан Конкурс исследовательских работ в рамках Малой академии наук Школьников Республики Башкортостан Секция: “Прорыв в науку”

Тема научно-исследовательской работы
Решение иррациональных уравнений

Ибрагимова Алина Наильевна
Учащаяся 10 «А» класса Муниципального Бюджетного общеобразовательного учреждения
Средняя общеобразовательная школа №2
Научный руководитель : Прокаева Светлана Ивановна
Учитель математики

Видео:Как решать уравнение с корнями Иррациональное уравнение Как решать уравнение с корнем х под корнемСкачать

Гипотеза исследования- выбор рационального способа решения является эффективным методом решения иррационального уравнения

Гипотеза исследования- выбор рационального способа решения является эффективным методом решения иррационального уравнения

Цель: рассмотреть несколько методов решения одного иррационального уравнения

Задачи: Показать, что иррациональные уравнения можно решить различными способами

Актуальность работы заключается в том, что решая одну задачу различными методами, можно путем сравнений выяснить, какой из них короче, а какой эффективнее, что позволяет успешно решать иррациональные уравнения различными способами.

Интерес к этой теме возник у меня совершенно случайно. Однажды, на одном из уроков математики нам предложили перечень иррациональных уравнений, и мы должны были к каждому подобрать свой способ решения. Должна отметить, что тема «Иррациональные уравнения» не вызывали у меня особых трудностей при изучении, но на этом уроке я поняла, что некоторые уравнения ставят меня в тупик. Например, уравнения, которые решаются с помощью введения новых переменных. Видя, как я увлеклась этой работой, наш учитель предложила мне обобщить эту тему и представить полный перечень методов решения иррациональных уравнений.

Видео:Уравнения с корнем. Иррациональные уравнения #shortsСкачать

Способ 1. Метод пристального взгляда (устно )

Способ 1. Метод пристального взгляда (устно).

Вывод: Решая уравнение методом пристального взгляда не нужно вести запись, отсутствует словесное описание. Данный метод можно использовать для несложных иррациональных уравнений.
Ответ: 5, 8.

Способ 2. Метод возведения обеих частей уравнения в одну и ту же степень с последующей проверкой
, возведем обе части уравнения в квадрат:
приведем подобные слагаемые:
разделим обе части уравнения на 2:
возведем обе части уравнения в квадрат:
перенесем правую часть уравнения влево и приведем подобные слагаемые:

Пример: Решить иррациональное уравнение

Видео:8 класс, 38 урок, Иррациональные уравненияСкачать

Проверка: 1) Значит, число 5 является корнем уравнения

решим квадратное уравнение:

Значит, число 5 является корнем уравнения.

Значит, число 8 является корнем уравнения.

Уравнение имеет два решения 5 и 8.

Вывод: При решении уравнений данным методом необходимо вести словесную запись, что делает решение понятным и доступным. Однако обязательная проверка иногда бывает громоздкой и занимает много времени. Этот метод можно использовать для несложных иррациональных уравнений, содержащих 1-2 радикала.

Способ 3. Метод равносильных преобразований

Видео:Алгебра 10 класс (Урок№20 - Иррациональные уравнения и неравенства.)Скачать

По теореме Виета: Ответ: 5; 8.

По теореме Виета:

Вывод: При решении уравнений данным методом нужно четко знать, когда ставить знак системы, а когда совокупности. Громоздкость записи, различные комбинации знаков системы и совокупности не редко приводят к ошибкам. Однако, последовательность равносильных переходов, четкая логическая запись без словесного описания, не требующая проверки, являются бесспорными плюсами данного способа.

Способ 4. Функционально графический метод

Видео:Иррациональные уравнения и их системы. Практическая часть. 1ч. 11 класс.Скачать

Способы решения иррациональных уравнений

Муниципальное общеобразовательное учреждение

Способы решения иррациональных уравнений

Выполнила: Егорова Ольга,

Раздел 1. Методы решения иррациональных уравнений…………………………………6

1.1 Решение иррациональных уравнений части С……….….….……………………21

Раздел 2.Индивидуальные задания……………………………………………. ………. 24

Математическое образование, получаемое в общеобразовательной школе, является важнейшим компонентом общего образования и общей культуры современного человека. Практически все, что окружает современного человека – это все так или иначе связано с математикой. А последние достижения в физике, технике и информационных технологиях не оставляют никакого сомнения, что и в будущем положение вещей останется прежним. Поэтому решение многих практических задач сводится к решению различных видов уравнений, которые необходимо научиться решать. Одним из этих видов являются иррациональные уравнения.

Уравнение, содержащее неизвестное (либо рациональное алгебраическое выражение от неизвестного) под знаком радикала, называют иррациональным уравнением. В элементарной математике решения иррациональных уравнений отыскивается в множестве действительных чисел.

Всякое иррациональное уравнение с помощью элементарных алгебраических операций (умножение, деление, возведение в целую степень обеих частей уравнения) может быть сведено к рациональному алгебраическому уравнению. При этом следует иметь в виду, что полученное рациональное алгебраическое уравнение может оказаться неэквивалентным исходному иррациональному уравнению, а именно может содержать «лишние» корни, которые не будут корнями исходного иррационального уравнения. Поэтому, найдя корни полученного рационального алгебраического уравнения, необходимо проверить, а будут ли все корни рационального уравнения корнями иррационального уравнения.

В общем случае трудно указать какой-либо универсальный метод решения любого иррационального уравнения, так как желательно, чтобы в результате преобразований исходного иррационального уравнения получилось не просто какое-то рациональное алгебраическое уравнение, среди корней которого будут и корни данного иррационального уравнения, а рациональное алгебраическое уравнение образованное из многочленов как можно меньшей степени. Желание получить то рациональное алгебраическое уравнение, образованное из многочленов как можно меньшей степени, вполне естественно, так как нахождение всех корней рационального алгебраического уравнения само по себе может оказаться довольно трудной задачей, решить которую полностью мы можем лишь в весьма ограниченном числе случаев.

Виды иррациональных уравнений

Решение иррациональных уравнений четной степени всегда вызывает больше проблем, чем решение иррациональных уравнений нечетной степени. При решении иррациональных уравнений нечетной степени изменение ОДЗ не происходит. Поэтому ниже будут рассматриваться иррациональные уравнения, степень которых является четной. Существует два вида иррациональных уравнений:

2..

Рассмотрим первый из них.

ОДЗ уравнения: f(x) ≥ 0. В ОДЗ левая часть уравнения всегда неотрицательна – поэтому решение может существовать только тогда, когда g(x) ≥ 0. В этом случае обе части уравнения неотрицательны, и возведение в степень 2n дает равносильное уравнение. Мы получаем, что

Обратим внимание на то, что при этом ОДЗ выполняется автоматически, и его можно не писать, а условие g(x) ≥ 0 необходимо проверять.

Примечание: Это очень важное условие равносильности. Во-первых, оно освобождает учащегося от необходимости исследовать, а после нахождения решений проверять условие f(x) ≥ 0 – неотрицательности подкоренного выражения. Во-вторых, акцентирует внимание на проверке условия g(x) ≥ 0 – неотрицательности правой части. Ведь после возведения в квадрат решается уравнение т. е. решаются сразу два уравнения (но на разных промежутках числовой оси!):

1. — там, где g(x) ≥ 0 и

2. — там, где g(x) ≤ 0.

Между тем многие, по школьной привычке находить ОДЗ, поступают при решении таких уравнений ровно наоборот:

а) проверяют, после нахождения решений, условие f(x) ≥ 0 (которое автоматически выполнено), делают при этом арифметические ошибки и получают неверный результат;

б) игнорируют условие g(x) ≥ 0 — и опять ответ может оказаться неверным.

Примечание: Условие равносильности особенно полезно при решении тригонометрических уравнений, в которых нахождение ОДЗ связано с решение тригонометрических неравенств, что гораздо сложнее, чем решение тригонометрических уравнений. Проверку в тригонометрических уравнениях даже условия g(x) ≥ 0 не всегда просто сделать.

Рассмотрим второй вид иррациональных уравнений.

. Пусть задано уравнение . Его ОДЗ:

В ОДЗ обе части неотрицательны, и возведение в квадрат дает равносильное уравнение f(x) = g(x). Поэтому в ОДЗ или

При таком способе решения достаточно проверить неотрицательность одной из функций – можно выбрать более простую.

Раздел 1. Методы решения иррациональных уравнений

1 метод. Освобождение от радикалов путем последовательного возведения обеих частей уравнения в соответствующую натуральную степень

Наиболее часто применяемым методом решения иррациональных уравнений является метод освобождения от радикалов путем последовательного возведения обеих частей уравнения в соответствующую натуральную степень. При этом следует иметь в виду, что при возведении обеих частей уравнения в нечетную степень полученное уравнение, эквивалентное исходному, а при возведении обеих частей уравнения в четную степень полученное уравнение будет, вообще говоря, неэквивалентным исходному уравнению. В этом легко убедиться, возведя обе части уравнения в любую четную степень. В результате этой операции получается уравнение , множество решений которого представляет собой объединение множеств решений: и . Однако, несмотря на этот недостаток, именно процедура возведения обеих частей уравнения в некоторую (часто четную) степень является самой распространенной процедурой сведения иррационального уравнения к рациональному уравнению.

, где — некоторые многочлены. В силу определения операции извлечения корня в множестве действительных чисел допустимые значения неизвестного определяются условиями . Возведя обе части этого уравнения в квадрат, получим уравнение .

После повторного возведения в квадрат уравнение превращается в алгебраическое уравнение .

Так как обе части 1 уравнения возводились в квадрат, может оказаться, что не все корни 2 уравнения будет являться решениями исходного уравнения, необходима проверка корней.

Возведя обе части уравнения в квадрат, получим уравнение 5х + 1 = х -1, т. е. уравнение х2 – 7х = 0, являющееся следствием исходного уравнения. Найдем его корни: х1 = 0 и х2 = 7. Подставим найденные числа в исходное уравнение. Пусть х = 0. Тогда левая часть уравнения равна 1, а правая -1. Поскольку 1 ≠ -1, то х = 0 не является корнем исходного уравнения. Пусть х = 7. тогда исходное уравнение обращается в верное числовое тождество 6 = 6. поэтому х = 7 – единственный корень данного уравнения.

Возводя обе части уравнения в куб, получим

Учитывая, что получим уравнение, которое является следствием исходного:(Последнее уравнение может иметь корни, которые, вообще говоря, не являются корнями уравнения ).

Возводим обе части этого уравнения в куб: . Перепишем уравнение в виде х3 – х2 = 0 ↔ х1 = 0, х2 = 1. проверкой устанавливаем, что х1 = 0 – посторонний корень уравнения (-2 ≠ 1), а х2 = 1 удовлетворяет исходному уравнению.

2 метод. Замена смежной системой условий

При решении иррациональных уравнений, содержащих радикалы четного порядка, в ответах могут появится посторонние корни, выявить которые не всегда просто. Чтобы легче было выявить и отбросить посторонние корни, в ходе решений иррациональных уравнений его сразу же заменяют смежной системой условий. Дополнительные неравенства в системе фактически учитывают ОДЗ решаемого уравнения. Можно находить ОДЗ отдельно и учитывать его позднее, однако предпочтительнее применять именно смешанные системы условий: меньше опасность что-то забыть, не учесть в процессе решения уравнения. Поэтому в некоторых случаях рациональнее использовать способ перехода к смешанным системам.

Решить уравнение:

Данное уравнение равносильно системе

Ответ: — единственный корень уравнения.

Решить уравнение:

Данное уравнение равносильно системе

Ответ: уравнение решений не имеет.

3 метод. Использование свойств корня n-ой степени

При решении иррациональных уравнений используются свойства корня n-ой степени. Арифметическим корнем n-й степени из числа а называют неотрицательное число, n-я степень числа которого равна а. Если n – четное(2n), то а ≥ 0, в противном случае корень не существует. Если n – нечетное(2n+1), то а – любое и = — . Функции являются возрастающими.

Свойства корня n-й степени для любого натурального n: Пусть f и g — некоторые функции, Тогда:

Применяя любую из этих формул, формально (без учета указанных ограничений), следует иметь ввиду, что ОДЗ левой и правой частей каждой из них могут быть различными. Например, выражение определено при f ≥ 0 и g ≥ 0, а выражение — как при f ≥ 0 и g ≥ 0, так и при f ≤ 0 и g ≤ 0.

Для каждой из формул 1-5 (без учета указанных ограничений) ОДЗ правой ее части может быть шире ОДЗ левой. Отсюда следует, что преобразования уравнения с формальным использованием формул 1-5 «слева — направо» (как они написаны) приводят к уравнению, являющемуся следствием исходного. В этом случае могут появится посторонние корни исходного уравнения, поэтому обязательным этапом в решении исходного уравнения является проверка.

Преобразования уравнений с формальным использованием формул 1-5 «справа – налево» недопустимы, так как возможно суждение ОДЗ исходного уравнения, а следовательно, и потеря корней.

Решить иррациональное уравнение:

Используя формулы 4 и 5, получим уравнение,

являющееся следствием исходного. Решение этого уравнения сводится к решению совокупности уравнений .

Из первого уравнения этой совокупности находим . Из второго следует, что откуда находим . Таким образом корнями данного уравнения могут быть только числа (-1) и (-2). Проверка показывает, что оба найденных корня удовлетворяют данному уравнению.

Решите уравнение: .

Решение: на основании тождеств первое слагаемое заменить на . Заметить, что как сумма двух неотрицательных чисел левой части. «Снять» модуль и после приведения подобных членов решить уравнение. Так как , то получаем уравнение . Так как и , то и . Поэтому и, значит, . Так как , то и поэтому

4 метод. Введения новых переменных

Другим примером решения иррациональных уравнений является способ введения новых переменных, относительно которых получается либо более простое иррациональное уравнение, либо рациональное уравнение.

Решение иррациональных уравнений путем замены уравнения его следствием (с последующей проверкой корней) можно проводить следующим образом:

1. Найти ОДЗ исходного уравнения.

2. Перейти от уравнения к его следствию.

3. Найти корни полученного уравнения.

4. Проверить, являются ли найденные корни корнями исходного уравнения.

Проверка состоит в следующем:

А) проверяется принадлежность каждого найденного корня ОДЗ исходного уравнения. Те корни, которые не принадлежат ОДЗ, являются посторонними для исходного уравнения.

Б) для каждого корня, входящего в ОДЗ исходного уравнения, проверяется, имеют ли одинаковые знаки левая и правая части каждого из уравнений, возникающих в процессе решения исходного уравнения и возводимых в четную степень. Те корни, для которых части какого-либо возводимого в четную степень уравнения имеют разные знаки, являются посторонними для исходного уравнения.

В) только те корни, которые принадлежат ОДЗ исходного уравнения и для которых обе части каждого из уравнений, возникающих в процессе решения исходного уравнения и возводимых в четную степень, имеют одинаковые знаки, проверяются непосредственной подстановкой в исходное уравнение.

Такой метод решения с указанным способом проверки позволяет избежать громоздких вычислений в случае непосредственной подстановки каждого из найденных корней последнего уравнения в исходное.

Решить иррациональное уравнение:

Множество допустимых значений этого уравнения:

Положив , после подстановки получим уравнение

или эквивалентное ему уравнение

которое можно рассматривать как квадратное уравнение относительно. Решая это уравнение, получим

Следовательно, множество решений исходного иррационального уравнения представляет собой объединение множеств решений следующих двух уравнений:

, .

Возведя обе части каждого из этих уравнений в куб, получим два рациональных алгебраических уравнения:

, .

Решая эти уравнения, находим, что данное иррациональное уравнение имеет единственный корень х = 2 (проверка не требуется, так как все преобразования равносильны).

Решить иррациональное уравнение:

Обозначим 2×2 + 5x – 2 = t. Тогда исходное уравнение примет вид . Возведя обе части полученного уравнения в квадрат и приведя подобные члены, получим уравнение , являющееся следствием предыдущего. Из него находим t = 16.

Возвращаясь к неизвестному х, получим уравнение 2×2 + 5x – 2 = 16, являющееся следствием исходного. Проверкой убеждаемся, что его корни х1 = 2 и х2 = — 9/2 являются корнями исходного уравнения.

Ответ: х1 = 2, х2 = -9/2.

5 метод. Тождественное преобразование уравнения

При решении иррациональных уравнений не следует начинать решение уравнение с возведения обеих частей уравнений в натуральную степень, пытаясь свести решение иррационального уравнения к решению рационального алгебраического уравнения. Сначала необходимо посмотреть, нельзя ли сделать какое-нибудь тождественное преобразование уравнения, которое может существенно упростить его решение.

Множество допустимых значений данного уравнения:. Сделаем следующие преобразования данного уравнения:

Разделим данное уравнение на .

Далее, записывая уравнение в виде

, получим:

При а =0 уравнение решений иметь не будет; при уравнение может быть записано в виде

;

при данное уравнение решений не имеет, так как при любом х, принадлежащем множеству допустимых значений уравнения, выражение, стоящее в левой части уравнения, положительно;

при уравнение имеет решение

Принимая во внимание, что множество допустимых решений уравнения определяется условием , получаем окончательно:

При решением этого иррационального уравнения будет .

При всех остальных значениях х уравнение решений не имеет, т. е. множество его решений – пустое множество.

Ответ: При решением уравнения будет . При всех остальных значениях х уравнение решений не имеет.

Решить иррациональное уравнение: .

Решим данное уравнение с помощью тождественных преобразований:

Решение квадратного уравнения системы дает два корня: х1 = 1 и х2 = 4. первый из полученных корней не удовлетворяет неравенству системы, поэтому х = 4.

1) Проведение тождественных преобразований позволяет обходиться без проверки.

2) Неравенство х – 3 ≥0 относится к тождественным преобразованиям, а не к области определения уравнения.

3) В левой части уравнения стоит убывающая функция, а в правой части этого уравнения расположена возрастающая функция. Графики убывающей и возрастающей функций в пересечении их областей определения могут иметь не больше одной общей точки. Очевидно, что в нашем случае х = 4 является абсциссой точки пересечения графиков.

6 метод. Использование области определения функций при решении уравнений

Этот метод наиболее результативен при решении уравнений, в состав которых входят функции в этом случае нужно перенести все члены уравнения в левую часть, рассмотреть функцию и найти ее область определения (f). При этом если Ø, то уравнение решений не имеет, если , то действительные решения данного уравнения находятся среди чисел ; необходимо проверить, какие из них являются решениями данного уравнения; если , то нужно проверить верно ли уравнение на концах промежутка, причем, если а 0, то необходима проверка на промежутках (а;0) и [0;b).

Решить иррациональное уравнение:

Найдем область определения уравнения:

Возведем обе части уравнения в квадрат:

Повторное возведение в квадрат дает: Корни квадратного уравнения . Заметим, что решение исходного уравнения дает два корня, входящих в область определения. Проверка из-за громоздкости корней оказывается гораздо сложнее нахождения самих корней уравнения. Вместе с тем в левой части решаемого уравнения стоит сумма двух возрастающих функций, т. е. функция возрастающая. Она может принимать х ≥ 0,5 значение, равное 4, единственный раз, поскольку при ч = 0,5 левая часть уравнения имеет значение , а с ростом х значение функции возрастает. Очевидно, что х1 не является корней уравнения, так как первый радикал левой части уравнения уже больше 10, а второй радикал положителен.

Ответ:

Решить иррациональное уравнение:

. Рассмотрим функцию и найдем ее область определения D(f): .

Проверим, являются ли эти значения корнями данного уравнения: если х = 1, то и равенство неверно, х = 1 не является корнем уравнения; если, то является корнем данного уравнения.

7 метод. Использование области значений функций при решении уравнений (метод оценки)

Наиболее результативным данный метод является при решении уравнений, в состав которых входят функции, области значений которых ограничены, а именно: .

При каких значениях а уравнение имеет хотя бы один корень.

Рассмотрим функции

Так как , то данное уравнение равносильно системе

Решая первое уравнение системы, получим

Подставим найденное решение во второе уравнение системы

Отсюда следует, что при , данная система уравнений, а значит, и данное уравнение имеет хотя бы один корен.

Ответ: х =

Найдите наименьшее целое значение функции.

Выражаем подкоренное выражение через cos2 x: Находим множество значений подкоренного выражения: так как cos2 x принимает все значения от 0 до 1, то принимает все значения от 1 до 4. Находим множество Е(у) значений функции и выбираем из него наименьшее целое число: принимает все значения от 1 до 2, и Е(у) = [2.5;5]. Наименьшее целое число в Е(у) равно 3.

8 метод. Применение производной при решении иррациональных уравнений

Чаще всего при решении уравнений с помощью метода применения производной используется метод оценки.

Решите уравнение: (1)

Решение: Так как , уравнение (1) можно преобразовать к виду , или (2). Рассмотрим функцию . Это нечетная функция, так как . Поэтому уравнение (2) можно последовательно преобразовать так как: , так как — нечетная функция. Далее, при всех и, следовательно, возрастает. Поэтому уравнение равносильно уравнению , имеющему корень , являющимся корнем исходного уравнения.

Ответ:

Решить иррациональное уравнение:

Область определения функции есть отрезок [2;4]. Найдем наибольшее и наименьшее значение значения этой функции на отрезке [2;4]. Для этого найдем производную функции f(x):

Значение производной обращается в 0 при . Найдем значения функции f(x) на концах отрезка [2;4] и в точке : Значит, Но и, следовательно, равенство возможно лишь при условии откуда . Проверка показывает, что число 3 – корень данного уравнения.

9 метод. Функциональный

На экзаменах иногда предлагают решить уравнения, которые можно записать в виде , где — это некоторая функция.

Например, некоторые уравнения: 1) 2) . Действительно, в первом случае , во втором случае . Поэтому решать иррациональные уравнения с помощью следующего утверждения: если функция строго возрастает на множестве Х и для любого , то уравнения и т. д. равносильны на множестве Х .

Решить иррациональное уравнение: (1)

Функция строго возрастает на множестве R, и для любого . Тогда на основании вышеизложенного утверждения уравнение (1) равносильно уравнению А это уравнение, в сою очередь, равносильно уравнению которое имеет единственный корень Следовательно, и равносильное ему уравнение (1) также имеет единственный корень

Решить иррациональное уравнение: (1)

В силу определения квадратного корня получаем, что если уравнение (1) имеет корни, то они принадлежат множеству Поэтому далее будем рассматривать уравнение (1) на этом множестве. На нем уравнение (1) можно переписать в виде

. (2)

Рассмотрим функцию на множестве Х. Ясно, что строго возрастает на этом множестве для любого . Уравнение (2) можно записать в виде , поэтому на основании известного уже нам утверждения уравнение (2) равносильно на множестве Х уравнению которое имеет единственный корень Следовательно, и равносильное ему на множестве Х уравнение (1) имеет единственный корень

Ответ:

10 метод. Графический

При решении иррациональных уравнений иногда полезно рассмотреть эскиз графиков их правой и левой частей в одной и той же системе координат. Тогда этот эскиз графиков поможет выяснить, на какие множества надо разбить числовую ось, чтобы на каждом из них решение уравнения было очевидно.

При каких значениях a найдутся вещественные x и y, удовлетворяющие уравнению

Решение: Данное уравнение равносильно смешанной системе

Длина отрезка PK равна поэтому окружность, заданная уравнением, и полуплоскость, заданная неравенством, имеют общие точки, если радиус окружности, равный будет больше или равен OP, т. е. . Отсюда найдем a,

Ответ:

Решить графически уравнение:

Для графического решения, преобразуем уравнение к виду:

Теперь ясно, что надо построить графики функций и .

Графиком функции является ветвь параболы, направленная.

влево вдоль оси OX, с вершиной в точке (25; 0).

Построение графика функции можно выполнить в несколько этапов:

1) построить график функции , которым является ветвь параболы, направленная вдоль оси OX вправо, лежащая выше оси OX, с вершиной в точке ;

2) эту ветвь надо перенести параллельно самой себе вдоль оси OY на 2 единицы вниз, тогда получим график функции ;

3) полученную кривую, надо симметрично отразить в оси OX, тогда получится график функции . Графики не имеют точек пересечения, значит, уравнение не имеет решений.

Ответ: корней нет.

1.1 Решение иррациональных уравнений части С

Для решения иррациональных уравнений , т. е. уравнений части С Единого Государственного Экзамена нужно использовать несколько методов сразу.

Решите уравнение:

Решение: Если

Ответ: , , .

Найдите наименьшее целое значение функции .

Решение: . Так как принимает все значения от 0 до 1, то принимает все значения от 1 до 4. Значит, принимает все значения от 1 до 2, и . Наименьшее целое число в равно 3.

Найдите множество значений функции: .

Решение: Так как .

Поэтому .

Так как — убывающая и непрерывная функция, то и.

Следовательно,

Ответ:

При каком целом положительном х значение выражения

ближе всего к -0,7?

1) Преобразовываем выражение к максимально простому виду (к функции y = y(x)).

2) Функцию y = y(x) исследовать на монотонность и найти целые положительные числа, ближайшие к корню уравнения y(x) = -0,7.

3) Произвести отбор среди найденных целых положительных чисел.

1) ОДЗ выражения есть множество По условию х > 0, поэтому можно считать, что При х = 5 знаменатель второго сомножителя обращается в нуль. Значит, x > 5.