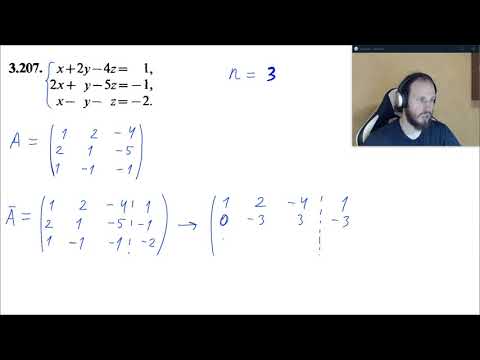Исследовать нетривиальные решения однородная система уравнений

Решением системы называется совокупность n значений неизвестных

при подстановке которых все уравнения системы обращаются в тождества.

Система линейных уравнений может быть записана в матричном виде:

где A — матрица системы, b — правая часть, x — искомое решение, A_p — расширенная матрица системы:

.

Система, имеющая хотя бы одно решение, называется совместной; система, не имеющая ни одного решения — несовместной.

Однородной системой линейных уравнений называется система, правая часть которой равна нулю:

Матричный вид однородной системы: Ax=0.

Однородная система в с е г д а с о в м е с т н а, поскольку любая однородная линейная система имеет по крайней мере одно решение:

Если однородная система имеет единственное решение, то это единственное решение — нулевое, и система называется тривиально совместной. Если же однородная система имеет более одного решения, то среди них есть и ненулевые и в этом случае система называется нетривиально совместной.

Доказано, что при m=n для нетривиальной совместности системы необходимо и достаточно, чтобы определитель матрицы системы был равен нулю.

ПРИМЕР 1. Нетривиальная совместность однородной системы линейных уравнений с квадратной матрицей.

Применив к матрице системы алгоритм гауссова исключения, приведем матрицу системы к ступенчатому виду

.

Для того, чтобы однородная система была нетривиально совместна, необходимо и достаточно, чтобы ранг r матрицы системы был меньше числа неизвестных n.

ПРИМЕР 2. Нетривиальная совместность однородной системы трех линейных уравнений с четырьмя неизестными.

Если однородная система нетривиально совместна, то она имеет бесконечное множество решений, причем линейная комбинация любых решений системы тоже является ее решением.
Доказано, что среди бесконечного множества решений однородной системы можно выделить ровно n-r линейно независимых решений.
Совокупность n-r линейно независимых решений однородной системы называется фундаментальной системой решений. Любое решение системы линейно выражается через фундаментальную систему. Таким образом, если ранг r матрицы A однородной линейной системы Ax=0 меньше числа неизвестных n и векторы
e₁ , e₂ , . e_n-r образуют ее фундаментальную систему решений (Ae_i =0, i=1,2, . n-r), то любое решение x системы Ax=0 можно записать в виде

где c₁ , c₂ , . c_n-r — произвольные постоянные. Записанное выражение называется общим решением однородной системы.

Исследовать однородную систему — значит установить, является ли она нетривиально совместной, и если является, то найти фундаментальную систему решений и записать выражение для общего решения системы.

Исследуем однородную систему методом Гаусса.

матрица исследуемой однородной системы, ранг которой r

Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter

Видео:Видеоурок "Однородные системы линейных уравнений"Скачать

Как найти нетривиальное и фундаментальное решение системы линейных однородных уравнений

Пример 2 . Найти общее решение и фундаментальную систему решений системы
Решение.

Задание . Исследовать и решить систему линейных уравнений.
Пример 4

Задание . Найти общее и частное решения каждой системы.
Решение. Выпишем основную матрицу системы:

Приведем матрицу к треугольному виду. Будем работать только со строками, так как умножение строки матрицы на число, отличное от нуля, и прибавление к другой строке для системы означает умножение уравнения на это же число и сложение с другим уравнением, что не меняет решения системы.
Умножим 2-ую строку на (-5). Добавим 2-ую строку к 1-ой:

Умножим 2-ую строку на (6). Умножим 3-ую строку на (-1). Добавим 3-ую строку к 2-ой:

В матрице B 1-ая и 2-ая строки пропорциональны, следовательно, одну из них, например 1-ю, можно вычеркнуть. Это равносильно вычеркиванию 1-го уравнения системы, так как оно является следствием 2-го.

Найдем ранг матрицы.

Выделенный минор имеет наивысший порядок (из возможных миноров) и отличен от нуля (он равен произведению элементов, стоящих на обратной диагонали), следовательно rang(A) = 2.
Этот минор является базисным. В него вошли коэффициенты при неизвестных x₁,x₂, значит, неизвестные x₁,x₂ – зависимые (базисные), а x₃,x₄,x₅ – свободные.
Преобразуем матрицу, оставляя слева только базисный минор.

Система с коэффициентами этой матрицы эквивалентна исходной системе и имеет вид:
22x₂ = 14x₄ — x₃ — 24x₅
6x₁ + 2x₂ = — 2x₄ — 11x₃ — 6x₅
Методом исключения неизвестных находим нетривиальное решение:
Получили соотношения, выражающие зависимые переменные x₁,x₂ через свободные x₃,x₄,x₅, то есть нашли общее решение:
x₂ = 0.64x₄ — 0.0455x₃ — 1.09x₅
x₁ = — 0.55x₄ — 1.82x₃ — 0.64x₅
Находим фундаментальную систему решений, которая состоит из (n-r) решений.
В нашем случае n=5, r=2, следовательно, фундаментальная система решений состоит из 3-х решений, причем эти решения должны быть линейно независимыми.
Чтобы строки были линейно независимыми, необходимо и достаточно, чтобы ранг матрицы, составленной из элементов строк, был равен количеству строк, то есть 3.
Достаточно придать свободным неизвестным x₃,x₄,x₅ значения из строк определителя 3-го порядка, отличного от нуля, и подсчитать x₁,x₂.
Простейшим определителем, отличным от нуля, является единичная матрица.

Задача . Найти фундаментальный набор решений однородной системы линейных уравнений. Решение

Задача . Найти общее решение системы. Проанализировать его структуру (указать базис пространства решений однородной системы, установить размерность пространства). Решение Пример 3
Пример 4

Видео:ФСР. Система однородных уравнений. Общее решениеСкачать

4.2.3 Системы линейных однородных уравнений

Рассмотрим систему вида

, (1)

Где или .

Однородная система линейных уравнений (1) всегда совместна, так как . Она заведомо имеет решение, состоящее из нулей , которое называется тривиальным.

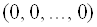
В каких случаях существует нетривиальное решение?

Теорема. Для того чтобы система (1) имела нетривиальные решения, необходимо и достаточно, чтобы ранг ее матрицы был меньше числа неизвестных.

Действительно, в этом случае есть свободные неизвестные, которым можно придавать любые, в том числе и ненулевые, значения.

Выделим частный случай систем (1), когда .

Теорема. Система (1) в случае имеет нетривиальное решение тогда и только тогда, когда определитель этой системы равен нулю.

Системы линейных однородных уравнений обладают важным свойством, которое сформулируем в виде теоремы.

Теорема. Любая линейная комбинация решений системы (1) также является решением этой системы.

Возникает вопрос, можно ли подобрать такую совокупность решений системы (1), чтобы любое решение системы можно было бы найти как линейную комбинацию этих решений? Такая совокупность решений существует и носит название фундаментальной.

Определение. Совокупность решений системы линейных однородных уравнений (1) называется фундаментальной системой решений, если эта совокупность состоит из линейно независимых решений и любое решение системы (1) является линейной комбинацией этих решений.

Теорема. Если ранг 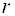матрицы системы (1) меньше числа n неизвестных, то существует фундаментальная система решений, состоящая из решений.

Пример 22. Найти общее решение и какую-нибудь фундаментальную систему решений для системы

Решение. Алгоритм решения такой же, как и для систем линейных неоднородных уравнений.

Оперируя только со строками, находим ранг матрицы, базисный минор; объявляем зависимые и свободные неизвестные и находим общее решение.

Первая и вторая строки пропорциональны, одну из них вычеркнем:

.

Зависимые переменные – , свободные – . Из первого уравнения находим , тогда

; .

Общее решение имеет вид:

Находим фундаментальную систему решений, которая состоит из решений. В нашем случае , следовательно, фундаментальная система решений состоит из двух решений, причем эти решения должны быть линейно независимыми. Чтобы строки были линейно независимыми, необходимо и достаточно, чтобы ранг матрицы, составленной из элементов строк, был равен количеству строк, то есть 2. Достаточно придать свободным неизвестным и значения из строк определителя второго порядка, отличного от нуля, и подсчитать . Простейшим определителем, отличным от нуля, является .

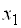
Таким образом, первое решение: , второе – .

Эти два решения составляют фундаментальную систему решений. Заметим, что фундаментальная система не единственна (определителей, отличных от нуля, можно составить сколько угодно).

Пример 22. Найти общее решение и фундаментальную систему решений системы

,

Отсюда следует, что ранг матрицы равен 3 и равен числу неизвестных. Значит, система не имеет свободных неизвестных, а поэтому имеет единственное решение – тривиальное.

Для самостоятельного решения.

1. Доказать, что система совместна.

Найти ее общее и частное решения, приняв в качестве свободных неизвестных и полагая .

Ответ: .

2. Образуют ли строки каждой из матриц 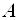и , где , , фундаментальную систему решений для системы

Ответ: строки матрицы 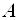не образуют фундаментальную систему решений, строки матрицы образуют.

3. Три прямые , , образуют треугольник. Охарактеризовать систему трех уравнений с точки зрения совместности и ранга матрицы коэффициентов.

Ответ выбрать из списка: 1) система совместна, ; 2) система несовместна, ; 3) совместна любая пара уравнений, .

📸 Видео

15. Однородная система линейных уравнений / фундаментальная система решенийСкачать

Неоднородная система линейных уравненийСкачать

Однородная система слау. Тривиальное решение. Ненулевое решениеСкачать

Математика без Ху!ни. Метод Гаусса.Скачать

Решение системы уравнений методом ГауссаСкачать

Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

§41 Решение систем линейных однородных уравненийСкачать

При каких λ однородная система уравнений имеет ненулевое решение?Скачать

Система линейных уравнений. Общее решение. Метод ГауссаСкачать

Решение однородных линейных систем. ТемаСкачать

Решение системы уравнений методом Крамера.Скачать

Лекция 13. Исследование систем линейных уравнений. Теорема Кронекера — Капелли.Скачать

Исследование систем линейных уравнений на совместностьСкачать

Фундаментальная система решений для однородной системы линейных уравненийСкачать

Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Решение однородных и неоднородных систем линейных уравнений. Нахождение ФСР.Скачать

Неоднородные системы линейных уравненийСкачать

Метод Гаусса решения систем линейных уравненийСкачать