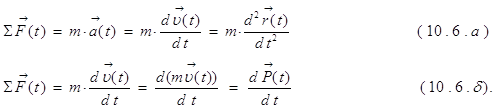Инвариантность уравнений классической механики относительно преобразований галилея (3 видео)

Инвариантность уравнений классической механики относительно преобразований галилея

1. Преобразования Галилея. Инвариантность уравнений классической механики относительно преобразования Галилея.

2. Основное уравнение молекулярно-кинетической теории идеального газа

3. При изохорном нагревании кислорода объемом 20 л давление газа изменилось на 0,1 МПа. Найти количество теплоты, сообщенное газу.

4. Пуля массой m=9 г, летящая горизонтально со скоростью V=500 м/с, попадает в баллистический маятник массой М=12 кг и застревает в нём. Определить максимальную высоту, на которую поднимается маятник после внедрения пули.

Содержание

Законы классической механики и их инвариантность относительно преобразований Галилея
Принцип относительности Галилея.
Наблюдатель на корабле.
Инвариантность законов механики.
🔍 Видео

Видео:Принцип относительности ГалилеяСкачать

Законы классической механики и их инвариантность относительно преобразований Галилея

10.3. Законы классической механики и их инвариантность относительно преобразований Галилея.

Создание основ классической механики завершается трудами И.Ньютона, сформулировавшего основные законы механики и открывшего закон всемирного тяготения. Классическая механика Ньютона базировалась на работах Галилея, Декарта, Паскаля, Гука и многих других.

Раздел механики, в котором изучаются причины движения тел, т.е. силы, вызывающие их движение, называется динамикой. Основные законы механики, сформулированные Ньютоном дошли почти без изменений до наших дней. Они известны из школьного курса физики. Напомним их.

Первый закон Ньютона. Всякое тело в инерциальной системе отсчета сохраняет состояние покоя или равномерного прямолинейного движения, пока воздействие со стороны других тел не заставит его изменить это состояние.

Второй закон Ньютона. Ускорение тела прямо пропорционально сумме сил, действующих на него и обратно пропорционально его массе. Запишем этот закон в векторной форме с учетом кинематических соотношений

В этих формулировках мы использовали понятие импульса или количества движения P = m×u, которое было введено Декартом. Закон Ньютона, записанный в виде (10.6.а) или (10.6.б) с математической точки зрения имеет вид дифференциального уравнения, т.е. уравнения в котором значение функции связывается со значением ее производной. Любая из формулировок (10.6.а,б) второго закона Ньютона называется основным уравнением динамики. Решение этого уравнения является основной задачей динамики. Основная задача динамики может быть поставлена в форме прямой и обратной задачи. В прямой задаче требуется по известному закону движения тела r(t) найти действующие на это тело силы. В обратной задаче по известной зависимости действующих сил от времени SF(t) требуется найти закон движения тела r(t). Различные формулировки (10.6) могут немного менять постановку основной задачи, как прямой, так и обратной. Однако, прямая задача всегда математически сводится к дифференцированию, а обратная — к интегрированию. Очевидно, что решение обратной задачи динамики должно быть значительно более трудоемким, чем прямой. Отметим также, что для решения обратной задачи требуется знать начальные условия, которых в зависимости от постановки задачи (в форме 10.6.а или 10.6.б) должно быть задано либо столько же, сколько и степеней свободы системы, либо вдвое больше.

Третий закон Ньютона. Силы, с которыми взаимодействуют тела равны по величине, противоположны по направления и направлены вдоль линии взаимодействия. Этот закон утверждает, что силовое воздействие на тело носит характер взаимодействия. Этот же закон утверждает, что взаимодействия всех тел являются центральными.

Закон всемирного тяготения, открытый Ньютоном, иногда называют четвертым законом Ньютона. Его открытие базируется на трудах выдающихся астрономов 16-17-х веков Н.Коперника и И.Кеплера. И.Кеплер на основании учении Коперника о гелиоцентрической системе мира сформулировал три закона движения планет. Эти законы были правильными, но, как показал впоследствии И.Ньютон, являлись частным случаем более общего закона всемирного тяготения. Законы Кеплера позволяли найти орбиты планет, периоды их обращения вокруг солнца и скорость движения планет по орбитам.

С позиций современной механики отметим, что второй закон Кеплера является следствием закона сохранения момента импульса, он справедлив для движения тела в поле любых центральных сил.

С использование введенного нами математического аппарата закон всемирного тяготения можно написать в виде:

, где G — гравитационная постоянная, m₁ и m₂ массы тел, единичный вектор, направленный вдоль линии взаимодействия, определяющий направление гравитационной силы .

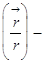
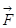
Тело, двигающееся прямолинейно и равномерно относительно системы отсчета К, вследствие уравнений (10.4) движется также прямолинейно и равномерно относительно системы отсчета К’. Это обозначает, что формулировка первого закона Ньютона во всех инерциальных системах отсчета одинакова (правильнее сказать, первый закон Ньютона справедлив во всех инерциальных системах отсчета). Отметим, что, уравнения (10.4) позволяют по одной известной инерциальной системе отсчета построить бесконечное множество других.

В системе координат К форма записи второго закона Ньютона определяется уравнениями (10.6). Поскольку, ускорение и масса инвариантны относительно преобразований Галилея, уравнение (10.6) одинаково записывается в различных инерциальных системах отсчета.

Поскольку, величина силы не меняется при переходе от одной инерциальной системы отсчета к другой, третий закон Ньютона тоже инвариантен относительно преобразований Галилея.

Четвертый закон не нуждается в доказательстве инвариантности относительно преобразований Галилея, поскольку расстояния, массы и силы не меняются при переходе из одной инерциальной системы отсчета в другую.

Таким образом, все законы Ньютона инвариантны относительно преобразований Галилея. Это значит, что они справедливы и записываются одинаковым образом во всех инерциальных системах отсчета.

Видео:Преобразования ГалилеяСкачать

Принцип относительности Галилея.

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: инерциальные системы отсчёта, принцип относительности Галилея.

Изучение теории относительности Эйнштейна мы начинаем с более глубокого рассмотрения принципа относительности Галилея. Это позволит нам лучше понять, каковы были предпосылки создания теории относительности.

Ключевую роль в механике и теории относительности играет понятие инерциальной системы отсчёта. Если вы забыли, что это такое, то обязательно прочитайте ещё раз Первый закон Ньютона.

В конце этой темы было кратко сказано о принципе относительности Галилея. Настало время поговорить о нём подробнее. В чём же суть данного принципа?

Видео:ЧК_МИФ ОСНОВАНИЯ СТО: ПРИНЦИП ОТНОСИТЕЛЬНОСТИ ГАЛИЛЕЯ И ПРЕОБРАЗОВАНИЯ ГАЛИЛЕЯСкачать

Наблюдатель на корабле.

Представьте себе, что вы находитесь в каюте корабля. Никакого движения в пространстве вы не ощущаете — вам кажется, что корабль стоит на месте. Но вас всё же интересует, покоится ли корабль или движется равномерно и прямолинейно. Можете ли вы установить это, не выглядывая в иллюминатор?

Допустим, что с данной целью вы производите всевозможные эксперименты, наблюдая различные механические явления в вашей каюте. Вы исследуете свободное падение тел, соскальзывание тела с наклонной плоскости, вращательное движение, колебания маятников, распространение звуковых волн. . . Вам детально известен ход этих явлений в неподвижной лаборатории на земле, и теперь вы пытаетесь найти какие-либо отклонения в их протекании, вызванные равномерным прямолинейным движением судна.

Никаких отклонений обнаружить не удастся! Поставив в каюте корабля любой механический эксперимент и сопоставив его с аналогичным экспериментом на земле, вы увидите, что полученные результаты не отличаются друг от друга. Например, вы бросаете мячик со скоростью 5 м/с под углом к горизонту относительно палубы. Оказывается, мячик на корабле опишет ровно ту же самую траекторию, что и на берегу при тех же начальных условиях (скорость и угол броска).

Равномерное прямолинейное движение корабля никак не сказывается на протекании механических явлений на этом корабле. Поэтому никакой опыт из механики, проведённый в лаборатории корабля, не в состоянии определить, покоится ли корабль или движется равномерно и прямолинейно.

Систему отсчёта, связанную с землёй, во многих ситуациях можно считать инерциальной.(Конечно, Земля совершает суточное вращение и движется вокруг Солнца, поэтому земная лаборатория будет иметь ускорение. Но во многих задачах этим ускорением можно пренебречь.) Система отсчёта корабля, движущаяся относительно земной системы отсчёта равномерно и прямолинейно, также будет инерциальной. Мы приходим к выводу, что с точки зрения механических явлений инерциальные системы отсчёта совершенно равноправны: никакой механический эксперимент не в состоянии выделить и сделать привилегированной какую-то одну инерциальную систему отсчёта по сравнению с остальными.

Это и есть принцип относительности, открытый Галилеем.

Принцип относительности Галилея. Всякое механическое явление при одних и тех же начальных условиях протекает одинаково в любой инерциальной системе отсчёта.

Видео:ЧК_МИФ НЕОБХОДИМОСТЬ ПЕРЕСМОТРА ОСНОВАНИЙ КЛАССИЧЕСКОЙ ФИЗИКИСкачать

Инвариантность законов механики.

Принцип относительности Галилея означает, что законы механики одинаковы во всех инерциальных системах отсчёта. А именно, математическая форма второго и третьего законов Ньютона не меняется при переходе от одной инерциальной системы отсчёта к другой. Давайте убедимся в этом непосредственно на следующем простом примере.

Рассмотрим две системы отсчёта: и . Координатные оси этих систем сонаправлены. Систему будем считать неподвижной. Система движется относительно неё с постоянной скоростью вдоль общего направления осей и (рис. 1 )

Инвариантность уравнений классической механики относительно преобразований галилея

Рис. 1. Система движется относительно системы

В тот момент, когда начала координат и совпадали, часы обеих систем были выставлены на ноль и запущены. Стало быть, часы в системах и идут синхронно, показывая одно и то же время . В момент времени расстояние равно .

Нас интересует, как описывается движение тела (для определённости называемого далее частицей) в системах отсчёта и .

Прежде всего, выясним, как связаны друг другом координаты частицы и моменты времени в обеих системах отсчёта.

Пусть в момент времени по часам частица имеет в системе координаты . Вообще, четвёрка чисел называется событием. Событие состоит в том, что в данной точке пространства в данный момент времени что-то происходит — вот, например, в точке с координатами в момент времени оказывается наша частица.

В системе это же событие описывается четвёркой чисел . А именно, местонахождение частицы в системе описывается координатами , а часы показывают при этом время .

Глядя на рис. 1 , совершенно ясно, что будет меньше на величину , координата совпадает с , а совпадает с . Кроме того, как уже было сказано, время на часах и одно и то же: .

Формулы (1) называются преобразованиями Галилея. Они связывают координаты и время одного и того же события, измеренные в разных инерциальных системах отсчёта: в движущейся системе и неподвижной системе .

Таким образом, преобразования Галилея в механике служат математическим описанием перехода от одной инерциальной системы отсчёта к другой. Рассмотрим некоторые следствия, вытекающие из преобразований Галилея.

Пусть наша частица имеет в системе скорость , а в системе — скорость . Как связаны между собой эти скорости? Дифференцируем первые три равенства (1) по времени (которое одинаково в обеих системах отсчёта):

Производные координат по времени — это проекции скоростей:

Три равенства (2) можно записать в виде одной векторной формулы:

Получился хорошо известный нам закон сложения скоростей: скорость тела относительно неподвижной системы отсчёта есть скорость тела относительно движущейся системы отсчёта плюс скорость движущейся системы относительно неподвижной. Мы видим, таким образом, что закон сложения скоростей в механике является следствием преобразований Галилея.

Дифференцируем по времени ещё раз — на сей раз соотношения (2) . Производная постоянной величины обращается в нуль, и мы получаем равенство ускорений:

Итак,
ускорение частицы одинаково во всех инерциальных системах отсчёта. Это ещё одно следствие преобразований Галилея.

Теперь запишем второй закон Ньютона для нашей частицы в системе :

При переходе в систему ускорение частицы , как мы выяснили, остаётся прежним. А что можно сказать об остальных двух величинах, входящих в (3) , — массе и силе?

Масса есть мера инертности тела; масса показывает, в какой степени тело «сопротивляется» изменению скорости. Но приращение скорости — нашей частицы будет одним и тем же в любой инерциальной системе отсчёта. Следовательно, масса частицы во всех инерциальных системах отсчёта одинакова.

Силы в механике зависят от расстояний между телами и, быть может, скоростей тел друг относительно друга. Но расстояние между двумя точками пространства одинаково во всех инерциальных системах отсчёта. Скорость одной частицы относительно другой также не зависит от того, в какой инерциальной системе отсчёта рассматривается движение. Стало быть, сила одинакова во всех инерциальных системах отсчёта.

Величины и соотношения, не меняющиеся при определённых условиях, часто называются инвариантными. Так, ускорение, масса и сила инвариантны относительно выбора инерциальной системы отсчёта. Поэтому второй и третий законы Ньютона во всех системах отсчёта имеют одинаковый вид, т. е. инвариантны относительно преобразований Галилея.

Законы механики инвариантны относительно преобразований Галилея — такова альтернативная формулировка принципа относительности Галилея. Подчеркнём, что речь идёт об инвариантности математической формы законов механики. В результате этой инвариантности одно и то же механическое явление, наблюдаемое при одних и тех же начальных условиях, будет протекать одинаково во всех инерциальных системах отсчёта