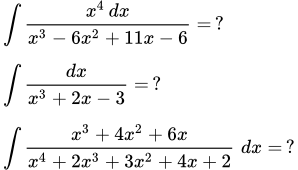Интеграл от дроби с квадратными уравнениями (4 видео)

Содержание

Интегрирование рациональных дробей
Алгоритм интегрирования рациональной дроби
Примеры интегрирования рациональных функций
Интегрирование рациональных функций и метод неопределённых коэффициентов
Алгоритм интегрирования рациональных функций
Алгоритм интегрирования рациональных функций
Шаг 1: разложение исходной дроби
Шаг 2: нахождение неопределённых коэффициентов
Шаг 3: нахождение интеграла исходной функции (дроби)
Примеры интегрирования рациональных функций (дробей)
Пример 1
Пример 2
Пример 3
🎬 Видео

Видео:Математика без Ху!ни. Метод неопределенных коэффициентов.Скачать

Интегрирование рациональных дробей

Рациональной дробью называется дробь вида

– многочлены степени m и n соответственно. Рациональная дробь называется правильной , если степень числителя меньше степени знаменателя (m Пример 1

Интегралы, содержащие в знаменателе квадратный трехчлен, можно вычислить, применяя прием выделения полного квадрата разности или суммы. Рассмотрим пример такого интеграла.

Алгоритм интегрирования рациональной дроби

1. Если дробь неправильная, надо выделить целую часть рациональной дроби, разделив числитель на знаменатель по правилу деления многочлена на многочлен, т.е. представить в виде:

2. Знаменатель разложим на простейшие сомножители: Q_n(x)

3. Представим дробь

виде суммы простейших дробей с неопределенными коэффициентами.

Приведем все дроби в разложении к общему знаменателю и приравняем числители в обеих частях равенства.
Составим систему уравнений, используя равенство многочленов, стоящих в числителе, приравнивая коэффициенты при одинаковых степенях x.
Решим систему уравнений, находя некоторые коэффициенты методом частных значений, полагая равным действительным корням знаменателя.
Подставим найденные коэффициенты A₁,A₂,…,C_s,D_s в разложение дроби.
Проинтегрируем простейшие дроби.

Видео:Интегрирование рациональных функций (дробей) ★ Найдите интеграл ∫((7x^3+3x^2-44x+21)/(x^2+x-6))dxСкачать

Примеры интегрирования рациональных функций

Пример 4.

Корни знаменателя: x=1, а x 2 +1 = 0 не имеет действительных корней.

Тогда разложение для данной дроби имеет вид:

Приводя полученные дроби к общему знаменателю, получим тождество:

Вычислим коэффициенты разложения, приравнивая коэффициенты при одинаковых степенях. Так как знаменатель имеет три действительных различных корня, то три коэффициента найдем методом частных значений.

Подставим найденные коэффициенты в разложение и проинтегрируем дроби.

Видео:5.1 Интегрирование функций, содержащих квадратный трехчлен. Часть 1Скачать

Интегрирование рациональных функций и метод неопределённых коэффициентов

Видео:8.2 Интегралы с корнем / интегралы с квадратным трехчленомСкачать

Алгоритм интегрирования рациональных функций

Рациональная функция — это дробь вида , числитель и знаменатель которой — многочлены или произведения многочленов.

Из урока «Интегрирование некоторых рациональных дробей и иррациональностей» известно, что рациональные дроби бывают неправильные, если степень многочлена в её числителе не меньше степени многочлена в знаменателе, и правильные, если степень многочлена в числителе меньше степени многочлена в знаменателе. В том же уроке говорилось о том, как представить неправильную дробь в виде суммы её целой части и некоторой правильной дроби.

На этом уроке будем учиться интегрировать такие рациональные функции, которые представлены в виде правильных дробей. Для этого существует метод неопределённых коэффициентов, основанный на теореме, которая гласит, что всякая правильная дробь может быть представлена в виде суммы простых дробей.

Приведённый ниже алгоритм интегирования рациональных функций будет пошагово проиллюстрирован в примерах.

Алгоритм интегрирования рациональных функций

Шаг 1. Определить вид многочлена в знаменателе дроби (он может иметь действительные, кратные действительные, комплексные и кратные комплексные корни) и в зависимости от вида разложить дробь на простые дроби, в числителях которых — неопределённые коэффициенты, число которых равно степени знаменателя.
Шаг 2. Определить значения неопределённых коэффициентов. Для этого потребуется решить систему уравнений, сводящуюся к системе линейных уравнений.
Шаг 3. Найти интеграл исходной рациональной функции (дроби) как сумму интегралов полученных простых дробей, к которым применяются табличные интегралы.

Переходим к первому шагу алгоритма

Видео:8.3 Интегрирование иррациональных функций.Скачать

Шаг 1: разложение исходной дроби

Многочлен в знаменателе имеет действительные корни. То есть, в знаменателе имеет место цепочка сомножителей вида , в которой каждый из сомножителей находится в первой степени. В этом случае разложение дроби с использованием метода неопределённых коэффициентов будет следующим:

Пример 1. Шаг 1. Дан интеграл от рациональной функции .

От нас требуется разложить подынтегральное выражение — правильную дробь на простые дроби.

Решение. Дискриминант уравнения положительный, поэтому многочлен в знаменателе имеет действительные корни. Получаем следующее разложение исходной дроби на сумму простых дробей:

Пример 2. Шаг 1.Дан интеграл от рациональной функции

Решение. Разложим знаменатель подынтегрального выражения на множители. Сначала можно вынести за скобки x. (На сайте есть урок о вынесении общего множителя за скобки.) Получаем следующую дробь:

Для разложения квадратного трёхчлена в скобках решаем квадратное уравнение:

Получаем разложение знаменателя на множители в подынтегральном выражении:

Дискриминант решённого выше квадратного уравнения положительный, то есть имеем дело со случаем, когда многочлен в знаменателе имеет действительные корни. Разложение исходной дроби подынтегрального выражения будет следующим:

Как и в первом примере, числа, обозначенные большими буквами, пока неизвестны. Отсюда и название — метод неопределённых коэффициентов.

Многочлен в знаменателе имеет кратные действительные корни. Этот случай имеет место, когда в цепочке сомножителей в знаменателе присутствует выражение вида , то есть один из многочленов в степени 2 и больше. В этом случае разложение дроби с использованием метода неопределённых коэффициентов будет следующим:

Пример 3. Шаг 1. Дан интеграл от рациональной функции .

Решение. Представляем разность квадратов в виде произведения суммы и разности .

Тогда подынтегральное выражение запишется в виде

все уравнения с многочленами которого имеют действительные корни. Это случай кратных действительных корней, так как последний сомножитель находится во второй степени. Получаем следующее разложение исходной дроби на простые дроби:

Как видим, в этом случае нужно понижать степень кратного многочлена с исходной до первой и записывать простую дробь с каждой из этих степеней в знаменатель.

Пример 4. Шаг 1. Дан интеграл от рациональной функции .

Решение. Уравнения с многочленами в знаменателе имеют действительные корни, а сами многочлены присутствуют в степенях больше первой. Поэтому получаем следующее разложение исходной дроби на простые дроби:

Многочлен в знаменателе имеет комплексные корни: дискриминант квадратного уравнения , присутствующего в цепочке сомножителей в знаменателе, меньше нуля. В этом случае при разложении дроби в простой дроби, соответствующей описанному выше сомножителю, в числителе нужно записывать линейное выражение с переменной x (это выражение — последнее в следующей записи):

Пример 5. Шаг 1. Дан интеграл от рациональной функции .

Решение. Уравнение в скобках имеет комплексные корни, а оба сомножителя присутствуют в знаменателе в первой степени. Поэтому получаем следующее разложение исходной дроби на простые дроби:

Пример 6. Шаг 1. Дан интеграл от рациональной функции .

Решение. Представим знаменатель дроби в подынтегральном выражении в виде следующего произведения сомножителей:

Решение. Уравнение с последним сомножителем имеет комплексные корни, а все сомножители присутствуют в знаменателе в первой степени. Поэтому получаем следующее разложение исходной дроби на простые дроби:

Многочлен в знаменателе имеет кратные комплексные корни: дискриминант квадратного уравнения , присутствующего в цепочке сомножителей в знаменателе, меньше нуля и этот сомножитель присутствует в степени 2 или больше. В этом случае разложение дроби с использованием метода неопределённых коэффициентов будет следующим:

То есть в сумме простых дробей число простых дробей с линейным выражением в числителе должно быть равно степени сомножителя, имеющего комплексные корни.

Пример 7. Шаг 1. Дан интеграл от рациональной функции .

Решение. Квадратный трёхчлен имеет комплексные корни и присутствует в знаменателе подынтегральной дроби во второй степени. Поэтому получаем следующее разложение дробного выражения:

Пример 8. Шаг 1. Дан интеграл от рациональной функции .

Решение. Квадратный трёхчлен в знаменателе имеет комплексные корни и присутствует в подынтегральной дроби во второй степени. Поэтому получаем следующее разложение дробного выражения:

Видео:Математика это не ИсламСкачать

Шаг 2: нахождение неопределённых коэффициентов

На первом шаге мы представили подынтегральные дроби в виде суммы дробей с неопределёнными коэффициентами. В начале этого шага потребуется привести полученную сумму дробей к общему знаменателю. После этого в их числителях будут произведения неопределённых коэффициентов на многочлены, которых нет в данной отдельной дроби, но которые есть в других полученных дробях.

Полученное таким образом выражение приравнивается к числителю исходной дроби. Затем составляется система из уравнений, в которых степени икса одинаковы. Путём решения системы и находятся неопределённые коэффициенты. Для решения достаточно знать, как системы уравнений решаются методом подстановки и методом сложения.

Пример 1. Шаг 2. На шаге 1 получили следующее разложение исходной дроби на сумму простых дробей с неопределёнными коэффициентами в числителях:

Умножаем неопределённые коэффициенты на многочлены, которых нет в данной отдельной дроби, но которые есть в других полученных дробях:

Раскрываем скобки и приравниваем полученое к полученному выражению числитель исходной подынтегральной дроби:

В обеих частях равенства отыскиваем слагаемые с одинаковыми степенями икса и составляем из них систему уравнений:

Сокращаем все иксы и получаем эквивалентную систему уравнений:

Решая систему, получаем следующие значения неопределённых коэффициентов:

Таким образом, окончательное разложение подынтегральной дроби на сумму простых дробей:

Пример 2. Шаг 2. На шаге 1 получили следующее разложение исходной дроби на сумму простых дробей с неопределёнными коэффициентами в числителях:

Теперь начинаем искать неопределённые коэффициенты. Для этого числитель исходной дроби в выражении функции приравниваем к числителю выражения, полученного после приведения суммы дробей к общему знаменателю:

Теперь требуется составить и решить систему уравнений. Для этого приравниваем коэффициенты при переменной в соответствующей степени в числителе исходного выражения функции и аналогичные коэффициенты в полученном на предыдущем шаге выражения:

Решаем полученную систему:

Итак, , отсюда получаем окончательное разложение подынтегральной дроби на сумму простых дробей:

Пример 3. Шаг 2. На шаге 1 получили следующее разложение исходной дроби на сумму простых дробей с неопределёнными коэффициентами в числителях:

Начинаем искать неопределённые коэффициенты. Для этого числитель исходной дроби в выражении функции приравниваем к числителю выражения, полученного после приведения суммы дробей к общему знаменателю:

Как и в предыдущих примерах составляем систему уравнений:

Сокращаем иксы и получаем эквивалентную систему уравнений:

Решая систему, получаем следующие значения неопределённых коэффициентов:

Получаем окончательное разложение подынтегральной дроби на сумму простых дробей:

Пример 4. Шаг 2. На шаге 1 получили следующее разложение исходной дроби на сумму простых дробей с неопределёнными коэффициентами в числителях:

Как приравнивать числитель исходной дроби к выражению в числителе, полученному после разложения дроби на сумму простых дробей и приведения этой суммы к общему знаменателю, мы уже знаем из предыдуших примеров. Поэтому лишь для контроля приведём получившуюся систему уравнений:

Решая систему, получаем следующие значения неопределённых коэффициентов:

Получаем окончательное разложение подынтегральной дроби на сумму простых дробей:

Пример 5. Шаг 2. На шаге 1 получили следующее разложение исходной дроби на сумму простых дробей с неопределёнными коэффициентами в числителях:

Самостоятельно приводим к общему знаменателю эту сумму, приравнивать числитель этого выражения к числителю исходной дроби. В результате должна получиться следующая система уравнений:

Решая систему, получаем следующие значения неопределённых коэффициентов:

Получаем окончательное разложение подынтегральной дроби на сумму простых дробей:

Пример 6. Шаг 2. На шаге 1 получили следующее разложение исходной дроби на сумму простых дробей с неопределёнными коэффициентами в числителях:

Производим с этой суммой те же действия, что и в предыдущих примерах. В результате должна получиться следующая система уравнений:

Решая систему, получаем следующие значения неопределённых коэффициентов:

Получаем окончательное разложение подынтегральной дроби на сумму простых дробей:

Пример 7. Шаг 2. На шаге 1 получили следующее разложение исходной дроби на сумму простых дробей с неопределёнными коэффициентами в числителях:

После известных действий с полученной суммой должна получиться следующая система уравнений:

Решая систему, получаем следующие значения неопределённых коэффициентов:

Получаем окончательное разложение подынтегральной дроби на сумму простых дробей:

Пример 8. Шаг 2. На шаге 1 получили следующее разложение исходной дроби на сумму простых дробей с неопределёнными коэффициентами в числителях:

Внесём некоторые изменения в уже доведённые до автоматизма действия для получения системы уравнений. Есть искусственный приём, который в некоторых случаях помогает избежать лишних вычислений. Приводя сумму дробей к общему знаменателю получаем и приравнивая числитель этого выражения к числителю исходной дроби, получаем:

Можно заметить, что если принять за значение икса единицу, то второе и третье слагаемые в правой части равенства обратятся в нули и нет необходимости их вычислять. Тогда получаем, что . Далее по уже отработанной схеме получаем систему уравнений:

Решая систему, получаем следующие значения неопределённых коэффициентов:

Получаем окончательное разложение подынтегральной дроби на сумму простых дробей:

Видео:6.2 Интегрирование рациональных функций. Часть 1Скачать

Шаг 3: нахождение интеграла исходной функции (дроби)

Полученные простые дроби и интегировать проще. К исходной сумме дробей применяется правило интеграла суммы (интеграл суммы равен сумме интегралов) и табличные интегралы. Чаще всего требуется применять табличные интегралы, приводящие к натуральному логарифму и арктангенсу.

Пример 1. Шаг 3. На шаге 2 получили окончательное разложение подынтегральной дроби на сумму простых дробей:

Интегрируем изначальную рациональную функцию как сумму дробей и используем табличный интеграл 10, приводящий к натуральному логарифму:

Последнее действие с натуральным логарифмом — приведение к единому выражению под логарифмом — может требоваться при выполнении работ, но требуется не всегда.

Пример 2. Шаг 3. На шаге 2 получили окончательное разложение подынтегральной дроби на сумму простых дробей:

Вновь применяем табличный интеграл, приводящий к натуральному логарифму:

Пример 3. Шаг 3. На шаге 2 получили окончательное разложение подынтегральной дроби на сумму простых дробей:

В результате интегрирования получаем сумму натуральных логарифмов и одной простой дроби, на случай, если требуется преобразование к единому логарифму, делаем и это:

Пример 4. Шаг 3. На шаге 2 получили окончательное разложение подынтегральной дроби на сумму простых дробей:

В результате интегрирования получаем сумму натуральных логарифмов и одной дроби, на случай, если требуется преобразование к единому логарифму, делаем и это:

Пример 5. Шаг 3. На шаге 2 получили окончательное разложение подынтегральной дроби на сумму простых дробей:

Интегрируем и получаем сумму натурального логарифма и арктангенса:

Пример 6. Шаг 3. На шаге 2 получили окончательное разложение подынтегральной дроби на сумму простых дробей:

Опять получаем сумму натурального логарифма и арктангенса:

Пример 7. Шаг 3. На шаге 2 получили окончательное разложение подынтегральной дроби на сумму простых дробей:

Интегрируя, получаем натуральные логарифмы и дробь:

Приведение к единому логарифму попробуйте выполнить самостоятельно.

Пример 8. Шаг 3. На шаге 2 получили окончательное разложение подынтегральной дроби на сумму простых дробей:

Интегрируя, получаем сумму натурального логарифма, арктангенса и дроби:

Видео:Неполные квадратные уравнения. Алгебра, 8 классСкачать

Примеры интегрирования рациональных функций (дробей)

Здесь мы приводим подробные решения трех примеров интегрирования следующих рациональных дробей:
, , .

Видео:Интегралы №7 Интегрирование рациональных алгебраических функций (Метод неопределенных коэффициентов)Скачать

Пример 1

Здесь под знаком интеграла стоит рациональная функция, поскольку подынтегральное выражение является дробью из многочленов. Степень многочлена знаменателя ( 3 ) меньше степени многочлена числителя ( 4 ). Поэтому, вначале необходимо выделить целую часть дроби.

1. Выделим целую часть дроби. Делим x 4 на x 3 – 6 x 2 + 11 x – 6 :

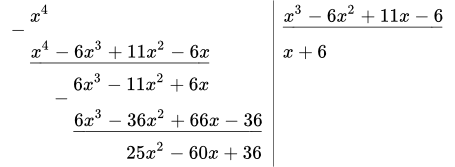
Отсюда
.

2. Разложим знаменатель дроби на множители. Для этого нужно решить кубическое уравнение:
.
Предположим, что оно имеет хотя бы один целый корень. Тогда он является делителем числа 6 (члена без x ). То есть целый корень может быть одним из чисел:
1, 2, 3, 6, –1, –2, –3, –6 .
Подставим x = 1 :
.

Итак, мы нашли один корень x = 1 . Делим на x – 1 :

Отсюда
.
Решаем квадратное уравнение .
.
Корни уравнения: , .
Тогда
.

3. Разложим дробь на простейшие.

Итак, мы нашли:
.
Интегрируем.

Видео:Неопределенный интеграл от иррациональной функции: 2 способа решения.Скачать

Пример 2

Здесь в числителе дроби – многочлен нулевой степени ( 1 = x 0 ). В знаменателе – многочлен третьей степени. Поскольку 0 , то дробь правильная. Разложим ее на простейшие дроби.

1. Разложим знаменатель дроби на множители. Для этого нужно решить уравнение третьей степени:
.
Предположим, что оно имеет хотя бы один целый корень. Тогда он является делителем числа 3 (члена без x ). То есть целый корень может быть одним из чисел:
1, 3, –1, –3 .
Подставим x = 1 :
.

Итак, мы нашли один корень x = 1 . Делим x 3 + 2 x – 3 на x – 1 :

Итак,
.

Решаем квадратное уравнение:
x 2 + x + 3 = 0 .
Находим дискриминант: D = 1 2 – 4·3 = –11 . Поскольку D 0 , то уравнение не имеет действительных корней. Таким образом, мы получили разложение знаменателя на множители:
.

2. Разложим дробь на простейшие. Ищем разложение в виде:
.
Освобождаемся от знаменателя дроби, умножаем на ( x – 1)( x 2 + x + 3) :
(2.1) .
Подставим x = 1 . Тогда x – 1 = 0 ,
.

Подставим в (2.1) x = 0 :
1 = 3 A – C ;
.

Приравняем в (2.1) коэффициенты при x 2 :
;
0 = A + B ;
.

Итак, мы нашли разложение на простейшие дроби:
.

3. Интегрируем.
(2.2) .
Для вычисления второго интеграла, выделим в числителе производную знаменателя и приведем знаменатель к сумме квадратов.

Вычисляем I ₂ .

.
Поскольку уравнение x 2 + x + 3 = 0 не имеет действительных корней, то x 2 + x + 3 > 0 . Поэтому знак модуля можно опустить.

Видео:6. Интегрирование рациональных функций / интегрирование рациональных дробей #1Скачать

Пример 3

Здесь под знаком интеграла стоит дробь из многочленов. Поэтому подынтегральное выражение является рациональной функцией. Степень многочлена в числителе равна 3 . Степень многочлена знаменателя дроби равна 4 . Поскольку 3 , то дробь правильная. Поэтому ее можно раскладывать на простейшие дроби. Но для этого нужно разложить знаменатель на множители.

1. Разложим знаменатель дроби на множители. Для этого нужно решить уравнение четвертой степени:
.
Предположим, что оно имеет хотя бы один целый корень. Тогда он является делителем числа 2 (члена без x ). То есть целый корень может быть одним из чисел:
1, 2, –1, –2 .
Подставим x = –1 :
.

Итак, мы нашли один корень x = –1 . Делим на x – (–1) = x + 1 :

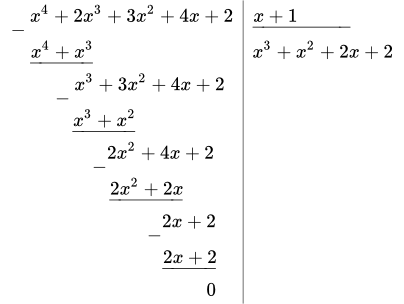
Итак,
.

Теперь нужно решить уравнение третьей степени:
.
Если предположить, что это уравнение имеет целый корень, то он является делителем числа 2 (члена без x ). То есть целый корень может быть одним из чисел:
1, 2, –1, –2 .
Подставим x = –1 :
.

Итак, мы нашли еще один корень x = –1 . Можно было бы, как и в предыдущем случае, разделить многочлен на , но мы сгруппируем члены:
.

Поскольку уравнение x 2 + 2 = 0 не имеет действительных корней, то мы получили разложение знаменателя на множители:
.

2. Разложим дробь на простейшие. Ищем разложение в виде:
.
Освобождаемся от знаменателя дроби, умножаем на ( x + 1) 2 ( x 2 + 2) :
(3.1) .
Подставим x = –1 . Тогда x + 1 = 0 ,
.

Продифференцируем (3.1):

;

.
Подставим x = –1 и учтем, что x + 1 = 0 :
;
; .

Подставим в (3.1) x = 0 :
0 = 2 A + 2 B + D ;
.

Приравняем в (3.1) коэффициенты при x 3 :
;
1 = B + C ;
.

Итак, мы нашли разложение на простейшие дроби:
.

Автор: Олег Одинцов . Опубликовано: 10-05-2015