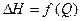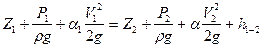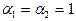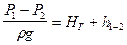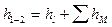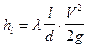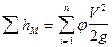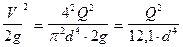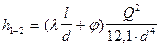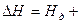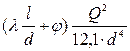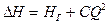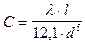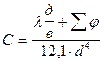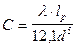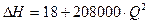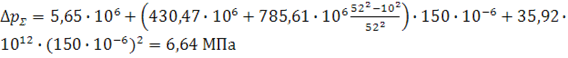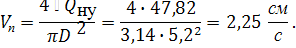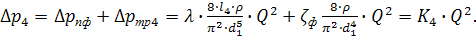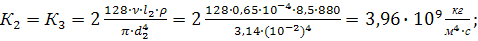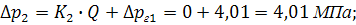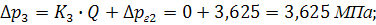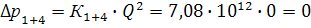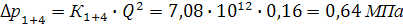Характеристика трубопровода ее уравнение и построение (4 видео)

Вывод уравнения гидравлической характеристики трубопровода.

При гидравлическом расчете трубопроводов весьма широко используется гидравлические методы расчета. Применение этого метода значительно облегчает и улучшает решение некоторых сложных задач, а в отдельных случаях (например, при исследовании совместной работы некоторых центробежных насосов на один общий трубопровод) является практически единственно возможным приемом, позволяющим получать искомое решение.

Гидравлической характеристикой трубопровода называется графическая зависимость напора, необходимого для перемещения жидкости по трубопроводу, от заданного расхода, т.е.

Для построения графической характеристики трубопровода необходимо знать уравнение, которым выражается интересующая нас зависимость.

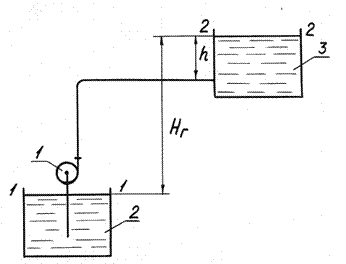Характеристика трубопровода ее уравнение и построение

Рассмотрим схему насосной установки, подающей жидкость из одного резервуара в другой (рисунок. 1).

На рисунке представлена производная схема трубопровода, соединяющего приемный резервуар (2) с напорным резервуаром (3). Из рисунка видно, что напор, созданный в начальном сечении трубопровода насосом (1), затрачивается на:

— сообщение жидкости геометрического напора путем поднятия её с приемного резервуара в напорный;

— создание скоростного напора;

— преодоление гидравлических сопротивлений трубопровода;

— поддержание избыточного давления в конечном сечении трубопровода, которое необходимо для преодоления гидростатического давления в напорном резервуаре на уровень конечного сечения.

Величина гидростатического давления в напорном резервуаре определяется расстоянием h от оси трубопровода, входящего в резервуар 3, и равна

P_K = 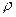gh

где P_K — величина давления в конечном сечении трубопровода.

Для вывода уравнение, характеризующего зависимость

воспользуемся уравнением Бернулли для реальной жидкости и применим его к схеме насосной установки (рисунок 1).

Выберем два сечения, проходящих по свободной поверхности жидкости в резервуарах 2 и 3 (сечения 1-1 и 2-2). За плоскость отсчета принимаем свободную поверхность жидкости в резервуаре 2.

Для выбранных двух сечений напишем уравнение Бернулли

Проанализируем члены уравнения Бернулли:

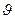
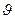
z₁=0 ; z₂=Н_Г; ₁= ₂ — т.к. при одинаковых диаметрах скорости также одинаковы.

Тогда уравнение Бернулли примет вид

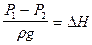
где 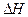— разность напоров в начальном и конечном сечениях.

Потери напора между сечениями 1-1 и 2-2 складывается из суммы напора по длине трубопровода и суммы потерь напора на местные сопротивления:

Потер напора по длине трубопровода определяются по формуле Дарси-Вейсбаха

Потери напора на местные сопротивления определяются из выражения :

Тогда общие потери будут равны

(1) В полученном уравнение (1) выразим скорость через расход:

;

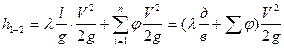
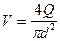
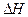
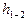
С учетом принятых значений и уравнение Бернулли будет иметь вид

Обозначим ,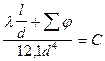

где 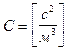— характеристический коэффициент трубопровода (иначе называется сопротивлением трубопровода).

Характеристический коэффициент определяется длиной трубопровода, его диаметром, шероховатостью, местными сопротивлениями и для данного трубопровода является постоянной величиной.

Окончательное уравнение гидравлической характеристики трубопровода имеет вид

Для полевых магистральных трубопроводов потеря напора на местные сопротивления по сравнению с потерями по длине трубопровода являются незначительными и при гидравлических расчетах ПМТ ими пренебрегают. С учетом этого характеристический коэффициент для ПМТ имеет вид

По виду уравнение

можно заключить, что гидравлическая характеристика трубопровода представляет собой параболу, симметричную относительно вертикальной оси, направленную выпуклостью вниз с вершиной, смещенной относительно начала координат на величину Н_Г.

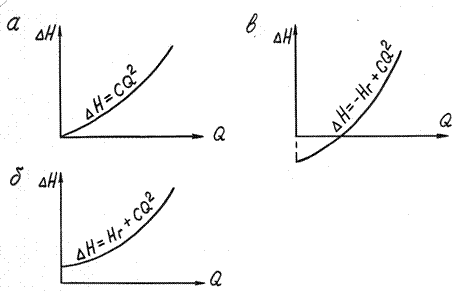
Если конечное сечение трубопровода размещено на одном уровне с начальным сечением трубопровода относительно плоскости отсчета (т.е. Z₂-Z₁=0), тогда геометрическая высота Н_Г равна нулю, а вершина параболы совпадает с началом осей координат (рисунок 2а).

Если конечное сечение трубопровода расположено выше начального сечения, тогда геометрическая высота Н_Г будет иметь знак плюс и вершина параболы будет лежать выше начала координат на величину Z₂-Z₁ (рисунок 2б).

Если конечное сечение трубопровода лежит ниже начального сечения трубопровода, тогда геометрическая высота Н_Г будет иметь знак минус и вершина параболы будет лежать ниже начала координат на величину Z₂-Z₁ (рисунок 2в).

Гидравлическая характеристика трубопровода может выражаться одним из трех графиков (рисунок 2 а,б,в.)

Вывод по первому вопросу

Полученное уравнение гидравлической характеристики может быть использовано при решении задач по определению режимов работы насосных агрегатов на трубопровод.

2. Методика построения гидравлической характеристики трубопровода.

Чтобы построить график гидравлической характеристики трубопровода необходимо выдержать следующую последовательность.

1. Вычислить характеристический коэффициент “С” и составить уравнение.

Характеристический коэффициент определяют по формуле:

Если вместо коэффициентов местных сопротивлений дана эквивалентная длина местных сопротивлений, то в уравнение подставляется расчетная длина трубопровода l_p , которая равна

где l — фактическая длина трубопровода;

l_э — эквивалентная длина местных сопротивлений.

Тогда уравнение для определения характеристического коэффициента трубопровода примет вид

При составлении расчетного уравнения

в него подставляются значение Нг и определено по уравнению значение С.

2. Задаться расходом жидкости Q и вычислить для каждого заданного значения расхода Q значение 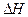. При этом могут быть два случая:

а) расход жидкости не задан. Тогда задаются произвольным значением расхода по арифметической прогрессии, начиная с нуля, с одной и той же разностью;

б)расход жидкости задан. Тогда заданный расход необходимо взять в “вилку” расходов, начиная с нуля.

3. Построить гидравлическую характеристику трубопровода.

Для этого выбирают два масштаба — горизонтальный по оси расхода в м 2 /с и вертикальный для разности напоров в метрах. Нанести точки и соединить их плавной кривой.

Методику построения гидравлических характеристик трубопровода рассмотрим на примере практического решения задачи.

ЗАДАЧА.

Построить гидравлическую характеристику трубопровода, подающего автобензин, если :

— длина трубопровода l=6000 м

— диаметр d=150 мм

— геометрическая высота Н_г=18 м

— коэффициент Дарси 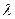=003

— эквивалентная длина местных сопротивлений l_э=4% от l

1. Вычислим характеристический коэффициент С и составим расчетное уравнение

l_p = l + l_э=6000 + 240 = 6240 м

с 2 /м 5

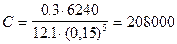
Расчетное уравнение будет иметь вид

2. Задаемся расходом и вычисляем

Q м 3 /с	0.004	0.008	0.012	0.016	0.02
H м

При Q₂=0/004 H₂= 18+208000*(0.004) 2 = 21 м и т.д.

— горизонтальный — в 1 см — 0.004 м 3 /с

— вертикальный — в 1 см — 10 м

3. Строим гидравлическую характеристику трубопровода (рисунок 3).

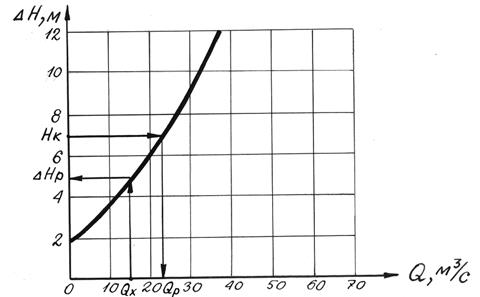По построенной характеристике мы можем для данного трубопровода решать следующие задачи без вычислений :

— определять необходимый напор для перекачки горючего с заданной производительностью;

— определять производительность трубопровода при заданном напоре.

Вывод по второму вопросу.

Рассмотренная методика облегчает процесс построения гидравлических характеристик простых трубопроводов.

3.Принцип построения гидравлических характеристик сложных трубопроводов.

В зависимости от конфигурации трубопроводы делятся на простые и сложные.

Простым трубопроводом называется трубопровод не имеющий разветвлений на пути движения жидкости от точки забора до точки потребления. Примером такого трубопровода может быть ПМТ, развернутый от фронтового склада до его отделения.

Сложным трубопроводом называется трубопровод, который представляет собой сеть труб, состоящую из основной магистральной линии и ряда отходящих от нее ответвлений.

Сложные трубопроводы делятся на следующие основные виды: последовательное соединение, параллельное соединение, разветвленные трубопроводы и др.

Рассмотренная во втором вопросе лекции методика построения гидравлической характеристики относится к простому трубопроводу. Построение гидравлической характеристики сложного трубопровода имеет ряд особенностей.

Рассмотрим принцип построения гидравлических характеристик для некоторых сложных трубопроводов.

а) Последовательное соединение трубопроводов

Схему последовательного соединения трубопроводов можно представить так :

d₁ d ₂

Расход жидкости в любом сечении трубопровода, исходя из уравнения неразрывности потока будет одинаковым, т.е.

а общие потери напора будут равны сумме потерь напора на отдельных участках

Для построения гидравлической характеристики такого трубопровода необходимо построить гидравлические характеристики каждого участка трубопровода отдельно (по методике построения гидравлической характеристики для простого трубопровода), а затем построить суммарную гидравлическую характеристику для всей линии трубопровода.

На рисунке 5 построены характеристики участков последовательного включения трубопроводов: кривая I представляет собой характеристику участка 1, крива II — участка 2.

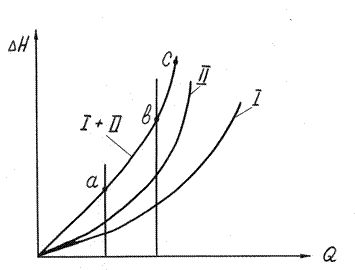Дальнейшее построение суммарной характеристики ведут следующим порядком. Так как при последовательном соединении потери напора суммируются, то кривые I и II сложим по вертикали. Для этого проведем ряд прямых параллельных оси ординат, каждая из которых пересечет обе кривые, сложим ординаты точек этих прямых с кривыми

В результата получим ряд точек а, б, с принадлежащих новой кривой I+II. Соединив эти точки плавной кривой, получим искомую суммарную характеристику всего рассматриваемого трубопровода, кривая I+II (рисунок 5).

б) Параллельное соединение трубопроводов

При параллельном соединении трубопроводов (рисунок 3, участки 2, 3, 4) построение характеристики этого сложного трубопровода следует начинать с построения

1 3 5

гидравлических характеристик отдельных параллельно включенных участков трубопровода по известной методике.

На рисунке 4 кривые II, III, IV представляют собой такие характеристики участков 2, 3 и 4.

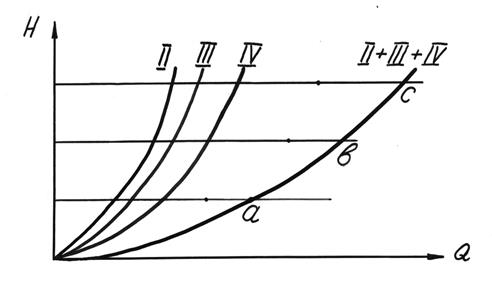Рисунок 7

При параллельном соединении трубопроводов жидкость, подходя с определенным расходом к точке их разветвления, проходит по разветвлениям и далее снова сливается в точке соединения этих трубопроводов. При этом общий расход определяется как сумма расходов в отдельных параллельно включенных участках, т.е.

Потери же напора в этих участках одинаковы, и полная потеря напора определяется как потеря в одном из них, т.е.

Поэтому для полстроения суммарной характеристики необходимо провести ряд горизонтальных прямых, параллельных оси абсцисс, и сложить при постоянных ординатах абсциссы точек их пересечения с характеристиками отдельных участков. В результате получим ряд точек а, б, с, определяющих суммарную характеристику II+III+IV трубопровода при параллельном включении

Разветвленный трубопровод можно представить в виде схемы (рисунок 5)

Если длина и диаметр каждого из участков трубопровода, известен коэффициент гидравлического сопротивления, то можно построить гидравлическую характеристику каждого из этих участков.

По известной методике построим гидравлические характеристики каждого участка трубопровода (1, 2 и 3) в отдельности (рисунок 8).

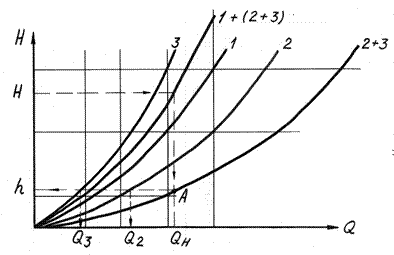Решение разветвленной системы трубопровода начнем со второго и третьего участков, которые соединены параллельно.

Заменим участки 2 и 3 эквивалентным трубопроводом (2+3), т.е. сложим гидравлические характеристики участков трубопровода 2 и 3 по оси расходов. После чего получим два участка трубопровода, соединенных последовательно (рисунок 9 ).

Далее строим суммарную характеристику двух последовательно соединенных трубопроводов 1+(2+3). Таким образом, мы получили суммарную характеристику развернутой сети трубопровода 1 + 2 + 3 ( рисунок 9).

о суммарной характеристике разветвленного трубопровода можно решать следующие задачи :

— задать напор Н, определить расход при этом напоре. Для решения этой задачи необходимо на оси ординат найти напор Н, и двигаясь от этой точки слева направо дойти до характеристики 1+(2+30, и опустив перпендикуляр на ось абсцисс получим искомый расход (Q_H) (рисунок 6).

— чтобы определить расход отдельно по трубопроводам 2 и 3 необходимо от Q_H восстановить перпендикуляр до пересечения с характеристикой (2+3), точка пересечения А (Рис. 6) дает напор, который одинаков для обеих участков 2 и 3 (рисунок 7 ). Двигаясь от точки А справа налево до точек пересечения с характеристиками 2 и 3 и, опускаясь по перпендикуляру от этих точек, найдем расходы Q₂ и Q₃.

Вывод по третьему вопросу

Рассмотренные способы построения суммарной гидравлической характеристики сложных трубопроводов имеет важное прикладное значение для специалистов службы горючего.

Заключение .

В лекции дано определение гидравлической характеристики трубопровода. выведено уравнение гидравлической характеристики простого трубопровода и на конкретном примере рассмотрена методика построения гидравлической характеристики простого трубопровода. изложен принцип построения гидравлической характеристики сложных трубопроводов.

Умение рассчитывать и строить гидравлическую характеристику трубопровода позволит офицеру службы горючего грамотно принимать решение при эксплуатации перекачивающих средств и трубопроводов.

\|	следующая лекция ==>
Расчет статически неопределимых плоско-пространственных рам методом сил	\|	Морфологический критерий

Дата добавления: 2016-11-29 ; просмотров: 5725 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Видео:Закон БернуллиСкачать

Характеристика трубопровода ее уравнение и построение

При расчетах напорных трубопроводов основной задачей является либо определение пропускной способности (расхода), либо потери напора на том или ином участке, равно как и на всей длине, либо диаметра трубопровода на заданных расходе и потерях напора.

В практике трубопроводы делятся на короткие и длинные. К первым относятся все трубопроводы, в которых местные потери напора превышают 5…10% потерь напора по длине. При расчетах таких трубопроводов обязательно учитывают потери напора в местных сопротивлениях. К ним относят, к примеру, маслопроводы объемных передач.

Ко вторым относятся трубопроводы, в которых местные потери меньше 5…10% потерь напора по длине. Их расчет ведется без учета местных потерь. К таким трубопроводам относятся, например, магистральные водоводы, нефтепроводы.

Учитывая гидравлическую схему работы длинных трубопроводов, их можно разделить также на простые исложные. Простыми называются последовательно соединенные трубопроводы одного или различных сечений, не имеющих никаких ответвлений. К сложным трубопроводам относятся системы труб с одним или несколькими ответвлениями, параллельными ветвями и т.д. К сложным относятся и так называемые кольцевые трубопроводы.

Жидкость по трубопроводу движется благодаря тому, что ее энергия в начале трубопровода больше, чем в конце. Этот перепад уровней энергии может создаваться несколькими способами: работой насоса, разностью уровней жидкости, давлением газа.

Рассмотрим простой трубопровод постоянного сечения, который расположен произвольно в пространстве (рис. 6.1), имеет общую длину l и диаметр d, а также содержит ряд местных сопротивлений (вентиль, фильтр и обратный клапан). В начальном сечении трубопровода 1-1 геометрическая высота равна z₁ и избыточное давление Р₁, а в конечном сечении 2-2 — соответственно z₂ и Р₂. Скорость потока в этих сечениях вследствие постоянства диаметра трубы одинакова и равна ν.

Запишем уравнение Бернулли для сечений 1-1 и 2-2. Поскольку скорость в обоих сечениях одинакова и α₁ = α₂, то скоростной напор можно не учитывать. При этом получим

Пьезометрическую высоту, стоящую в левой части уравнения, назовем потребным напором Н_потр. Если же эта пьезометрическая высота задана, то ее называют располагаемым напором Н_расп. Такой напор складывается из геометрической высоты H_потр, на которую поднимается жидкость, пьезометрической высоты в конце трубопровода и суммы всех потерь напора в трубопроводе.

Назовем сумму первых двух слагаемых статическим напором, который представим как некоторую эквивалентную геометрическую высоту

а последнее слагаемое Σh — как степенную функцию расхода

где K — величина, называемая сопротивлением трубопровода;
Q — расход жидкости;
m — показатель степени, который имеет разные значения в зависимости от режима течения.

Для ламинарного течения при замене местных сопротивлений эквивалентными длинами сопротивление трубопровода равно

Численные значения эквивалентных длин l_экв для различных местных сопротивлений обычно находят опытным путем.

Для турбулентного течения, используя формулу Вейсбаха-Дарси, и выражая в ней скорость через расход, получаем

По этим формулам можно построить кривую потребного напора в зависимости от расхода. Чем больше расход Q, который необходимо обеспечить в трубопроводе, тем больше требуется потребный напор Н_потр. При ламинарном течении эта кривая изображается прямой линией (рис.6.2, а), при турбулентном — параболой с показателем степени равном двум (рис.6.2, б).

Крутизна кривых потребного напора зависит от сопротивления трубопровода K и возрастает с увеличением длины трубопровода и уменьшением диаметра, а также с увеличением местных гидравлических сопротивлений.

Величина статического напора Н_ст положительна в том случае, когда жидкость движется вверх или в полость с повышенным давлением, и отрицательна при опускании жидкости или движении в полость с пониженным давлением. Точка пересечения кривой потребного напора с осью абсцисс (точка А) определяет расход при движении жидкости самотеком. Потребный напор в этом случае равен нулю.

Иногда вместо кривых потребного напора удобнее пользоваться характеристиками трубопровода.Характеристикой трубопровода называется зависимость суммарной потери напора (или давления) в трубопроводе от расхода:

Простые трубопроводы могут соединяться между собой, при этом их соединение может бытьпоследовательным или параллельным.

Последовательное соединение. Возьмем несколько труб различной длины, разного диаметра и содержащих разные местные сопротивления, и соединим их последовательно (рис. 6.3, а).

При подаче жидкости по такому составному трубопроводу от точки М к точке N расход жидкости Q во всех последовательно соединенных трубах 1, 2 и 3 будет одинаков, а полная потеря напора между точками М и Nравна сумме потерь напора во всех последовательно соединенных трубах. Таким образом, для последовательного соединения имеем следующие основные уравнения:

Эти уравнения определяют правила построения характеристик последовательного соединения труб (рис. 6.3, б). Если известны характеристики каждого трубопровода, то по ним можно построить характеристику всего последовательного соединения M-N. Для этого нужно сложить ординаты всех трех кривых.

Параллельное соединение. Такое соединение показано на рис. 6.4, а. Трубопроводы 1, 2 и 3 расположены горизонтально.

Обозначим полные напоры в точках М и N соответственно H_M и H_N , расход в основной магистрали (т.е. до разветвления и после слияния) — через Q, а в параллельных трубопроводах через Q₁, Q₂ и Q₃; суммарные потери в этих трубопроводах через Σ₁ , Σ₂ и Σ₃.

Очевидно, что расход жидкости в основной магистрали

Выразим потери напора в каждом из трубопроводов через полные напоры в точках М и N :

Отсюда делаем вывод, что

т.е. потери напора в параллельных трубопроводах равны между собой. Их можно выразить в общем виде через соответствующие расходы следующим образом

где K и m — определяются в зависимости от режима течения.

Из двух последних уравнений вытекает следующее правило: для построения характеристики параллельного соединения нескольких трубопроводов следует сложить абсциссы (расходы) характеристик этих трубопроводов при одинаковых ординатах ( Σ h). Пример такого построения дан на рис. 6.3, б.

Разветвленное соединение. Разветвленным соединением называется совокупность нескольких простых трубопроводов, имеющих одно общее сечение — место разветвления (или смыкания) труб.

Пусть основной трубопровод имеет разветвление в сечении М-М, от которого отходят, например, три трубы1, 2 и 3 разных диаметров, содержащие различные местные сопротивления (рис. 6.5, а). Геометрические высоты z₁, z₂ и z₃ конечных сечений и давления P₁, P₂ и P₃ в них будут также различны.

Так же как и для параллельных трубопроводов, общий расход в основном трубопроводе будет равен сумме расходов в каждом трубопроводе:

Записав уравнение Бернулли для сечения М-М и конечного сечения, например первого трубопровода, получим (пренебрегая разностью скоростных высот)

Обозначив сумму первых двух членов через H_ст и выражая третий член через расход (как это делалось в п.6.1), получаем

Аналогично для двух других трубопроводов можно записать

Таким образом, получаем систему четырех уравнений с четырьмя неизвестными: Q₁, Q₂ и Q₃ и H_M.

Построение кривой потребного напора для разветвленного трубопровода выполняется сложением кривых потребных напоров для ветвей по правилу сложения характеристик параллельных трубопроводов (рис. 6.5, б) — сложением абсцисс (Q) при одинаковых ординатах (H_M). Кривые потребных напоров для ветвей отмечены цифрами 1, 2 и 3 , а суммарная кривая потребного напора для всего разветвления обозначена буквами ABCD. Из графика видно, что условием подачи жидкости во все ветви является неравенство H_M > H_ст1.

Сложный трубопровод в общем случае составлен из простых трубопроводов с последовательным и параллельным их соединением (рис. 6.6, а) или с разветвлениями (рис. 6.6, б).

Рассмотрим разомкнутый сложный трубопровод (рис. 6.6, б). магистральный трубопровод разветвляется в точках А и С. Жидкость подается к точкам (сечениям) B, D и E с расходами Q _B и Q_D и Q_E .

Пусть известны размеры магистралей и всех ветвей (простых трубопроводов), заданы все местные сопротивления, а также геометрические высоты конечных точек, отсчитываемые от плоскости M — N и избыточные давления в конечных точках P_B и P_D и P_E.

Для этого случая возможны два вида задач:

Задача 1. Дан расход Q в основной магистрали M_A. Необходимо определить расходы Q_B и Q_D и Q_E, а также потребный напор в точке М.

Задача 2. Дан напор в точке М. Определить расход в магистрали Q и расходы в каждой ветви.

Обе задачи решают на основе одной и той же системы уравнений, число которых на единицу больше числа конечных ветвей, а именно:

уравнение равенства потребных напоров для ветвей CD и CE

уравнение равенства потребных напоров для ветви АВ и сложного трубопровода АСЕD

выражение для потребного напора в точке М

Расчет сложных трубопроводов часто выполняют графоаналитическим способом, т.е. с применением кривых потребного напора и характеристик трубопроводов. Кривую потребного напора для сложного трубопровода следует строить следующим образом:
1) сложный трубопровод разбивают на ряд простых;
2) строят кривые потребных напоров для каждого из простых трубопроводов;
3) складывают кривые потребных напоров для ветвей (и параллельных линий, если они имеются) по правилу сложения характеристик параллельных трубопроводов;
4) полученную кривую складывают с характеристикой последовательно присоединенного трубопровода по соответствующему правилу (см. п.6.2).

Таким образом, при расчете идут от конечных точек трубопровода к начальной точке, т.е. против течения жидкости.

Сложный кольцевой трубопровод. Представляет собой систему смежных замкнутых контуров, с отбором жидкости в узловых точках или с непрерывной раздачей жидкости на отдельных участках (рис. 6.7).

Задачи для таких трубопроводов решают аналогичным методом с применением электроаналогий (закон Кирхгофа). При этом основываются на двух обязательных условиях. Первое условие — баланс расходов, т.е. равенство притока и оттока жидкости для каждой узловой точки. Второе условие — баланс напоров, т.е. равенство нулю алгебраической суммы потерь напора для каждого кольца (контура) при подсчете по направлению движения часовой стрелки или против нее.

Для расчета таких трубопроводов типичной является следующая задача. Дан максимальный напор в начальной точке, т.е. в точке 0, минимальный напор в наиболее удаленной точке Е, расходы во всех шести узлах и длины семи участков. Требуется определить диаметры трубопроводов на всех участках.

Как уже отмечалось выше, перепад уровней энергии, за счет которого жидкость течет по трубопроводу, может создаваться работой насоса, что широко применяется в машиностроении. Рассмотрим совместную работу трубопровода с насосом и принцип расчета трубопровода с насосной подачей жидкости.

Трубопровод с насосной подачей жидкости может быть разомкнутым, т.е. по которому жидкость перекачивается из одной емкости в другую (рис. 6.8, а), или замкнутым (кольцевым), в котором циркулирует одно и то же количество жидкости (рис. 6.8, б).

Рассмотрим трубопровод, по которому перекачивают жидкость из нижнего резервуара с давлением P ₀ в другой резервуар с давлением P₃ (рис. 6.8, а). Высота расположения оси насоса H₁ называетсягеометрической высотой всасывания, а трубопровод, по которому жидкость поступает к насосу,всасывающим трубопроводом или линией всасывания. Высота расположения конечного сечения трубопровода H₂ называется геометрической высотой нагнетания, а трубопровод, по которому жидкость движется от насоса, напорным или линией нагнетания.

Составим уравнением Бернулли для потока рабочей жидкости во всасывающем трубопроводе, т.е. для сечений 0-0 и 1-1 (принимая α = 1):

Это уравнение является основным для расчета всасывающих трубопроводов.

Теперь рассмотрим напорный трубопровод, для которого запишем уравнение Бернулли, т.е. для сечений 2-2и 3-3:

Левая часть этого уравнения представляет собой энергию жидкости на выходе из насоса. А на входе насоса энергию жидкости можно будет аналогично выразить из уравнения:

Таким образом, можно подсчитать приращение энергии жидкости, проходящей через насос. Эта энергия сообщается жидкости насосом и поэтому обозначается обычно H_нас.

Для нахождения напора H_нас вычислим уравнение :

где Δz — полная геометрическая высота подъема жидкости, Δz = H ₁ + H₂;
КQ m — сумма гидравлических потерь,
P₃ и Р₀ — давление в верхней и нижней емкости соответственно.

Если к действительной разности уровней Δz добавить разность пьезометрических высот ( P₃ — Р₀ ) ( ρg ), то можно рассматривать увеличенную разность уровней

и формулу можно переписать так:

Из этой формулы делаем вывод, что

Отсюда вытекает следующее правило устойчивой работы насоса: при установившемся течении жидкости в трубопроводе насос развивает напор, равный потребному.

На этом равенстве основывается метод расчета трубопроводов с насосной подачей, который заключается в совместном построении в одном и том же масштабе и на одном графике двух кривых: напора H_потр = f₁(Q)и характеристики насоса H_нас = f₂(Q) и в нахождении их точки пересечения (рис. 6.9).

Характеристикой насоса называется зависимость напора, создаваемого насосом, от его подачи (расхода жидкости) при постоянной частоте вращения вала насоса. На рис. 6.9 дано два варианта графика: а — для турбулентного режима; б — для ламинарного режима. Точка пересечения кривой потребного напора с характеристикой насоса называется рабочей точкой. Чтобы получить другую рабочую точку, необходимо изменить открытие регулировочного крана (изменить характеристику трубопровода) или изменить частоту вращения вала насоса.

Гидравлическим ударом называется резкое повышение давления, возникающее в напорном трубопроводе при внезапном торможении потока рабочей жидкости. Этот процесс является очень быстротечным и характеризуется чередованием резких повышений и понижений давления, которое связано с упругими деформациями жидкости и стенок трубопровода. Гидравлический удар чаще всего возникает при резком открытии или закрытии крана или другого устройства, управляемого потоком.

Пусть в конце трубы, по которой движется жидкость со скоростью υ₀, произведено мгновенное закрытие крана (рис. 6.10, а).

При этом скорость частиц, натолкнувшихся на кран, будет погашена, а их кинетическая энергия перейдет в работу деформации стенок трубы и жидкости. При этом стенки трубы растягиваются, а жидкость сжимается в соответствии с увеличением давления на величину ΔP_уд, которое называется ударным. Область (сечение n — n), в которой происходит увеличение давления, называется ударной волной. Ударная волна распространяется вправо со скоростью c, называемой скоростью ударной волны.

Когда ударная волна переместится до резервуара, жидкость окажется остановленной и сжатой во всей трубе, а стенки трубы — растянутыми. Ударное повышение давления распространится на всю длину трубы (рис. 6.10, б).

Далее под действием перепада давления ΔP_уд частицы жидкости устремятся из трубы в резервуар, причем это течение начнется с сечения, непосредственно прилегающего к резервуару. Теперь сечение n-nперемещается обратно к крану с той же скоростью c, оставляя за собой выровненное давление P₀ (рис. 6.10, в).

Жидкость и стенки трубы предполагаются упругими, поэтому они возвращаются к прежнему состоянию, соответствующему давлению P₀. Работа деформации полностью переходит в кинетическую энергию, и жидкость в трубе приобретает первоначальную скорость υ₀, но направленную теперь в противоположную теперь сторону.

С этой скоростью весь объем жидкости стремится оторваться от крана, в результате возникает отрицательная ударная волна под давлением P₀ — ΔP_уд, которая направляется от крана к резервуару со скоростью c, оставляя за собой сжавшиеся стенки трубы и расширившуюся жидкость, что обусловлено снижением давления (рис. 6.10, д). Кинетическая энергия жидкости вновь переходит в работу деформаций, но противоположного знака.

Состояние трубы в момент прихода отрицательной ударной волны к резервуару показано на рис. 6.10, е. Так же как и для случая, изображенного на рис. 6.10, б, оно не является равновесным. На рис. 6.10, ж, показан процесс выравнивания давления в трубе и резервуаре, сопровождающийся возникновением движения жидкости со скоростью υ₀.

Очевидно, что как только отраженная от резервуара ударная волна под давлением ΔP _уд достигнет крана, возникнет ситуация, уже имевшая место в момент закрытия крана. Весь цикл гидравлического удара повторится.

Протекание гидравлического удара во времени иллюстрируется диаграммой, представленной на рис. 6.11, а и б.

Штриховыми линиями показано теоретическое изменение давления у крана в точке А, а сплошной действительный вид картины изменения давления по времени (рис. 6.11, а). При этом затухание колебаний давления происходит за счет потерь энергии жидкости на преодоление сил трения и ухода энергии в резервуар.

Повышение давления при гидравлическом ударе можно определить по формуле

Данное выражение носит название формулы Жуковского. В нем скорость распространения ударной волны c определится по формуле:

где r — радиус трубопровода;
E — модуль упругости материала трубы;
δ — толщина стенки трубопровода;
K — объемный модуль упругости (см. п.1.3)

Если предположить, что труба имеет абсолютно жесткие стенки, т.е. E = , то скорость ударной волны определится из выражения

Для воды эта скорость равна 1435 м/с, для бензина 1116 м/с, для масла 1200 — 1400 м/с.

При проектировании напорных трубопроводов следует учитывать, что их пропускная способность в период эксплуатации снижается (например, для водопроводных труб до 50% и даже ниже). Вследствие коррозии и образования отложений в трубах (инкрустации), шероховатость труб увеличивается. Это можно оценить по формуле:

где k₀ — абсолютная шероховатость для новых труб, (мм),
k_t — шероховатость через t лет эксплуатации,
α — коэффициент характеризующий быстроту возрастания шероховатости (мм/год).

Видео:Характеристика насосной системы. Потери по длине трубопровода.Скачать

Построение характеристики трубопровода и определение рабочей точки гидросистемы.

Подставив данные из условия задачи, получим:

Определяем значения 5 точек в рабочем диапазоне значений расходов для Q = 0:

для Q = 50·10 -6 м 3 /с:

для Q = 100·10 -6 м 3 /с:

для Q = 150·10 -6 м 3 /с:

для Q = 200·10 -6 м 3 /с:

Таблица 1. Результаты расчета характеристики трубопровода

Q (м 3 /с)	50×10 -6	100×10 -6	150×10 -6	200×10 -6
Δp_Σ (мПа)	5,65	5,8	6,13	6,64	7,33

По этим данным строится характеристика трубопровода (кривая 3). Точка пересечения линии 3 с CD дает рабочую точку гидросистемы (точка R). Ее координаты:

Q_ну = 47,82 см 3 /с; р_н = 5,79 МПа.

5. Определение искомых величин

Так как вся подача насосной установки Qну поступает в гидроцилиндр, то скорость движения его штока определяется по формуле (в соответствии с рекомендациями принимаем объемный КПД гидроцилиндра равным единице)

Мощность, потребляемая гидроприводом, равна мощности, потребляемой насосной установкой, и в данном случае определяется по формуле

Для определения КПД гидропривода ηгп вначале необходимо рассчитать полезную мощность, развиваемую на его выходном звене

N вых F Vп 12·10 3 ·0,0225 = 270 Вт

Гидропривод вращательного движения

Рис.1. Схема гидропривода вращательного движения

Дано:вес грузов G1 = 2,1 кН и G2 = 1,9 кН; параметры насоса: максимальный рабочий объем Wон = 30 см3, частота вращения валаnн=25об/с, объемный КПД ηон = 0,82 при давлении р’ = 6 МПа, механический КПД ηмн= 0,9; параметры регулятора подачи: давление настройки pр=4,85 МПа, Kр=0,001м3/(МПа·с); размеры гидролиний:d1 = d2 = 1 см, l1 = 3 м, l2 = l3 = 8,5м, l4 = 5 м; коэффициент сопротивленияфильтра ζф=3; параметры гидродросселя: площадь проходного сечения Sдр = 14 мм2, коэффициент расхода µдр = 0,7; параметры гидромоторов: рабочий объем Wг = 32 см3, механический КПД ηмг = 0,9, объемный КПДпринять ηог=0,99; передаточное число механического редуктора inвх /nвых=40, диаметр шкива D = 0,7 м; параметры рабочей жидкости: кинематическая вязкость ν = 0,65 см2/с, плотность ρ = 880 кг/м3. Принять, что в трубах с диаметром d1 режим течения турбулентный и λ = 0,04, а с диаметром d2 – ламинарный.

– скорости движения тросов грузов;

– мощность, потребляемую гидроприводом;

– коэффициент полезного действия гидропривода.

1) Замена принципиальной схемы гидропривода эквивалентной

На рис. 2 приведена эквивалентная, или расчетная, схема, полученная на основании принципиальной схемы гидропривода (см. рис. 1).

Из анализа расчетной схемы ясно, что рассматриваемый гидропривод представляет собой сложный трубопровод с последовательно-параллельным соединением отдельных участков. Его целесообразно разбить на 4 простых трубопровода: 1, 2, 3 и 4 (рис. 2).

Рис. 2. Эквивалентная схема

2) Построение характеристики насосной установки

Учитывая линейность характеристик насоса и насосной установки с регулятором подачи, построение каждой из них проводим по двум точкам в соответствии с вышеизложенной методикой.

Для насоса: первая точка А — при р = 0,

вторая точка В — при р’ = 6 МПа,

Q’ = Q_Tmax ·η_он =0,75·10 -3 ·0,82=0, 615· 10 -3 м 3 /с.

Соединяя точки А и В, получаем характеристику насоса (рис. 3).

Для насосной установки с регулятором подачи:

первая точка С — это точка пересечения горизонтали, соответствующей давлению настройки регулятора p_p = 4,85 МПа, с характеристикой насоса. Подача насосной установки при этом равна Q’_ну = 0,641·10 -3 м 3 /с;

вторая точка С’ — ее координаты определяются, зная Q’_ну и произвольно задаваясь давлением на выходе насоса, при p»_н=5,25 МПа,

Проведя прямую через точки С и С’ до пересечения с осью ординат в точке D, получаем характеристику насосной установки (ломаная линия АCD на рис. 3).

3) Составление уравнений характеристик простых трубопроводов

Составление уравнений характеристик простых трубопроводов 1, 2, 3 и 4 базируется на заданном условии: на участках 1 и 4 — режим течения турбулентный, а на участках 2 и 3 — ламинарный. Отсюда:

для 1:

для 2:

для 3:

ддя4:

В этих уравнениях значение моментов на валах гидромоторов М₁ и М₂ определяются с учетом передаточных отношений редукторов

4) Построение суммарной характеристики сложного трубопровода и определение рабочей точки гидросистемы

Заметим, что участки 1 и 4 включены последовательно, поэтому для них можно написать общее уравнение

и сразу построить их суммарную характеристику. Подставив данные из условия задачи, получим:

Поскольку характеристики 2 и 3 трубопроводов линейны, для их построения достаточно двух точек, а для построения нелинейной характеристики К₁₊₄ = f(Q) используем 6 точек. Результаты расчетов заносим в таблицу 1.

Для Q = 0,2 м 3 /с:

Для Q = 0,3 м 3 /с:

Для Q = 0,4 м 3 /с:

Для Q = 0,5 м 3 /с:

Для Q = 0,6 м 3 /с:

Таблица 1. Результаты расчета характеристик трубопровода

Q (м 3 /с)	0,2·10 -3	0,3·10 -3	0,4·10 -3	0,5·10 -3	0,6·10 -3
Δp₂ (МПа)	4,01	5,99
Δp₃ (МПа)	3,625	5,605
Δp₁₊₄ (МПа)	0,28	0,64	1,13	1,77	2,55

По данным таблицы на графике (см. рис. 3) строим характеристики каждого простого трубопровода (линии 1+4, 2 и 3).

Затем по правилам графического сложения характеристик параллельных участков (они складываются за счет суммирования отрезков вдоль оси расходов) получаем суммарную характеристику участков 2 и 3 (ломаная линия 2+3). Далее проводим графическое сложение полученной характеристики Δр₂₊₃ =f(Q) c характеристикой Δр₂₊₃ =f(Q).

Рис. 3. Графическое решение

Эти характеристики складываются по правилу сложения характеристик последовательно соединенных трубопроводов, т.е. за счет суммирования отрезков вдоль оси давлений. В результате получаем суммарную характеристику всего сложного трубопровода (линия Σ).

Пересечение полученной характеристики сложного трубопровода с характеристикой насосной установки определяет рабочую точку гидросистемы (точка R на рис.3). Ее координаты р_н = 5,17 МПа и Q_ну=0,319·10 -3 м 3 /с

5) Определение искомых величин

Определим потребляемую гидроприводом мощность, для этого через точку R проводим прямую параллельно АВ и определяем Q’_т = 0,436·10 -3 м 3 /с. Тогда

Чтобы определить скорости подъема грузов и КПД гидропривода, необходимо найти частоту вращения вала каждого гидромотора. Для этого необходимо знать величины расходов Q₂ и Q₃ в параллельных трубопроводах 2 и 3.

Эту задачу можно решить графически, исходя из того, что при наличии графической зависимости р = f(Q) по одной из известных координат легко определяется другая.

Опустив вертикаль из точки R, соответствующую подаче насосной установки Q_ну, находим точку R₁ пересечения этой вертикали с кривой 2+3 и, следовательно, потерю давления Δр₂₊₃ на участке параллельного соединения, где Δр₂₊₃ = Δр₂ = Δр₃.

Проведя теперь горизонталь через точку R₁, соответствующую потерям давления Δр₂ = Δр₃, находим точки ее пересечения с характеристиками 2-го и 3-го трубопроводов (соответственно, точки R₂ и R₃). Опустив вертикали из точек R₂ и R₃, находим расходы Q₂ = 0,111·10 -3 м 3 /с и Q₃ = 0,208·10 -3 м 3 /с.

По известным расходам Q₂ и Q₃ с учетом передаточного отношения i механического редуктора и диаметра D шкива определяем скорости подъема левого V₁ и правого V₂ грузов. При этом целесообразно использовать формулу