| Теплоёмкость идеального газа. Уравнение Майера |   |
Теплоёмкость тела характеризуется количеством теплоты, необходимой для нагревания этого тела на один градус:
Однако, теплоёмкость – величина неопределённая, поэтому пользуются понятиями удельной и молярной теплоёмкости. Удельная теплоёмкость (Суд) есть количество теплоты, необходимое для нагревания единицы массы вещества на 1 градус [Cуд] = Дж/К. Для газов удобно пользоваться молярной теплоемкостью Cμ— количество теплоты, необходимое для нагревания 1 моля газа на 1 градус:
Из п. 1.2 известно, что молярная масса – масса одного моля:
Теплоёмкость термодинамической системы зависит от того, как изменяется состояние системы при нагревании. Если газ нагревать при постоянном объёме, то всё подводимое тепло идёт на нагревание газа, то есть изменение его внутренней энергии. Теплоёмкость при этом обозначается СV. СР – теплоемкость при постоянном давлении. Если нагревать газ при постоянном давлении Р в сосуде с поршнем, то поршень поднимется на некоторую высоту h, то есть газ совершит работу (рис. 4.2). Итак, проводимое тепло и теплоёмкость зависят от того, каким путём осуществляется передача тепла. Значит, Q и С не являются функциями состояния. Величины СР и СV оказываются связанными простыми соотношениями. Найдём их. Пусть мы нагреваем один моль идеального газа при постоянном объёме(dA = 0). Тогда первое начало термодинамики запишем в виде:
Теплоемкость при постоянном объёме будет равна:
Из (4.2.4) следует, что
Для произвольной идеальной массы газа:
При изобарическом процессе, кроме увеличения внутренней энергии, происходит совершение работы газом:
Из этого следует, что физический смысл универсальной газовой постоянной в том, что R – численно равна работе, совершаемой одним молем газа при нагревании на один градус в изобарическом процессе. Используя это соотношение, Роберт Майер в 1842 г. вычислил механический эквивалент теплоты: 1 кал = 4,19 Дж. Полезно знать формулу Майера для удельных теплоёмкостей: Видео:Уравнение состояния идеального газа. 10 класс.Скачать  Первое начало термодинамики. Теплоемкость идеального газа. Уравнение МайераПервое начало термодинамики — один из трёх основных законов термодинамики, представляет собой закон сохранения энергии для термодинамических систем. Первое начало термодинамики было сформулировано в середине XIX века в результате работ немецкого учёного Ю. Р. Майера, английского физика Дж. П. Джоуля и немецкого физика Г. Гельмгольца [1] . Согласно первому началу термодинамики, термодинамическая система может совершать работу только за счёт своей внутренней энергии или каких-либо внешних источников энергии. Первое начало термодинамики часто формулируют как невозможность существования вечного двигателя первого рода, который совершал бы работу, не черпая энергию из какого-либо источника. Теплоёмкость тела характеризуется количеством теплоты, необходимой для нагревания этого тела на один градус:
Размерность теплоемкости: [C] = Дж/К. Однако, теплоёмкость – величина неопределённая, поэтому пользуются понятиями удельной и молярной теплоёмкости. Удельная теплоёмкость (Суд) есть количество теплоты, необходимое для нагревания единицы массы вещества на 1 градус [Cуд] = Дж/К. Для газов удобно пользоваться молярной теплоемкостью Cμ— количество теплоты, необходимое для нагревания 1 моля газа на 1 градус:
Из п. 1.2 известно, что молярная масса – масса одного моля:
где А – атомная масса; mед — атомная единица массы; NА — число Авогадро; моль μ – количество вещества, в котором содержится число молекул, равное числу атомов в 12 г изотопа углерода 12 С. Теплоёмкость термодинамической системы зависит от того, как изменяется состояние системы при нагревании. Если газ нагревать при постоянном объёме, то всё подводимое тепло идёт на нагревание газа, то есть изменение его внутренней энергии. Теплоёмкость при этом обозначается СV. СР – теплоемкость при постоянном давлении. Если нагревать газ при постоянном давлении Р в сосуде с поршнем, то поршень поднимется на некоторую высоту h, то есть газ совершит работу (рис. 4.2). Следовательно, проводимое тепло затрачивается и на нагревание и на совершение работы. Отсюда ясно, что Итак, проводимое тепло и теплоёмкость зависят от того, каким путём осуществляется передача тепла. Значит, Q и С не являются функциями состояния. Величины СР и СV оказываются связанными простыми соотношениями. Найдём их. Пусть мы нагреваем один моль идеального газа при постоянном объёме(dA = 0). Тогда первое начало термодинамики запишем в виде:
т.е. бесконечно малое приращение количества теплоты Теплоемкость при постоянном объёме будет равна:
так как U может зависеть не только от температуры. Но в случае идеального газа справедлива формула (4.2.4). Из (4.2.4) следует, что
Внутренняя энергия идеального газа является только функцией температуры (и не зависит от V, Р и тому подобных), поэтому формула (4.2.5) справедлива для любого процесса. Для произвольной идеальной массы газа:
При изобарическом процессе, кроме увеличения внутренней энергии, происходит совершение работы газом:
Из основного уравнения молекулярно-кинетической теории
Это уравнение Майера для одного моля газа. Из этого следует, что физический смысл универсальной газовой постоянной в том, что R – численно равна работе, совершаемой одним молем газа при нагревании на один градус в изобарическом процессе. Используя это соотношение, Роберт Майер в 1842 г. вычислил механический эквивалент теплоты: 1 кал = 4,19 Дж. Полезно знать формулу Майера для удельных теплоёмкостей:
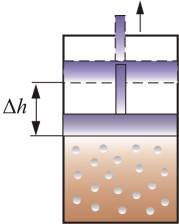
19. Адиабатический процесс. Адиабати́ческий, или адиаба́тный проце́сс (от др.-греч. ἀδιάβατος — «непроходимый») — термодинамический процесс в макроскопической системе, при котором система не обменивается теплотой с окружающим пространством. Адиабатический процесс является частным случаем политропного процесса, так как при нём теплоёмкость газа равна нулю и, следовательно, постоянна [2] . Адиабатические процессы обратимы только тогда, когда в каждый момент времени система остаётсяравновесной (например, изменение состояния происходит достаточно медленно) и изменения энтропии не происходит. Некоторые авторы (в частности, Л. Д. Ландау) называли адиабатическими только обратимые адиабатические процессы [3] . Обратимый адиабатический процесс для идеального газа описывается уравнением Пуассона. Если термодинамический процесс в общем случае представляет собой три процесса — теплообмен, совершение системой (или над системой) работы и изменение её внутренней энергии [5] , то адиабатический процесс в силу отсутствия теплообмена (
где Изменения энтропии S системы в обратимом адиабатическом процессе вследствие передачи тепла через границы системы не происходит [8] :
Здесь Работа газа[править | править вики-текст] Основная статья: Термодинамическая работа
Совершение над газом работы на элементарном участке dh. Совершаемая работа показана красными лампочками Поясним понятие работы применительно к адиабатическому процессу. В частном случае, когда работа совершается через изменение объёма, можно определить её следующим способом: пусть газ заключён в цилиндрический сосуд, плотно закрытый легко скользящим поршнем, если газ будет расширяться, то он будет перемещать поршень и при перемещении на отрезок
где F — сила, с которой газ действует на поршень. Перепишем уравнение:
где s — площадь поршня. Тогда работа будет равна [9] [10]
где Основное уравнение термодинамики примет вид [11] :
Это условие будет выполняться, если скорость хода поршня (протекания процесса в общем случае) будет удовлетворять определённым условиям. С одной стороны она должна быть достаточно малой, чтобы процесс можно было считать квазистатическим. Иначе при резком изменении хода поршня давление, которое его перемещает, будет отличаться от давления в целом по газу. То есть газ должен находиться в равновесии, без турбулентностей и неоднородностей давления и температуры. Для этого достаточно передвигать поршень со скоростью, существенно меньшей, чем скорость звука в данном газе. С другой стороны скорость должна быть достаточно большой, чтобы можно было пренебречь обменом тепла с окружающей средой и процесс оставался адиабатическим [12] [13] . Однако работа может совершаться и другими путями — например, идти на преодоление межмолекулярного притяжения газов. В этом случае параллельно с изменением внутренней энергии будет происходить процессы совершения нескольких работ разной физической природы, и основное уравнение термодинамики примет вид:
где Видео:Термодинамика | уравнение МайераСкачать  Запишите уравнение Майера. Укажите все входящие в него величиныОТЧЕТ О САМОСТОЯТЕЛЬНОЙ РАБОТЕ по дисциплине «Техническая термодинамика и теплопередача»
1. Охарактеризуйте область применения уравнения состояния идеального газа. Основные параметры газа (p, v, T) связаны между собой, что определяет уравнение состояния. Форма этого уравнения, удобная для расчетов, получается на основе законов идеального газа. Закон Бойля-Мариотта устанавливает связь между параметрами, если температура постоянна (Т = const): также справедливо соотношение: Закон Гей-Люссака применим, если постоянно давление (p = const):
При неизменном объеме (v = const) соотношение параметров определяется законом Шарля: После несложных математических преобразований можно получить:
Константу принято обозначать R и называть удельной газовой по-стоянной. Ее физический смысл – работа расширения 1 кг газа, нагреваемого при постоянном давлении на 1 К, размерность Дж/(кг К) или кДж/(кг К). Уравнение состояния для 1 кг газа (уравнение Клапейрона): pv = RT, для m кг газа: pV = mRT. Количество вещества – величина, определяемая числом структур-ных элементов (атомов, молекул, ионов и других частиц). Единицей в системе СИ является «моль» или киломоль, обозначается «кмоль». Масса киломоля – молярная масса, обозначается буквой М, изме-ряется в кг/кмоль; молярный объем (объем киломоля) Vm, м3/кмоль; чис-ло киломолей ν определяется по формуле: Уравнение состояния для 1 киломоля газа (уравнение Клапейрона-Менделеева): а для ν киломолей газа записывается так: pV = ν R0T, (2.12, а) где R0 – молярная (универсальная) газовая постоянная; R0 = 8314 Дж/(кмоль К). Формулы для определения удельной газовой постоянной R, удель-ного объема v0 и плотности газа ρ0 при нормальных физических услови-ях: Объем 22,4 м3 занимает 1 киломоль любого газа при нормальных физических условиях (следствие из закона Авогадро). Запишите уравнение Майера. Укажите все входящие в него величины. где Это уравнение показывает, что Ср больше, чем Сν на величину универсальной газовой постоянной R. Это объясняется тем, что при изобарном нагревании газа, в отличие от изохорного нагревания, требуется дополнительное количество теплоты на совершение работы расширения газа. Физический смысл универсальной газовой постоянной в том, что R – численно равна работе, совершаемой одним молем газа при нагревании на один градус в изобарическом процессе. Формула Майера для удельных теплоёмкостей:
3. Как изменяется внутренняя энергия, и какая совершается работа при подводе и отводе теплоты в политропных процессах III группы? 4. Какие допущения приняты при рассмотрении идеальных циклов двигателей внутреннего сгорания? При термодинамическом анализе циклов ДВС приняты следующие допущения, позволяющие идеализировать работу двигателей: — В качестве рабочего тела принимается идеальный газ, теплоемкость котopoгo не зависит от температуры; — Цикл замкнут, и на всех его стадиях качественный и количественный состав рабочего тела остается неизменным; — Теплота к рабочему телу подводится от внешнего горячего источника, а не за счет сжигания топлива, а отводится к внешнему холодному источнику, а не выбросом в атмосферу; — Процессы сжатия и расширения рабочего тела протекают без теплообмена с внешней средой (адиабатно); — Отсутствуют трение между элементами шатунно — поршневой группы и гидравлическое сопротивление в клапанах и подводящих трубопроводах; — Разность температур между источником теплоты и рабочим телом бесконечно мала. 5. Какой критерий подобия является безразмерным коэффициентом теплоотдачи? Число подобия Нуссельта является безразмерным коэффициентом теплоотдачи, и определяет интенсивность теплообмена на границе жидкости и твердого тела. 6. Какой фактор следует принимать во внимание при расчете теплоотдачи при поперечном обтекании трубного пучка в теплообменном аппарате, установленном непосредственно после насоса? При расчете теплоотдачи при поперечном обтекании трубного пучка в теплообменном аппарате, установленном непосредственно после насоса следует принимать во внимание, что расположение труб в пучке может быть либо в коридорном, либо в шахматном порядках.
К характеристикам пучка относятся: – поперечный шаг пучка (S1) – расстояние между осями двух соседних труб в ряду, перпендикулярному движению жидкости; – продольный шаг пучка (S2) – расстояние между осями двух соседних труб в ряду, параллельному движению жидкости; – относительный поперечный шаг пучка – отношение S1/d; – относительный продольный шаг пучка – отношение S2/d; – количество рядов труб поперёк движения жидкости – n1;
– количество рядов труб вдоль движения жидкости – n2; 7. До какого расстояния возможно существование ламинарного пограничного слоя у вертикальной нагретой поверхности? Вначале толщина нагретого слоя мала и течение жидкости имеет струйчатый, ламинарный характер. Но по направлению движения толщина слоя увеличивается и при определенном ее значении течение жидкости становится неустойчивым, волновым, локонообразным и затем переходит в неупорядоченно-вихревое, турбулентное, с отрывом вихрей от стенки. С изменением характера движения изменяется и теплоотдача. При ламинарном движении вследствие увеличения толщины пограничного слоя коэффициент теплоотдачи по направлению движения убывает, а при турбулентном он резко возрастает и затем по высоте остается постоянным т движение, и ее положение. Около нагретых горизонтальных плоских стенок или плит движение жидкости имеет иной характер и в значительной мере зависит от положения плиты и ее размеров. Если нагретая поверхность обращена кверху, то движение протекает по схеме (рис. а). При этом если плита имеет большие размеры, то вследствие наличия с краев сплошного потока нагретой жидкости центральная часть плиты оказывается изолированной. Ее вентиляция происходит лишь за счет притока (провала) холодной жидкости сверху (рис. б). Если же нагретая поверхность обращена вниз, то в этом случае движение происходит лишь в тонком слое под поверхностью (рис. в); остальная же масса жидкости ниже этого слоя остается неподвижной. 8. Что такое «температурный напор»? Температурный напор — разность характерных температур среды и стенки (или границы раздела фаз) или двух сред, между которыми происходит теплообмен. Местный температурный напор — разность температур среды и местной температуры стенки (границы раздела фаз) либо разность температур двух сред в данном сечении теплообменной системы. Средний температурный напор — температурный напор, осреднённый по поверхности теплообмена. Произведение значения температурного напора на коэффициент теплопередачи определяет количество теплоты, передаваемое от одной среды к другой через единицу поверхности нагрева в единицу времени, то есть плотность теплового потока. Список используемой литературы. 1. Бажан П.И., Каневец Г.Е., Селиверстов В.М. Справочник по теплообменным аппаратам. – М.: Машиностроение, 1989. – 362 c. 2. Ерофеев В.Л., Семенов П.Д., Пряхин А.С. Теплотехника. – М.: ИКЦ «Академкнига», 2008. – 488 с. 3. Лебедев О.Н., Калашников С.А. Судовые энергетические установки и их эксплуатация. — М.: Транспорт, 1987. – 336 с. 4. Матвеев Ю.И., Андрусенко Е.И. Развитие и распространение дизелей в России. К 100-летию русской привилегии Г.В. Тринклера на дизельный двигатель. – Н. Новгород, Изд-во ФГОУ ВПО «ВГАВТ», 2010. – 148 с. 5. Ривкин С.Л. Термодинамические свойства газов: справочник. – 4-е изд., перераб. – М.: Энергоатомиздат, 1987. – 288 с. 6. Селиверстов В.М., Бажан П.И. Термодинамика, теплопередача, теплообменные аппараты. – М.: Транспорт, 1988. – 287 с. 7. Сизых В.А. Судовые энергетические установки. – 4-е изд., перераб. и доп. — М.: Транслит, 2006. – 352 c. 8. Шураев О.П., Пономарев Н.А. Теплотехника: Задачи по теплопередаче. – Н. Новгород: Изд-во ФГОУ ВПО «ВГАВТ», 2009. – 167 с. 🌟 ВидеоУниверсальная молярная газовая постоянная. Уравнение Менделеева - Клапейрона 10 классСкачать  Адиабатный процесс. 10 класс.Скачать  Физика. МКТ: Уравнение Менделеева-Клапейрона для идеального газа. Центр онлайн-обучения «Фоксфорд»Скачать  Уравнение состояния идеального газа | Физика 10 класс #33 | ИнфоурокСкачать  Применение первого закона термодинамики к изопроцессам. 10 класс.Скачать  Урок 172. Применение 1 закона термодинамики для различных процессовСкачать  Урок 156. Уравнение состояния идеального газа. Квазистатические процессыСкачать  Количество теплоты, удельная теплоемкость вещества. 8 класс.Скачать  Урок 194. Уравнение Ван-дер-ВаальсаСкачать  Физика 10 класс (Урок№20 - Уравнение состояния идеального газа. Газовые законы.)Скачать  Газовые законыСкачать  Решение графических задач на тему Газовые законыСкачать  Идеальный газ. Основное уравнение молекулярно-кинетической теории газов. 10 класс.Скачать  Эта тема ВСЕГДА встречается на экзамене ЦТ — Изопроцессы (Физика для чайников)Скачать  Урок 157. Изопроцессы и их графики. Частные газовые законыСкачать  Первый закон термодинамики. 10 класс.Скачать  29. Адиабатический процесс. Уравнение ПуассонаСкачать  Уравнение состояния идеального газаСкачать  |
,
,
,
,
,
,
.
.
.
.
,
равно приращению внутренней энергии dU.
,
,
,
,
,
.
.
. При изобарическом процессе Р = const. Следовательно, из (4.2.7) получим:
.
.
.
Внутренняя энергия. Работа и теплота Теплоёмкости одноатомных и многоатомных газов 
Серьёзное исследование адиабатических процессов началось в XVIII веке [1] . 
) системы со средой сводится только к последним двум процессам [6] . Поэтому, первое начало термодинамики в этом случае приобретает вид [7] [Комм 1]
— изменение внутренней энергии тела, 
— работа, совершаемая системой.
— температура системы, 
— теплота, полученная системой. Благодаря этому адиабатический процесс может быть составной частью обратимого цикла [8] .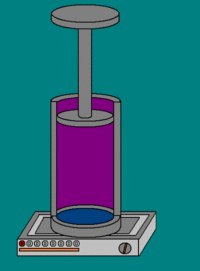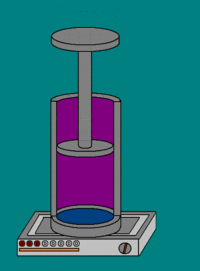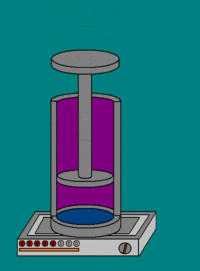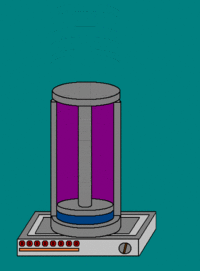 
совершать работу [9] [10]
— давление газа, 
— малое приращение объёма. Аналогично видно, что уравнение выполняется и для сосудов с произвольной поперечной формой сечения. Данное уравнение справедливо и при расширении на произвольных объёмах. Для этого достаточно разбить поверхность расширения на элементарные участки 
на которых расширение одинаково [9] .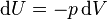
, 
— дифференциальное выражение для работы, 
— внешние параметры, которые меняются при совершении работы, 
.
, 
; 
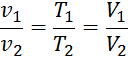
— уравнение Майера для одного моля газа.
— универсальная газовая постоянная, 
— молярная теплоёмкость при постоянном давлении, 
— молярная теплоёмкость при постоянном объёме.
, где:
— характерный размер;
— коэффициент теплопроводности среды;
— коэффициент теплоотдачи;
— тепловой поток за счёт конвекции;
— тепловой поток за счёт теплопроводности.
При свободном движении жидкости в пограничном слое температура жидкости изменяется от tc до tж , а скорость — от нуля у стенки проходит через максимум и на большом удалении от стенки снова равна нулю).