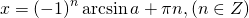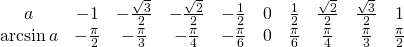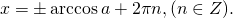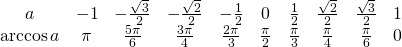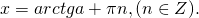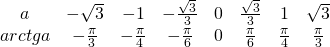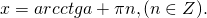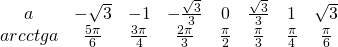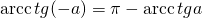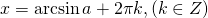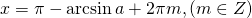Формулы корней тригонометрических уравнений в таблице для синуса (2 видео)

РЕШЕНИЕ ПРОСТЕЙШИХ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ

Простейшими тригонометрическими уравнениями называют уравнения

Чтобы рассуждения по нахождению корней этих уравнений были более наглядными, воспользуемся графиками соответствующих функций.

19.1. Уравнение cos x = a

Объяснение и обоснование

Корни уравненияcosx=a.

2.Частые случаи решения уравнения sin x = a.

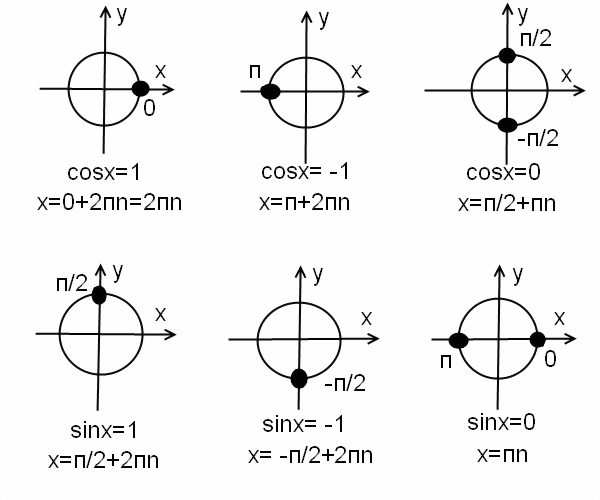
Полезно помнить специальные записи корней уравнения при a = 0, a = -1, a = 1, которые можно легко получить, используя как ориентир единичную окружность (рис 2).

Учитывая, что синус равен ординате соответствующей точки единичной окружности, получаем, что sin x = 0 тогда и только тогда, когда соответствующей точкой единичной окружности является точка C или тока D. Тогда

Аналогично sin x = 1 тогда и только тогда, когда соответствующей точкой единичной окружности является точка A, следовательно,

Также sin x = -1 тогда и только тогда, когда соответствующей точкой единичной окружности является точка B, таким образом,

Примеры решения задач

Замечание. Ответ к задаче 1 часто записывают в виде:

19.3. Уравнения tg x = a и ctg x = a

Объяснение и обоснование

1.Корни уравнений tg x = a и ctg x = a

Рассмотрим уравнение tg x = a. На промежутке функция y = tg x возрастает (от -∞ до +∞). Но возрастающая функция принимает каждое свое значение только в одной точке ее области определения, поэтому уравнение tg x = a при любом значении a имеет на этом промежутке только один корень, который по определению арктангенса равен: x₁ = arctg a и для этого корня tg x = a.

Функция y = tg x периодическая с периодом π, поэтому все остальные корни отличаются от найденного на πn (n ∈ Z). Получаем следующую формулу корней уравнения tg x = a:

При a=0 arctg 0 = 0, таким образом, уравнение tg x = 0 имеет корни x = πn (n ∈ Z).

Рассмотрим уравнение ctg x = a. На промежутке (0; π) функция y = ctg x убывает (от +∞ до -∞). Но убывающая функция принимает каждое свое значение только в одной точке ее области определения, поэтому уравнение ctg x = a при любом значении a имеет на этом промежутке только один корень, который по определению арккотангенса равен: x₁=arсctg a.

Функция y = ctg x периодическая с периодом π, поэтому все остальные корни отличаются от найденного на πn (n ∈ Z). Получаем следующую формулу корней уравнения ctg x = a:

таким образом, уравнение ctg x = 0 имеет корни

Примеры решения задач

Вопросы для контроля

Какие уравнения называют простейшими тригонометрическими?
Запишите формулы решения простейших тригонометрических уравнений. В каких случаях нельзя найти корни простейшего тригонометрического уравнения по этим формулам?
Выведите формулы решения простейших тригонометрических уравнений.
Обоснуйте формулы решения простейших тригонометрических уравнений для частных случаев.

Упражнения

Решите уравнение (1-11)

Найдите корни уравнения на заданном промежутке (12-13)

Содержание

Узнать ещё
Формулы тригонометрических уравнений
21 комментарий на «Формулы тригонометрических уравнений»
Тригонометрические формулы. Их вывод
🔍 Видео

Видео:Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

Узнать ещё

Знание — сила. Познавательная информация

Видео:18+ Математика без Ху!ни. Формулы ПриведенияСкачать

Формулы тригонометрических уравнений

Для удобной работы все формулы для решения простейших тригонометрических уравнений, включая частные случаи, а также таблицы арксинусов, арккосинусов, арктангенсов и арккотангенсов собраны на одной странице.

I. sin x =a

При │a│>1 это уравнение решений не имеет.

При │a│не превосходящем 1 уравнение имеет бесконечное множество решений:

Таблица арксинусов

II. cos x=a

При │a│>1 это уравнение решений не имеет.

При │a│не превосходящем 1 уравнение имеет бесконечное множество решений:

Таблица арккосинусов

Частные случаи синуса и косинуса:

III. tg x=a

Уравнение имеет бесконечное множество решений при любых значениях a.

Таблица арктангенсов

IV. ctg x = a

Уравнение имеет бесконечное множество решений при любых значениях a.

Таблица арккотангенсов

21 комментарий на «Формулы тригонометрических уравнений»

Отличный сайт, спасибо, помог.

Спасибо за отличную оценку!
Я рада, что сайт Вам помог.

Пожалуйста!) Успехов Вам в учебе!

Сайт действительно хороший =)
Интересно, просто, ясно.
Спасибо Вам, Светлана Иванова!

Ариша, спасибо за теплый отзыв!

Опечатка в таблице арккотангенсов )
А так все отлично, хорошая статья

Опечатку исправила. Спасибо!

Не силен в этих науках и школу прогуливал всегда!Жалею теперь об этом!Но вот беда ума не могу приложить что может значить arccos0,932 что это?с чем его едят ?И как его посчитать!Смотрю на выше написанное и не пойму как мне это применить!Помгите убогому!

Антон, разобраться в математике можно в любом возрасте, было бы желание. Но придется потрудиться (а где без этого?).
arccos 0,932 — это такое число из промежутка [0;П], косинус которого равен 0,932.
Можно открыть таблицу Брадиса и найти угол, косинус которого равен этому числу: [0,932 approx cos ]Далее, если требуется ответ представить в радианах, градусы переводим в радианы. [pi = , Rightarrow = frac<>,][ = 21 cdot frac<> = frac<><>.]Отсюда [arccos 0,932 approx frac<><>.]
Если же arccos 0,932 появился в ходе решения тригонометрического уравнения — оставляйте его в таком виде.
Например:[cos x = 0,932][x = pm arccos 0,932 + 2pi n,n in Z.]Все, дальше ничего считать не надо (запись в таком виде — точное решение, а при нахождении арккосинуса ответ станет не точным, а приближенным. Поэтому его и не принято упрощать).

Светлана спасибо вам большое за помощь)Есть еще один вопросик я весь google перекопал. Какова единица измерения числа которое получается в результате вычисления cos или sin угла например sin47.376 градусов =0,735??какая единица измерения Arccos0,735=42.692. что это за величина и какая ее единица измерения?Голова дымит, а надо знать это,а то на работу не возьмут!

Косинус угла и синус угла — это просто число (в пределах от -1 до 1). Неважно, задан угол в градусах или в радианах.
Теперь — об арксинусах и арккосинусах. Если использовать таблицу Брадиса, arccos0,735 ищем как угол, косинус которого равен 0,735. [cos approx 0,735]То есть Ваши 42.692, насколько я понимаю, градусы. Но в градусах значения арккосинуса и арксинуса не оставляют. Нужно перевести в радианы. [ = 42 cdot frac<> = frac<><>.]7П/30 радиан, радианы не пишут. Радианная мера позволяет от градусной меры угла перейти к числам, чтобы потом графики тригонометрических функций в декартовой системе координат строить можно было, например.

Спасибо вы целиком и полностью удовлетворили мой интерес!

Спасибо за шпору =), пошел сдавать

Ещё о таблицах. Точнее их отсутствии…
на калькуляторе мы получаем cos, затем arccos. Верно ли я понимаю, что значения arccos вычисляются в радианной мере, и после этого следует обязательно перевести в градусную меру? (Таблицы Брадиса, также как и любые другие, идут уже (!) с перерасчетом радианов в градусы. ) …но таблиц нет, к примеру. Некоторые on-line–научные калькуляторы имеют опцию переключения с градусов в радианы и/или наоборот; при этом по умолчанию может стоять опция (галочка) как радианной меры, так и градусной.
Вопрос: в каких случаях надобно переходить с радианов в градусы?
(функции MS Office Excel, например, предусматривают именно трёхстадийный процесс вычисления: cos, arccos, затем перевод радианов в градусы).
И ещё вопросик: Таблицы содержат значения синусов/косинусов только для острых углов в ПРЯМОУГОЛЬНОМ треугольнике?
Пример, имеется равносторонний треугольник (все стороны и углы равны), нам надо найти угол (мы его не знаем). Сторона (все три стороны равны) = 60 см. Т.е. поделив все [равные] стороны получим
sin = cos = tg = ctg = sec = cosec = 1
но по этому значению угол [каковой реально 60°] найти в таблицах невозможно. Спасибо!

Nick, прошу прощения, что затянула с ответом. Меня мучает совесть(
С калькулятором я практически не работаю, предпочитаю считать либо устно, либо письменно. Если нужно, пользуюсь таблицами Брадиса. Над нюансами вычислений с калькулятором не задумывалась.
Значения синуса и косинуса зависят только от угла, но не от вида треугольника. Мы вводим определение синуса в прямоугольном треугольнике как отношение противолежащего катета к гипотенузе, потом расширяем определение, называя синусом угла альфа ординату точки единичной окружности, полученной из точки (1;0) поворотом на угол альфа.
Синус угла в произвольном треугольнике можно найти посредством через теорему синусов, через площадь треугольника (из формулы S=1/2 ab sin α), или провести высоту и рассмотреть прямоугольный треугольник.
В таблице Брадиса значения тригонометрических функций даны только для острых углов. Для тупых углов значения находят с помошью формул приведения.

Объясните мне, пожалуйста, если п принадлежит Z, где п — , Z — .я не могу понять когда п четное, п — нечетное и что такое Z?

Тамара, семейство решений для общего случая уравнений sinx=a

можно разбить на два семейства решений:
1) при n=2k (то есть для чётных)

2) при n=2m+1 (то есть для нечётных)

Z — множество целых чисел, то есть 0; ±1; ±2; ±3; …

Страница интересная,но я не нашла частные случаи для тангенса и котангенса.Помогите пожалуйста(очень нужно

Евгения, формул частных случаем для тангенса и котангенса нет. Иногда частными случаями называют уравнения вида tgx=1; tgx=-1; ctgx=1; ctgx=-1, но общая формула верна и для каждого из этих случаев.

Видео:Тригонометрические уравнения. ЕГЭ № 12 | Математика | TutorOnline tutor onlineСкачать

Тригонометрические формулы. Их вывод

Наиболее часто встречающиеся тригонометрические формулы:

(blacktriangleright) Основные тождества: [begin hline sin^2 alpha+cos^2 alpha =1& mathrm, alpha cdot mathrm, alpha =1 \ &(sinalphane 0, cosalphane 0)\[0.5ex] hline &\ mathrm, alpha=dfrac &mathrm, alpha =dfrac \&\ 1+mathrm^2, alpha =dfrac1 & 1+mathrm^2, alpha=dfrac1\&\ (cosalphane 0)& (sinalphane 0) \ hline end]

(blacktriangleright) Формулы сложения углов: [begin hline &\ sin=sinalphacdot cosbetapm sinbetacdot cosalpha & cos=cosalphacdot cosbeta mp sinalphacdot sinbeta\ &\ hline &\ mathrm, (alphapm beta)=dfrac<mathrm, alphapm mathrm, beta><1 mp mathrm, alphacdot mathrm, beta> & mathrm, (alphapmbeta)=-dfrac<1mp mathrm, alphacdot mathrm, beta><mathrm, alphapm mathrm, beta>\&\ cosalphacosbetane 0&sinalphasinbetane 0\ hline end]

(blacktriangleright) Формулы двойного и тройного углов: [begin hline sin =2sin alphacos alpha & qquad &qquad & cos=cos^2alpha -sin^2alpha\ sin alphacos alpha =dfrac12sin && & cos=2cos^2alpha -1\ & & & cos=1-2sin^2 alpha\ hline &&&\ mathrm, 2alpha = dfrac<2mathrm, alpha><1-mathrm^2, alpha> && & mathrm, 2alpha = dfrac<mathrm^2, alpha-1><2mathrm, alpha>\&&&\ cosalphane 0, cos2alphane 0 &&& sinalphane 0, sin2alphane 0\ hline &&&\ sin =3sin alpha -4sin^3alpha && & cos=4cos^3alpha -3cos alpha\&&&\ hline end]

(blacktriangleright) Формулы понижения степени: [begin hline &&&\ sin^2alpha=dfrac<1-cos>2 &&& cos^2alpha=dfrac<1+cos>2\&&&\ hline end]

(blacktriangleright) Формулы произведения функций: [begin hline \ sinalphasinbeta=dfrac12bigg(cos-cosbigg)\\ cosalphacosbeta=dfrac12bigg(cos+cosbigg)\\ sinalphacosbeta=dfrac12bigg(sin+sinbigg)\\ hline end]

(blacktriangleright) Выражение синуса и косинуса через тангенс половинного угла: [begin hline &\ sin=dfrac<2mathrm, alpha><1+mathrm^2, alpha> & cos=dfrac<1-mathrm^2, alpha><1+mathrm^2, alpha>\&\ cosalphane 0 & sinalphane 0\ hline end]

(blacktriangleright) Формула вспомогательного аргумента: [begin hline text\ hline \ sinalphapm cosalpha=sqrt2cdot sin<left(alphapm dfrac4right)>\\ sqrt3sinalphapm cosalpha=2sin<left(alphapm dfrac6right)>\\ sinalphapm sqrt3cosalpha=2sin<left(xpm dfrac3right)>\\ hline text\ hline\ asinalphapm bcosalpha=sqrtcdot sin, cosphi=dfrac a<sqrt >, sinphi=dfrac b<sqrt >\\ hline end]

Зная идею вывода формул, вы можете запомнить лишь несколько из них. Тогда остальные формулы вы всегда сможете быстро вывести.

Вывод всех основных тождеств был рассказан в предыдущем разделе “Введение в тригонометрию”.

(blacktriangleright) Вывод формулы косинуса разности углов (cos=cosalphacosbeta+sinalphasinbeta)

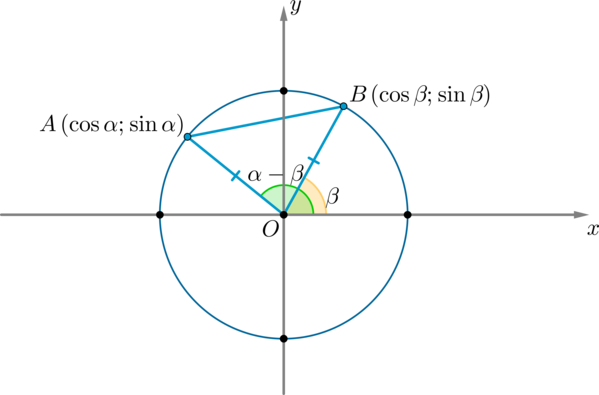
Рассмотрим тригонометрическую окружность и на ней углы (alpha) и (beta) . Пусть этим углам соответствуют точки (A) и (B) соответственно. Тогда координаты этих точек: (A(cosalpha;sinalpha), B(cosbeta;sinbeta)) .