f(x)=0, где f(x) – произвольная функция, наиболее распространенная в инж. Практике задача по отысканию корней.
Выбор метода решения зависит от вида f(x). Для численного решения нелинейных уравнений применяются только итерационные методы.
Задача нахождения корней состоит из 2 этапов:
1. Отделение корней – определение числа корней и их примерного расположения на числовой оси.
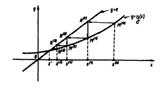
Наиболее применим графический способ отделения корней, т. е. отыскание точек пересечения ф. f(x) с осью абсцисс:
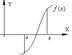
2. Уточнение корней – вычисление каждого корня с заданной степенью точности.
Классификация методов уточнения корней :
1) Метод половинного деления отрезка(дихотомии).

Достоинства: прост и надежен, всегда сводится к решению независимо от вида ф. f(x). Недостаток: самый медленный из всех известных методов уточн. Корня.

Достоинство: простота. Недостаток: быстрота сходимости к решению сильно зависит от вида ф. f(x).

В качестве приближения к корню ищется точка пересечения касательной с осью абсцисс.
Достоинство: высокая скорость. Недостатки: ограничения на вид ф. (должна быть дифференцируема, f’(x) и f’’(x) не должны менять знак на интервале уточнения корня).
4) Комбинированный метод – объединение методов хорд и касательных.

Достоинство: работает быстрее, чем методы хорд и касательных. Недостатки: f(x) должна быть дифференцируема; f’(x) иf’’(x) не должны менять знак на интервале уточнения корня; трудности с дифф-ем f(x).
5) Метод простой итерации.
Исходное нелинейное уравнения заменяется равносильным уравнением x=g(x)и с помощью сходящегося итерационного процесса происходит приближение к корню, пока не достигнет предела заданной погрешности Е.
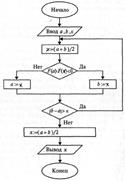
45)Уточнение корня нелинейного уравнения методом половинного деления(дихотомии). Алгоритм. Требуется вычислить корень уравнения f(x)=0 на [a;b] с заданной погрешностью Е. Отрезок [a;b], содержащий единственный корень, делят на 2 половины, отбрасывают ту из них, где нет корня. Процесс продолжается до тех пор, пока длина отрезка не станет меньше заданной погрешности Е.  Алгоритм метода: Алгоритм метода: |




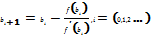
Видео:Метод Ньютона (метод касательных) Пример РешенияСкачать

Численные методы: решение нелинейных уравнений
Задачи решения уравнений постоянно возникают на практике, например, в экономике, развивая бизнес, вы хотите узнать, когда прибыль достигнет определенного значения, в медицине при исследовании действия лекарственных препаратов, важно знать, когда концентрация вещества достигнет заданного уровня и т.д.
В задачах оптимизации часто необходимо определять точки, в которых производная функции обращается в 0, что является необходимым условием локального экстремума.
В статистике при построении оценок методом наименьших квадратов или методом максимального правдоподобия также приходится решать нелинейные уравнения и системы уравнений.
Итак, возникает целый класс задач, связанных с нахождением решений нелинейных уравнений, например, уравнения 

В простейшем случае у нас имеется функция 
Каждому значению x из этого отрезка мы можем сопоставить число 
Нам нужно найти такое значение 


Визуально нам нужно определить точку пересечения графика функции 
Видео:Отделение корней уравнений аналитическим методом. Уточнение корней методом половинного деленияСкачать

Метод деления пополам
Простейшим методом нахождения корней уравнения 
Этот метод является интуитивно ясным и каждый действовал бы при решении задачи подобным образом.
Алгоритм состоит в следующем.
Предположим, мы нашли две точки 




Поделим отрезок 

Тогда либо 

Оставим ту половину отрезка, для которой значения на концах имеют разные знаки. Теперь этот отрезок снова делим пополам и оставляем ту его часть, на границах которой функция имеет разные знаки, и так далее, достижения требуемой точности.
Очевидно, постепенно мы сузим область, где находится корень функции, а, следовательно, с определенной степенью точности определим его.
Заметьте, описанный алгоритм применим для любой непрерывной функции.
К достоинствам метода деления пополам следует отнести его высокую надежность и простоту.
Недостатком метода является тот факт, что прежде чем начать его применение, необходимо найти две точки, значения функции в которых имеют разные знаки. Очевидно, что метод неприменим для корней четной кратности и также не может быть обобщен на случай комплексных корней и на системы уравнений.
Порядок сходимости метода линейный, на каждом шаге точность возрастает вдвое, чем больше сделано итераций, тем точнее определен корень.
Видео:Алгоритмы. Нахождение корней уравнений методом деления отрезка пополам.Скачать

Метод Ньютона: теоретические основы
Классический метод Ньютона или касательных заключается в том, что если 




Уравнение касательной к функции 

В уравнении касательной положим 

Тогда алгоритм последовательных вычислений в методе Ньютона состоит в следующем:
Сходимость метода касательных квадратичная, порядок сходимости равен 2.
Таким образом, сходимость метода касательных Ньютона очень быстрая.
Запомните этот замечательный факт!
Без всяких изменений метод обобщается на комплексный случай.
Если корень 
Упражнение 1. Найти с помощью метода касательных решение уравнения 
Упражнение 2. Найти с помощью метода касательных решение уравнения 
К недостаткам метода Ньютона следует отнести его локальность, поскольку он гарантированно сходится при произвольном стартовом приближении только, если везде выполнено условие 
Недостатком метода Ньютона является необходимость вычисления производных на каждом шаге.
Видео:Численное решение уравнений, урок 3/5. Метод хордСкачать

Визуализация метода Ньютона
Метод Ньютона (метод касательных) применяется в том случае, если уравнение f(x) = 0 имеет корень 
1) функция y= f(x) определена и непрерывна при 
2) f(a)·f(b) 0. Таким образом, выбирается точка с абсциссой x0, в которой касательная к кривой y=f(x) на отрезке [a;b] пересекает ось Ox. За точку x0 сначала удобно выбирать один из концов отрезка.
Рассмотрим метод Ньютона на конкретном примере.
Пусть нам дана возрастающая функция y = f(x) =x 2 -2, непрерывная на отрезке (0;2), и имеющая f ‘(x) = 2x > 0 и f »(x) = 2 > 0.
Уравнение касательной в общем виде имеет представление:
В нашем случае: y-y0=2x0·(x-x0). В качестве точки x0 выбираем точку B1(b; f(b)) = (2,2). Проводим касательную к функции y = f(x) в точке B1, и обозначаем точку пересечения касательной и оси Ox точкой x1. Получаем уравнение первой касательной:y-2=2·2(x-2), y=4x-6.
Точка пересечения касательной и оси Ox: x1 =
Рисунок 2. Результат первой итерации
Затем находим точку пересечения функции y=f(x) и перпендикуляра, проведенного к оси Ox через точку x1, получаем точку В2 =(1.5; 0.25). Снова проводим касательную к функции y = f(x) в точке В2, и обозначаем точку пересечения касательной и оси Ox точкой x2.
Точка пересечения касательной и оси Ox: x2 = 
Рисунок 3. Вторая итерация метода Ньютона
Затем находим точку пересечения функции y=f(x) и перпендикуляра, проведенного к оси Ox через точку x2, получаем точку В3 и так далее.
В3 = (
Рисунок 4. Третий шаг метода касательных
Первое приближение корня определяется по формуле:

Второе приближение корня определяется по формуле:

Третье приближение корня определяется по формуле:

Таким образом, i-ое приближение корня определяется по формуле:
Вычисления ведутся до тех пор, пока не будет достигнуто совпадение десятичных знаков, которые необходимы в ответе, или заданной точности e — до выполнения неравенства |xi—xi-1|
using namespace std;
float f(double x) //возвращает значение функции f(x) = x^2-2
float df(float x) //возвращает значение производной
float d2f(float x) // значение второй производной
int _tmain(int argc, _TCHAR* argv[])
int exit = 0, i=0;//переменные для выхода и цикла
double x0,xn;// вычисляемые приближения для корня
double a, b, eps;// границы отрезка и необходимая точность
cin>>a>>b; // вводим границы отрезка, на котором будем искать корень
cin>>eps; // вводим нужную точность вычислений
if (a > b) // если пользователь перепутал границы отрезка, меняем их местами
if (f(a)*f(b)>0) // если знаки функции на краях отрезка одинаковые, то здесь нет корня
cout 0) x0 = a; // для выбора начальной точки проверяем f(x0)*d2f(x0)>0 ?
xn = x0-f(x0)/df(x0); // считаем первое приближение
cout eps) // пока не достигнем необходимой точности, будет продолжать вычислять
xn = x0-f(x0)/df(x0); // непосредственно формула Ньютона
> while (exit!=1); // пока пользователь не ввел exit = 1
Посмотрим, как это работает. Нажмем на зеленый треугольник в верхнем левом углу экрана, или же клавишу F5.
Если происходит ошибка компиляции «Ошибка error LNK1123: сбой при преобразовании в COFF: файл недопустим или поврежден», то это лечится либо установкой первого Service pack 1, либо в настройках проекта Свойства -> Компоновщик отключаем инкрементную компоновку.
Рис. 4. Решение ошибки компиляции проекта
Мы будем искать корни у функции f(x) = x2-2.
Сначала проверим работу приложения на «неправильных» входных данных. На отрезке [3; 5] нет корней, наша программа должна выдать сообщение об ошибке.
У нас появилось окно приложения:
Рис. 5. Ввод входных данных
Введем границы отрезка 3 и 5, и точность 0.05. Программа, как и надо, выдала сообщение об ошибке, что на данном отрезке корней нет.
Рис. 6. Ошибка «На этом отрезке корней нет!»
Выходить мы пока не собираемся, так что на сообщение «Exit?» вводим «0».
Теперь проверим работу приложения на корректных входных данных. Введем отрезок [0; 2] и точность 0.0001.
Рис. 7. Вычисление корня с необходимой точностью
Как мы видим, необходимая точность была достигнута уже на 4-ой итерации.
Чтобы выйти из приложения, введем «Exit?» => 1.
Видео:Численное решение уравнений, урок 1/5. Локализация корняСкачать
Метод секущих
Чтобы избежать вычисления производной, метод Ньютона можно упростить, заменив производную на приближенное значение, вычисленное по двум предыдущим точкам:

Итерационный процесс имеет вид:
где 
Это двухшаговый итерационный процесс, поскольку использует для нахождения последующего приближения два предыдущих.
Порядок сходимости метода секущих ниже, чем у метода касательных и равен в случае однократного корня 
Эта замечательная величина называется золотым сечением:
Убедимся в этом, считая для удобства, что 
Таким образом, с точностью до бесконечно малых более высокого порядка
Отбрасывая остаточный член, получаем рекуррентное соотношение, решение которого естественно искать в виде 
После подстановки имеем: 
Для сходимости необходимо, чтобы 

Поскольку знание производной не требуется, то при том же объёме вычислений в методе секущих (несмотря на меньший порядок сходимости) можно добиться большей точности, чем в методе касательных.
Отметим, что вблизи корня приходится делить на малое число, и это приводит к потере точности (особенно в случае кратных корней), поэтому, выбрав относительно малое 

Как только начнется рост, вычисления прекращают и последнюю итерацию не используют.
Такая процедура определения момента окончания итераций называется приемом Гарвика.
Видео:Метод половинного деления. ДихотомияСкачать

Метод парабол
Рассмотрим трехшаговый метод, в котором приближение 



Для этого заменим, аналогично методу секущих, функцию 



В форме Ньютона она имеет вид:
Точка 

Порядок сходимости метода парабол выше, чем у метода секущих, но ниже, чем у метода Ньютона.
Важным отличием от ранее рассмотренных методов, является то обстоятельство, что даже если 

Этот метод очень удобен для поиска корней многочленов высокой степени.
Видео:Алгоритмы. Нахождение корней уравнения методом хордСкачать

Метод простых итераций
Задачу нахождения решений уравнений можно формулировать как задачу нахождения корней: 

Пусть 




По теореме Банаха существует и единственна неподвижная точка
Она может быть найдена как предел простой итерационной процедуры
где начальное приближение 

Если функция 

Таким образом, если производная меньше единицы, то 
Условие 



Рассмотрим уравнение: 
Если в качестве 




Однако можно в качестве 


Эти итерации сходятся к неподвижной точке для любого начального приближения 
Действительно, в первом случае 




Рассмотрим 
т.е. такой итерационный процесс всегда сходится.
Метод Ньютона представляет собой частный случай метода простых итераций.
Здесь 


то если 



Если 
Поскольку 
Таким образом, сходимость метода Ньютона очень быстрая.
Видео:Метод касательных (метод Ньютона)Скачать

Нахождение всех корней уравнения
Недостатком почти всех итерационных методов нахождения корней является то, что они при однократном применении позволяют найти лишь один корень функции, к тому же, мы не знаем какой именно.
Чтобы найти другие корни, можно было бы брать новые стартовые точки и применять метод вновь, но нет гарантии, что при этом итерации сойдутся к новому корню, а не к уже найденному, если вообще сойдутся.
Для поиска других корней используется метод удаления корней.
Пусть 







Применяя тот или иной метод нахождения корней к функции 



Повторяя указанную процедуру, можно найти все корни 
Заметим, что когда мы производим деление на тот или иной корень 


Чтобы избежать этого, с помощью вспомогательных функций вычисляются лишь первые итерации, а окончательные проводятся по исходной функции 
Мы рассмотрели решение уравнений только в одномерном случае, нахождение решений многомерных уравнений существенно более трудная задача.
Видео:Метод касательных приближенного нахождения корня уравненияСкачать

Методические указания
Министерство образования И НАУКИ Российской Федерации
ДАГЕСТАНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
КАФЕДРА ИНФОРМАЦИОННЫХ СИСТЕМ В ЭКОНОМИКЕ
к выполнению лабораторного практикума
по дисциплине «Вычислительные методы»
Часть 1. Численное решение нелинейных уравнений
Махачкала, 2004 г.
Методические указания к выполнению лабораторного практикума по дисциплине «Вычислительные методы». Часть 1 — Численное решение нелинейных уравнений. Махачкала, ДГТУ, 2004,
Методические указания предназначены для студентов дневной и заочной форм обучения специальностей 351401 — «Прикладная информатика в экономике» и 351403 — «Прикладная информатика в юриспруденции».
Часть 1 методических указаний содержит краткие теоретические сведения о численных методах решения нелинейных уравнений, блок-схемы алгоритмов, методические примеры, индивидуальные задания к выполнению лабораторных работ.
Составители: зав. кафедрой ИСЭ, д. э.н., проф. ;
ст. преп. кафедры ИСЭ, к. ф.-м. н.
научно-исследовательского и технологического
института при Правительстве Республики,
Видео:Урок 6 УРАВНЕНИЕ И ЕГО КОРНИ 7 КЛАСССкачать

, зав. кафедрой высшей
математики ДГТУ, профессор
Печатается по решению Совета Дагестанского технического университета
от «______»______________2004 г.
Внедрение ЭВМ во все сферы человеческой деятельности требует от специалистов разного профиля овладения навыками использования ВТ. Органической частью фундаментальной подготовки студентов является изучение таких направлений применения ЭВМ, как основы вычислительной техники и программирования, численные методы решения инженерных и экономических задач, методы оптимизации и оптимального управления и т. д.
Данные методические указания посвящены вопросам практического использования вычислительных методов.
Вычислительные методы и алгоритмы разрабатывают и исследуют, как правило, высококвалифицированные специалисты-математики. Что касается подавляющей части студентов, то для них главной задачей является понимание основных идей методов, особенностей и областей их применения.
В данной работе в кратком виде приводятся основные необходимые сведения о вычислительных методах решения прикладных задач. Для рассматриваемых методов приводятся основные теоретические сведения, методические примеры, блок-схемы алгоритмов, а также индивидуальные задания.
В нумерации формул первая цифра соответствует номеру лабораторной работы, а вторая – порядковому номеру формулы в лабораторной работе.
Решение задач ориентировано на использование ПЭВМ. Указания являются полезными при выполнении лабораторных работ по курсам:
— прогнозирование социально-экономических процессов в Дагестане;
— имитационное моделирование экономических процессов;
— статистика правонарушений и экономические преступления в РД;
— анализ и прогнозирование правонарушений;
Структура отчета по лабораторной работе
1. Постановка задачи.
2. Теоретические сведения о методе решения задачи.
3. Блок-схема алгоритма решения задачи.
4. Текст программы.
5. Результаты и их анализ.
Отчет по лабораторной работе студент пишет от руки в ученической тетради и защищает его перед преподавателем.
Лабораторная работа №1
РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
методом половинного деления
В общем случае нелинейное уравнение можно записать в виде:

где функция 

Всякое число 




Однократный корень называется простым.
Два уравнения F(x) и G(x) называются равносильными (эквивалентными), если всякое решение каждого из них является решением и для другого, т. е. множества решений этих уравнений совпадают.
Нелинейные уравнения с одним неизвестным подразделяются на алгебраические и трансцендентные.
Уравнение (1.1) называется алгебраическим, если функция является алгебраической функцией. Путем алгебраических преобразований из всякого, алгебраического уравнения можно получить уравнение в канонической форме:
где 



Известно, что всякое алгебраическое уравнение имеет, по крайней мере, один корень вещественный или комплексный.
При приведении алгебраического уравнения (1.1) к канонической форме будем иметь те же корни, что и для исходного уравнения. Однако при этом могут появиться некоторые лишние корни. Например, уравнение
может быть приведено к канонической форме:

Если функция F(x) не является алгебраической — показательной, логарифмической, тригонометрической, то уравнение (1.1) называется трансцендентным. Примерами трансцендентных уравнений являются:
В некоторых случаях решение трансцендентных уравнений можно свести к решению алгебраических уравнений.
Поскольку подавляющее большинство нелинейных уравнений с одной переменной не решается путем аналитических преобразований (точными методами), на практике их решают только численными методами. Решить такое уравнение — это значит: установить, имеет ли оно корни, сколько корней, и найти значения корней с заданной точностью. Задача численного нахождения действительных и комплексных корней уравнения (1.1) обычно состоит из двух этапов: отделение корней, т. е. нахождение достаточно малых окрестностей рассматриваемой области, в которых содержится одно значение корня, и уточнение корней, т. е. вычисление корней с заданной степенью точности в некоторой окрестности.
В дальнейшем будем рассматривать численные методы нахождения действительных корней уравнения (1.1). Наиболее распространенными на практике численными методами решения уравнения (1.1) являются: метод половинного деления, метод хорд, метод касательных (Ньютона), комбинированный метод, метод итераций. Применение того или иного, численного метода для решения уравнения (1.1) зависит от числа корней, задания исходного приближения и поведения функции F(x).
Остановимся подробно на наиболее часто используемых на ЭВМ методе половинного деления
1.2. ОТДЕЛЕНИЕ КОРНЕЙ
Первый этап численного решения уравнения (1.1) состоит в отделении корней, т. е. в установлении «тесных» промежутков, содержащих только один корень. Отделение корней во многих случаях можно произвести графически. Принимая во внимание, что действительные корни уравнения (1.1)—это точки пересечения графика функции F(x) с осью абсцисс, достаточно построить график F(x) и отметить на оси Ох отрезки, содержащие по одному корню. Построение графиков часто удается сильно упростить, заменив уравнение (1.1) равносильным ему уравнением

В этом случае строятся графики функций f1(x) и f2(x), а потом на оси Ох отмечаются отрезки, локализующие абсциссы точек пересечения этих графиков.
ПримерДля графического отделения корней уравнения sin2х – lnx = 0 выгодно отдельно построить графики функций sin2x и ln (х) (рис. 1).
Из графика следует, что уравнение имеет корень, принадлежащий отрезку [1; 1,5|.
В сомнительных случаях графическое отделение корней необходимо подкрепить вычислениями. При этом полезно использовать следующие очевидные положения:
1) если непрерывная на отрезке [а; b] функция F(x) принимает на его концах значения разных знаков (т. е. F(a)∙F(b) 0, так что отрезком отделения корней можно считать [1,3; 1,5].
Для отделения корней можно эффективно использовать ЭВМ.
Пусть имеется уравнение F(x)=0, причем можно считать, что все интересующие нас корни находятся на отрезке [A; B], в котором функция F(x) определена, непрерывна и F(A)∙F(B) -10
при x 1. Тогда вместо функции у = φ(х) рассмотрим функцию х = g(у), обратную для φ(х). Будем теперь решать уравнение у = g(у) (или, в старых обозначениях, х = g(х)). По свойству производных обратных функций теперь на отрезке [а; b] будет иметь место:

так что для уравнения х=g(х), равносильного исходному, условие (3) теоремы 2.1 оказывается выполненным.
Для ручных вычислении (с помощью калькулятора) корня по методу итераций может использоваться расчетная таблица, содержащая обычную пооперационную запись формулы φ(х) (табл. 2.1). Полученное в результате одного «прохода» вычислений в правом столбце очередное приближение корня сразу же переносится в следующую строку столбца хп и процесс повторяется.
Пример 2.1. Уточнить с помощью калькулятора корень уравнения sin2x — lnx = 0 на отрезке [1,3;1,5] методом итераций с точностью до 10-4.
Исходное уравнение можно привести к итерационному виду несколькими способами, например:
Исследуем возможность применения к полученным представлениям метода итераций.
1. В первом случае φ(х) = ехр (sin2х). Функция f(x) определена и дифференцируема на отрезке [1,3; 1,5|, однако второе условие теоремы 1.1 не выполняется: с помощью калькулятора получаем f(1,3)= 1,674478, т. е. уже в левом конце отрезка значение функции выходит за пределы отрезка.
2. Рассмотрим второе представление. Уравнение, равносильное исходному на отрезке [1,3; 1,5], получается при
Здесь φ(х) =(π – arcsin lnx)/2. Замечаем, что для всех х отрезка [1,3; 1,5], будет 
Вычислим ее значение в концах отрезка [1,3; 1,5]:
Так как полученные значения входят в отрезок [1,3; 1,5], а функция φ(x) монотонна, то отсюда следует, что второе условие теоремы 2.1 выполняется.
Для проверки третьего условия исследуем модуль производной функции φ(x) на отрезке [1,3; 1,5]:

Найдем производную функции

Заметим, что φ1′(х) на отрезке [1,3; 1,5] всюду отрицательна. Это значит, что φ1(х) = |f‘(x)| на этом отрезке убывает и достигает максимума на левом конце: | φ'(1,3)| =0,3846153.
Таким образом, условие (3) теоремы 2.1 будет выполнено, если принять q = 0,39. Уточнение корня уравнения (2.13) с нулевым значением x0 =1,4 на калькуляторе приведено в таблице 2.2.
Используя оценочную формулу (2.11) и принимая во внимание исходные значения ε = 10-4 и (q = 0,39, уже для третьего приближения имеем: х3 — x2
🔥 Видео
Метод половинного деления решение нелинейного уравненияСкачать

Метод простых итераций пример решения нелинейных уравненийСкачать

Методы уточнения корней. Метод дихотомииСкачать

10 Численные методы решения нелинейных уравненийСкачать

Метод Ньютона - отделение корнейСкачать

Комбинированный метод приближенного нахождения корня уравненияСкачать

Метод дихотомииСкачать

Метод хордСкачать

Метод Ньютона (касательных) и хорд Численное решение уравнения c++Скачать

5.1 Численные методы решения уравнений F(x)=0Скачать