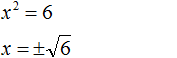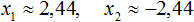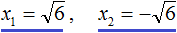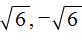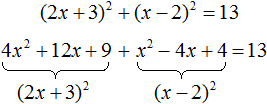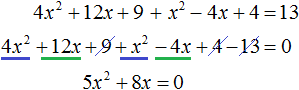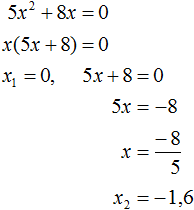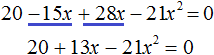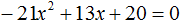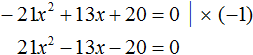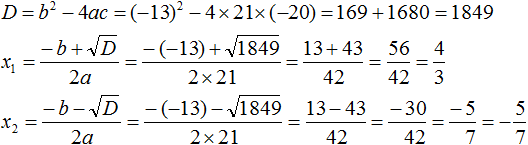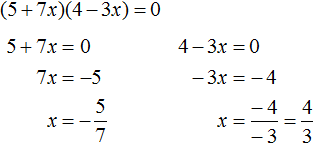Что такое квадратное уравнение? Виды квадратных уравнений. Примеры.
Обычно квадратные уравнения — одна из самых любимых учениками тем школьной математики. Почему? Потому, что алгоритм решения любого квадратного уравнения достаточно прост и универсален. Работает безотказно. Однако простора для дурацких ошибок при решении квадратных уравнений тоже хватает, да… Так что будем разбираться, что к чему.)
Начнём с названия.
Ключевым словом в понятии квадратное уравнение является слово «квадратное». Что оно означает? Оно означает то, что в уравнении обязательно должен присутствовать икс в квадрате. В любом случае. Также в уравнении могут быть (или не быть — как уж повезёт) просто икс (в первой степени) и просто число (свободный член). Но это ещё не всё. При этом в уравнении не должно быть иксов в кубе, в четвёртой и любых других степенях, больших двойки.
В самом общем виде квадратное уравнение выглядит так:
Здесь a, b, c — какие-то числа. Любые.) Числа b и c могут быть совсем-совсем любыми, а вот а — любым числом, кроме нуля. Почему — объясню чуть ниже.
В этих уравнениях слева присутствует полный набор слагаемых: есть икс в квадрате (с коэффициентом a), есть просто икс (с коэффициентом b), а также есть свободный член c. Такие квадратные уравнения в математике так и называются — полными.
А ещё бывают и такие квадратные уравнения, где чего-то не хватает. Что у нас произойдёт, если, например, обнулить коэффициент b (b=0)? У нас исчезнет икс в первой степени.
Получится, к примеру, что-то типа:
А если c=0? Тогда у нас пропадёт свободный член:
А если уж оба коэффициента a и b станут равны нулю, то тогда совсем всё просто получится:
Такие квадратные уравнения, где какого-то из членов не хватает, называются (вы не поверите) неполными.)
Таким образом, квадратные уравнения бывают двух основных видов — полные и неполные.
А теперь ответ на вопрос, почему коэффициент a не может быть равен нулю. А давайте подумаем, что у нас произойдёт, если мы обнулим коэффициент а? Да! У нас пропадёт икс в квадрате! Наше уравнение превратится в линейное . И решаться будет уже совсем по-другому…
Общая формула корней квадратного уравнения.
Квадратные уравнения решаются достаточно просто. По одной единственной универсальной формуле. Всего одной!
И теперь у меня для вас есть две новости — хорошая и плохая. С какой начнём? Принято с плохой начинать? Что ж, ладно…
Новость плохая. Строгий аналитический вывод общей формулы корней квадратного уравнения достаточно громоздок и основан на процедуре выделения полного квадрата. В большинстве школьных учебников вывод общей формулы корней всё-таки приводят, но я считаю что эта процедура — очередной вынос мозга простому среднестатистическому школьнику. Поэтому в данном уроке я его (вывод) всё-таки опущу.)
Новость хорошая. Запоминать аналитический вывод формулы корней квадратного уравнения в общем виде и не требуется. Вообще! Гораздо важнее запомнить саму формулу и научиться её применять на практике. Вот мы и попрактикуемся. И уравнения порешаем.)
«Формула! Где формула?! Ты достал формулу?» — слышу громкие возгласы, как в старом добром рекламном ролике начала 2000-х…
Достаю, достаю! Из широких штанин… О-па! Вот она, формула!)
Вот такая формула. Да, я не спорю, довольно громоздкая. Но и уравнение мы решаем всё-таки квадратное, а не более простое линейное…
Как вы видите, для поиска корней квадратного уравнения нам необходимы только коэффициенты a, b, c. И всё. Больше ничего. Аккуратно подставляем все коэффициенты в формулу и считаем наши корни.
Что такое дискриминант? Формула и смысл дискриминанта.
Выражение b 2 -4ac, стоящее в формуле под знаком квадратного корня, называется дискриминант. До боли знакомое и родное слово для большинства старшеклассников. Слова «решаем через дискриминант» звучат обнадёживающе и вселяют оптимизм!)
Обычно дискриминант обозначается буковкой D:
Тогда, с учётом данного обозначения, общая формула корней станет выглядеть вот так:
Сам по себе дискриминант, как правило, прост и безотказен в обращении. Но… В чём его смысл? Почему для, скажем, —b или 2a не вводятся какие-то специальные термины и обозначения? Буквы — они и в Африке буквы… А тут — такое красивое слово! Дискриминант…
А дело вот в чём. При решении любого квадратного уравнения по общей формуле возможны всего три ситуации.
1. Дискриминант положительный (D>0).
Это означает, что из него можно извлечь корень. Красиво корень извлекается или некрасиво — вопрос другой. Главное, что извлекается в принципе.
Тогда наше квадратное уравнение всегда имеет два различных корня.
Два — потому, что общая формула в этой ситуации разбивается на два отдельных случая. А именно — какой знак, плюс или минус, берётся перед радикалом. Каждый случай даёт свой корень.
2. Дискриминант равен нулю (D=0)
Как вы думаете, чему в этом случае будет равен корень из дискриминанта? Нулю, конечно же! А поскольку от прибавления/вычитания нуля в числителе ничего не меняется, то наше уравнение имеет один корень:
Вообще, строго говоря, это не один корень, а два одинаковых. Но в упрощённом виде, когда нам надо просто решить уравнение и получить ответ, принято говорить об одном решении. Поэтому в ответе не заморачиваются и пишут просто одинокий икс, безо всякой индексации х1,2 .
Однако в более солидных темах (например, в решении неравенств методом интервалов ) этот пунктик, с двумя одинаковыми (или, по-научному, кратными) корнями, настолько важен, что я буду про него напоминать снова и снова.
3. Дискриминант отрицательный (D
Из отрицательных чисел извлекать квадратный корень в средней школе не учат. Это означает, что уравнение не имеет корней. Ну и ладно. На нет, как говорится, и суда нет.
Как решать квадратные уравнения?
Начнём с полных квадратных уравнений.
Полные квадратные уравнения
Полное квадратное уравнение (любое!) решается всегда в четыре основных этапа.
1. Приводим уравнение к стандартному виду:
Всё просто: выстраиваем левую часть уравнения по убыванию степеней икса. На первом месте пишем слагаемое с иксом в квадрате, на втором месте — с иксом в первой степени и, наконец, свободный член. Справа — обязательно должен быть ноль! Если справа тусуются ещё какие-то члены, то переносим их в левую часть и приводим подобные.
Конечно, если уравнение уже дано в стандартном виде, то первый этап делать не нужно.)
Как только уравнение представлено в стандартном виде, приступаем ко второму этапу.
2. Внимательно осматриваем уравнение и определяем (правильно!) коэффициенты a, b и c.
Если опыта пока что мало, во избежание досадных ошибок бывает очень полезным выписать их отдельно.
3. Считаем дискриминант по формуле D = b 2 -4ac.
Внимание! На данном этапе сразу же извлекаем корень из дискриминанта! Если красиво извлекается, конечно.)
4. Подставляем все значения в общую формулу, считаем корни уравнения и записываем ответ.
Вот и весь алгоритм. Простой и безотказный. Ну что, тренируемся на кошках?
Например, надо решить вот такое уравнение:
Работаем прямо по пунктам.
1. Приводим уравнение к стандартному виду.
Уравнение уже дано нам в стандартном виде. Стало быть, уже готово к решению. Слева — полный набор членов, выстроенных по убыванию степеней, а справа — ноль. Посему переходим сразу ко второму этапу.
2. Внимательно осматриваем уравнение и определяем (правильно!) коэффициенты a, b и c.
3. Считаем дискриминант по формуле D = b 2 -4ac.
Аккуратно подставляем наши коэффициенты a, b и с в формулу дискриминанта. Подставляем со своими знаками! Частенько именно в знаках коэффициентов народ и путается. Точнее, не столько в самих знаках, сколько в подстановке отрицательных значений в формулу дискриминанта. Вот и не ленимся, аккуратно пишем все знаки и скобочки. Трудов много не отнимет, зато гарантированно убережёт от досадных промахов:
Извлекаем корень из дискриминанта:
Отлично, корень извлекается чисто. Теперь переходим к последнему, самому главному этапу — считаем наши корни.
4. Подставляем все значения в общую формулу, аккуратно считаем корни уравнения и записываем ответ.
Опять же, аккуратно подставляем все числа в формулу, со всеми знаками и скобочками:
Вот и всё. Это ответ.)
Кстати сказать, если вы просто решаете квадратное уравнение, то нет особой нужды отдельно считать дискриминант. Можно работать напрямую с общей формулой, просто аккуратно подставляя в неё коэффициенты a, b и с.
В нашем случае можно было бы сразу записать:
Но такое оформление чревато тем, что, впопыхах, можно где-нибудь потерять минус. Оно вам надо? Посему лучше считайте дискриминант отдельно — ошибок меньше будет. Естественно, посчитав дискриминант, не забывайте про корень.) Специально акцентирую внимание на этом моменте, потому что сам дискриминант народ обычно считает правильно, а вот корень извлечь частенько забывает… К тому же, привыкнув к отдельному поиску дискриминанта, вы быстрее запомните его общую формулу — в более серьёзных заданиях пригодится. Например, в задачах с параметрами. Такие задачи — высший пилотаж на ЕГЭ!
Естественно, бывают и сюрпризы. Не без этого… И к ним (к сюрпризам) тоже надо быть готовым, да. Чтобы не растеряться, в случае чего…) Рассмотрим первый сюрприз. Самый безобидный.
Например, дано нам такое уравнение:
Как обычно, работаем прямо по алгоритму.
1. Приводим уравнение к стандартному виду.
Уравнение пока не готово к решению. Справа нужен ноль, а у нас справа тусуется 4х. Не беда: переносим 4х влево и выстраиваем члены по убыванию степеней:
2. Внимательно осматриваем уравнение и определяем (правильно!) коэффициенты a, b и c.
3. Считаем дискриминант по формуле D = b 2 -4ac.
А вот и первый сюрприз.) Дискриминант не является точным квадратом целого числа! И корень из дискриминанта извлекается плохо:
Что делать? Не решается уравнение? Ну да, как же!
Ничего страшного.) Работаем прямо с корнем. Естественно, если есть возможность, то выносим всё, что извлекается, за знак корня:
4. Подставляем все значения в общую формулу, аккуратно считаем корни уравнения и записываем ответ.
Корни нашего уравнения получились иррациональными. Ну и ничего страшного. Бывает.) Такой уж пример.
Открою небольшой секрет. Обычно задания на квадратные уравнения составляются так, чтобы корень из дискриминанта извлекался ровно и, тем самым, корни в ответе получались красивыми — либо целыми, либо рациональными. И народ постепенно привыкает к таким простым примерам наивно полагая, что дискриминант всегда обязан получаться точным квадратом. Не обязан! Более того, суровая реальность такова, что некрасивый дискриминант (а вместе с ним и лохматые иррациональные корни) — скорее правило, чем исключение! И если вы захотите задать какое-нибудь квадратное уравнение, выбрав в нём коэффициенты a, b и с случайным образом, то с вероятностью 99% корни вашего квадратного уравнения будут числами иррациональными.
Но иррациональных корней вовсе не надо бояться.) Ибо они — точно такие же числа, как и все остальные. Кстати говоря, в более серьёзных заданиях (неравенствах, задачах с параметрами) иррациональные корни встречаются сплошь и рядом. И с ними надо обязательно уметь работать — сравнивать, изображать на числовой оси и т.д. И мы тоже поработаем! В соответствующих уроках.)
Как видите, процедура решения полных квадратных уравнений проблем не вызывает. Всё просто, быстро, не больно.) Главное — аккуратно подставляйте коэффициенты в формулу дискриминанта и общую формулу корней. И считайте себе.) И что, думаете, ошибиться нельзя? Ну да, как же…
Вот краткий перечень глупых ошибок при решении квадратных уравнений:
1. Путаница в знаках. Ошибки в подстановке отрицательных коэффициентов в формулу дискриминанта и в общую формулу корней .
2. Забывают извлечь корень из дискриминанта.
3. При работе с общей формулой корней в знаменатель дроби частенько подставляется не 2а, как положено, а просто двойка. Привыкает, видите ли, народ к простым уравнениям, с первым коэффициентом единичкой (а=1). Внимательнее надо быть, да.)
Например, дано такое уравнение:
Уравнение, в принципе, уже дано нам в стандартном виде. Слева — квадратный трёхчлен, построенный по убыванию степеней, справа — ноль.
Наши коэффициенты будут:
Можно приступать к решению. Только это… коэффициенты — дробные. Неудобно как-то…
Согласен, неудобно! Всё-таки лучше, когда уравнение безо всяких дробей, в линеечку.) Вот и избавимся сначала от дробей. На что надо домножить обе части уравнения, чтобы и двойка сократилась и тройка? На 6! Вот и домножаем. Слева получим:
А что будет справа? Справа будет ноль. Ноль на что ни умножай — всё равно ноль будет. Хорошее число.)
-2х 2 + 9х — 30 = 0
И опять не бросаемся решать, считать дискриминант и прочее. Минус перед иксом в квадрате — нехорош. Забыть его очень легко. Посему избавимся от этого минуса умножением обеих частей на (-1). Проще говоря, поменяем слева все знаки:
2х 2 — 9х + 30 = 0
Ну вот. А теперь — по накатанной колее. Выписываем коэффициенты:
Вот так штука! А дискриминант-то отрицательный! Не можем мы корень из отрицательного числа извлечь. И сами корни посчитать, стало быть, тоже не можем, да. Стало быть, ответ — решений нет.
Это был второй сюрприз. Надеюсь, теперь отрицательный дискриминант в каком-нибудь примере вас нисколько не смутит.)
Это всё что касается полных квадратных уравнений. Теперь переходим к неполным.)
Неполные квадратные уравнения
Неполными, напоминаю, называются квадратные уравнения, где чего-то не хватает — или bx или с. Или обоих членов сразу.
Неполные квадратные уравнение также можно решать через дискриминант, по общей формуле. Надо только правильно догадаться, чему равняются коэффициенты a, b и с.
Догадались? В первом случае a = 1, b = -3, а свободный член с вообще отсутствует! Что это означает? В математике это означает, что с=0! Вот и всё.)
Во втором уравнении всё аналогично, только нулю будет равно не с, а b!
Но неполные уравнения можно решать гораздо проще. Безо всяких дискриминантов и безо всяких формул! Зачем же из пушки по воробьям…
Например, такое уравнение:
Что здесь можно сделать в левой части? Сильнее всего напрашивается вынести икс за скобки и разложить левую часть на множители. Давайте вынесем:
И что дальше? А то, что произведение равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю! Вот и приравниваем (в уме!) каждый из множителей к нулю и получаем:
И все дела! Это и будут корни нашего уравнения. Оба годятся.) При подстановке каждого из них в исходное уравнение мы получим железное равенство 0=0. Как видите, решение куда проще, чем через дискриминант!
Теперь рассмотрим другое уравнение:
А здесь что можно сделать? Можно -16 перенести вправо:
Остаётся корень извлечь из 16 и — ответ готов:
И так решаются все неполные квадратные уравнения. Либо с помощью вынесения икса за скобки и разложения на множители, либо же переносом свободного члена вправо с последующим извлечением корня. Спутать эти два способа — надо очень хорошо постараться.) Ибо в первом случае вам пришлось бы корень из икса извлекать, что как-то не очень, а во втором случае выносить за скобки нечего…
Подытожим тему практическими советами.
1. Перед решением любого квадратного уравнения приводим его к стандартному виду, выстраиваем левую часть по убыванию степеней.
2. Если в уравнении имеются дробные коэффициенты, избавляемся от дробей умножением всего уравнения на нужный множитель.
3. Если коэффициент перед иксом в квадрате отрицательный, избавляемся от минуса умножением всего уравнения на (-1).
Ну что, наш урок окончен. Теперь можно и порешать.)
- Как решать квадратные уравнения
- Понятие квадратного уравнения
- Приведенные и неприведенные квадратные уравнения
- Полные и неполные квадратные уравнения
- Решение неполных квадратных уравнений
- Как решить уравнение ax 2 = 0
- Как решить уравнение ax 2 + с = 0
- Как решить уравнение ax 2 + bx = 0
- Как разложить квадратное уравнение
- Дискриминант: формула корней квадратного уравнения
- Алгоритм решения квадратных уравнений по формулам корней
- Примеры решения квадратных уравнений
- Формула корней для четных вторых коэффициентов
- Формула Виета
- Упрощаем вид квадратных уравнений
- Связь между корнями и коэффициентами
- Квадратное уравнение
- Что такое квадратное уравнение и как его решать?
- Формулы корней квадратного уравнения
- Примеры решения квадратных уравнений
- Примеры решения задач
- 📹 Видео
Видео:Алгебра 8 класс (Урок№19 - Уравнение х² = а.)Скачать

Как решать квадратные уравнения
О чем эта статья:
Видео:5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

Понятие квадратного уравнения
Уравнение — это равенство, содержащее переменную, значение которой нужно найти.
Например, х + 8 = 12 — это уравнение, которое содержит переменную х.
Корень уравнения — это такое значение переменной, которое при подстановке в уравнение обращает его в верное числовое равенство.
Например, если х = 5, то при подстановке в уравнение мы получим 5 + 8 = 12. 13 = 12 — противоречие. Значит, х = 5 не является корнем уравнения.
А вот если х = 4, то при подстановке в уравнение мы получим 4 + 8 = 12. 12 = 12 — верное равенство. Значит, х = 4 является корнем уравнения.
Решить уравнение — значит найти все его корни или доказать, что их не существует.
Квадратное уравнение — это уравнение вида ax 2 + bx + c = 0, где a — первый или старший коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.
Чтобы запомнить месторасположение коэффициентов, давайте потренируемся определять их.
Квадратные уравнения могут иметь два корня, один корень или не иметь корней.
Чтобы определить, сколько корней имеет уравнение, нужно обратить внимание на дискриминант. Чтобы его найти, берем формулу: D = b 2 − 4ac. А вот свойства дискриминанта:
- если D 0, есть два различных корня.
С этим разобрались. А сейчас посмотрим подробнее на различные виды квадратных уравнений.
Разобраться в теме еще быстрее с помощью опытного преподавателя можно на курсах по математике в онлайн-школе Skysmart.
Видео:Как решать любое квадратное уравнение Полное Неполное квадр ур x^2+2x-3=0 5x^2-2x=0 2x^2-2=0 3x^2=0Скачать

Приведенные и неприведенные квадратные уравнения
Квадратное уравнение может быть приведенным или неприведенным — все зависит от от значения первого коэффициента.
Приведенное квадратное уравнение — это уравнение, где старший коэффициент, тот который стоит при одночлене высшей степени, равен единице.
Неприведенным называют квадратное уравнение, где старший коэффициент отличается от единицы.
Давайте-ка на примерах — вот у нас есть два уравнения:
- x 2 — 2x + 6 = 0
- x 2 — x — 1/4 = 0
В каждом из них старший коэффициент равен единице (которую мы мысленно представляем при x 2 ), а значит уравнение называется приведенным.
- 2x 2 − 4x — 12 = 0 — первый коэффициент отличен от единицы (2), значит это неприведенное квадратное уравнение.
Каждое неприведенное квадратное уравнение можно преобразовать в приведенное, если произвести равносильное преобразование — разделить обе его части на первый коэффициент.
Пример 1. Превратим неприведенное уравнение: 8x 2 + 20x — 9 = 0 — в приведенное.
Для этого разделим обе части исходного уравнения на старший коэффициент 8:
Ответ: равносильное данному приведенное уравнение x 2 + 2,5x — 1,125 = 0.
Видео:Ларинский вариант ЕГЭ №449. Математика на 100 балловСкачать

Полные и неполные квадратные уравнения
В определении квадратного уравнения есть условие: a ≠ 0. Оно нужно, чтобы уравнение ax 2 + bx + c = 0 было именно квадратным. Если a = 0, то уравнение обретет вид линейного: bx + c = 0.
Что касается коэффициентов b и c, то они могут быть равны нулю, как по отдельности, так и вместе. В таком случае квадратное уравнение принято называть неполным.
Неполное квадратное уравнение —— это квадратное уравнение вида ax 2 + bx + c = 0, где оба или хотя бы один из коэффициентов b и c равен нулю.
Полное квадратное уравнение — это уравнение, у которого все коэффициенты отличны от нуля.
| Для самых любопытных объясняем откуда появились такие названия: | |
|---|---|
Такие уравнения отличны от полного квадратного тем, что их левые части не содержат либо слагаемого с неизвестной переменной, либо свободного члена, либо и того и другого. Отсюда и их название — неполные квадратные уравнения. Видео:Решение биквадратных уравнений. 8 класс.Скачать  Решение неполных квадратных уравненийКак мы уже знаем, есть три вида неполных квадратных уравнений:
Давайте рассмотрим по шагам, как решать неполные квадратные уравнения по видам. Как решить уравнение ax 2 = 0Начнем с решения неполных квадратных уравнений, в которых b и c равны нулю, то есть, с уравнений вида ax 2 = 0. Уравнение ax 2 = 0 равносильно x 2 = 0. Такое преобразование возможно, когда мы разделили обе части на некое число a, которое не равно нулю. Корнем уравнения x 2 = 0 является нуль, так как 0 2 = 0. Других корней у этого уравнения нет, что подтверждают свойства степеней. Таким образом, неполное квадратное уравнение ax 2 = 0 имеет единственный корень x = 0. Пример 1. Решить −6x 2 = 0.
Как решить уравнение ax 2 + с = 0Обратим внимание на неполные квадратные уравнения вида ax 2 + c = 0, в которых b = 0, c ≠ 0. Мы давно знаем, что слагаемые в уравнениях носят двусторонние куртки: когда мы переносим их из одной части уравнения в другую, они надевает куртку на другую сторону — меняют знак на противоположный. Еще мы знаем, что если обе части уравнения поделить на одно и то же число (кроме нуля) — у нас получится равносильное уравнение. Ну есть одно и то же, только с другими цифрами. Держим все это в голове и колдуем над неполным квадратным уравнением (производим «равносильные преобразования»): ax 2 + c = 0:
Ну все, теперь мы готовы к выводам о корнях неполного квадратного уравнения. В зависимости от значений a и c, выражение — c/а может быть отрицательным или положительным. Разберем конкретные случаи. Если — c/а 2 = — c/а не имеет корней. Все потому, что квадрат любого числа всегда равен неотрицательному числу. Из этого следует, что при — c/а 0, то корни уравнения x 2 = — c/а будут другими. Например, можно использовать правило квадратного корня и тогда корень уравнения равен числу √- c/а, так как (√- c/а) 2 = — c/а. Кроме того, корнем уравнения может стать -√- c/а, так как (-√- c/а) 2 = — c/а. Ура, больше у этого уравнения нет корней.
Пример 1. Найти решение уравнения 8x 2 + 5 = 0.
Разделим обе части на 8: Ответ: уравнение 8x 2 + 5 = 0 не имеет корней. Как решить уравнение ax 2 + bx = 0Осталось разобрать третий вид неполных квадратных уравнений, когда c = 0. Неполное квадратное уравнение ax 2 + bx = 0 можно решить методом разложения на множители. Как разложить квадратное уравнение: Разложим на множители многочлен, который расположен в левой части уравнения — вынесем за скобки общий множитель x. Теперь можем перейти от исходного уравнения к равносильному x * (ax + b) = 0. А это уравнение равносильно совокупности двух уравнений x = 0 и ax + b = 0, последнее — линейное, его корень x = −b/a. Таким образом, неполное квадратное уравнение ax 2 + bx = 0 имеет два корня: Пример 1. Решить уравнение 0,5x 2 + 0,125x = 0 0,5x = 0,125, Ответ: х = 0 и х = 0,25. Как разложить квадратное уравнениеС помощью теоремы Виета можно получить формулу разложения квадратного трехчлена на множители. Выглядит она так: Формула разложения квадратного трехчлена Если x1 и x2 — корни квадратного трехчлена ax 2 + bx + c, то справедливо равенство ax 2 + bx + c = a (x − x1) (x − x2). Видео:Неполные квадратные уравнения. Алгебра, 8 классСкачать  Дискриминант: формула корней квадратного уравненияЧтобы найти результат квадратного уравнения, придумали формулу корней. Выглядит она так: где D = b 2 − 4ac — дискриминант квадратного уравнения. Эта запись означает: Чтобы легко применять эту формулу, нужно понять, как она получилась. Давайте разбираться. Алгоритм решения квадратных уравнений по формулам корнейТеперь мы знаем, что при решении квадратных уравнения можно использовать универсальную формулу корней — это помогает находить комплексные корни. В 8 классе на алгебре можно встретить задачу по поиску действительных корней квадратного уравнения. Для этого важно перед использованием формул найти дискриминант и убедиться, что он неотрицательный, и только после этого вычислять значения корней. Если дискриминант отрицательный, значит уравнение не имеет действительных корней. Алгоритм решения квадратного уравнения ax 2 + bx + c = 0:
Чтобы запомнить алгоритм решения квадратных уравнений и с легкостью его использовать, давайте тренироваться! Примеры решения квадратных уравненийКак решать квадратные уравнения мы уже знаем, осталось закрепить знания на практике. Пример 1. Решить уравнение −4x 2 + 28x — 49 = 0.
Ответ: единственный корень 3,5. Пример 2. Решить уравнение 54 — 6x 2 = 0.
Оставим неизвестное в одной части, остальное перенесем с противоположным знаком в другую Ответ: два корня 3 и — 3. Пример 3. Решить уравнение x 2 — х = 0.
Ответ: два корня 0 и 1. Пример 4. Решить уравнение x 2 — 10 = 39.
Ответ: два корня 7 и −7. Пример 5. Решить уравнение 3x 2 — 4x+94 = 0.
D = (-4) 2 — 4 * 3 * 94 = 16 — 1128 = −1112 Ответ: корней нет. В школьной программе за 8 класс нет обязательного требования искать комплексные корни, но такой подход может ускорить ход решения. Если дискриминант отрицательный — сразу пишем ответ, что действительных корней нет и не мучаемся. Видео:Математика | Кубические уравнения по методу СталлонеСкачать  Формула корней для четных вторых коэффициентовРассмотрим частный случай. Формула решения корней квадратного уравнения Например, нам нужно решить квадратное уравнение ax 2 + 2nx + c = 0. Сначала найдем его корни по известной нам формуле. Вычислим дискриминант D = (2n) 2 — 4ac = 4n 2 — 4ac = 4(n 2 — ac) и подставим в формулу корней: 2 + 2nx + c = 0″ height=»705″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc11a460e2f8354381151.png» width=»588″> Для удобства вычислений обозначим выражение n 2 -ac как D1. Тогда формула корней квадратного уравнения со вторым коэффициентом 2·n примет вид: где D1 = n 2 — ac. Самые внимательные уже заметили, что D = 4D1, или D1= D/4. Проще говоря, D1 — это четверть дискриминанта. И получается, что знак D1 является индикатором наличия или отсутствия корней квадратного уравнения. Сформулируем правило. Чтобы найти решение квадратного уравнения со вторым коэффициентом 2n, нужно:
Видео:КАК РЕШАТЬ КУБИЧЕСКИЕ УРАВНЕНИЯ | Разбираем на конкретном примереСкачать  Формула ВиетаЕсли в школьной геометрии чаще всего используется теорема Пифагора, то в школьной алгебре ведущую роль занимают формулы Виета. Теорема звучит так: Сумма корней x 2 + bx + c = 0 равна второму коэффициенту с противоположным знаком, а произведение корней равняется свободному члену. Если дано x 2 + bx + c = 0, где x₁ и x₂ являются корнями, то справедливы два равенства: Знак системы, который принято обозначать фигурной скобкой, означает, что значения x₁ и x₂ удовлетворяют обоим равенствам. Рассмотрим теорему Виета на примере: x 2 + 4x + 3 = 0. Пока неизвестно, какие корни имеет данное уравнение. Но в соответствии с теоремой можно записать, что сумма этих корней равна второму коэффициенту с противоположным знаком. Он равен четырем, значит будем использовать минус четыре: Произведение корней по теореме соответствует свободному члену. В данном случае свободным членом является число три. Значит: Необходимо проверить равна ли сумма корней −4, а произведение 3. Для этого найдем корни уравнения x 2 + 4x + 3 = 0. Воспользуемся формулами для чётного второго коэффициента: Получилось, что корнями уравнения являются числа −1 и −3. Их сумма равняется второму коэффициенту с противоположным знаком, а значит решение верное. Произведение корней −1 и −3 по теореме Виета должно равняться свободному члену, то есть числу 3. Это условие также выполняется: Результат проделанных вычислений в том, что мы убедились в справедливости выражения: Когда дана сумма и произведение корней квадратного уравнения, принято начинать подбор подходящих корней. Теорема, обратная теореме Виета, при таких условиях может быть главным помощником. Вот она: Обратная теорема Виета Если числа x1 и x2 таковы, что их сумма равна второму коэффициенту уравнения x 2 + bx + c = 0, взятому с противоположным знаком, а их произведение равно свободному члену, то эти числа и есть корни x 2 + bx + c = 0. Обычно вся суть обратных теорем в том самом выводе, которое дает первая теорема. Так, при доказательстве теоремы Виета стало понятно, что сумма x1 и x2 равна −b, а их произведение равно c. В обратной теореме это и есть утверждение. Пример 1. Решить при помощи теоремы Виета: x 2 − 6x + 8 = 0.
2 − 6x + 8 = 0″ height=»59″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc101ce2e346034751939.png» width=»117″> Когда у нас есть эти два равенства, можно подобрать подходящие корни, которые будут удовлетворять обоим равенствам системы. Чтобы проще подобрать корни, нужно их перемножить. Число 8 можно получить путем перемножения чисел 4 и 2 либо 1 и 8. Но значения x1 и x2 надо подбирать так, чтобы они удовлетворяли и второму равенству тоже. Можно сделать вывод, что значения 1 и 8 не подходят, так как они не удовлетворяют равенству x1 + x2 = 6. А значения 4 и 2 подходят обоим равенствам: Значит числа 4 и 2 — корни уравнения x 2 − 6x + 8 = 0. p> Упрощаем вид квадратных уравненийЕсли мы ходили в школу всегда одной тропинкой, а потом вдруг обнаружили путь короче — это значит теперь у нас есть выбор: упростить себе задачу и сократить время на дорогу или прогуляться по привычному маршруту. Так же и при вычислении корней квадратного уравнения. Ведь проще посчитать уравнение 11x 2 — 4 x — 6 = 0, чем 1100x 2 — 400x — 600 = 0. Часто упрощение вида квадратного уравнения можно получить через умножение или деление обеих частей на некоторое число. Например, в предыдущем абзаце мы упростили уравнение 1100x 2 — 400x — 600 = 0, просто разделив обе части на 100. Такое преобразование возможно, когда коэффициенты не являются взаимно простыми числами. Тогда принято делить обе части уравнения на наибольший общий делитель абсолютных величин его коэффициентов. Покажем, как это работает на примере 12x 2 — 42x + 48 = 0. Найдем наибольший общий делитель абсолютных величин его коэффициентов: НОД (12, 42, 48) = 6. Разделим обе части исходного квадратного уравнения на 6, и придем к равносильному уравнению 2x 2 — 7x + 8 = 0. Вот так просто. А умножение обеих частей квадратного уравнения отлично помогает избавиться от дробных коэффициентов. Умножать в данном случае лучше на наименьшее общее кратное знаменателей его коэффициентов. Например, если обе части квадратного уравнения умножить на НОК (6, 3, 1) = 6, то оно примет более простой вид x 2 + 4x — 18 = 0. Также для удобства вычислений можно избавиться от минуса при старшем коэффициенте квадратного уравнения — для этого умножим или разделим обе части на −1. Например, удобно от квадратного уравнения −2x 2 — 3x + 7 = 0 перейти к решению 2x 2 + 3x — 7 = 0. Связь между корнями и коэффициентамиМы уже запомнили, что формула корней квадратного уравнения выражает корни уравнения через его коэффициенты: Из этой формулы, можно получить другие зависимости между корнями и коэффициентами. Например, можно применить формулы из теоремы Виета: Для приведенного квадратного уравнения сумма корней равна второму коэффициенту с противоположным знаком, а произведение корней — свободному члену. Например, по виду уравнения 3x 2 — 7x + 22 = 0 можно сразу сказать, что сумма его корней равна 7/3, а произведение корней равно 22/3. Можно активно использовать уже записанные формулы и с их помощью получить ряд других связей между корнями и коэффициентами квадратного уравнения. Таким образом можно выразить сумму квадратов корней квадратного уравнения через его коэффициенты: Видео:Математика| Разложение квадратного трехчлена на множители.Скачать  Квадратное уравнениеВидео:ОГЭ №21 Как решать кубическое уравнение x^3+4x^2-9x-36=0 Группировка Деление многочлена столбикомСкачать  Что такое квадратное уравнение и как его решать?Мы помним, что уравнение это равенство, содержащее в себе переменную, значение которой нужно найти. Если переменная, входящая в уравнение, возведенá во вторую степень (в квадрат), то такое уравнение называют уравнением второй степени или квадратным уравнением. Например, следующие уравнения являются квадратными: Решим первое из этих уравнений, а именно x 2 − 4 = 0 . Все тождественные преобразования, которые мы применяли при решении обычных линейных уравнений, можно применять и при решении квадратных. Итак, в уравнении x 2 − 4 = 0 перенесем член −4 из левой части в правую часть, изменив знак: Получили уравнение x 2 = 4 . Ранее мы говорили, что уравнение считается решённым, если в одной части переменная записана в первой степени и её коэффициент равен единице, а другая часть равна какому-нибудь числу. То есть чтобы решить уравнение, его следует привести к виду x = a , где a — корень уравнения. У нас переменная x всё ещё во второй степени, поэтому решение необходимо продолжить. Чтобы решить уравнение x 2 = 4 , нужно ответить на вопрос при каком значении x левая часть станет равна 4 . Очевидно, что при значениях 2 и −2 . Чтобы вывести эти значения воспользуемся определением квадратного корня. Число b называется квадратным корнем из числа a , если b 2 = a и обозначается как У нас сейчас похожая ситуация. Ведь, что такое x 2 = 4 ? Переменная x в данном случае это квадратный корень из числа 4, поскольку вторая степень x прирáвнена к 4. Тогда можно записать, что Обычно записывают так: перед квадратным корнем ставят знак «плюс-минус», затем находят арифметическое значение квадратного корня. В нашем случае на этапе когда записано выражение Затем найти арифметическое значение квадратного корня Выражение x = ± 2 означает, что x = 2 и x = −2 . То есть корнями уравнения x 2 − 4 = 0 являются числа 2 и −2 . Запишем полностью решение данного уравнения: Выполним проверку. Подставим корни 2 и −2 в исходное уравнение и выполним соответствующие вычисления. Если при значениях 2 и −2 левая часть равна нулю, то это будет означать, что уравнение решено верно: В обоих случаях левая часть равна нулю. Значит уравнение решено верно. Решим ещё одно уравнение. Пусть требуется решить квадратное уравнение (x + 2) 2 = 25 Для начала проанализируем данное уравнение. Левая часть возведенá в квадрат и она равна 25 . Какое число в квадрате равно 25 ? Очевидно, что числа 5 и −5 То есть наша задача найти x, при которых выражение x + 2 будет равно числам 5 и −5 . Запишем эти два уравнения: Решим оба уравнения. Это обычные линейные уравнения, которые решаются легко: Значит корнями уравнения (x + 2) 2 = 25 являются числа 3 и −7 . В данном примере как и в прошлом можно использовать определение квадратного корня. Так, в уравнения (x + 2) 2 = 25 выражение (x + 2) представляет собой квадратный корень из числа 25 . Поэтому можно cначала записать, что Тогда правая часть станет равна ±5 . Полýчится два уравнения: x + 2 = 5 и x + 2 = −5. Решив по отдельности каждое из этих уравнений мы придём к корням 3 и −7 . Запишем полностью решение уравнения (x + 2) 2 = 25 Из рассмотренных примеров видно, что квадратное уравнение имеет два корня. Чтобы не забыть о найденных корнях, переменную x можно подписывать нижними индексами. Так, корень 3 можно обозначить через x1 , а корень −7 через x2 В предыдущем примере тоже можно было сделать так. Уравнение x 2 − 4 = 0 имело корни 2 и −2 . Эти корни можно было обозначить как x1 = 2 и x2 = −2. Бывает и так, что квадратное уравнение имеет только один корень или вовсе не имеет корней. Такие уравнения мы рассмотрим позже. Сделаем проверку для уравнения (x + 2) 2 = 25 . Подставим в него корни 3 и −7 . Если при значениях 3 и −7 левая часть равна 25 , то это будет означать, что уравнение решено верно: В обоих случаях левая часть равна 25 . Значит уравнение решено верно. Квадратное уравнение бывает дано в разном виде. Наиболее его распространенная форма выглядит так: ax 2 + bx + c = 0 , Это так называемый общий вид квадратного уравнения. В таком уравнении все члены собраны в общем месте (в одной части), а другая часть равна нулю. По другому такой вид уравнения называют нормальным видом квадратного уравнения. Пусть дано уравнение 3x 2 + 2x = 16 . В нём переменная x возведенá во вторую степень, значит уравнение является квадратным. Приведём данное уравнение к общему виду. Итак, нам нужно получить уравнение, которое будет похоже на уравнение ax 2 + bx + c = 0 . Для этого в уравнении 3x 2 + 2x = 16 перенесем 16 из правой части в левую часть, изменив знак: Получили уравнение 3x 2 + 2x − 16 = 0 . В этом уравнении a = 3 , b = 2 , c = −16 . В квадратном уравнении вида ax 2 + bx + c = 0 числа a , b и c имеют собственные названия. Так, число a называют первым или старшим коэффициентом; число b называют вторым коэффициентом; число c называют свободным членом. В нашем случае для уравнения 3x 2 + 2x − 16 = 0 первым или старшим коэффициентом является 3 ; вторым коэффициентом является число 2 ; свободным членом является число −16 . Есть ещё другое общее название для чисел a, b и c — параметры. Так, в уравнении 3x 2 + 2x − 16 = 0 параметрами являются числа 3 , 2 и −16 . В квадратном уравнении желательно упорядочивать члены так, чтобы они располагались в таком же порядке как у нормального вида квадратного уравнения. Например, если дано уравнение −5 + 4x 2 + x = 0 , то его желательно записать в нормальном виде, то есть в виде ax 2 + bx + c = 0. В уравнении −5 + 4x 2 + x = 0 видно, что свободным членом является −5 , он должен располагаться в конце левой части. Член 4x 2 содержит старший коэффициент, он должен располагаться первым. Член x соответственно будет располагаться вторым: Квадратное уравнение в зависимости от случая может принимать различный вид. Всё зависит от того, чему равны значения a , b и с . Если коэффициенты a , b и c не равны нулю, то квадратное уравнение называют полным. Например, полным является квадратное уравнение 2x 2 + 6x − 8 = 0 . Если какой-то из коэффициентов равен нулю (то есть отсутствует), то уравнение значительно уменьшается и принимает более простой вид. Такое квадратное уравнение называют неполным. Например, неполным является квадратное уравнение 2x 2 + 6x = 0, в нём имеются коэффициенты a и b (числа 2 и 6 ), но отсутствует свободный член c. Рассмотрим каждый из этих видов уравнений, и для каждого из этих видов определим свой способ решения. Пусть дано квадратное уравнение 2x 2 + 6x − 8 = 0 . В этом уравнении a = 2 , b = 6 , c = −8 . Если b сделать равным нулю, то уравнение примет вид: Получилось уравнение 2x 2 − 8 = 0 . Чтобы его решить перенесем −8 в правую часть, изменив знак: Для дальнейшего упрощения уравнения воспользуемся ранее изученными тождественными преобразованиями. В данном случае можно разделить обе части на 2 У нас получилось уравнение, которое мы решали в начале данного урока. Чтобы решить уравнение x 2 = 4 , следует воспользоваться определением квадратного корня. Если x 2 = 4 , то Значит корнями уравнения 2x 2 − 8 = 0 являются числа 2 и −2 . Запишем полностью решение данного уравнения: Выполним проверку. Подставим корни 2 и −2 в исходное уравнение и выполним соответствующие вычисления. Если при значениях 2 и −2 левая часть равна нулю, то это будет означать, что уравнение решено верно: В обоих случаях левая часть равна нулю, значит уравнение решено верно. Уравнение, которое мы сейчас решили, является неполным квадратным уравнением. Название говорит само за себя. Если полное квадратное уравнение выглядит как ax 2 + bx + c = 0 , то сделав коэффициент b нулём получится неполное квадратное уравнение ax 2 + c = 0 . У нас тоже сначала было полное квадратное уравнение 2x 2 + 6x − 4 = 0 . Но мы сделали коэффициент b нулем, то есть вместо числа 6 поставили 0 . В результате уравнение обратилось в неполное квадратное уравнение 2x 2 − 4 = 0 . В начале данного урока мы решили квадратное уравнение x 2 − 4 = 0 . Оно тоже является уравнением вида ax 2 + c = 0 , то есть неполным. В нем a = 1 , b = 0 , с = −4 . Также, неполным будет квадратное уравнение, если коэффициент c равен нулю. Рассмотрим полное квадратное уравнение 2x 2 + 6x − 4 = 0 . Сделаем коэффициент c нулём. То есть вместо числа 4 поставим 0 Получили квадратное уравнение 2x 2 + 6x=0 , которое является неполным. Чтобы решить такое уравнение, переменную x выносят за скобки: Получилось уравнение x(2x + 6) = 0 в котором нужно найти x, при котором левая часть станет равна нулю. Заметим, что в этом уравнении выражения x и (2x + 6) являются сомножителями. Одно из свойств умножения говорит, что произведение равно нулю, если хотя бы один из сомножителей равен нулю (или первый сомножитель или второй). В нашем случае равенство будет достигаться, если x будет равно нулю или (2x + 6) будет равно нулю. Так и запишем для начала: Получилось два уравнения: x = 0 и 2x + 6 = 0 . Первое уравнение решать не нужно — оно уже решено. То есть первый корень равен нулю. Чтобы найти второй корень, решим уравнение 2x + 6 = 0 . Это обычное линейное уравнение, которое решается легко: Видим, что второй корень равен −3. Значит корнями уравнения 2x 2 + 6x = 0 являются числа 0 и −3 . Запишем полностью решение данного уравнения: Выполним проверку. Подставим корни 0 и −3 в исходное уравнение и выполним соответствующие вычисления. Если при значениях 0 и −3 левая часть равна нулю, то это будет означать, что уравнение решено верно: Следующий случай это когда числа b и с равны нулю. Рассмотрим полное квадратное уравнение 2x 2 + 6x − 4 = 0 . Сделаем коэффициенты b и c нулями. Тогда уравнение примет вид: Получили уравнение 2x 2 = 0 . Левая часть является произведением, а правая часть равна нулю. Произведение равно нулю, если хотя бы один из сомножителей равен нулю. Очевидно, что x = 0 . Действительно, 2 × 0 2 = 0 . Отсюда, 0 = 0 . При других значениях x равенства достигаться не будет. Проще говоря, если в квадратном уравнении вида ax 2 + bx + c = 0 числа b и с равны нулю, то корень такого уравнения равен нулю. Отметим, что когда употребляются словосочетания « b равно нулю » или « с равно нулю «, то подразумевается, что параметры b или c вовсе отсутствуют в уравнении. Например, если дано уравнение 2x 2 − 32 = 0 , то мы говорим, что b = 0 . Потому что если сравнить с полным уравнением ax 2 + bx + c = 0 , то можно заметить, что в уравнении 2x 2 − 32 = 0 присутствует старший коэффициент a , равный 2; присутствует свободный член −32 ; но отсутствует коэффициент b . Наконец, рассмотрим полное квадратное уравнение ax 2 + bx + c = 0 . В качестве примера решим квадратное уравнение x 2 − 2x + 1 = 0 . Итак, требуется найти x , при котором левая часть станет равна нулю. Воспользуемся изученными ранее тождественными преобразованиями. Прежде всего заметим, что левая часть уравнения представляет собой квадрат разности двух выражений. Если мы вспомним как раскладывать многочлен на множители, то получим в левой части (x − 1) 2 . Рассуждаем дальше. Левая часть возведенá в квадрат и она равна нулю. Какое число в квадрате равно нулю? Очевидно, что только 0 . Поэтому наша задача найти x , при котором выражение x − 1 равно нулю. Решив простейшее уравнение x − 1 = 0 , можно узнать чему равно x Этот же результат можно получить, если воспользоваться квадратным корнем. В уравнении (x − 1) 2 = 0 выражение (x − 1) представляет собой квадратный корень из нуля. Тогда можно записать, что Значит корнем уравнения x 2 − 2x + 1 = 0 является единица. Других корней у данного уравнения нет. В данном случае мы решили квадратное уравнение, имеющее только один корень. Такое тоже бывает. Не всегда бывают даны простые уравнения. Рассмотрим например уравнение x 2 + 2x − 3 = 0 . В данном случае левая часть уже не является квадратом суммы или разности. Поэтому нужно искать другие пути решения. Заметим, что левая часть уравнения представляет собой квадратный трехчлен. Тогда можно попробовать выделить полный квадрат из этого трёхчлена и посмотреть что это нам даст. Выделим полный квадрат из квадратного трёхчлена, располагающего в левой части уравнения: В получившемся уравнении перенесем −4 в правую часть, изменив знак: Теперь воспользуемся квадратным корнем. В уравнении (x + 1) 2 = 4 выражение (x + 1) представляет собой квадратный корень из числа 4 . Тогда можно записать, что Значит корнями уравнения x 2 + 2x − 3 = 0 являются числа 1 и −3 . Пример 3. Решить уравнение x 2 − 6x + 9 = 0 , выделив полный квадрат. Выделим полный квадрат из левой части: Далее воспользуемся квадратным корнем и узнáем чему равно x Значит корнем уравнения x 2 − 6x + 9 = 0 является 3. Выполним проверку: Пример 4. Решить квадратное уравнение 4x 2 + 28x − 72 = 0 , выделив полный квадрат: Выделим полный квадрат из левой части: Перенесём −121 из левой части в правую часть, изменив знак: Воспользуемся квадратным корнем: Получили два простых уравнения: 2x + 7 = 11 и 2x + 7 = −11. Решим их: Пример 5. Решить уравнение 2x 2 + 3x − 27 = 0 Это уравнение немного посложнее. Когда мы выделяем полный квадрат, первый член квадратного трёхчлена мы представляем в виде квадрата какого-нибудь выражения. Так, в прошлом примере первым членом уравнения был 4x 2 . Его можно было представить в виде квадрата выражения 2x , то есть (2x) 2 = 2 2 x 2 = 4x 2 . Чтобы убедиться что это правильно, можно извлечь квадратный корень из выражения 4x 2 . Это квадратный корень из произведения — он равен произведению корней: В уравнении 2x 2 + 3x − 27 = 0 первый член это 2x 2 . Его нельзя представить в виде квадрата какого-нибудь выражения. Потому что нет числá, квадрат которого равен 2. Если бы такое число было, то этим числом был бы квадратный корень из числа 2. Но квадратный корень из числа 2 извлекается только приближённо. А приближённое значение не годится для представления числá 2 в виде квадрата. Если обе части исходного уравнения умножить или разделить на одно и то же число, то полýчится уравнение равносильное исходному. Это правило сохраняется и для квадратного уравнения. Тогда можно разделить обе части нашего уравнения на 2 . Это позвóлит избавиться от двойки перед x 2 что впоследствии даст нам возможность выделить полный квадрат: Перепишем левую часть в виде трёх дробей со знаменателем 2 Сократим первую дробь на 2. Остальные члены левой части перепишем без изменений. Правая часть по-прежнему станет равна нулю: Выделим полный квадрат. При представлении члена Свернём полученный полный квадрат: Приведём подобные члены: Перенесём дробь Воспользуемся квадратным корнем. Выражение Для вычисления правой части воспользуемся правилом извлечения квадратного корня из дроби: Тогда наше уравнение примет вид: Полýчим два уравнения: Значит корнями уравнения 2x 2 + 3x − 27 = 0 являются числа 3 и Корень Выполним проверку. Подставим найденные корни в исходное уравнение: В обоих случаях левая часть равна нулю, значит уравнение 2x 2 + 3x − 27 = 0 решено верно. Решая уравнение 2x 2 + 3x − 27 = 0 , в самом начале мы разделили обе его части на 2 . В результате получили квадратное уравнение, в котором коэффициент перед x 2 равен единице: Такой вид квадратного уравнения называют приведённым квадратным уравнением. Любое квадратное уравнение вида ax 2 + bx + c = 0 можно сделать приведённым. Для этого нужно разделить обе его части на коэффициент, который располагается перед x². В данном случае обе части уравнения ax 2 + bx + c = 0 нужно разделить на a Пример 6. Решить квадратное уравнение 2x 2 + x + 2 = 0 Сделаем данное уравнение приведённым: Выделим полный квадрат: Получили уравнение Следовательно, нет такого значения x , при котором левая часть стала бы равна А поскольку уравнение Видео:Свойства квадратного корня. Уравнение х2=а, 8 классСкачать  Формулы корней квадратного уравненияВыделять полный квадрат для каждого решаемого квадратного уравнения не очень удобно. Можно ли создать универсальные формулы для решения квадратных уравнений? Оказывается можно. Сейчас мы этим и займёмся. Взяв за основу буквенное уравнение ax 2 + bx + c = 0 , и выполнив некоторые тождественные преобразования, мы сможем получить формулы для вывода корней квадратного уравнения ax 2 + bx + c = 0 . В эти формулы можно будет подставлять коэффициенты a , b , с и получать готовые решения. Итак, выделим полный квадрат из левой части уравнения ax 2 + bx + c = 0. Сначала сделаем данное уравнение приведённым. Разделим обе его части на a Теперь в получившемся уравнении выделим полный квадрат: Перенесем члены Приведём правую часть к общему знаменателю. Дроби, состоящие из букв, привóдят к общему знаменателю методом «крест-нáкрест». То есть знаменатель первой дроби станóвится дополнительным множителем второй дроби, а знаменатель второй дроби станóвится дополнительным множителем первой дроби: В числителе правой части вынесем за скобки a Сократим правую часть на a Поскольку все преобразования были тождественными, то получившееся уравнение Уравнение Поскольку при любом a не рáвным нулю, знаменатель правой части уравнения Выражение b 2 − 4ac называют дискриминантом квадратного уравнения. Дискриминант это латинское слово, означающее различитель . Дискриминант квадратного уравнения обозначается через букву D Дискриминант позволяет заранее узнать имеет ли уравнение корни или нет. Так, в предыдущем задании мы долго решали уравнение 2x 2 + x + 2 = 0 и оказалось, что оно не имеет корней. Дискриминант же позволил бы нам заранее узнать, что корней нет. В уравнении 2x 2 + x + 2 = 0 коэффициенты a , b и c равны 2, 1 и 2 соответственно. Подставим их в формулу D = b 2 −4ac D = b 2 − 4ac = 1 2 − 4 × 2 × 2 = 1 − 16 = −15. Видим, что D (оно же b 2 − 4ac ) является отрицательным числом. Тогда нет смысла решать уравнение 2x 2 + x + 2 = 0, выделяя в нём полный квадрат, потому что когда мы дойдем до уравнения вида Станóвится понятно почему древние люди считали выражение b 2 − 4ac различителем. Это выражение подобно индикатору позволяет различить уравнение имеющего корни от уравнения, не имеющего корней. Итак, D равно b 2 − 4ac . Подставим в уравнении Если дискриминант исходного уравнения окажется меньше нуля (D , то уравнение примет вид: В этом случае говорят, что у исходного уравнения корней нет, поскольку квадрат любого числа не должен быть отрицательным. Если дискриминант исходного уравнения окажется больше нуля (D > 0) , то уравнение примет вид: В этом случае уравнение будет иметь два корня. Для их вывода воспользуемся квадратным корнем: Получили уравнение Получившиеся два равенства это и есть универсальные формулы для решения квадратного уравнения ax 2 + bx + c = 0. Их называют формулами корней квадратного уравнения . Чаще всего эти формулы обозначаются как x1 и x2 . То есть для вычисления первого корня используется формула c индексом 1; для вывода второго корня — формула с индексом 2. Обозначим свои формулы так же: Очерёдность применения формул не важнá. Решим например квадратное уравнение x 2 + 2x − 8 = 0 с помощью формул корней квадратного уравнения. Коэффициенты данного квадратного уравнения это числа 1 , 2 и −8 . То есть, a = 1 , b = 2 , c = −8 . Прежде чем использовать формулы корней квадратного уравнения, нужно найти дискриминант этого уравнения. Найдём дискриминант квадратного уравнения. Для этого воспользуемся формулой D = b 2 − 4 ac . Вместо переменных a, b и c у нас будут коэффициенты уравнения x 2 + 2x − 8 = 0 D = b 2 − 4ac = 2 2 − 4 × 1 × (−8) = 4 + 32 = 36 Дискриминант больше нуля. Значит уравнение имеет два корня. Теперь можно воспользоваться формулами корней квадратного уравнения: Значит корнями уравнения x 2 + 2x − 8 = 0 являются числа 2 и −4 . Проверкой убеждаемся, что корни найдены верно: Наконец, рассмотрим случай когда дискриминант квадратного уравнения равен нулю. Вернёмся к уравнению И в этом случае квадратное уравнение будет иметь только один корень. Воспользуемся квадратным корнем: Далее выражаем x Это ещё одна формула для вывода корня квадратного корня. Рассмотрим её применение. Ранее мы решили уравнение x 2 − 6x + 9 = 0 , имеющее один корень 3. Решили мы его методом выделения полного квадрата. Теперь попробуем решить с помощью формул. Найдём дискриминант квадратного уравнения. В этом уравнении a = 1 , b = −6 , c = 9 . Тогда по формуле дискриминанта имеем: D = b 2 − 4ac = (−6) 2 − 4 × 1 × 9 = 36 − 36 = 0 Дискриминант равен нулю (D = 0) . Это означает, что уравнение имеет только один корень, и вычисляется он по формуле Значит корнем уравнения x 2 − 6x + 9 = 0 является число 3. Для квадратного уравнения, имеющего один корень также применимы формулы Применим эти две формулы для предыдущего уравнения. В обоих случаях получим один и тот же ответ 3 Если квадратное уравнение имеет только один корень, то желательно применять формулу Пример 3. Решить уравнение 5x 2 − 6x + 1 = 0 Найдём дискриминант квадратного уравнения: Дискриминант больше нуля. Значит уравнение имеет два корня. Воспользуемся формулами корней квадратного уравнения: Значит корнями уравнения 5x 2 − 6x + 1 = 0 являются числа 1 и Ответ: 1; Пример 4. Решить уравнение x 2 + 4x + 4 = 0 Найдём дискриминант квадратного уравнения: Дискриминант равен нулю. Значит уравнение имеет только один корень. Он вычисляется по формуле Значит корнем уравнения x 2 + 4x + 4 = 0 является число −2 . Пример 5. Решить уравнение 3x 2 + 2x + 4 = 0 Найдём дискриминант квадратного уравнения: Дискриминант меньше нуля. Значит корней у данного уравнения нет. Ответ: корней нет. Пример 6. Решить уравнение (x + 4) 2 = 3x + 40 Приведём данное уравнение к нормальному виду. В левой части располагается квадрата суммы двух выражений. Раскрóем его: Перенесём все члены из правой части в левую часть, изменив их знаки. В правой части останется ноль: Приведём подобные члены в левой части: В получившемся уравнении найдём дискриминант: Дискриминант больше нуля. Значит уравнение имеет два корня. Воспользуемся формулами корней квадратного уравнения: Значит корнями уравнения (x + 4) 2 = 3x + 40 являются числа 3 и −8 . Ответ: 3 ; −8. Пример 7. Решить уравнение Умнóжим обе части данного уравнения на 2 . Это позвóлит нам избавиться от дроби в левой части: В получившемся уравнении перенесём 22 из правой части в левую часть, изменив знак. В правой части останется 0 Приведём подобные члены в левой части: В получившемся уравнении найдём дискриминант: Дискриминант больше нуля. Значит уравнение имеет два корня. Воспользуемся формулами корней квадратного уравнения: Значит корнями уравнения Ответ: 23; −1. Пример 8. Решить уравнение Умнóжим обе части на наименьшее общее кратное знаменателей обеих дробей. Это позвóлит избавиться от дробей в обеих частях. Наименьшее общее кратное чисел 2 и 3 это число 6 . Тогда получим: В получившемся уравнении раскроем скобки в обеих частях: Теперь перенесём все члены из правой части в левую часть, изменив у них знаки. В правой части останется 0 Приведём подобные члены в левой части: В получившемся уравнении найдём дискриминант: Дискриминант больше нуля. Значит уравнение имеет два корня. Воспользуемся формулами корней квадратного уравнения: Значит корнями уравнения Видео:8 класс. Квадратные уравнения. x2=aСкачать  Примеры решения квадратных уравненийПример 1. Решить уравнение x 2 = 81 Это простейшее квадратное уравнение, в котором надо определить число, квадрат которого равен 81. Таковыми являются числа 9 и −9. Воспользуемся квадратным корнем для их вывода: Ответ: 9, −9 . Пример 2. Решить уравнение x 2 − 9 = 0 Это неполное квадратное уравнение. Для его решения нужно перенести член −9 в правую часть, изменив знак. Тогда получим: Ответ: 3, −3. Пример 3. Решить уравнение x 2 − 9x = 0 Это неполное квадратное уравнение. Для его решения сначала нужно вынести x за скобки: Левая часть уравнения является произведением. Произведение равно нулю, если хотя один из сомножителей равен нулю. Левая часть станет равна нулю, если отдельно x равно нулю, или если выражение x − 9 равно нулю. Получится два уравнения, одно из которых уже решено: Ответ: 0, 9 . Пример 4. Решить уравнение x 2 + 4x − 5 = 0 Это полное квадратное уравнение. Его можно решить методом выделения полного квадрата или с помощью формул корней квадратного уравнения. Решим данное уравнение с помощью формул. Сначала найдём дискриминант: D = b 2 − 4ac = 4 2 − 4 × 1 × (−5) = 16 + 20 = 36 Дискриминант больше нуля. Значит уравнение имеет два корня. Вычислим их: Ответ: 1, −5 . Пример 5. Решить уравнение Умнóжим обе части на наименьшее общее кратное чисел 5, 3 и 6. Это позвóлит избавиться от дробей в обеих частях: В получившемся уравнении перенесём все члены из правой части в левую часть, изменив знак. В правой части останется ноль: Приведём подобные члены: Решим получившееся уравнение с помощью формул: Ответ: 5 , Пример 6. Решить уравнение x 2 = 6 В данном примере как и в первом нужно воспользоваться квадратным корнем: Однако, квадратный корень из числа 6 не извлекается. Он извлекается только приближённо. Корень можно извлечь с определённой точностью. Извлечём его с точностью до сотых: Но чаще всего корень оставляют в виде радикала: Ответ: Пример 7. Решить уравнение (2x + 3) 2 + (x − 2) 2 = 13 Раскроем скобки в левой части уравнения: В получившемся уравнении перенесём 13 из правой части в левую часть, изменив знак. Затем приведём подобные члены: Получили неполное квадратное уравнение. Решим его: Ответ: 0 , −1,6 . Пример 8. Решить уравнение (5 + 7x)(4 − 3x) = 0 Данное уравнение можно решить двумя способами. Рассмотрим каждый из них. Первый способ. Раскрыть скобки и получить нормальный вид квадратного уравнения. Приведём подобные члены: Перепишем получившееся уравнение так, чтобы член со старшим коэффициентом располагался первым, член со вторым коэффициентом — вторым, а свободный член располагался третьим: Чтобы старший член стал положительным, умнóжим обе части уравнения на −1. Тогда все члены уравнения поменяют свои знаки на противоположные: Решим получившееся уравнение с помощью формул корней квадратного уравнения: Второй способ. Найти значения x , при которых сомножители левой части уравнения равны нулю. Этот способ удобнее и намного короче. Произведение равно нулю, если хотя бы один из сомножителей равен нулю. В данном случае равенство в уравнении (5 + 7x)(4 − 3x) = 0 будет достигаться, если выражение (5 + 7x) равно нулю, или же выражение (4 − 3x) равно нулю. Наша задача выяснить при каких x это происходит: Видео:Решение квадратных уравнений. Дискриминант. 8 класс.Скачать  Примеры решения задачПредстáвим, что возникла необходимость построить небольшую комнату, площадь которой 8 м 2 . При этом длина комнаты должна быть в два раза больше её ширины. Как определить длину и ширину такой комнаты? Сделаем примерный рисунок этой комнаты, который иллюстрирует вид сверху: Обозначим ширину комнаты через x . А длину комнаты через 2x , потому что по условию задачи длина должна быть в два раза больше ширины. Множитель 2 и выполнит это требование: Поверхность комнаты (её пол) является прямоугольником. Для вычисления площади прямоугольника, нужно длину данного прямоугольника умножить на его ширину. Сделаем это: По условию задачи площадь должна быть 8 м 2 . Значит выражение 2x × x следует приравнять к 8 Получилось уравнение. Если решить его, то можно найти длину и ширину комнаты. Первое что можно сделать это выполнить умножение в левой части уравнения: В результате этого преобразования переменная x перешла во вторую степень. А мы говорили, что если переменная, входящая в уравнение, возведенá во вторую степень (в квадрат), то такое уравнение является уравнением второй степени или квадратным уравнением. Для решения нашего квадратного уравнения воспользуемся изученными ранее тождественными преобразованиями. В данном случае можно разделить обе части на 2 Теперь воспользуемся квадратным корнем. Если x 2 = 4 , то Через x была обозначена ширина комнаты. Ширина не должна быть отрицательной, поэтому в расчёт берём только значение 2 . Такое часто бывает при решении задачи, в которых применяется квадратное уравнение. В ответе получаются два корня, но условию задачи удовлетворяет только один из них. А длина была обозначена через 2x . Значение x теперь известно, подставим его в выражение 2x и вычислим длину: Значит длина равна 4 м , а ширина 2 м . Это решение удовлетворяет условию задачи, поскольку площадь комнаты равна 8 м 2 Ответ: длина комнаты составляет 4 м , а ширина 2 м . Пример 2. Огородный участок, имеющий форму прямоугольника, одна сторона которого на 10 м больше другой, требуется обнести изгородью. Определить длину изгороди, если известно, что площадь участка равна 1200 м 2 Решение Длина прямоугольника, как правило, больше его ширины. Пусть ширина участка x метров, а длина (x + 10) метров. Площадь участка составляет 1200 м 2 . Умножим длину участка на его ширину и приравняем к 1200 , получим уравнение: Решим данное уравнение. Для начала раскроем скобки в левой части: Перенесём 1200 из правой части в левую часть, изменив знак. В правой части останется 0 Решим получившееся уравнение с помощью формул: Несмотря на то, что квадратное уравнение имеет два корня, в расчёт берём только значение 30 . Потому что ширина не может выражаться отрицательным числом. Итак, через x была обозначена ширина участка. Она равна тридцати метрам. А длина была обозначена через выражение x + 10 . Подставим в него найденное значение x и вычислим длину: x + 10 = 30 + 10 = 40 м Значит длина участка составляет сорок метров, а ширина тридцать метров. Эти значения удовлетворяют условию задачи, поскольку если перемножить длину и ширину (числа 40 и 30 ) получится 1200 м 2 40 × 30 = 1200 м 2 Теперь ответим на вопрос задачи. Какова длина изгороди? Чтобы её вычислить нужно найти периметр участка. Периметр прямоугольника это сумма всех его сторон. Тогда: P = 2(a + b) = 2 × (40 + 30) = 2 × 70 = 140 м. Ответ: длина изгороди огородного участка составляет 140 м. 📹 ВидеоРешите уравнение x^2+3x=54. | ОГЭ 2017 | ЗАДАНИЕ 4 | ШКОЛА ПИФАГОРАСкачать  №1 Квадратное уравнение х^2+x-6=0 Дискриминант, теорема ВиетаСкачать  №2 Квадратное уравнение со скобками (х-1)(x-2)=-6х Как избавиться от скобок в уравнении Как решить уСкачать  Быстрый способ решения квадратного уравненияСкачать  Алгебра 8. Урок 9 - Квадратные уравнения. Полные и неполныеСкачать  Сложные уравнения. Как решить сложное уравнение?Скачать  Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать  |
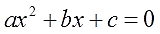
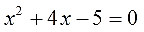
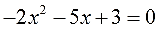
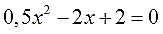
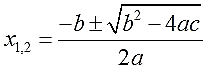
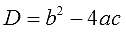
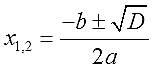

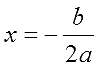
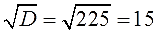
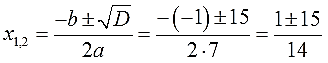
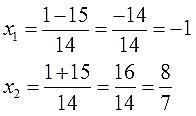
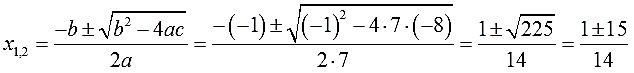
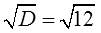
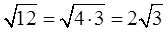
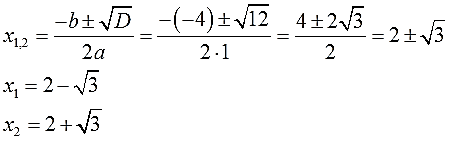
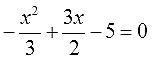
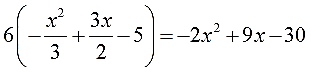
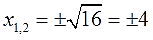








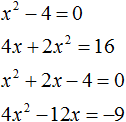
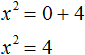
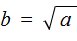
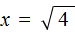 . Вычисление правой части позвóлит узнать чему равно x . Квадратный корень имеет два значения: положительное и отрицательное. Тогда получаем x = 2 и x = −2 .
. Вычисление правой части позвóлит узнать чему равно x . Квадратный корень имеет два значения: положительное и отрицательное. Тогда получаем x = 2 и x = −2 .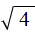 следует поставить знак ±
следует поставить знак ±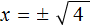
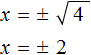
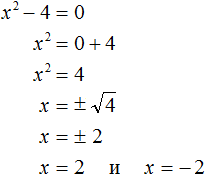
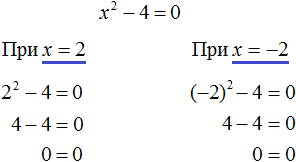


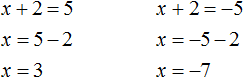
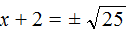 .
.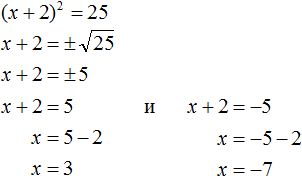

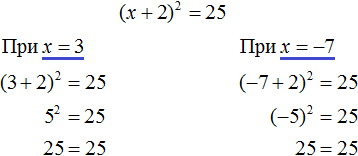
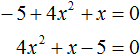
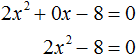
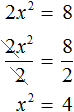
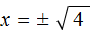 . Отсюда x = 2 и x = −2 .
. Отсюда x = 2 и x = −2 .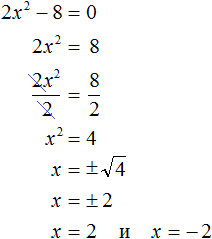
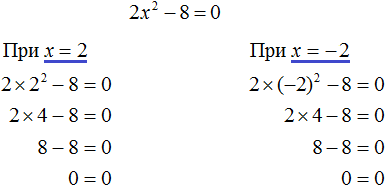
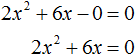
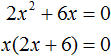

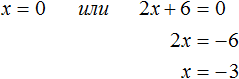
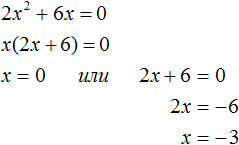
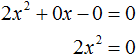
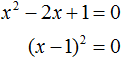
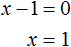
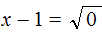 . В этом примере записывать перед корнем знак ± не нужно, поскольку корень из нуля имеет только одно значение — ноль. Тогда получается x − 1 = 0 . Отсюда x = 1 .
. В этом примере записывать перед корнем знак ± не нужно, поскольку корень из нуля имеет только одно значение — ноль. Тогда получается x − 1 = 0 . Отсюда x = 1 .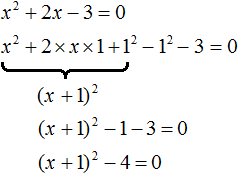
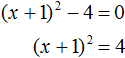
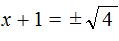 . Вычисление правой части даст выражение x + 1 = ±2 . Отсюда полýчится два уравнения: x + 1 = 2 и x + 1 = −2 , корнями которых являются числа 1 и −3
. Вычисление правой части даст выражение x + 1 = ±2 . Отсюда полýчится два уравнения: x + 1 = 2 и x + 1 = −2 , корнями которых являются числа 1 и −3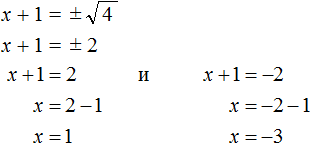

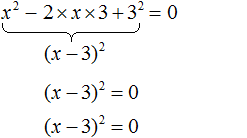
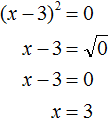
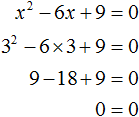
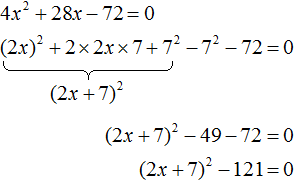
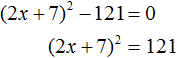
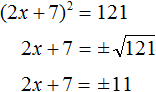

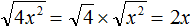
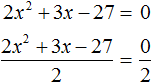
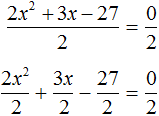
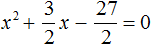
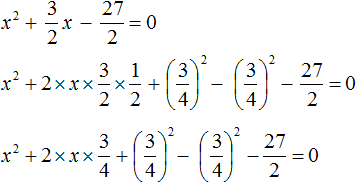
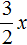 в виде удвоенного произведения, появление множителя 2 привело бы к тому, что этот множитель и знаменатель дроби
в виде удвоенного произведения, появление множителя 2 привело бы к тому, что этот множитель и знаменатель дроби  сократились бы. Чтобы этого не произошло, удвоенное произведение было домножено на
сократились бы. Чтобы этого не произошло, удвоенное произведение было домножено на  . При выделении полного квадрата всегда нужно стараться сделать так, чтобы значение изначального выражения не изменилось.
. При выделении полного квадрата всегда нужно стараться сделать так, чтобы значение изначального выражения не изменилось.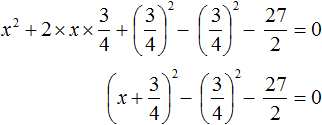
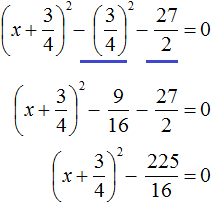
 в правую часть, изменив знак:
в правую часть, изменив знак: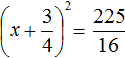
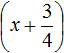 представляет собой квадратный корень из числа
представляет собой квадратный корень из числа 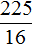
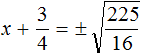

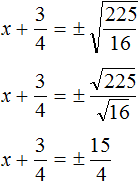
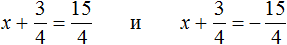
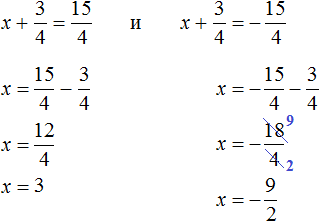
 .
.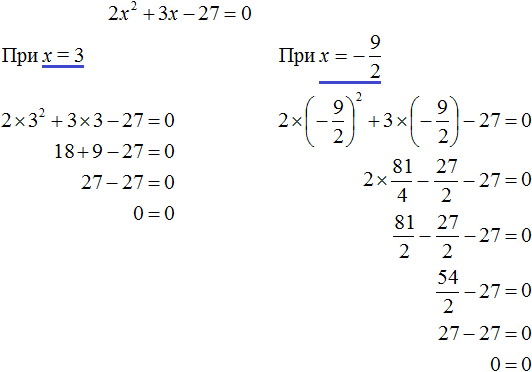

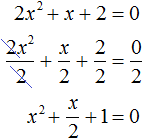
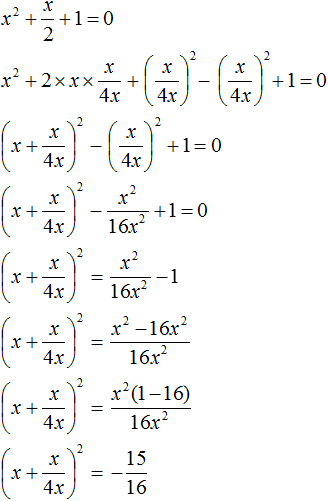
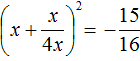 , в котором квадрат выражения
, в котором квадрат выражения  равен отрицательному числу
равен отрицательному числу 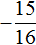 . Такого быть не может, поскольку квадрат любого числа или выражения всегда положителен.
. Такого быть не может, поскольку квадрат любого числа или выражения всегда положителен.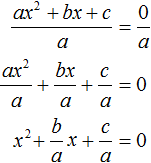
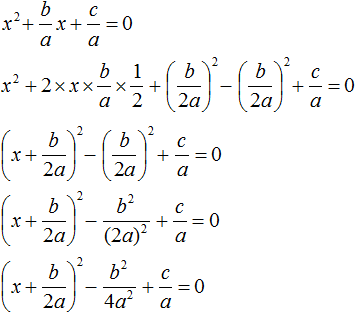
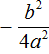 и
и  в правую часть, изменив знак:
в правую часть, изменив знак: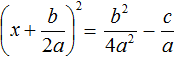
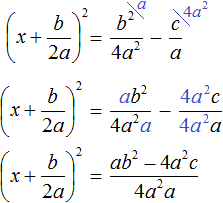
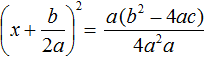
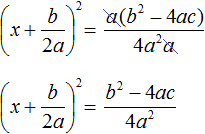
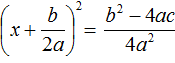 имеет те же корни, что и исходное уравнение ax 2 + bx + c = 0.
имеет те же корни, что и исходное уравнение ax 2 + bx + c = 0.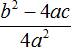 будет зависеть от знака её числителя, то есть от выражения b 2 − 4ac .
будет зависеть от знака её числителя, то есть от выражения b 2 − 4ac .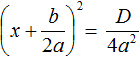
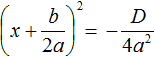
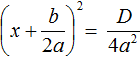
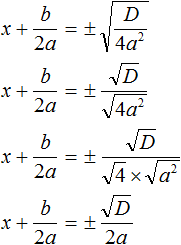
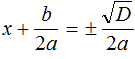 . Из него полýчится два уравнения:
. Из него полýчится два уравнения: 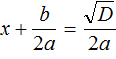 и
и 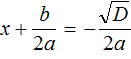 . Выразим x в каждом из уравнений:
. Выразим x в каждом из уравнений: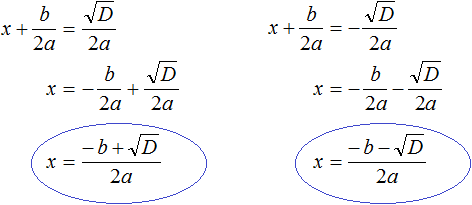

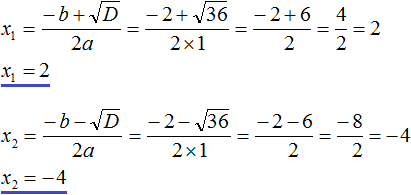
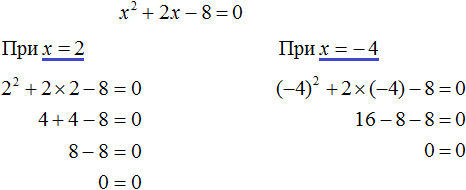
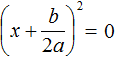
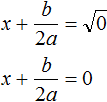
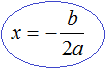
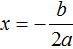
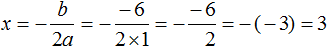
 и
и  . Но применение каждой из них будет давать один и тот же результат.
. Но применение каждой из них будет давать один и тот же результат.
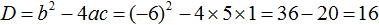
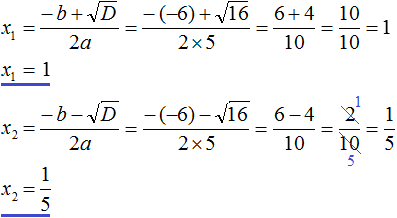
 .
.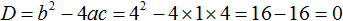
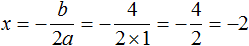
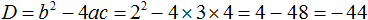
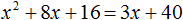
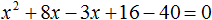
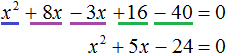
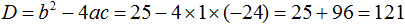
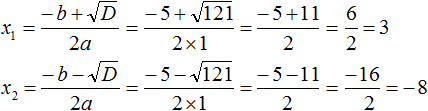
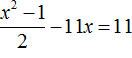
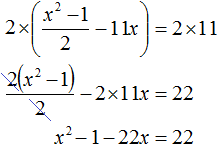
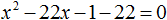
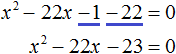
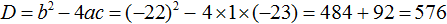
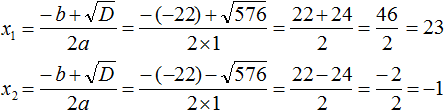
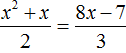
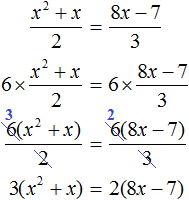
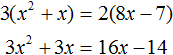
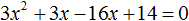
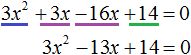
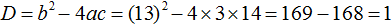
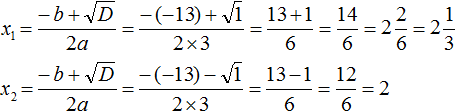
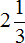 и 2.
и 2.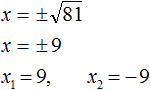
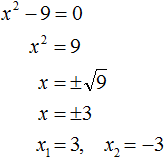
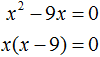
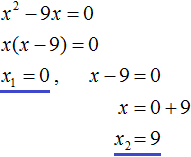
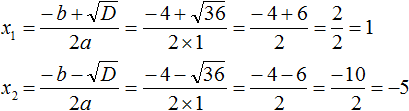
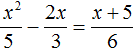
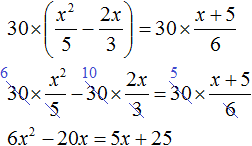
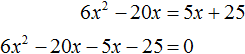
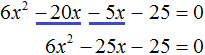
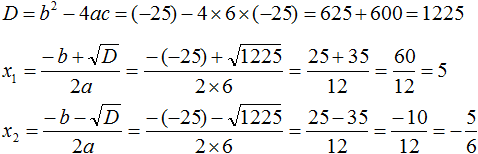
 .
.