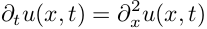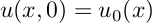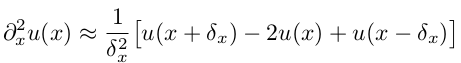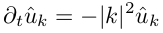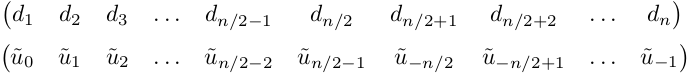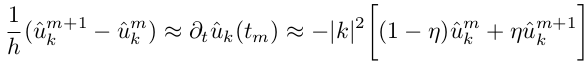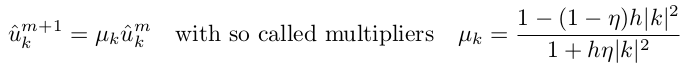Энергетическое неравенство для волнового уравнения (7 видео)

Уравнения математической физики (стр. 5 )

Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5

Тема 8. Задача Коши для волнового уравнения. Энергетическое неравенство. Характеристический конус. Теорема единственности и непрерывной зависимости решений от начальных данных. Волновое уравнение; характеристики; конус Монжа; теорема единственности и непрерывной зависимости решений от начальных данных, её следствия; область единственности решения задачи Коши для волнового уравнения.

Тема 9. Строго гиперболические линейные системы уравнений в частных производных. Симметрические t-гиперболические по Фридрихсу системы первого порядка. Интеграл энергии для звуковых волн. Постановка начальных и смешанных задач для симметрических t-гиперболических систем уравнений первого прядка. Уравнение и неравенство Гамильтона-Якоби. Уравнения акустики. Определения гиперболичности по Петровскому и по Фридрихсу; Строгая гиперболичность линейных систем УЧП; симметрические t-гиперболические по Фридрихсу системы первого порядка; уравнения распространения звуковых волн; интеграл энергии для уравнений акустики; корректная постановка смешанных задач для симметрических t-гиперболических систем первого порядка; характеристические поферхности; уравнение и неравенство Гамильтона-Якоби; неотрицательность квадратичной формы в области единственности решения задачи Коши для уравнений акустики.

Тема 10. Формула Кирхгофа решения задачи Коши для волнового уравнения в R. Распространение колебаний в R. Передний и задний фронт волны. Вывод формулы Киргофа для решения задачи Коши в пространстве; бегущие волны; передний и задний волновой фронт.

Тема 11. Метод спуска. Формула Пуассона решения задачи Коши для волнового уравнения в R. Распространение волн в R и R. Область зависимости решений от начальных данных. Метод спуска; вывод формулы Пуассона решения задачи Коши для волнового уравнения на плоскости; распространение волн на плоскости и на прямой; определение области зависимости решения от начальных данных.

Тема 12. Вывод уравнения теплопроводности. Физический смысл краевых условий. Смешанная краевая задача. Принцип максимума в цилиндре. Теорема единственности и непрерывной зависимости решения первой краевой задачи от начальных и граничных условий. Вывод уравнения теплопроводности из физической постановки задачи; описание физического смысла краевых условий; смешанная краевая задача; принцип максимума в цилиндре; теорема единственности и непрерывной зависимости решения первой краевой задачи от начальных и граничных условий.

Тема 13. Постановка задачи Коши для уравнения теплопроводности. Теорема единственности в классе ограниченных в слое функций. Постановка и примеры задач Коши для уравнения теплопроводности; поиск решения в классе ограниченных в слое функций и теорема единственности для таких решений.

Тема 14. Решение задачи Коши для уравнения теплопроводности при помощи преобразования Фурье. Обоснование формулы Пуассона в случае произвольной ограниченной непрерывной начальной функции. Гладкость решения. Теорема о непрерывной зависимости решения задачи Коши от начальных данных. Теорема Тихонова. Применение преобразований Фурье к УЧП; решение задачи Коши для уравнения теплопроводности с использованием интегральных преобразований Фурье; вывод и обоснование формулы Пуассона в случае произвольной ограниченной непрерывной начальной функции; исследование гладкости решения; теорема о непрерывной зависимости решения задачи Коши от начальных данных; Теорема Тихонова; Следствия к теоремам

Тема 15. Решение смешанной краевой задачи для уравнения теплопроводности в случае одной пространственной переменной методом Фурье. Обоснование метода Фурье для задачи с нулевыми граничными условиями. Гладкость решения. Применение метода Фурье к решению смешанной задачи для одномерного уравнения теплопроводности, при однородных и неоднородных краевых условиях; обоснование метода Фурье для задачи с нулевыми граничными условиями; гладкость решения смешанной задачи для уравнения теплопроводности.

Тема 16. Постановка смешанной задачи с диссипативными граничными условиями. Получение оценок решения и производных для линейных строго гиперболических систем первого порядка. Понятие об обратимых задачах. Понятие диссипативности граничных условий; построение оценок решения и производных для линейных строго гиперболических систем УЧП первого порядка; необходимые условия разрешимости строго гиперболических систем УЧП первого порядка «назад» по времени.

Тема 17. Описание разностной схемы и разностных граничных условий. Оценка разностных отношений и компактность приближенных решений для симметрических гиперболических (по Фридрихсу) систем. Теорема существования решения смешанной задачи. Разностные схемы краевых задач для гиперболических (по Фридрихсу) систем УЧП первого порядка; оценки разностных отношений и компактность приближенных решений для таких систем; теорема существования решения смешанной задачи (с доказательством).

Тема 18. Формулы Грина. Фундаментальное решение уравнения Лапласа. Представление функции в виде суммы трех потенциалов. Интегральные формулы Грина и их обобщение для линейных сопряженных дифференциальных операторов; фундаментальное решение уравнения Лапласа; формула (Грина) интегрального представления дважды непрерывно дифференцируемой в области Функции с использованием сингулярного решения уравнения Лапласа.

Тема 19. Гармонические функции, их свойства (теорема о потоке, о бесконечной дифференцируемости). Принцип максимума. Лемма о нормальной производной. Гармонические функции; теорема о потоке; поведение гармонических функций в ограниченной и бесконечной областях; теорема о среднем; принцип максимума; лемма о нормальной производной.

Тема 20. Основные краевые задачи для уравнения Лапласа. Единственность решения задачи Дирихле в ограниченной области, условие существования решения задачи Неймана. Основные краевые задачи для уравнения Лапласа; единственность решения задачи Коши для уравнения Лапласа в ограниченной области; условие существования решения задачи Неймана для уравнения Лапласа.

Тема 21. Постановка внешних краевых задач Дирихле и Неймана. Исследование единственности. Постановка внешних краевых задач Дирихле и Неймана (для уравнения Лапласа); исследование единственности их решения; примеры постановок с решениями.

Тема 22. Функция Грина задачи Дирихле для уравнения Лапласа, ее симметрия. Функция Грина шара в Rn. Обоснование формулы Пуассона. Поняитие функции источника задачи Дирихле для уравнения Лапласа; её свойства; построение функции Грина методом отражений для простых областей; функция Грина для шара в n-мерном пространстве; обоснование формулы Пуассона.

Тема 23. Теорема об устранимой особенности для гармонических функций. Неравенство Харнака. Теорема Леувилля. Устранение особенности для гармонических функций; наравенство Харнака; теорема Леувилля; следствия из данных теорем.

Тема 24. Оценки производных гармонических функций. Теорема Лиувилля. Аналитичность гармонических функций. Разложение в ряд гармонических функций; система уравнений Коши-Римана; теорема Леувилля (обобщение).

Тема 25. Обобщенные производные в смысле Соболева. Пространство , его полнота. Обобщенные функции; пространство интегрируемых в квадрате функций; финитные функции; производные регулярно заданных обобщенных функций; Пространство .

Тема 26. Пространство . Неравенство Фридрихса. Нормы и скалярное произведение в и . Пространство Соболева ; вывод неравенства Фридрихса; определения и свойства нормы и скалярного произведения в и .

Тема 27. Обобщенная задача Дирихле для уравнения Пуассона с однородными краевыми условиями. Постановка и исследование обобщеной задачи Дирихле для уравнения Пуассона в предположении однородности краевых условий; условия на бесконечности.

Тема 28. Решение задачи Дирихле для уравнения Пуассона вариационными методом. Описание основных принципов и определений вариационного исчисления применительно к уравнениям математической физики; решение задачи Дирихле для уравнения Лапласа, используя вариационные методы.

Тема 29. Обобщенная задача Дирихле для уравнения Лапласа с неоднородными краевыми условиями. Постановка и исследование обобщенной задачи Дирихле для уравнения Лапласа с неоднородными краевыми условиями.

Тема 30. Оператор усреднения и его свойства. Теоремы о сходимости последовательностей гармонических функций. Обобщенные гармонические функции, их регулярность. Определение и свойства оператора усреднения; ядро интегрального оператора усреднения; теоремы о сходимости последовательности гармонических функций; построение обобщенных гармонических функций; дельта-функция; регулярность обобщенных гармонических функций.

Тема 31. Общее понятие корректной задачи математической физики. Примеры корректных и некорректных задач. Пример Адамара. Рассмотрение понятия корректности постановок различных задач математической физики (для эллиптических, гиперболических и параболических уравнений), его обобщение; пример Адамара.

6. Планы практических занятий.

Тема 1. Задача Коши для квазилинейного уравнения в частных производных первого порядка. Классические и обобщенные решения. (3 часа)

1) Основные определения в уравнениях математической физики.;

2) линейные и квазилинейные уравнения в частных производных первого порядка;

3) первый интеграл;

Тема 2. Физические задачи, приводящие к уравнениям в частных производных второго порядка: уравнение колебаний струны, уравнение теплопроводности. Постановка краевых задач. (3 часа)

1) Описание малых колебаний бесконечной нерастяжимой однородной струны; линейное одномерное уравнение теплопроводности; телеграфное уравнение;

Видео:Шапошникова Т. А. - Уравнения с частными производными - Обобщенные решения волнового уравненияСкачать

2) уравнения Лапласа и Пуассона на плоскости; первая, вторая и третья краевые задачи.

Тема 3. Линейное уравнение с частными производными второго порядка. Приведение линейного уравнения к каноническому виду в точке. Классификация линейных уравнений второго порядка. (2 часа)

1) Определение вида линейного УЧП второго порядка;

2) приведение к каноническому виду в двумерном и многомерном случаях.

Тема 4. Понятие характеристики для линейного уравнения второго порядка. Постановка задачи Коши. Теорема Коши-Ковалевской. Доказательство существования решения. (2 часа)

1) поиск характеристик для линейного УЧП второго порядка; постановка задачи Коши для УЧП второго порядка;

2) применение теоремы Коши-Ковалевской.

Тема 5. Задача Коши для уравнения струны, формула Даламбера. Гладкость решения в зависимости от гладкости начальных данных. Полуограниченная струна, методы четного и нечетного продолжения, условия согласования. (2 часа)

1) решение задачи Коши для уравнения Даламбера; поиск условий гладкости решения.

2) применение метода характеристик применительно к задаче о колебаниях полубесконечной струны.

Тема 6. Ограниченная струна. Метод Фурье. Обоснование метода Фурье для уравнения колебаний закрепленной струны. (2 часа)

1) применение метода Фурье к задаче о малых колебаниях ограниченной струны в отсутствие внешних сил;

2) применение метода Фурье к задаче о малых колебаниях ограниченной струны под действием внешних сил.

Тема 7. Задача Штурма-Лиувилля. Свойства собственных значений и собственных функций оператора Штурма-Лиувилля. Функция Грина задачи Штурма-Лиувилля. Доказательство полноты системы собственных функций сведением к теореме Гильберта-Шмидта. (4 часа)

1) решение задач Штурма-Леувилля; поиск собственных функций и собственные значений оператора Штурма-Леувилля;

2) применение теоремы Гильберта-Шмидта.

построение области единственности и непрерывной зависимости решения волнового уравнения от начальных данных,

1) поиск характеристик и условий на характеристиках для симметрических t-гиперболические по Фридрихсу систем первого порядка;

2) нахождение инвариантов Римана; корректная постановка смешанных задач для симметрических t-гиперболических систем первого порядка;

Тема 10. Формула Кирхгофа решения задачи Коши для волнового уравнения в R. Распространение колебаний в R. Передний и задний фронт волны. (2 часа)

1) применение формулы Кирхгофа;

2) исследование волнового фронта.

Метод спуска для нахождения решения задачи Коши волнового уравнения на плоскости.

Применение принципа максимума в цилиндре при решении смешанной задачи для уравнения теплопроводности.

Тема 13. Постановка задачи Коши для уравнения теплопроводности. Теорема единственности в классе ограниченных в слое функций. (2 часа)

Поиск решения в классе ограниченных в слое функций.

Видео:Метод Фурье для волнового уравненияСкачать

Решение задачи Коши для уравнения теплопроводности с использованием интегральных преобразований Фурье

Применение метода Фурье к решению смешанной задачи для одномерного уравнения теплопроводности, при однородных и неоднородных краевых условиях.

Построение оценок решения и производных для линейных строго гиперболических систем УЧП первого порядка.

Исследование разностные схем краевых задач для гиперболических (по Фридрихсу) систем УЧП первого порядка.

Тема 18. Формулы Грина. Фундаментальное решение уравнения Лапласа. Представление функции в виде суммы трех потенциалов. (3 часа)

Построение интегрального представления дважды непрерывно дифференцируемой в области Функции с использованием сингулярного решения уравнения Лапласа для уравнений различных типов.

Тема 19. Гармонические функции, их свойства (теорема о потоке, о бесконечной дифференцируемости). Принцип максимума. Лемма о нормальной производной. (3 часа)

1) Исследование поведения гармонических функций в ограниченной и бесконечной областях;

2) Применение теоремы о среднем, принципа максимума и лемма о нормальной производной.

Тема 20. Основные краевые задачи для уравнения Лапласа. Единственность решения задачи Дирихле в ограниченной области, условие существования решения задачи Неймана. (2 часа)

Исследование на практике основных краевые задачи для уравнения Лапласа.

Тема 21. Постановка внешних краевых задач Дирихле и Неймана. Исследование единственности. (3 часа)

1) Постановка внешних краевых задач Дирихле и Неймана (для уравнения Лапласа);

2) исследование единственности их решения.

Тема 22. Функция Грина задачи Дирихле для уравнения Лапласа, ее симметрия. Функция Грина шара в Rn. Обоснование формулы Пуассона. (3 часа)

1) построение функции Грина, решая соответствующую ей краевую задачу, для круга и полупространства;

2) построение функции Грина задачи дирихле для уравнения Лапласа методом отражений для простых областей.

Тема 23. Теорема об устранимой особенности для гармонических функций. Неравенство Харнака. Теорема Леувилля. (2 часа)

Применение наравенства Харнака и теоремы Леувилля.

Тема 24. Оценки производных гармонических функций. Теорема Лиувилля. Аналитичность гармонических функций. (2 часа)

Разложение в ряд гармонических функций.

Тема 25. Обобщенные производные в смысле Соболева. Пространство , его полнота. (2 часа)

Вычисление производных регулярно заданных обобщенных функций.

Тема 26. Пространство . Неравенство Фридрихса. Нормы и скалярное произведение в и . (2 часа)

Исследование задач и их решений в пространстве Соболева .

Тема 27. Обобщенная задача Дирихле для уравнения Пуассона с однородными краевыми условиями. (2 часа)

Постановка и исследование обобщеной задачи Дирихле для уравнения Пуассона в предположении однородности краевых условий

Тема 28. Решение задачи Дирихле для уравнения Пуассона вариационными методом. (2 часа)

Решение задачи Дирихле для уравнения Лапласа, используя вариационные методы.

Видео:Шапошникова Т. А. - Уравнения с частными производными - Волновые уравненияСкачать

Тема 29. Обобщенная задача Дирихле для уравнения Лапласа с неоднородными краевыми условиями. (2 часа)

Постановка и исследование обобщенной задачи Дирихле для уравнения Лапласа с неоднородными краевыми условиями.

Тема 30. Оператор усреднения и его свойства. Теоремы о сходимости последовательностей гармонических функций. Обобщенные гармонические функции, их регулярность. (2 часа)

Применение оператора усреднения; построение обобщенных гармонических функций.

Тема 31. Общее понятие корректной задачи математической физики. Примеры корректных и некорректных задач. Пример Адамара. (2 часа)

Проверка корректности постановок различных задач математической физики.

· Постановка задачи Коши для систем уравнений гиперболического типа.

· Построение обобщенных решений для строго гиперболических систем.

· Построение численных схем для строго гиперболических систем уравнений.

· Применение функции источника для построения решений задач о распространении тепла.

· Применение метода граничных интегральных уравнений для решения задач математической физики.

· Решение некоторых краевых задач для уравнения Лапласа с использованием их интегральных представлений.

8. Учебно-методическое обеспечение самостоятельной работы студентов. Оценочные средства для текущего контроля успеваемости, промежуточной аттестации по итогам освоения дисциплины (модуля).

В течение семестра студенты решают задачи, указанные преподавателем, к каждому семинару. В каждом семестре проводятся по 2 контрольные работы. Зачет выставляется после решения всех задач контрольных работ. Ниже приведен пример контрольных работ по семестрам.

Контрольная работа № 1

1. В каждой области, где сохраняется тип уравнения, привести его к каноническому виду: .

2. Найти общее решение уравнения: , и решить задачу Коши с начальными условиями: , .

3. Решить задачу: , , , , , , .

Контрольная работа № 2

1. Решить задачу: , , , , , .

2. Привести к каноническому виду систему:
,
где , , и матрицы имеют вид: , , .

3. Решить задачу Коши: , , , .

Контрольная работа № 3

1. Решить краевую задачу Дирихле для уравнения Лапласа в кольце с центром в начале координат , с граничными условиями: , .

2. Для заданной функции вычислить
,
где ― некоторая точка из .

3. Построить функцию Грина для полуполосы .

Контрольная работа № 4

1. Найти потенциал электростатического поля, создаваемого точечным зарядом внутри заземленной сферы.

2. Найти логарифмический потенциал двойного слоя отрезка с постоянной плотностью моментов.

3. С помощью потенциала двойного слоя решить задачу Дирихле:
, , .

8.2. Примерные вопросы для подготовки к экзамену.

1) Задача Коши для квазилинейного уравнения в частных производных первого порядка.

2) Классификация линейных уравнений второго порядка.

3) Гармонические функции, их свойства.

4) Задача Коши для уравнения струны, формула Даламбера.

5) Метод Фурье для начально-краевых задач.

6) Обобщение метода Фурье.

7) Свойства собственных значений и собственных функций оператора Штурма-Лиувилля.

8) Задача Коши для волнового уравнения.

9) Постановка начальных и смешанных задач для симметриических t-гиперболических систем уравнений первого прядка.

10) Формула Кирхгофа решения задачи Коши для волнового уравнения в R.

Видео:Волновая функция (видео 5) | Квантовая физика | ФизикаСкачать

11) Постановка задачи Коши для уравнения теплопроводности. Теорема единственности в классе ограниченных в слое функций.

12) Решение задачи Коши для уравнения теплопроводности при помощи преобразования Фурье.

13) Постановка смешанной задачи с диссипативными граничными условиями.

14) Оценка разностных отношений и компактность приближенных решений для симметрических гиперболических (по Фридрихсу) систем.

15) Формулы Грина. Представление функции в виде суммы трех потенциалов.

16) Гармонические функции, их свойства.

17) Единственность решения задачи Дирихле в ограниченной области, условие существования решения задачи Неймана для уравнения Лапласа.

18) Неравенство Фридрихса.

19) Обобщенная задача Дирихле для уравнения Пуассона с однородными краевыми условиями.

20) Теоремы о сходимости последовательностей гармонических функций.

21) Общее понятие корректной задачи математической физики.

9. Образовательные технологии.

При изучении дисциплины «Уравнения математической физики» используются следующие образовательные технологии:

– аудиторные занятия (лекционные и практические занятия);

– внеаудиторные занятия (самостоятельная работа, индивидуальные консультации).

В соответствии с требованиями ФГОС при реализации различных видов учебной работы в процессе изучения дисциплины «Уравнения математической физики» предусматривается использование в учебном процессе следующих активных и интерактивных форм проведения занятий:

– работа в малых группах по темам, изучаемым на практических занятиях.

10.1. Основная литература:

1) «Уравнения математической физики». М.: Наука, 1979.

2) «Лекции по уравнениям в частных производных». М.: Изд-во иностр. литературы, 1957.

3) , , «Уравнения в частных производных математической физики». М.: Изд-во Высшая школа, 1970.

4) «Лекции об уравнениях с частными производными». М.: Физматгиз, 1961.

5) , «Уравнения математической физики». М.: Изд-во Моск. Ун-та, 1999.

6) «Сборник задач по уравнениям математической физики». М.: Физматлит, 2001

7) , «Уравнения математической физики» (учеб. пособие). Тюмень: Изд-во Тюменского гос. ун-та, 2004.

10.2. Дополнительная литература:

8) . «Лекции об уравнениях с частными производными». М.: Фазис, 1997.

9) , , «Сборник задач по математической физике». М.: Наука, 1972, 4-е изд. М.: Физматлит, 2003.

10) C. «Уравнения математической физики». М.: Наука, 1988.

Видео:Задача Коши для волнового уравнения (Часть 1)Скачать

11) «Справочник по дифференциальным уравнениям в частных производных» первого порядка. М.: Наука, 1966.

12) «Уравнения с частными производными». Перевод с англ. М.: Мир, 1964.

13) «Краевые задачи математической физики». М.: Наука, 1973.

14) «Уравнения второго порядка эллиптического и параболического типов». М.: Наука, 1971.

15) «Дифференциальные уравнения в частных производных», М.: Наука, 1983.

16) Смирнов по уравнениям математической физики. М.: Наука, 1968.

17) Соболев математической физики. М.: Наука, 1966.

10.3. Программное обеспечение и Интернет–ресурсы

1) Электронная библиотека Попечительского совета механико-математического факультета Московского государственного университета http://lib. *****

2) eLIBRARY – Научная электронная библиотека (Москва) http://*****

11. Технические средства и материально-техническое обеспечение дисциплины (модуля).

Учебные аудитории для проведения лекционных и практических занятий.

Содержание

Спектральный метод на примере простых задач матфизики
Одномерная задача распространения тепла по стержню
Двумерное уравнение диффузии
Двумерное волновое уравнение
Выводы
🎬 Видео

Спектральный метод на примере простых задач матфизики

В этой статье описан псевдоспектральный метод численного решения уравнений матфизики, используемый в вычислительной гидродинамике, геофизике, климатологии и во многих других областях.

Одномерная задача распространения тепла по стержню

Для начала рассмотрим простую одномерную задачу распространения тепла в стержне. Уравнение, описывающее распространение тепла при некотором начальном распределении температуры по стержню:

Такое уравнение решается аналитически методом разделения переменных, например здесь, но нас интересует как это можно сделать численно. Прежде всего нужно определиться, как считать вторую пространственную производную по х. Проще всего это делается каким-нибудь разностным методом, например:

Но мы поступим иначе. Распределение температуры есть функция координаты и времени, и в каждый момент времени эта функция может быть представлена в виде суммы ряда Фурье, который в численном виде обрезается на n-ом члене:

Где u^«с крышечкой» — это коэффициенты разложения ряда Фурье. Подставим выражение для ряда в уравнение переноса тепла:

Получаем уравнение для коэффициентов Фурье, в котором отсутствует производная по координате! Теперь это обыкновенное дифференциальное уравнение, а не в частных производных, которое можно решить простым разностным методом. Уже легче, теперь остается найти коэффициенты разложения и в этом нам очень поможет быстрое преобразование Фурье (дальше FFT).

Логика здесь следующая:

1) в начальный момент времени дана функция координаты, описывающая распределение температуры по стержню;
2) разбиваем стержень на сетку из n точек;
3) находим комплексные коэффициенты Фурье с помощью алгоритма FFT, обозначим операцию как F(u);
4) умножаем полученные коэффиценты на -|k| 2 , получаем Фурье-образ второй производной. Аналогично можно получить Фурье-образ производной более высоких порядков p, достаточно умножить на (ik) p ;
5) делаем обратное преобразование Фурье F -1 (u), с помощью алгоритма IFFT, получаем значения второй производной в точках на сетке;
6) делаем шаг по времени, уже обычной разностной, явной или неявной, схемой;
7) повторяем.

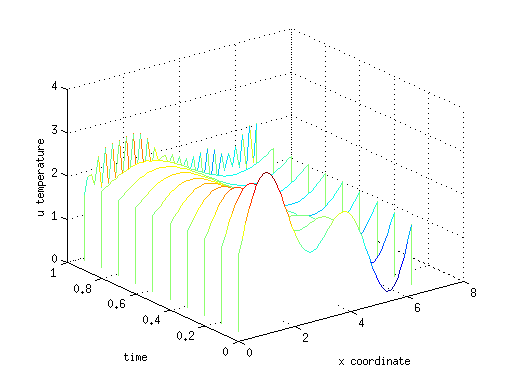
Рассмотрим теперь как это работает в программе для Matlab/Octave. В качестве начального распределения температуры возьмем гладкую функцию u0=2+sin(x)+sin(2x), стержень длинной 2π разобьем на 50 точек, с шагом по времени h=0.1, граничные условия периодичные (кольцо).

Стоит отметить особенность алгоритма FFT в Matlab, связанную с тем, что полученные коэффициенты разложения на выходе d=fft(u) идут не по порядку, а смещены, первая половина на месте второй и наоборот. Cначала идут коэффициенты с номерами от 0 до n/2-1, потом с номерами от -n/2 до -1. С этим были проблемы…

Полученное решение можно видеть на графике в виде «водопада» линий распределения температуры по х для каждого момента времени t. Видно, что решение испытывает ~~сильные осциляции~~ численную неустойчивость, связано это с невыполнением критерия Куранта. Избавиться от неустойчивости можно уменьшив шаг по времени, либо применяя более продвинутую неявную схему, например Кранка-Николсона.

Двумерное уравнение диффузии

Начальные условия: u0 = 1 + sin(2X) + cos(2Y), где u теперь 2d-массив u(i,j). Используем неявную схему интегрирования по времени (т.е. выразим m+1 шаг через m-й):

Можно доказать, что такая неявная схема никогда не расходится при η>0.5, будем использовать η=1. Таким образом каждое новое значение u m+1 получаем умножением u m на коэффициент μ_k, зависящий от временного шага и волновых чисел k, т.е. μ_k — это константа, которую не нужно пересчитывать на каждом шаге!

Двумерное волновое уравнение

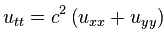
В волновом уравнении присутствует вторая производная по времени, поэтому задача сводится к системе двух обыкновенных диффуров, одна переменная — u, вторая — u_t, схему по времени в коде использовал самую простую явную, поэтому точность небольшая, шаг по времени очень маленький, зато код выглядит относительно просто. Впрочем, этого хватает для демонстрации работоспособности метода.

Периодичные граничные условия:

Фиксированные граничные условия (0 на краях, отражение волн от границ):

Выводы

В статье продемонстрировано несколько примеров применения спектрального метода для простых задач матфизики. Основная суть суть спектрального метода, это замена исходных диффренциальных уравнений в частных произодных на обыкновенные диффуры для коэффициентов разложения искомых функций по некоторому базису. Базисом могут быть синусы-косинусы, комплексные экспоненты, ортогональные полиномы, если требует геометрия — цилиндрические или сферические функции. Найденные коэффициенты в каждый момент времени позволяют восстановить искомое решение, а алгоритм FFT позволяет делать это быстро.

Преимуществами метода являются:

Видео:Урок 455. Уравнение ШрёдингераСкачать