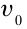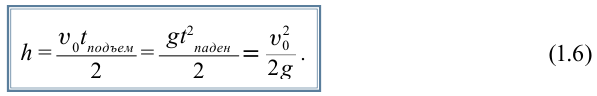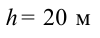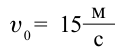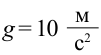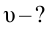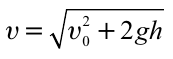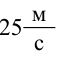Вертикальное движение тел:
Если держать в руках какой-либо предмет, а затем отпустить его, то предмет из-за притяжения Земли начнет двигаться прямо к ее поверхности. Такое движение тел называется вертикальное движение вниз. С этим движением вы ознакомились на уроках физики в 7 классе. В этой теме мы рассмотрим вертикальное движение вниз с точки зрения принципа независимости движений.
Когда тело двигается вертикально, на него действует одна или несколько сил (сила тяжести, сила сопротивления воздуха, сила Архимеда). В случае движения тел вверх (вертикально) в целях упрощения задачи мы не учитываем силу сопротивления воздуха и силу Архимеда.
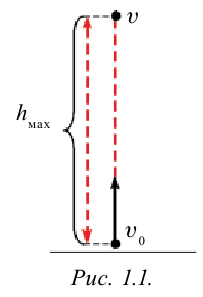
Понаблюдаем за движением какого-либо предмета, подбросив его вверх в вертикальном направлении (рис. 1.1.). Если бы тело двигалось вверх только со скоростью 
Движение тела, брошенного вертикально вверх, является равнозамедленным движением.
Скорость тела через время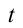 
определяется с помощью выражения:
Тело останавливается при достижении самой верхней точки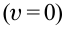 
и начинает вертикальное движение вниз.
Приравнивая левую сторону выражения (1.4) нулю, находим выражение для определения времени, необходимого для подъема тела:
Максимальная высота подъема тела определяется выражением:
В условиях, когда сопротивление воздуха ничтожно мало и можно его не учитывать, время подъема брошенного вверх тела будет равно времени падения вниз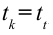 
, т.е. с какой скоростью тело будет брошено вертикально вверх, то с такой же скоростью тело вернется вниз.
Тело, брошенное вертикально вниз, совершает равномерно ускоренное движение. Здесь скорость тела через время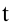 
определяется выражением:
Уравнение движения тела, брошенного вертикально вниз, запишем следующим образом:
Первым закономерности вертикального движения тел экспериментальным способом начал изучать великий итальянский ученый Г. Галилей. На основе проведенных опытов были обнаружены две закономерности вертикального падения тел. Во-первых, вертикальное падение тела является прямолинейным равноускоренным движением, во-вторых, все тела при свободном падении двигаются с постоянным ускорением.
Если учесть, что свободное падение тел является равноускоренным движением, то все уравнения прямолинейного равноускоренного движения в этом случае также действительны, т.е. можно заменить ускорение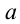 
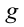
на ускорение свободного падения 
, путь 
на высоту 
(табл. 1).
Из-за того, что свободное падение происходит равноускоренно, а движение вертикально вверх – равнозамедленно, среднюю скорость движения тела можно определить из следующего выражения:
Образец решения задачи:
Начальная скорость предмета, падающего с крыши здания высотой
20 м, равна 15 м/сек. Чему равняется его скорость в момент столкновения
с землей?
Решение: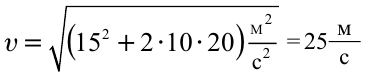 
Ответ: 
| Уравнения равноускоренного движения | Уравнения движения при свободном падении |
|---|---|
 |  |
 |  |
 |  |
 |  |
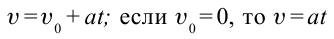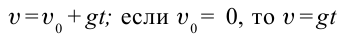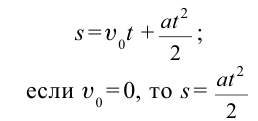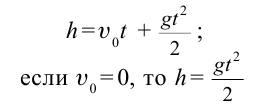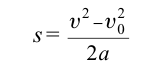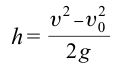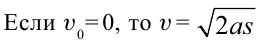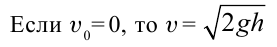| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Неравномерное движение по окружности
- Равномерное движение по окружности
- Взаимная передача вращательного и поступательного движения
- Движение горизонтально брошенного тела
- Опыты Фарадея в физике
- Электромагниты и их применение в физике
- Колебательный контур в физике
- Исследовательские методы в физике
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
- Движение тела, брошенного вертикально вверх (вниз)
- Механическое движение
- Механическое движение
- Прямолинейное равномерное движение
- Скалярные величины (определяются только значением)
- Векторные величины (определяются значением и направлением)
- Проецирование векторов
- Уравнение движения
- Прямолинейное равноускоренное движение
- Уравнение движения и формула конечной скорости
- Движение по вертикали
- 📽️ Видео
Видео:Теория движение тела брошенного вертикально вверхСкачать
Движение тела, брошенного вертикально вверх (вниз)
Начнем с утверждения, что
все тела на Земле, брошенные вертикально вверх, брошенные вертикально вниз и свободно падающие, — все они падают вниз или летят вверх с одним и тем же ускорением — ускорением свободного падения .
Надо сказать, что во всех трех случаях:
- бросание тела вверх
- бросание тела вниз
- свободное падение тела
— во всех этих трех случаях ускорение свободного падения направлено исключительно вниз. Вертикально вниз.
- В случае подбрасывания вверх движение тела — равнозамедленное (начальная скорость направлена вверх, ускорение — вниз — оно тормозит тело);
- В случае бросания вниз движение тела — равноускоренное;
- Также движение тела равноускоренное и в случае свободного падения с нулевой начальной скоростью.
Это утверждение бывает трудно воспринять. Жизнь нам показывает другое: камень и перышко падают по-разному. Камень падает быстро, а перышко спускается медленно. Никак нельзя сказать, что движение у них происходит с одним и тем же ускорением. Да, это так, но падение в этом случае — не свободное . Им мешает воздух. Есть такой классный опыт — трубка Галилея. В нем перышко и камень падают внутри трубки, из которой откачан воздух.
Движение там происходит действительно почти одинаково. Можете сами посмотреть видео .
Обратите внимание на то, что тела, подброшенные вертикально вверх, летят вверх с тем же ускорением свободного падения. Пока тело летит вверх, это ускорение направлено в сторону, противоположную движению. Оно замедляет движение вверх. Подброшенное вверх тело достигает верхней точки траектории и начинает падать вниз с тем же ускорением. Движение тела, брошенного вертикально вверх, — равноускоренное движение. При этом ускорение тела одинаково и направлено в сторону земли и тогда, когда тело летит вверх, и тогда, когда оно падает вниз.
Разбираться в этой теме лучше всего на конкретных задачах.
Шаг 1. Сделаем рисунок.
На рисунке обязательно надо указывать:
- вектор ускорения свободного падения
- ось для проектирования
- вектор начальной скорости.
Шаг 2. Мы знаем, что движение происходит под действием ускорения свободного падения. То есть движение равноускоренное. Для равноускоренного движения мы знаем следующие формулы, которые описывают зависимость координаты от времени и проекции скорости от времени:
«Адаптируем» эти уравнения к нашему случаю. Что это значит? Запишем правильные значения начальной координаты x 0 x_0 x 0 , начальной скорости V 0 x V_ V 0 x и ускорения a x a_x a x .
Тогда наши формулы перепишутся в виде:
Или, если подставить числа и упростить:
Мы записали уравнения изменения координаты и проекции скорости.
Шаг 3. Теперь построим графики зависимости координаты и проекции скорости от времени.
Чтобы найти точки пересечения параболы с осью абсцисс, решим уравнение 2 t − 5 t 2 = 0 2t-5t^2=0 2 t − 5 t 2 = 0 :
Все нужное мы записали и построили.
Шаг 4. Предлагаем немного проанализировать полученные решения. Посмотрим на графики. Видно, что с увеличением времени координата сначала увеличивается — это наше тело подлетает наверх. Затем в момент времени 0 , 2 0,2 0 , 2 с тело достигает своей вершины — вершины параболы. Затем тело падает вниз и с увеличением времени координата все уменьшается и уменьшается.
Скорость. В начальный момент времени тело имело некоторую скорость. С увеличением времени (мы видим по графику) скорость все уменьшается, уменьшается и уменьшается, но ее проекция остается положительной. Это наше тело движется вверх. В верхней точке траектории тело «замирает» — скорость становится равной нулю. Затем тело начинает двигаться вниз. Скорость теперь уже направлена вниз — противоположно направлению оси O X OX O X . Поэтому проекция скорости становится отрицательной.
Последнее, что нам необходимо узнать в этой теме, — это значения координаты и скорости в некоторых особых точках. Это:
- максимальная высота подъема
- время подъема
- время полета (до падения)
- скорость в нижней точке траектории.
Удобнее всего рассмотреть конкретный пример.
б) максимальную высоту (относительно земли) h в е р ш и н ы h_ h в е р ш и н ы , на которую поднимается мячик;
в) скорость в момент пролета мячиком балкона при падении V б а л к о н V_ V б а л к о н ;
г) скорость в момент времени, когда мячик достигнет земли V з е м л я V_ V з е м л я .
Шаг 1. Прежде всего — сделаем рисунок, введем вертикальную ось.
Шаг 2. Запишем уравнения движения для нашего случая.
«Адаптируем» эти уравнения в общем виде к нашему конкретному случаю:
Подставим и числа тоже:
А теперь — самое главное (!).
Чтобы найти что-то в определенных точках траектории, нужно понять — чем эти точки отличаются от всех остальных точек траектории.
Найдем высоту подъема. Для этого подставим t в е р ш и н ы t_ t в е р ш и н ы в уравнение для координаты:
Мы справились с пунктами а) и б).
Точка пролета балкона и точка падения уникальны тем, что в них известны координаты. В точке пролета балкона y б а л к о н а = h = 1 y_=h=1 y б а л к о н а = h = 1 , а в нижней точке координата равна нулю: y з е м л я = 0 y_=0 y з е м л я = 0 .
Проекция скорости получилась отрицательной, поскольку мячик летел уже вниз. Обратите внимание: скорость точно такая же, как была при броске. Просто направлена уже в другую сторону. Так проявляет себя закон сохранения механической энергии, к которому мы обратимся немного позже.
Осталось найти скорость в момент времени, когда мячик достигнет земли. В нижней точке y з е м л я = 0 y_=0 y з е м л я = 0 . Используем этот факт и найдем время, за которое мячик достигнет земли:
У этого квадратного уравнения два корня: t 1 = − 0 , 2 t_1=-0,2 t 1 = − 0 , 2 и t 2 = 1 t_2=1 t 2 = 1 .
Первый момент времени нас не устраивает, поскольку он отрицательный. А второй — устраивает. Именно этот момент времени соответствует падению мячика на землю.
Найдем скорость в этот момент времени. Для этого подставим время t = 1 t=1 t = 1 в уравнение скорости V y = 4 − 1 0 t V_y=4-10t V y = 4 − 1 0 t :
Скорость получилась отрицательная, поскольку мячик летит вниз, а ось направлена вверх.
Еще раз резюме : чтобы найти какие-то величины в особых точках, нужно использовать их «особенности»; на вершине траектории скорость равна нулю, а в определенных точках траектории обычно известна координата тела.
Задачи для самостоятельного решения: #движение по вертикали
Видео:9 класс, 10 урок, Движение тела, брошенного вертикально вверхСкачать
Механическое движение
О чем эта статья:
Видео:Уравнение движенияСкачать
Механическое движение
Когда мы идем в школу или на работу, автобус подъезжает к остановке или сладкий корги гуляет с хозяином, мы имеем дело с механическим движением.
Механическим движением называется изменение положения тел в пространстве относительно других тел с течением времени.
«Относительно других тел» — очень важные слова в этом определении. Для описания движения нам нужны:
- тело отсчета
- система координат
- часы
В совокупности эти три параметра образуют систему отсчета.
В механике есть такой раздел — кинематика. Он отвечает на вопрос, как движется тело. Дальше мы с помощью кинематики опишем разные виды механического движения. Не переключайтесь 😉
Прямолинейное равномерное движение
Движение по прямой, при котором тело проходит равные участки пути за равные промежутки времени называют прямолинейным равномерным. Это любое движение с постоянной скоростью.
Например, если у вас ограничение скорости на дороге 60 км/ч, и у вас нет никаких препятствий на пути — скорее всего, вы будете двигаться прямолинейно равномерно.
Мы можем охарактеризовать это движение следующими величинами.
Скалярные величины (определяются только значением)
- Время — в международной системе единиц СИ измеряется в секундах [с].
- Путь — длина траектории (линии, по которой движется тело). В случае прямолинейного равномерного движения — длина отрезка [м].
Векторные величины (определяются значением и направлением)
- Скорость — характеризует быстроту перемещения и направление движения материальной точки [м/с].
- Перемещение — вектор, проведенный из начальной точки пути в конечную [м].
Видео:Свободное падение тел. 10 класс.Скачать
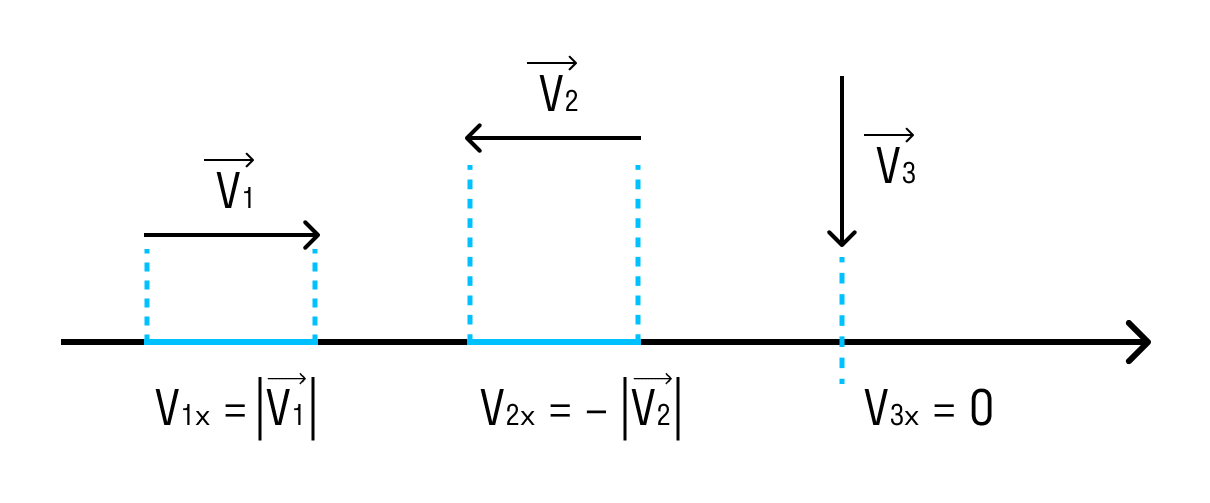
Проецирование векторов
Векторное описание движения полезно, так как на одном чертеже всегда можно изобразить много разнообразных векторов и получить перед глазами наглядную «картину» движения.
Однако всякий раз использовать линейку и транспортир, чтобы производить действия с векторами, очень трудоёмко. Поэтому эти действия сводят к действиям с положительными и отрицательными числами — проекциями векторов.
Если вектор сонаправлен с осью, то его проекция равна длине вектора. А если вектор противоположно направлен оси — проекция численно равна длине вектора, но отрицательна. Если вектор перпендикулярен — его проекция равна нулю.
Скорость может определяться по вектору перемещения и пути, только это будут две разные характеристики.
Скорость — это векторная физическая величина, которая характеризует быстроту перемещения, а средняя путевая скорость — это отношение длины пути ко времени, за которое путь был пройден.
Скорость
— скорость [м/с]
— перемещение [м]
— время [с]
Средняя путевая скорость
V ср.путевая = S/t
V ср.путевая — средняя путевая скорость [м/с]
S — путь [м]
t — время [с]
Задача
Найдите, с какой средней путевой скоростью должен двигаться автомобиль, если расстояние от Санкт-Петербурга до Великого Новгорода в 210 километров ему нужно пройти за 2,5 часа. Ответ дайте в км/ч.
Решение:
Возьмем формулу средней путевой скорости
V ср.путевая = S/t
Подставим значения:
V ср.путевая = 210/2,5 = 84 км/ч
Ответ: автомобиль будет двигаться со средней путевой скоростью равной 84 км/ч
Уроки физики в онлайн-школе Skysmart не менее увлекательны, чем наши статьи!
Видео:Урок 37. Движение тела, брошенного под углом к горизонту (начало)Скачать
Уравнение движения
Одной из основных задач механики является определение положения тела относительно других тел в данный момент времени. Для решения этой задачи помогает уравнение движения, то есть зависимость координаты тела от времени х = х(t).
Уравнение движения
x(t) — искомая координата в момент времени t [м]
x0 — начальная координата [м]
vx — скорость тела в данный момент времени [м/с]
t — момент времени [с]
Если положительное направление оси ОХ противоположно направлению движения тела, то проекция скорости тела на ось ОХ отрицательна, скорость меньше нуля (v
