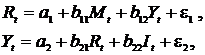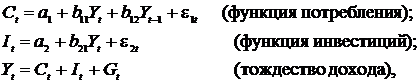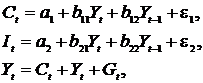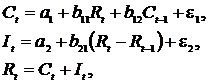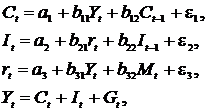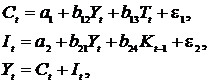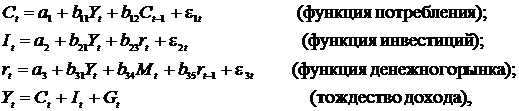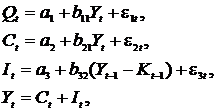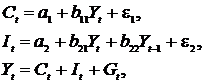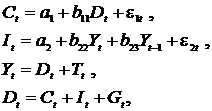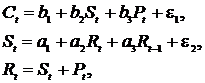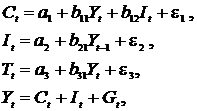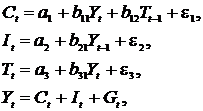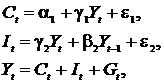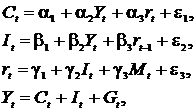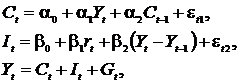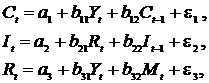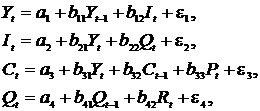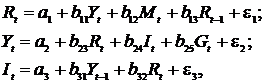Работа №2 Системы эконометрических уравнений
Пример решения типовой задачи
Изучается модель вида
где 
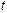














Первое уравнение – функция потребления, второе уравнение – функция инвестиций, третье уравнение – функция денежного рынка, четвертое уравнение – тождество дохода.
Модель представляет собой систему одновременных уравнений. Проверим каждое ее уравнение на идентификацию.
Модель включает четыре эндогенные переменные 


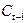

Проверим необходимое условие идентификации для каждого из уравнений модели.
Первое уравнение: 


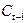



Второе уравнение: 




Третье уравнение: 

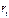


Четвертое уравнение: 
Проверим для каждого уравнения достаточное условие идентификации. Для этого составим матрицу коэффициентов при переменных модели.
 |  |  |  |  |  |  |  |
| I уравнение | –1 | 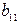 |  | ||||
| II уравнение | –1 | 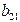 |  | ||||
| III уравнение | –1 |  |  | ||||
| Тождество | –1 |
В соответствии с достаточным условием идентификации ранг матрицы коэффициентов при переменных, не входящих в исследуемое уравнение, должен быть равен числу эндогенных переменных модели без одного.
Первое уравнение. Матрица коэффициентов при переменных, не входящих в уравнение, имеет вид
 |  |  |  |  |
| II уравнение | –1 | 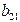 | 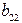 | |
| III уравнение | –1 |  | ||
| Тождество |
Ранг данной матрицы равен трем, так как определитель квадратной подматрицы 

Достаточное условие идентификации для данного уравнения выполняется.
Второе уравнение. Матрица коэффициентов при переменных, не входящих в уравнение, имеет вид
 | 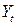 | 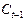 |  |  |
| I уравнение | –1 |  |  | |
| III уравнение |  |  | ||
| Тождество | –1 |
Ранг данной матрицы равен трем, так как определитель квадратной подматрицы 

Достаточное условие идентификации для данного уравнения выполняется.
Третье уравнение. Матрица коэффициентов при переменных, не входящих в уравнение, имеет вид
 |  |  | 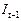 |  |
| I уравнение | –1 |  | ||
| II уравнение | –1 | 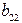 | ||
| Тождество |
Ранг данной матрицы равен трем, так как определитель квадратной подматрицы 

Достаточное условие идентификации для данного уравнения выполняется.
Таким образом, все уравнения модели сверхидентифицируемы. Приведенная форма модели в общем виде будет выглядеть следующим образом:
Задание на практическую работу
1 часть. Выполняется по индивидуальным вариантам
1. Даны системы эконометрических уравнений.
Требуется
1. Применив необходимое и достаточное условие идентификации, определите, идентифицируемо ли каждое из уравнений модели.
2. Определите метод оценки параметров модели.
3. Запишите в общем виде приведенную форму модели.
Вариант 1
Модель протекционизма Сальватора (упрощенная версия):







Вариант 2
Макроэкономическая модель (упрощенная версия модели Клейна):
 | где  – потребление; – потребление;  – инвестиции; – инвестиции; 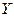 – доход; – доход;  – налоги; – налоги;  – запас капитала; – запас капитала;  – текущий период; – текущий период;  – предыдущий период. – предыдущий период. |
Вариант 3
Макроэкономическая модель экономики США (одна из версий):
 | где  – потребление; – потребление;  – ВВП; – ВВП;  – инвестиции; – инвестиции;  – процентная ставка; – процентная ставка;  – денежная масса; – денежная масса;  – государственные расходы; – государственные расходы;  – текущий период; – текущий период;  – предыдущий период. – предыдущий период. |
Вариант 4
Модель Кейнса (одна из версий):
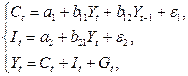 | где  – потребление; – потребление;  – ВВП; – ВВП;  – валовые инвестиции; – валовые инвестиции;  – государственные расходы; – государственные расходы;  – текущий период; – текущий период;  – предыдущий период. – предыдущий период. |
Вариант 5
Модель денежного и товарного рынков:
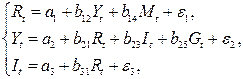 | где  – процентные ставки; – процентные ставки;  – реальный ВВП; – реальный ВВП;  – денежная масса; – денежная масса;  – внутренние инвестиции; – внутренние инвестиции; 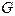 – реальные государственные расходы. – реальные государственные расходы. |
Вариант 6
Модифицированная модель Кейнса:
 | где  – потребление; – потребление;  – доход; – доход;  – инвестиции; – инвестиции;  – государственные расходы; – государственные расходы;  – текущий период; – текущий период;  – предыдущий период. – предыдущий период. |
Вариант 7
 | где  – расходы на потребление; – расходы на потребление; 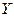 – чистый национальный продукт; – чистый национальный продукт;  – чистый национальный доход; – чистый национальный доход;  – инвестиции; – инвестиции;  – косвенные налоги; – косвенные налоги;  – государственные расходы; – государственные расходы;  – текущий период; – текущий период;  – предыдущий период. – предыдущий период. |
Вариант 8
Гипотетическая модель экономики:
 | где 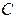 – совокупное потребление в период – совокупное потребление в период  ; ;  – совокупный доход в период – совокупный доход в период  ; ;  – инвестиции в период – инвестиции в период  ; ;  – налоги в период – налоги в период  ; ;  – государственные доходы в период – государственные доходы в период  . . |
Вариант 9
 | где Y — национальный доход; C — расходы на личное потребление; I — чистые инвестиции; Q — валовая прибыль экономики; P — индекс стоимости жизни; R — объем продукции промышленности. |
Вариант 10
где C – расходы на потребление, R — доход, I — инвестиции, t — текущий период, t-1 – предыдущий период.
Вариант 11
Конъюнктурная модель имеет вид:
где C – расходы на потребление, Y – ВВП, I – инвестиции, r – процентная ставка, M – денежная масса, G – государственные расходы, t – текущий период, t-1 – предыдущий период.
Вариант 12
Для прогнозирования спроса на свою продукцию предприятие использует следующую модель, характеризующую общую экономическую ситуацию в регионе:
где Q – реализованная продукция в период t, Y – ВДС региона, C – конечное потребление, I – инвестиции, K – запас капитала, t – текущий период, t-1 – предыдущий период.
Вариант 13
Дана следующая структурная форма модели:
где 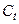




Вариант 14
Имеется модель кейнсианского типа:
где C – совокупное потребление в период t, Y – совокупный доход в период t, I – инвестиции в период времени t, T – налоги в период времени t, G – государственные расходы в период времени t, Yt-1 – совокупный доход в период t-1.
Вариант 15
Модель спроса и предложения на деньги:
где R – процентные ставки в период t, Y – ВВП в период t, M – денежная масса в период t, t – текущий период, t-1 – предыдущий период.
Вариант 16
Модель денежного рынка:
где R – процентные ставки, Y – ВВП, M – денежная масса, I – внутренние инвестиции, t – текущий период, t-1 – предыдущий период.
Вариант 17
Рассматривается следующая модель:
где 







Часть.
1. Дана модифицированная модель Кейнса:





| годы | |||||||||||||||||||
| Y | 95,75 | 98,55 | 103,55 | 108,25 | 107,4 | 112,7 | 117,75 | 123,45 | 126,55 | 125,85 | 128,1 | 125,35 | 130,25 | 138,3 | 142,65 | 146,80 | 151,3 | 157,4 | 161,25 |
| C | 60,45 | 62,45 | 65,9 | 68,9 | 68,45 | 73,55 | 76,55 | 79,7 | 81,6 | 81,55 | 82,55 | 83,45 | 87,35 | 91,55 | 95,50 | 101,75 | 105,4 | 107,45 | |
| I | 14,3 | 15,85 | 17,75 | 19,7 | 18,1 | 14,6 | 17,35 | 22,15 | 22,3 | 19,8 | 25,25 | 24,85 | 24,5 | 25,8 | 26,15 |
а) В предположении, что потребление зависит линейно от дохода (первое уравнение модели), оцените по МНК параметры 

б) Оцените те же параметры по ДМНК
в) Сравните полученные результаты. Сделайте выводы по качеству оценок.
Видео:Мультипликатор Кейнса - просто о сложномСкачать

Лабораторная работа № 3
Задание.
По заданным исходным данным для заданной модели (в соответствии с вариантом):
1. выделить эндогенные и экзогенные переменные;
2. применив необходимое и достаточное условие идентификации, определить, идентифицировано ли каждое из уравнений модели;
3. определить метод оценки параметров модели;
4. записать приведенную форму модели;
5. определить коэффициенты приведенной формы модели;
6. определить коэффициенты структурной формы модели;
Указания к решению. Для нахождения приведенных уравнений (а также коэффициентов структурных уравнений при применении ДМНК) рекомендуется использовать табличный процессор Excel (надстройка «Анализ данных», функция – расчет уравнения регрессии):
1) вызов модуля для нахождения регрессии – пункты меню: Сервис – Анализ данных – Регрессия.
2) указать ячейки, содержащие исходные значения y и x.
3) если отсутствует свободный член в уравнении регрессии – установить флажок «Константа–ноль».
Искомые значения коэффициентов линейного уравнения регрессии (a, bi)
берутся из столбца «Коэффициенты» таблицы результатов регрессии.
Требования к оформлению результатов
Отчет о лабораторной работе должен содержать разделы:
1. Описание задания;
2. Описание решения лабораторной работы (по этапам);
3. Изложение полученных результатов.
Варианты заданий к лабораторной работе № 3
Если иное не оговорено, то исходные данные берутся из Приложения 4.
4.1Модель спроса и предложения на деньги:
где Rt – процентные ставки в период t;
It – инвестиции в период t;
Mt – денежная масса в период t.
4.2Модель Кейнса (одна из версий):
где C – расходы на потребление;
I – валовые инвестиции;
G – государственные расходы;
t – текущий период; t-1 – предыдущий период.
4.3Одна из версий модифицированной модели Кейнса имеет вид
где C – расходы на потребление;
G – государственные расходы;
t – текущий период; t-1 – предыдущий период.
4.4Модель мультипликатора-акселератора:
где C – расходы на потребление;
t – текущий период; t-1 – предыдущий период.
4.5Конъюнктурная модель имеет вид:
где C – расходы на потребление;
r – процентная ставка;
M – денежная масса;
G – государственные расходы;
t – текущий период; t-1 – предыдущий период.
4.6Макроэкономическая модель (упрощенная модель Клейна):
где C – расходы на потребление;
K – запас капитала;
t – текущий период; t-1 – предыдущий период.
4.7Макроэкономическая модель экономики США (одна из версий):
где C – расходы на потребление;
r – процентная ставка;
M – денежная масса;
G – государственные расходы;
t – текущий период; t-1 – предыдущий период.
4.8Для прогнозирования спроса на свою продукцию предприятие использует следующую модель, характеризующую общую экономическую ситуацию в регионе:
где Q – реализованная продукция в период t;
C – конечное потребление;
K – запас капитала;
t – текущий период; t-1 – предыдущий период.
4.9Модифицированная модель Кейнса:
где C – расходы на потребление;
G – государственные расходы;
t – текущий период; t-1 – предыдущий период.
4.10Макроэкономическая модель:
где C – расходы на потребление;
Y – чистый национальный продукт;
D –чистый национальный доход;
T – косвенные налоги;
G – государственные расходы;
t – текущий период; t-1 – предыдущий период.
4.11Дана следующая структурная форма модели:
где Ct – расходы на потребление в период t;
St – зарплата в период t;
Pt – прибыль в период t;
Rt – общий доход в период t;
4.12Гипотетическая модель экономики:
где Ct – совокупное потребление в период t;
Yt – совокупный доход в период t;
It – инвестиции в период t;
Gt – государственные доходы в период t;
4.13Имеется следующая модель кейнсианского типа:
где C – совокупное потребление;
Y – совокупный доход;
G – государственные расходы;
t – текущий период; t-1 – предыдущий период.
4.14Имеется следующая макроэкономическая модель:
где Сt – расходы на потребление;
Gt – государственные расходы;
Yt – валовой национальный продукт в период t.
4.15Имеется следующая макроэкономическая модель:
где Ct – расходы на потребление;
Gt – государственные расходы.
4.16Имеется следующая макроэкономическая модель:
где C – расходы на потребление;
r – процентная ставка;
G – государственные расходы.
4.17Имеется следующая модель:
где Ct – расходы на потребление в период t;
Yt – совокупный доход период t:
It – инвестиции в период t;
Rt – процентная ставка в период t;
Mt – денежная масса в период t;
Ct-1 – расходы на потребление в период t-1;
4.18Модель Менгеса:
где Y – национальный доход;
C – расходы на потребление;
I – чистые инвестиции;
Q – валовая прибыль экономики;
P – индекс стоимости жизни;
R – объем продукции промышленности;
t – текущий период; t-1 – предыдущий период.
4.19Модель денежного и товарного рынков:
где R – процентные ставки;
Y – реальный ВВП;
M – денежная масса;
I – внутренние инвестиции;
G – реальные государственные расходы;
t – текущий период; t-1 – предыдущий период.
4.20Рассматривается модель:
Видео:Что такое мультипликаторы и как ими пользоваться: EBITDA, P/E, P/S, P/BV, ROE, EPSСкачать

Контрольная работа по эконометрике (стр. 4 )
 | Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 |

Темп роста валового
Для семи предприятий области анализируется зарплата 

Кол-во сотрудн., чел
Зарплата, тыс. тыс. руб.
По семи регионам приводятся следующие данные:
Среднедушевой прожиточный минимум в день одного трудоспособного, у. е. x
По семи регионам приводятся следующие данные:
Среднедушевой прожиточный минимум в день одного трудоспособного, у. е. x
Среднедневная заработная плата, у. е., y
По семи регионам приводятся следующие данные:
Среднедушевой прожиточный минимум в день одного трудоспособного, у. е. x
Среднедневная заработная плата, у. е., y
Пример 1. В эконометрических моделях часто наряду с уравнениями, параметры которых должны быть статистически оценены, используются балансовые тождества переменных, коэффициенты при которых равны 
Рассмотрим эконометрическую модель экономики страны:
где y1 – расходы на конечное потребление данного года; y2 – валовые инвестиции в текущем году; y3 – расходы на заработную плату в текущем году; y4 – валовой доход за текущий год; x1 — валовой доход предыдущего года; x2 – государственные расходы текущего года; а — свободный член уравнения, 
Решение. В этой модели четыре эндогенные переменные (y1, y2, y3, y4). Переменная y4 задана тождеством. Поэтому практически статистическое решение необходимо только для первых трех уравнений системы, которые необходимо проверить на идентификацию. Модель содержит две предопределенных переменных — экзогенную x2 и лаговую x1.
При практическом решении задачи на основе статистической информации за ряд лет или по совокупности регионов за один год в уравнениях для эндогенных переменных y1, y2, y3 обычно содержится свободный член (a1, a2, a3), значение которого аккумулирует влияние неучтенных в уравнении факторов и не влияет на определение идентифицируемости модели.
Поскольку фактические данные об эндогенных переменных y1, y2, y3 могут отличаться от теоретических постулируемых моделью, то принято в модель включать случайную составляющую для каждого уравнения системы, исключив тождества. Случайные составляющие обозначены через 
П е р в о е у р а в н е н и е.
Н: эндогенных переменных три (


Выполняется необходимое равенство: M — m1 = 2 — 0 = 2 = k1 — 1 = 3 — 1 =2, следовательно, уравнение идентифицируемо.
Д: в первом уравнении отсутствуют y2, x1, x2. Построим матрицу из коэффициентов при них в других уравнениях системы:
Уравнение Отсутствующие переменные
Второе -1 
Третье 0 
Четвертое 1 0 1
Определитель матрицы не равен нулю, ранг матрицы равен 3; следовательно выполняется достаточное условие идентификации (r(A) = 3 = K — 1 = 4 — 1 = 3), и первое уравнение идентифицируемо.
В т о р о е у р а в н е н и е.
Н: эндогенных переменных две (y2, y3) — k2 = 2; предопределенных переменных одна (x1) — m2 = 1.
Выполняется необходимое равенство: M — m2 = 2 — 1 = 1 = k2 — 1 = 2 — 1 = 1, следовательно, уравнение идентифицируемо.
Д: во втором уравнении отсутствуют y1, y4 x2. Построим матрицу коэффициентов при них в других уравнениях системы:
Уравнение Отсутствующие переменные
Первое -1 
Третье 0 
Четвертое 1 -1 1
Определитель матрицы не равен нулю, ранг матрицы равен 3, следовательно, выполняется достаточное условие идентификации (r(A) = 3 = K — 1 = 4 — 1 = 3), и второе уравнение идентифицируемо.
Т р е т ь е у р а в н е н и е.
Н: эндогенных переменных две (y3, y4) — k3 =2; предопределенных переменных одна (x1) — m3 = 1.
Выполняется необходимое равенство: M — m3 = 2 — 1 = 1 = k3 — 1 = 1, следовательно, уравнение идентифицируемо.
Д: в третьем уравнении отсутствуют y1, y2, x2. Построим матрицу из коэффициентов при них в других уравнениях системы:
Уравнение Отсутствующие переменные
ПервоеВторое 0 -1 0 Четвертое 1 1 1
Определитель матрицы не равен нулю, ранг матрицы равен 3, следовательно, выполняется достаточное условие идентификации (r(A) = 3 = K — 1 = 4 — 1 = 3), и третье уравнение идентифицируемо.
Следовательно, исследуемая система идентифицируема.
Приведенная форма модели:
где C—расходы на потребление, Y –совокупный доход в период t, r – процентная ставка в период t, I – инвестиции в период t, M – денежная масса в период t, G – государственные расходы в период t, It-1 — инвестиции в период t-1, Ct-1 — расходы на потребление в период t, t – текущий период, t-1 – предыдущий период.
Модель включает четыре эндогенные переменные (


Проверим необходимое условие идентификации для уравнений модели.
Это уравнение включает две эндогенные переменные (

Уравнение II включает две эндогенные переменные (
Уравнение III включает две эндогенные переменные 
Четвертое уравнение представляет собой тождество, параметры которого известны. Поэтому идентифицировать это уравнение не нужно.
Проверим для каждого из уравнений достаточное условие идентификации. Для этого составим матрицу коэффициентов при переменных модели:
🎥 Видео
Эффект мультипликатораСкачать

Прикладные задачи анализа данных, лекция 1 — Генеративно-состязательные сетиСкачать
Фундаментальный анализ акций. Мультипликаторы. Коэффициенты. P/E, P/S, EPS, P/B, ROE, PEG.Скачать

Определение расстояния по угловой величинеСкачать

Мультипликатор Мультипликатора. Окончание продолжения.Скачать

Мультипликаторы платежеспособности и финансовой устойчивости | Global FinanceСкачать

Коэффициент p/b или p/bv. Как считать и применять данный мультипликатор? Инвестиции для начинающих.Скачать

Мультипликатор сбалансированного бюджета Воздействие трансфертных платежейСкачать

Что такое P/E | Фундаментальный анализ | МультипликаторыСкачать

6.1 Численные методы решения задачи Коши для ОДУСкачать
Консультация по Анализу данных начального уровня-2024_2Скачать
Проверка оператора на линейностьСкачать

Проверка адекватности моделиСкачать

Линейная регрессияСкачать

Смысл и назначение мультов)))Скачать

Урок 4.2 - Рыночные мультипликаторы EV, РS и EBITDAСкачать

Симметричный мультивибратор. Принцип работы. Практические расчёты и эксперименты.Скачать

Модели атрибуции I Яндекс про Директ 2.0Скачать