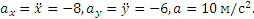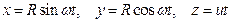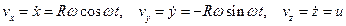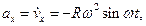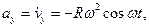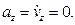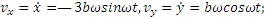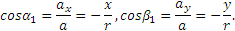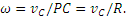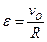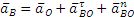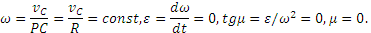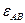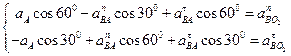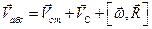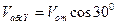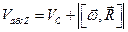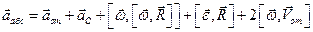В очередной раз меня попросили решить пару задачек по физике, и я вдруг обнаружил, что не могу решить их с ходу. Немного погуглив, я обнаружил, что сайты в топе выдачи содержат сканы одного и того же учебника и не описывают конкретных примеров решений задачи о том, как найти вектор скорости и ускорения материальной точки. По-этому я решил поделиться с миром примером своего решения.
- Траектория движения материальной точки через радиус-вектор
- Вектор скорости материальной точки
- Пример нахождения вектора скорости
- Как найти вектор ускорения материальной точки
- Модуль вектора скорости точки
- Модуль вектора ускорения
- Еще примеры решений задачи нахождения вектора скорости и ускорения
- Примеры решения задач. Движение точки задано уравнениями (х, у — в метрах, t — в секундах).
- Движение материальной точки задано уравнениями определить модули скорости и ускорения
- 🌟 Видео
Видео:Траектория и уравнения движения точки. Задача 1Скачать

Траектория движения материальной точки через радиус-вектор
Подзабыв этот раздел математики, в моей памяти уравнения движения материальной точки всегда представлялись при помощи знакомой всем нам зависимости y(x) , и взглянув на текст задачи, я немного опешил когда увидел векторы. Оказалось, что существует представление траектории материальной точки при помощи радиус-вектора – вектора, задающего положение точки в пространстве относительно некоторой заранее фиксированной точки, называемой началом координат.
Формула траектория движения материальной точки помимо радиус-вектора описывается так же ортами – единичными векторами i, j , k в нашем случае совпадающими с осями системы координат. И, наконец, рассмотрим пример уравнения траектории материальной точки (в двумерном пространстве):
Что интересного в данном примере? Траектория движения точки задается синусами и косинусами, как вы думаете, как будет выглядеть график в всем нам знакомом представлении y(x) ? “Наверное какой-то жуткий”, подумали вы, но все не так сложно как кажется! Попробуем построить траекторию движения материальной точки y(x), если она движется по представленному выше закону:
Здесь я заметил квадрат косинуса, если вы в каком-нибудь примере видите квадрат синуса или косинуса, это значит что нужно применять основное тригонометрическое тождество, что я и сделал (вторая формула) и преобразовал формулу координаты y, чтобы вместо синуса подставить в нее формулу изменения x:
В итоге жуткий закон движения точки оказался обычной параболой, ветви которой направлены вниз. Надеюсь, вы поняли примерный алгоритм построения зависимости y(x) из представления движения через радиус-вектор. Теперь перейдем к нашему главному вопросу: как же найти вектор скорости и ускорения материальной точки, а так же их модули.
Видео:К1 Определение скорости и ускорения точки по заданным уравнениям ее движенияСкачать

Вектор скорости материальной точки
Всем известно, что скорость материальной точки – это величина пройденного пути точкой за единицу времени, то есть производная от формулы закона движения. Чтобы найти вектор скорости нужно взять производную по времени. Давайте рассмотрим конкретный пример нахождения вектора скорости.
Пример нахождения вектора скорости
Имеем закон перемещения материальной точки:
Теперь нужно взять производную от этого многочлена, если вы забыли как это делается, то вот вам таблица производных различных функций. В итоге вектор скорости будет иметь следующий вид:
Все оказалось проще, чем вы думали, теперь найдем вектор ускорения материальной точки по тому же самому закону, представленному выше.
Видео:Лекция №1 "Кинематика материальной точки" (Булыгин В.С.)Скачать

Как найти вектор ускорения материальной точки
Вектор ускорения точки это векторная величина, характеризующая изменение с течением времени модуля и направления скорости точки. Чтобы найти вектор ускорения материальной точки в нашем примере, нужно взять производную, но уже от формулы вектора скорости, представленной чуть выше:
Видео:Скорости и ускорения точек вращающегося телаСкачать

Модуль вектора скорости точки
Теперь найдем модуль вектора скорости материальной точки. Как вы знаете из 9-го класса, модуль вектора – это его длина, в прямоугольных декартовых координатах равна квадратному корню из суммы квадратов его координат. И откуда же из полученного нами выше вектора скорости взять его координаты спросите вы? Все очень просто:
Теперь достаточно только подставить время, указанное в задаче и получить конкретное числовое значение.
Видео:УСКОРЕНИЕ - Что такое равноускоренное движение? Как найти ускорение // Урок Физики 9 классСкачать

Модуль вектора ускорения
Как вы поняли из написанного выше (и из 9-го класса), нахождение модуля вектора ускорения происходит тем же образом, что и модуля вектора скорости: извлекаем корень квадратный из суммы квадратов координат вектора, все просто! Ну и вот вам, конечно же, пример:
Как вы видите, ускорение материальной точки по заданному выше закону не зависит от времени и имеет постоянную величину и направление.
Видео:Урок 7. Механическое движение. Основные определения кинематики.Скачать

Еще примеры решений задачи нахождения вектора скорости и ускорения
А вот тут вы можете найти примеры решения и других задач по физике на тему “механика твердых тел”. А для тех, кто не совсем понял как найти вектор скорости и ускорения, вот вам еще парочка примеров из сети без всяких лишних объяснений, надеюсь, они вам помогут.
Если у вас возникли какие-нибудь вопросы, вы можете задать их в комментариях.
Видео:Физика - перемещение, скорость и ускорение. Графики движения.Скачать

Примеры решения задач. Движение точки задано уравнениями (х, у — в метрах, t — в секундах).
Задача 2.1.
Движение точки задано уравнениями (х, у — в метрах, t — в секундах).
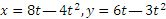
Определить траекторию, скорость и ускорение точки.
Решение.
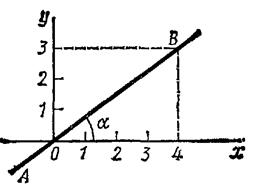 |
| Рис. 2.9. К задаче 2.1 |
Для определения траектории исключаем из уравнений движения время t. Умножая обе части первого уравнения на 3, а обе части второго — на 4 и почленно вычитая из первого равенства второе, получим: 
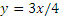
Следовательно, траектория — прямая линия, наклоненная к оси Ох под углом α, где 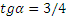
Определяем скорость точки. По формулам (2.1) получаем:
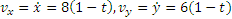
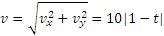
Теперь находим ускорение точки. Формулы (2.1) дают:
Направлены векторы 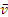
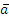
Заметим, наконец, что при 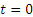
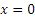
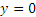
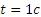
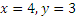
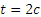
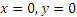
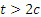
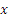
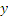
Итак, заданные в условиях задачи уравнения движения рассказывают нам всю историю движения точки. Движение начинается из точки О с начальной скоростью 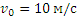
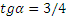
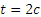
Задача 2.2.
Движение точки задано уравнениями:
где 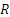
Решение.
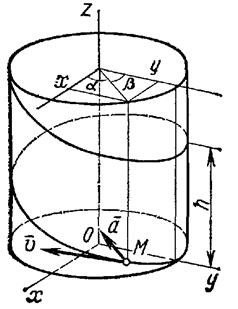 |
| Рис. 2.10. К задаче 2.2 |
Возводя первые два уравнения почленно в квадрат и складывая, получаем
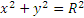
Следовательно, траектория лежит на круглом цилиндре радиуса R, ось которого направлена вдоль оси Oz (рис. 2.10). Определяя из последнего уравнения t и подставляя в первое, находим
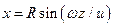
Таким образом, траекторией точки будет линия пересечения синусоидальной поверхности, образующие которой параллельны оси Оу (синусоидальный гофр) с цилиндрической поверхностью радиуса R. Эта кривая называется винтовой линией. Из уравнений движения видно, что один виток винтовой линий точка проходит за время 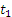
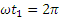
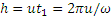
Найдем скорость и ускорение точки. Дифференцируя уравнения движения по времени, получаем:
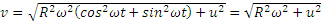
Стоящие под знаком радикала величины постоянны. Следовательно, движение происходит с постоянной по модулю скоростью, направленной по касательной к траектории. Теперь по формулам (2.1) вычисляем проекции ускорения;
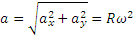
Итак, движение происходит с постоянным по модулю ускорением, Для определения направления ускорения имеем формулы:
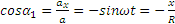
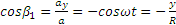
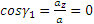
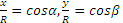
где α и β —углы, образуемые с осями Ох и Оу радиусом R, проведенным от оси цилиндра к движущейся точке. Так как косинусы углов α1 и β1 отличаются от косинусов α и β только знаками, то отсюда заключаем, что ускорение точки все время направлено по радиусу цилиндра к его оси.
Заметим, что хотя в данном случае движение и происходит со скоростью, постоянной по модулю, ускорение точки не равно нулю, так как направление скорости изменяется.
Задача 2.3.
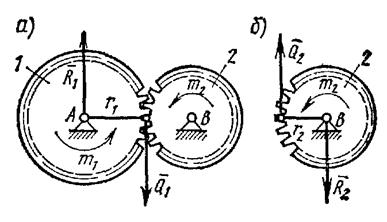
На шестерню 1 радиуса r1 действует пара сил с моментом m1 (рис. 46, а). Определить момент m2 пары, которую надо приложить к шестерне 2 радиуса r2, чтобы сохранить равновесие.
Решение.
 |
| Рис. 2.11. К задаче 2.3 |
Рассмотрим сначала условия равновесия шестерни 1. На нее действует пара с моментом m1, которая может быть уравновешена только действием другой пары, в данном случае пары 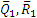
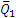
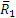
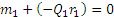
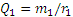
Теперь рассмотрим условия равновесия шестерни 2 (рис. 46, б). По закону равенства действия и противодействия на нее со стороны шестерни 1 будет действовать сила 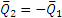
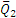
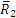
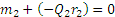
Естественно, что пары с моментами m1 и m2 не удовлетворяют условию равновесия , так как они приложены к разным телам.
Полученная в процессе решения задачи величина Q1 (или Q2) называется окружным усилием, действующим на шестерню. Как видим, окружное усилие равно моменту вращающей пары, деленному на радиус шестерни: Q1=m1/r1 =m2/r2.
Задача 2.4.
Человек ростом h удаляется от фонаря, висящего на высоте H, двигаясь прямолинейно со скоростью 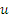
Решение.
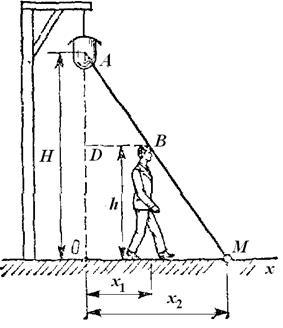 |
| Рис. 2.12. К задаче 2.4 |
Для решения задачи найдем сначала закон, по которому движется конец тени. Выбираем начало отсчета в точке О, находящейся на одной вертикали с фонарем, и направляем вдоль прямой, по которой движется конец тени, координатную ось Ох (рис. 2.12). Изображаем человека в произвольном положении на расстоянии x1 от точки О. Тогда конец его тени будет находиться от начала О на расстоянии х2.
Из подобия треугольников ОАМ и DAB находим:

Это уравнение выражает закон движения конца тени М, если закон движения человека, т.е. 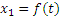
Взяв производную по времени от обеих частей равенства и замечая, что по формуле (2.1) 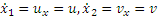
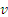
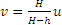
Если человек движется с постоянной скоростью ( 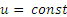
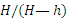
Обращаем внимание на то, что при составлении уравнений движения надо изображать движущееся тело или механизм в произвольном положении. Только тогда мы поучим уравнения, определяющие положение движущейся точки (или тела) в любой момент времени.
Задача 2.5.
Определить траекторию, скорость и ускорение середины М шатуна кривошипно-ползунного механизма (рис. 2.13), если OA=AB=2b, а угол 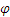
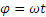
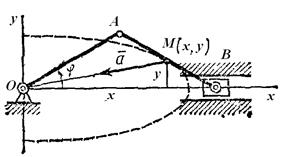 |
| Рис. 2.13. К задаче 2.5. |
Начинаем с определения уравнений движения точки М. Проводя оси и обозначая координаты точки М в произвольном положении через х и у находим
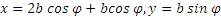
Заменяя 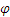
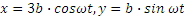
Для определения траектории точки М представим уравнения движения в виде
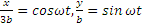
Возводя эти равенства почленно в квадрат и складывая, получим
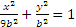
Итак, траектория точки М — эллипс с полуосями 3b и b.
Теперь по формуле (2.1) находим скорость точки М:
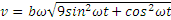
Скорость оказывается величиной переменной, меняющейся с течением времени в пределах от 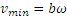
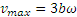
Далее по формулам (2.1) определяем проекции ускорения точки М;
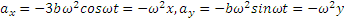
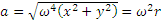
где 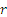
Определелим направление ускорения
Отсюда находим, что ускорение точки М все время направлено вдоль МО к центру эллипса.
Задача 2.6.
Вал, делающий n=90 об/мин, после выключения двигателя начинает вращаться равнозамедленно и останавливается через t1=40 с. Определить, сколько оборотов сделал вал за это время.
Решение.
Так как вал вращается равнозамедленно, то для него, считая 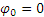
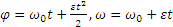
Начальной угловой скоростью при замедленном вращении является та, которую вал имел до выключения двигателя. Следовательно,
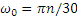
В момент остановки при t=t1 угловая скорость вала ω1=0. Подставляя эти значения во второе из уравнений (2.2), получаем:
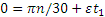
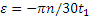
Если обозначить число сделанных валом за время t1 оборотов через N (не смешивать с n; n — угловая скорость), то угол поворота за то же время будет равен 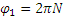
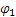
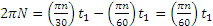
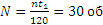
Задача 2.7.
Маховик радиусом R=0,6 м вращается равномерно, делая n=90 об/мин. Определить скорость и ускорение точки, лежащей на ободе маховика.
Решение.
Скорость точки обода 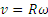
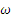
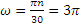
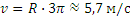
Далее, так как 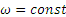
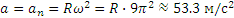
Ускорение точки направлено в данном случае к оси вращения.
Задача 2.8.
Найти скорость точки М обода колеса, катящегося по прямолинейному рельсу без скольжения (рис. 2.14), если скорость центра С колеса равна 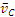
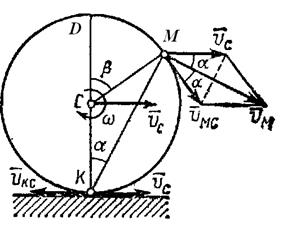 |
| Рис. 2.14. К задаче 2.8. |
Решение
Приняв точку С, скорость которой известна, за полюс, найдем, что 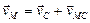
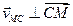
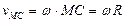
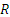
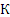
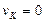
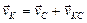
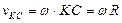
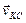
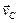
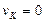
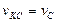
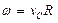
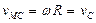
Параллелограмм, построенный на векторах 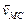
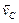
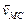
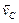
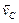
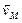
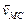
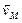
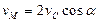
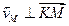
Задача 2.9.
Определить скорость точки М обода катящегося колеса, рассмотренного в предыдущей задаче, с помощью мгновенного центра скоростей.
Решение.
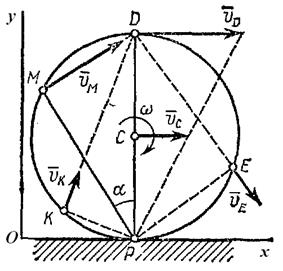 |
| Рис. 2.15. К задаче 2.9. |
Точка касания колеса Р (рис. 2.15) является мгновенным центром скоростей, поскольку 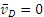
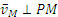
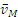
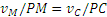
что 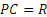
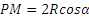
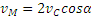
Чем точка М дальше от Р, тем ее скорость больше; наибольшую скорость 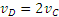
Аналогичная картина распределения скоростей имеет место при качении колеса или шестерни по любой цилиндрической поверхности.
Задача 2.10.
Центр О колеса, катящегося по прямолинейному рельсу (рис. 2.16), имеет в данный момент времени скорость 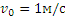
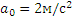
Решение.
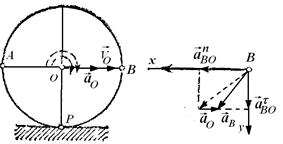 |
| Рис. 2.16. К задаче 2.10. |
1) Так как 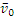
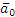
2) Определение ω. Точка касания Р является мгновенным центром скоростей; следовательно, угловая скорость колеса
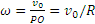
3) Определение ε. Так как величина PO=R остается постоянной при любом положении колеса, то
Знаки ω и ε совпадают, следовательно, вращение колеса ускоренное.
а) не следует думать, что если по условиям задачи 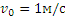
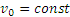
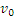
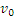
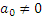
б) в данном случае 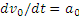
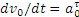
4) Определение 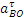
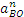
Учитывая, что в нашем случае BO=R, находим:
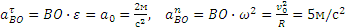
Показав на чертеже точку B отдельно, изображаем (без соблюдения масштаба) векторы, из которых слагается ускорение 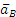
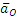
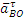
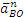
5) Вычисление 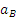
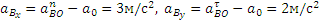
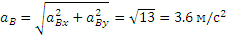
Аналогичным путем легко найти и ускорение точки P: 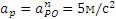
Задача 2.11.
Колесо катится по прямолинейному рельсу так, что скорость 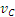
Решение.
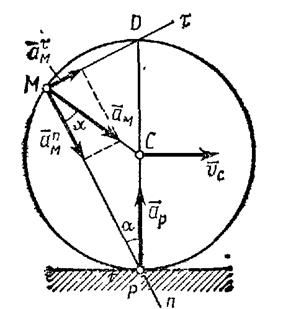 |
| Рис. 2.17. К задаче 2.11. |
Так как по условиям задачи 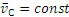
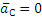
В результате ускорение точки М
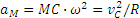
Таким образом, ускорение любой точки М обода (в том числе и точки Р) равно 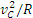
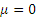
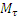
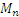
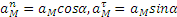
Зажача 2.12.
Плоский механизм состоит из стержней 1, 2, 3, 4 и ползуна С, соединенных друг с другом и с неподвижными опорами О1 и О2 шарнирами (рис.2.17 а). Точка D находится в середине стержня АВ. Длины стержней равны соответственно L1=0,4 м, L2 =1,2 м, L3=1,4 м, L4=0,6 м.
Дано: 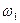
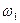
Найти: скорости точек В и C; угловую скорость 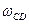
| а) | 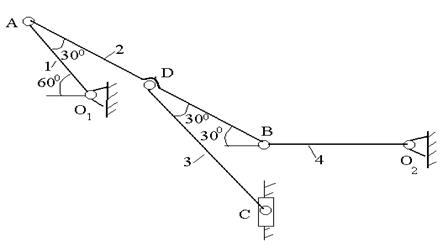 |
| б) | 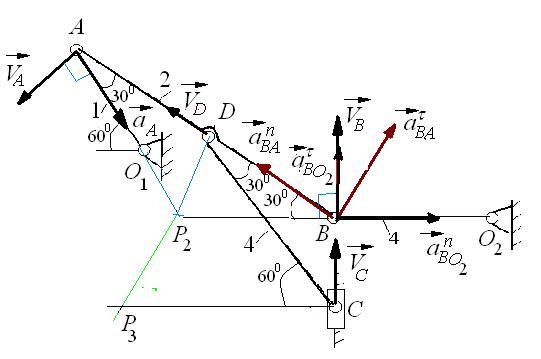 |
| Рис.2.17. К задаче 2.12. |
Решение (рис.2.12б)
1. Определим скорость точки А. Стержень OAвращается вокруг точко O1, поэтому скорость точки А определяется по формуле 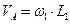
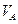
2. Определим угловую скорость стержня АВ. Точка В вращается вокруг центра О2, поэтому ее скорость перпендикулярна отрезку O2B. Для нахождения мгновенного центра скоростей отрезка АВ в точках А и В восстановим перпендикуляры к векторам 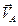
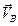
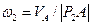
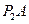
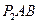
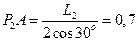
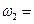
3. Определим скорость точки В по формуле 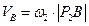
по формуле 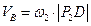
4. Определим скорость точки С. Так как точка С движется прямолинейно, то ее скорость направлена вдоль движения ползуна. Для нахождения мгновенного центра скоростей отрезка CD в точках C и D восстановим перпендикуляры к векторам 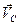
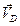
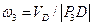
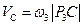
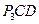
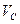
5. Определим угловую скорость отрезка О2В. Известно, что центром скоростей этого стержня является точка О2В , а также скорость точки B. Поэтому угловая скорость четвертого стержня вычисляется по формуле 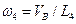
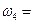
6. Определим ускорение точки А. Так как первый стержень вращается равномерно, то точка А имеет относительно О1 только нормальное ускорение, которое вычисляется по формуле 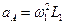
7. Определим ускорение точки В, которая принадлежит двум стержням — АВ и О2В. Поэтому ускорение точки В определяется с помощью двух формул
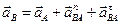
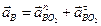
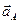
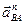
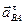
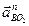
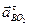
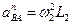
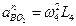
Можно составить уравнение
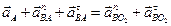
Решив полученную систему двух уравнений с двумя неизвестными, получим:
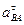
8. Определим угловое ускорение стержня АВ, используя формулу 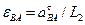
Задача 2.13.
Круглая пластина радиуса R=60 см вращается вокруг неподвижной оси по закону 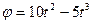
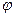
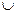
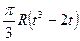
Найти абсолютную скорость и абсолютное ускорение точки М в момент времени t=1 с.
| а) | 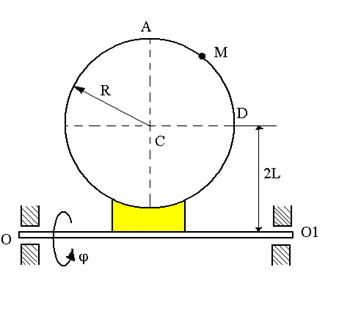 |
| б) | 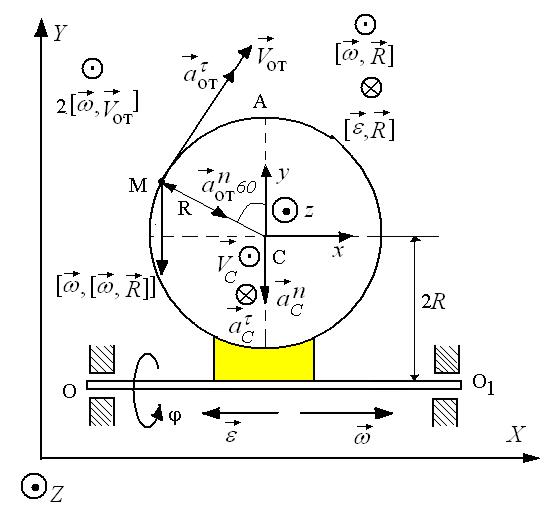 |
| Рис.2.18. К задаче 2.13. |
Решение (рис.2.13 б)
В качестве подвижной системы координат xyz примем точку С. Эта система совершает вращательное движение с угловой скоростью 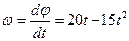
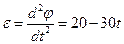
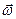
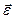
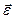
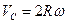
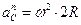
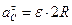
Вычислим путь, относительную скорость и ускорение точки M. Ее положение определяется величиной дуги S, в данный момент времени S = 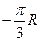
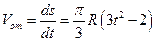
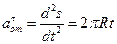
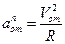
Абсолютная скорость точки M определяется по формуле
Где — 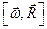
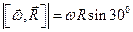
По теореме Пифагора 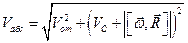
Абсолютное ускорение точки M определяется по формуле
Где 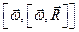
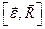
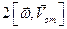
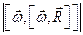
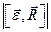
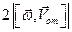
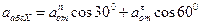
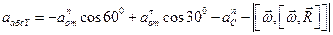
Видео:Кинематика точки Задание К1Скачать

Движение материальной точки задано уравнениями определить модули скорости и ускорения
Яблонский задание К.1. Определение скорости и ускорения точки по заданным уравнениям ее движения.
По заданным уравнениям движения точки M установить вид ее траектории и для момента времени t=t1 (с) найти положение точки на траектории, ее скорость, полное, касательное и нормальное ускорения, а также радиус кривизны траектории. Необходимые для решения данные приведены в таблице 20.
Дополнение к заданию К.1. Данное задание может быть использовано для определения скорости и ускорения точки при ее движении по пространственной траектории. Для этого к двум уравнениям движения (см. табл. 20) добавляется третье уравнение (табл. 22).
Общий порядок выполнения задания в этом случае такой же, как и в приведенном примере.
🌟 Видео
Кинематика точки. Три способа задания движения. Скорость, ускорениеСкачать

Физика 10 класс (Урок№3 - Равноускоренное движение материальной точки.)Скачать

14. Определение скорости и ускорения точки при векторном и координатном способах заданияСкачать

Физика 10 класс (Урок№2 - Равномерное прямолинейное движение материальной точки.)Скачать

Лекция 3.4 | Перемещение и скорость материальной точки | Александр Чирцов | ЛекториумСкачать

Кинематика материальной точки за 20 минут (кратко и доступно) Кинематика точкиСкачать

Консультация к устному экзамену. Механика. Часть 1: "Движение материальной точки"Скачать

Теоретическая механика. Задание К1 (часть 1) из сборника ЯблонскогоСкачать

Задача на движение материальной точки - bezbotvyСкачать

13.1. Определение сил по заданному движениюСкачать

ЕГЭ по математике. Профильный уровень. Задание 7. Закон движения. ПроизводнаяСкачать

Уравнение движения тела дано в виде x=2−3t. ВычислиСкачать