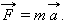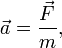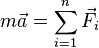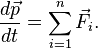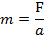К ранее рассмотренным кинематическим мерам изменения движения (скорости и ускорению) добавляются динамические меры изменения движения (количество движения и кинетический момент). Совместно с мерами действия сил они отражают взаимосвязь сил и движения. Изучение их помогает понять физические основы двигательных действий человека.
Динамика (от греч. dynamikós — сильный, от dýnamis — сила), раздел механики, посвященный изучению движения материальных тел под действием приложенных к ним сил. В основе динамики лежат три закона И. Ньютона, из которых как следствия получаются все уравнения и теоремы, необходимые для решения задач динамики. Все движения человека и движимых им тел под действием сил изменяются по величине и направлению скорости. Чтобы раскрыть механизм движений (причины их возникновения и ход их изменения), исследуют динамические характеристики. К ним относятся инерционные характеристики (особенности самих движущихся тел), силовые (особенности взаимодействия тел) и энергетические (состояния и изменения работоспособности, биомеханических систем).
Инерционные характеристики раскрывают особенности тела человека и движимых им тел в их взаимодействиях. От инерционных характеристик зависит сохранение и изменение скорости.
Все физические тела обладают свойством инертности (или инерции), которое проявляется в сохранении движения, а также в особенностях изменения его под действием сил.
Понятие инерции раскрывается в первом законе Ньютона: «Всякое тело сохраняет свое состояние покоя или равномерного и прямолинейного движения до тех пор, пока внешние приложенные силы не заставят его изменить это состояние».
Масса — это мера инертности тела при поступательном движении. Она измеряется отношением величины приложенной силы к вызываемому ею ускорению. Масса (m) — это количество вещества (в килограммах), содержащееся в теле или отдельном звене.
Масса тела характеризует, как именно приложенная сила может изменить движение тела. Одна и та же сила вызовет большее ускорение у тела с меньшей массой, чем у тела с большей массой.
Вес тела — это сила, с которой тело вследствие его притяжения к Земле действует на горизонтальную опору.
Момент инерции — это мера инертности тела при вращательном движении. Момент инерции тела относительно оси равен сумме произведений масс всех его частиц на квадраты их расстояний от данной оси вращения.
Отсюда видно, что момент инерции тела больше, когда его частицы дальше от оси вращения, а значит угловое ускорение тела под действием того же момента силы меньше; если частицы ближе к оси, то угловое ускорение больше, а момент инерции меньше. Значит, если приблизить тело к оси, то легче вызвать угловое ускорение, легче разогнать тело во вращении, легче и остановить его. Этим пользуются при движении вокруг оси.
Силовые характеристики. Известно, что движение тела может происходить как под действием приложенной к нему движущей силы, так и без движущей силы (по инерции), когда приложена только тормозящая сила. Движущие силы приложены не всегда; без тормозящих же сил движения не бывает. Изменение движений происходит под действием сил. Сила не причина движения, а причина изменения движения; силовые характеристики раскрывают связь действия силы с изменением движения.
Сила — это мера механического воздействия одного тела на другое в данный момент времени. Численно она определяется произведением массы тела и его ускорения, вызванного данной силой.
Чаще всего говорят про силу и результат ее действия, но это применимо только к простейшему поступательному движению тела. В движениях человека как системы тел, где все движения частей тела вращательные, изменение вращательного движения зависит не от силы, а от момента силы.
Момент силы — это мера вращающего действия силы на тело. Он определяется произведением силы на ее плечо.
Момент силы обычно считают положительным, когда сила вызывает поворот тела против часовой стрелки, и отрицательным при повороте по часовой стрелке.
Чтобы сила могла проявить свое вращающее действие, она должна иметь плечо. Иначе говоря, она не должна проходить через ось вращения.
Определение силы или момента силы, если известна масса или момент инерции, позволяет узнать только ускорение, т.е. как быстро изменяется скорость. Надо еще узнать, насколько именно изменится скорость. Для этого должно быть известно, как долго была приложена сила. Иначе говоря, следует определить импульс силы (или ее момента).
Импульс силы — это мера воздействия силы на тело за данный промежуток времени (в поступательном движении). Он равен произведению силы и продолжительности ее действия.
Любая сила, приложенная даже в малые доли секунды (например: удар по мячу), имеет импульс. Именно импульс силы определяет изменение скорости, силой же обусловлено только ускорение.
Во вращательном движении момент силы, действуя в течение определенного времени, создает импульс момента силы.
Импульс момента силы — это мера воздействия момента силы относительно данной оси за данный промежуток времени (во вращательном движении).
Вследствие импульса, как силы, так и момента силы возникают изменения движения, зависящие от инерционных свойств тела и проявляющиеся в изменении скорости (количество движения, кинетический момент).
Количество движения — это мера поступательного движения тела, характеризующая его способность передаваться другому телу в виде механического движения. Количество движения тела измеряется произведением массы тела на его скорость.
Кинетический момент (момент количества движения)— это мера вращательного движения тела, характеризующая его способность передаваться другому телу в виде механического движения. Кинетический момент равен произведению момента инерции относительно оси вращения на угловую скорость тела.
Соответствующее изменение количества движения происходит под действием импульса силы, а под действием импульса момента силы происходит определенное изменение кинетического момента (момента количества движения).
Энергетические характеристики. Энергия (от греч. enérgeia — действие, деятельность), общая количественная мера движения и взаимодействия всех видов материи. Энергия в природе не возникает из ничего и не исчезает; она только может переходить из одной формы в другую. Механическая энергия — энергия механического движения и взаимодействия тел системы или их частей. Механическая энергия равна сумме кинетической и потенциальной энергии механической системы.
При движениях человека силы, приложенные к его телу на некотором пути, совершают работу и изменяют положение и скорость звеньев тела, что изменяет его энергию. Работа характеризует процесс, при котором меняется энергия системы. Энергия же характеризует состояние системы, изменяющейся вследствие работы. Энергетические характеристики показывают, как меняются виды энергии при движении, и протекает сам процесс изменения энергии.
Работа силы — это мера действия силы на тело при некотором его перемещении под действием этой силы. Она равна произведению модуля силы и перемещения точки приложения силы.
Если сила направлена в сторону движения (или под острым углом к этому направлению), то она совершает положительную работу, увеличивая энергию движения тела. Когда же сила направлена навстречу движению (или под тупым углом к его направлению), то работа силы отрицательная и энергия движения тела уменьшается.
Работа момента силы — это мера воздействия момента силы на тело на данном пути (во вращательном движении). Она равна произведению модуля момента силы и угла поворота.
Понятие работы представляет собой меру внешних воздействий, приложенных к телу на определенном пути, вызывающих изменения механического состояния тела.
Энергия — это запас работоспособности системы. Механическая энергия определяется скоростями движений тел в системе и их взаимным расположением; значит, это энергия перемещения и взаимодействия.
Кинетическая энергия тела — это энергия его механического движения, определяющая возможность совершить работу. При поступательном движении она измеряется половиной произведения массы тела на квадрат его скорости, при вращательном движении половиной произведения момента инерции на квадрат его угловой скорости.
Потенциальная энергия тела — то энергия его положения, обусловленная взаимным относительным расположением тел или частей одного и того же тела и характером их взаимодействия. Потенциальная энергия в поле сил тяжести определяется произведением силы тяжести на разность уровней начального и конечного положения над землей (относительно которого определяется энергия).
Энергия как мера движения материи переходит из одного вида в другой. Так, химическая энергия в мышцах превращается в механическую (внутреннюю потенциальную упруго-деформированных мышц). Порожденная последней сила тяги мышц совершает работу и преобразует потенциальную энергию в кинетическую энергию движущихся звеньев тела и внешних тел. Механическая энергия внешних тел (кинетическая), передаваясь при их действии на тело человека его звеньям, преобразуется в потенциальную энергию растягиваемых мышц-антаганистов, а также в рассеивающуюся тепловую энергию.
Видео:Основное уравнение динамики вращательного движения. 10 класс.Скачать

Второй закон Ньютона. Динамические уравнения движения
Второй закон Ньютона – основной закон динамики. Этот закон выполняется только в инерциальных системах отсчета.
Приступая к формулировке второго закона, следует вспомнить, что в динамике вводятся две новые физические величины – масса тела m и сила 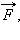
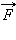
Второй закон Ньютона – это фундаментальный закон природы; он является обобщением опытных фактов, которые можно разделить на две категории:
- Если на тела разной массы подействовать одинаковой силой, то ускорения, приобретаемые телами, оказываются обратно пропорциональны массам:
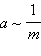 при F = const. при F = const. |
- Если силами разной величины подействовать на одно и то же тело, то ускорения тела оказываются прямо пропорциональными приложенн силам:
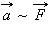 при m = const. при m = const. |
Обобщая подобные наблюдения, Ньютон сформулировал основной закон динамики:
Сила, действующая на тело, равна произведению массы тела на сообщаемое этой силой ускорение:
|
Это и есть второй закон Ньютона. Он позволяет вычислить ускорение тела, если известна его масса m и действующая на тело сила 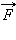
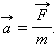 |
В Международной системе единиц (СИ) за единицу силы принимается сила, которая сообщает телу массой 1 кг ускорение 1 м/с 2 . Эта единица называется ньютоном (Н). Ее принимают в СИ за эталон силы (см. §1.7):
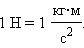 |
Если на тело одновременно действуют несколько сил (например, 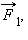
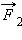
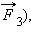
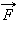
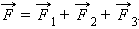 |
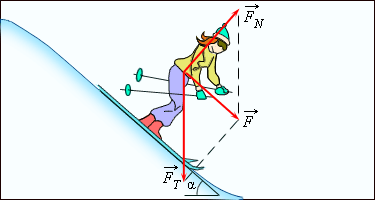 |
Рисунок 1.8.1. Сила 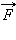 – равнодействующая силы тяжести – равнодействующая силы тяжести 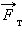 и силы нормального давления и силы нормального давления 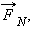 действующих на лыжницу на гладкой горе. Сила действующих на лыжницу на гладкой горе. Сила 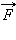 вызывает ускорение лыжника вызывает ускорение лыжника |
Если равнодействующая сила 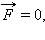
Второй закон Ньютона[править | править вики-текст]
Основная статья: Второй закон Ньютона
Второй закон Ньютона — дифференциальный закон движения, описывающий взаимосвязь между приложенной к материальной точке силой и получающимся от этогоускорением этой точки. Фактически, второй закон Ньютона вводит массу как меру проявления инертности материальной точки в выбранной инерциальной системе отсчёта (ИСО).
Масса материальной точки при этом полагается величиной постоянной во времени и независящей от каких-либо особенностей её движения и взаимодействия с другими телами [4][5][6][7] .
Современная формулировка[править | править вики-текст]
| В инерциальной системе отсчёта ускорение, которое получает материальная точка с постоянной массой, прямо пропорционально равнодействующей всех приложенных к ней сил и обратно пропорционально её массе. |
При подходящем выборе единиц измерения, этот закон можно записать в виде формулы:
где 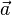
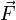
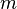
Второй закон Ньютона может быть также сформулирован в эквивалентной форме с использованием понятия импульс:
В инерциальной системе отсчета скорость изменения импульса материальной точки равна равнодействующей всех приложенных к ней внешних сил. 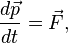 |
где 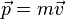
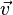
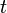
Иногда предпринимаются попытки распространить сферу применения уравнения 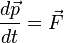
Замечания[править | править вики-текст]
Когда на материальную точку действуют несколько сил, с учётом принципа суперпозиции, второй закон Ньютона записывается в виде:
Второй закон Ньютона, как и вся классическая механика, справедлив только для движения тел со скоростями, много меньшими скорости света. При движении тел со скоростями, близкими к скорости света, используется релятивистское обобщение второго закона, получаемое в рамках специальной теории относительности.
Следует учитывать, что нельзя рассматривать частный случай (при 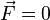
В уравнении движения динамической системы входит полный набор переменных, определяющий состояние этой системы (например, все координаты и скорости, или все координаты и импульсы), а также их производные по времени, что позволяет, зная такой набор в некий момент времени, вычислить его для момента времени, отстоящего на малый (бесконечно малый) промежуток времени. В принципе, повторяя этот процесс вычисления последовательно большое (бесконечное) количество раз, можно вычислить значение всех этих переменных для момента времени, как угодно далеко [2] отстоящего от начального. С помощью такого процесса можно (выбрав 
В современной квантовой теории термин уравнение движения нередко используется для обозначения именно только классических уравнений движения, то есть как раз для различения классического и квантового случая. В таком употреблении, например, слова «решение уравнений движения» означают именно классическое (неквантовое) приближение, которое может затем так или иначе использоваться при получении квантового результата или для сравнения с ним. В этом смыслеуравнения эволюции волновой функции не называют уравнениями движения, например упомянутые ниже уравнение Шредингера и уравнение Дирака нельзя назвать уравнением движения электрона. Определённую ясность тут вносит дополнение, указывающее на то, об уравнении движения чего идёт речь: так, хотя уравнение Дирака нельзя назвать уравнением движения электрона, его можно, даже в смысле, обсуждаемом в этом абзаце, назвать классическим уравнением движения спинорного поля.
| | | следующая лекция ==> |
| д) Исполнительные двигатели постоянного тока. | | |
Дата добавления: 2016-01-29 ; просмотров: 4544 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Видео:Мастер-класс по физике. Динамические характеристики движенияСкачать

Силовые характеристики движений
Лекция № 5
Динамические характеристики движений
- Общий обзор динамических характеристик и их классификация.
- Инерционные характеристики движений
- Силовые характеристики движений
- Энергетические характеристики движений
Общий обзор динамических характеристик и их классификация.
Динамические характеристики движенийраскрывают причины движения в связи с силами, приложенными к движущимся объектам.
Динамика решает 2 задачи:
1) как изменяется движение тела при действии на него данной силы.
2) какие силы действовали на данное движущееся тело.
К динамическим характеристикам относят:
1) инерционные характеристики– особенности тела человека и движимых им тел;
2) силовые характеристики– особенности взаимодействия звеньев тела и других тел;
3) энергетические характеристики– состояния и изменения работоспособности биомеханических систем
Динамические характеристики связаны с з основными законами механики,которые впервые изложил английский ученый И. Ньютон (1643-1727 гг) в своем главном труде «Математические начала естественной философии»
| Динамические характеристики движений | ||||||||||
| ↓ | ↓ | ↓ | ||||||||
| инерционные | силовые | эергетические | ||||||||
| ↓ | ↓ | ↓ | ↓ | ↓ | ↓ | ↓ | ↓ | ↓ | ↓ | ↓ |
| инертность | масса | момент инерции | сила | момент силы | импульс | импульс момента силы | работа силы | мощность силы | кинетическая энергия | потенциальная энергия |
Инерционные характеристики движений
Инертность (инерция) – свойство физических тел, проявляющееся в сохранении движения, а также изменении его под действием сил.
Движение, совершаемое материальной точкой при отсутствии сил, называется движением по инерции.
Закон инерции (1 закон Ньютона) указывает на одно из основных свойств материи – пребывать неизменно в движении. Состояние покоя рассматривается как частный случай движения по инерции, когда скорость равна 0.
Сохранение скорости неизменной (движение как бы по инерции) в реальных условиях возможно только тогда, когда все внешние силы, приложенные к телу, взаимно уравновешены. Это выражается формулой: а = 0, если F = 0.
Масса тела – это мера инертности тела при поступательном движении. Она измеряется отношением величины приложенной силы к вызываемому ею ускорению:
а − ускорение, F – сила.
Измерение массы тела в данном случае основано на 2 законе Ньютона: «изменение движения прямо пропорционально извне действующей силе и происходит по тому направлению, по которому эта сила приложена».
Масса тела во время движения не изменяется. При движении увеличивается или уменьшается не масса тела (мера инертности), а кинетическая энергия, зависящая от скорости тела.
Момент инерции – мера инертности тела при вращательном движении.
Момент инерции относительно данной оси численно равен сумме произведения масс всех его частей (звеньев) и квадратов расстояний каждой части тела до этой оси:
С моментом инерции связан момент количества движения, равный произведению момента инерции на угловую скорость.
Таким образом, угловая скорость тела зависит от расстояния (радиусов) его частей до оси вращения. Когда части тела находятся дальше от оси вращения, то угловое ускорение тела под действием того же момента силы меньше по сравнению с положением, когда части тела ближе к оси вращения.
Силовые характеристики движений
Силовые характеристикидвижений раскрывают связь действия силы с изменением движений.
Сила – это мера механического действия одного тела на другое.
Измерение силы (как и массы) основано на 2 законе Ньютона. Численно сила определяется произведением массы тела на его ускорение:
Таким образом, имеется «действие» второго тела на первое и «противодействие» первого тела.
Согласно 3 закону Ньютона: «действию всегда существует равное и противоположно направленное противодействие».
Момент силы – мера вращательного действия силы на тело.
Момент силы определяется произведением силы на ее плечо:
Момент силы считают положительным, когда сила вызывает поворот тела против часовой стрелки, и отрицательным при повороте тела по часовой стрелке (со стороны наблюдателя).
Говоря о силе тяги мышц, правильнее говорить о моменте силы мышц.
Импульс силы – мера воздействия силы на тело за данный промежуток времени (в поступательном движении).
Импульс силы равен произведению силы и продолжительности ее действия:
Импульс силы определяет прирост линейной скорости, тогда как силой обусловливается только ускорение.
Импульс момента силы – мера воздействия момента силы относительно данной оси за данный промежуток времени (во вращательном движении).
Импульс момента силы определяет изменение угловой скорости:
Pz – импульс момента силы Мz – момент силы ∆ t – промежуток времени.
📽️ Видео
10 класс - Физика - Кинематические и динамические характеристики движенияСкачать

Уравнения и графики механических гармонических колебаний. 11 класс.Скачать

Вращательное движение. 10 класс.Скачать

Вязкость. Ламинарное и турбулентное течения жидкостей. 10 класс.Скачать

Динамические уравнения ЭйлераСкачать

Урок 93. Основное уравнение динамики вращательного движенияСкачать

Урок 7. Механическое движение. Основные определения кинематики.Скачать

Основные уравнения движенияСкачать

МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ период колебаний частота колебанийСкачать

Лекция 12. Классификация режимов работы УМ по напряженности. Динамические характеристики (Ч.1)Скачать

Типовые динамические звенья | Вечер с теорией управления, вебинар 3Скачать

Лекция 06 Динамика твердого телаСкачать

Физика - перемещение, скорость и ускорение. Графики движения.Скачать

17) ТАУ для чайников. Пример определения статических и динамических характеристик элемента АСУ. Ч.1Скачать

ФИЗИКА ЕГЭ 2021. Кинематика. Графики движения. Часть 1.Скачать

Урок 15. Решение задач на графики движенияСкачать

Теория механизмов и машин. Лекция: динамические модели механизмов и определение их параметровСкачать

Урок 12. Равномерное прямолинейное движениеСкачать