Дифференциальные уравнения модель хищник жертва

Видео:Лабораторная работа №5. Модель хищник-жертва.Скачать

Модели взаимодействия двух видов

Гипотезы Вольтерра. Аналогии с химической кинетикой. Вольтерровские модели взаимодействий. Классификация типов взаимодействий Конкуренция. Хищник-жертва. Обобщенные модели взаимодействия видов . Модель Колмогорова. Модель взаимодействия двух видов насекомых Макартура. Параметрический и фазовые портреты системы Базыкина.

Основателем современной математической теории популяций справедливо считается итальянский математик Вито Вольтерра, разработавший математическую теорию биологических сообществ, аппаратом которой служат дифференциальные и интегро-дифференциальные уравнения. (Vito Volterra. Lecons sur la Theorie Mathematique de la Lutte pour la Vie. Paris , 1931). В последующие десятилетия популяционная динамика развивалась, в основном, в русле высказанных в этой книге идей. Русский перевод книги Вольтерра вышел в 1976 г. под названием: «Математическая теория борьбы за существование» с послесловием Ю.М. Свирежева, в котором рассматривается история развития математической экологии в период 1931‑1976 гг.

Книга Вольтерра написана так, как пишут книги по математике. В ней сначала сформулированы некоторые предположения о математических объектах, которые предполагается изучать, а затем проводится математическое исследование свойств этих объектов.

Системы, изученные Вольтерра, состоят их двух или нескольких видов. В отдельных случаях рассматривается запас используемой пищи. В основу уравнений, описывающих взаимодействие этих видов, положены следующие представления.

1. Пища либо имеется в неограниченном количестве, либо ее поступление с течением времени жестко регламентировано.

2. Особи каждого вида отмирают так, что в единицу времени погибает постоянная доля существующих особей.

3. Хищные виды поедают жертв, причем в единицу времени количество съеденных жертв всегда пропорционально вероятности встречи особей этих двух видов, т.е. произведению количества хищников на количество жертв.

4. Если имеется пища в ограниченном количестве и несколько видов, которые способны ее потреблять, то доля пищи, потребляемой видом в единицу времени, пропорциональна количеству особей этого вида, взятому с некоторым коэффициентом, зависящим от вида (модели межвидовой конкуренции).

5. Если вид питается пищей, имеющейся в неограниченном количестве, прирост численности вида в единицу времени пропорционален численности вида.

6. Если вид питается пищей, имеющейся в ограниченном количестве, то его размножение регулируется скоростью потребления пищи, т.е. за единицу времени прирост пропорционален количеству съеденной пищи.

Аналогии с химической кинетикой

Эти гипотезы имеют близкие параллели с химической кинетикой. В уравнениях популяционной динамики, как и в уравнениях химической кинетики, используется “принцип соударений”, когда скорость реакции пропорциональна произведению концентраций реагирующих компонентов.

Действительно, согласно гипотезам Вольтерра, скорость процесса отмирания каждого вида пропорциональна численности вида. В химической кинетике это соответствует мономолекулярной реакции распада некоторого вещества, а в математической модели – отрицательным линейным членам в правых частях уравнений.

Согласно представлениям химической кинетики, скорость бимолекулярной реакции взаимодействия двух веществ пропорциональна вероятности столкновения этих веществ, т.е. произведению их концентрации. Точно так же, в соответствии с гипотезами Вольтерра, скорость размножения хищников (гибели жертв) пропорциональна вероятности встреч особей хищника и жертвы, т.е. произведению их численностей. И в том и в другом случае в модельной системе появляются билинейные члены в правых частях соответствующих уравнений.

Наконец, линейные положительные члены в правых частях уравнений Вольтерра, отвечающие росту популяций в неограниченных условиях, соответствуют автокаталитическим членам химических реакций. Такое сходство уравнений в химических и экологических моделях позволяет применить для математического моделирования кинетики популяций те же методы исследований, что и для систем химических реакций.

Классификация типов взаимодействий

В соответствии с гипотезами Вольтерра взаимодействие двух видов, численности которых x₁ и x₂, могут быть описаны уравнениями:

(9.1)

Здесь параметры a _i ‑ константы собственной скорости роста видов, c _i ‑ константы самоограничения численности (внутривидовой конкуренции), b_ij ‑ константы взаимодействия видов, ( i , j=1,2). Знаки этих коэффициентов определяют тип взаимодействия.

В биологической литературе обычно классифицируют взаимодействия по участвующим в них механизмам. Разнообразие здесь огромно: различные трофические взаимодействия, химические взаимодействия, существующие между бактериями и планктонными водорослями, взаимодействия грибов с другими организмами, сукцессии растительных организмов, связанные в частности, с конкуренцией за солнечный свет и с эволюцией почв и т.д. Такая классификация кажется необозримой.

E . Одум, учитывая предложенные В.Вольтерра модели, предложил классификацию не по механизмам, а по результатам. Согласно этой классификации, оценивать взаимоотношения следует как положительные, отрицательные или нейтральные в зависимости от того, возрастает, убывает или остается неизменной численность одного вида в присутствии другого вида. Тогда основные типы взаимодействий могут быть представлены в виде таблицы.

ТИПЫ ВЗАИМОДЕЙСТВИЯ ВИДОВ

В последнем столбце указаны знаки коэффициентов взаимодействия из системы (9.1)

Рассмотрим основные типы взаимодействий

Как мы уже видели в лекции 6, уравнения конкуренции имеют вид:

(9.2)

Стационарные решения системы:

(1).

Начало координат, при любых параметрах системы представляет собой неустойчивый узел.

(2). (9.3)

C тационарное состояние (9.3) представляет собой седло при a₁ >b₁₂ / с₂ и

устойчивый узел при a₁ /с₂ . Это условие означает, что вид вымирает, если его собственная скорость роста меньше некоторой критической величины.

(3). (9.4)

(4). (9.5)

Стационарное состояние (9.5) характеризует сосуществование двух конкурирующих видов и представляет собой устойчивый узел в случае выполнения соотношения:

Отсюда следует неравенство:

позволяющее сформулировать условие сосуществования видов:

Произведение коэффициентов межпопуляционного взаимодействия меньше произведения коэффициентов внутри популяционного взаимодействия.

Действительно, пусть естественные скорости роста двух рассматриваемых видов a ₁ , a ₂ одинаковы. Тогда необходимым для устойчивости условием будет

Эти неравенства показывают, что увеличение численности одного из конкурентов сильнее подавляет его собственный рост, чем рост другого конкурента. Если численность обоих видов ограничивается, частично или полностью, различными ресурсами, приведенные выше неравенства справедливы. Если же оба вида имеют совершенно одинаковые потребности, то один из них окажется более жизнеспособным и вытеснит своего конкурента.

Поведение фазовых траекторий системы дает наглядное представление о возможных исходах конкуренции. Приравняем нулю правые части уравнений системы (9.2):

При этом получим уравнения для главных изоклин системы

– уравнения изоклин вертикальных касательных.

– уравнения изоклин вертикальных касательных. Точки попарного пересечения изоклин вертикальных и горизонтальных касательных систем представляют собой стационарные решения системы уравнений (9.2.), а их координаты суть стационарные численности конкурирующих видов.

Возможное расположение главных изоклин в системе (9.2) изображено на рис.9.1. Рис. 9.1 а соответствует выживанию вида x ₁ , рис. 9.1 б – выживанию вида x ₂ , рис. 9.1 в – сосуществованию видов при выполнении условия (9.6). Рисунок 9.1 г демонстрирует триггерную систему. Здесь исход конкуренции зависит от начальных условий. Ненулевое для обоих видов стационарное состояние (9.5) – неустойчивое. Это – седло, через которое проходит сепаратриса, отделяющая области выживания каждого из видов.

Рис. 9.1. Расположение главных изоклин на фазовом портрете вольтерровской системы конкуренции двух видов (9.2) при разном соотношении параметров. Пояснения в тексте.

Для изучения конкуренции видов ставились эксперименты на самых различных организмах. Обычно выбирают два близкородственных вида и выращивают их вместе и по отдельности в строго контролируемых условиях. Через определенные промежутки времени проводят полный или выборочный учет численности популяции. Регистрируют данные по нескольким повторным экспериментам и анализируют. Исследования проводили на простейших (в частности, инфузориях), многих видах жуков рода Tribolium, дрозофиллах, пресноводных ракообразных (дафниях). Много экспериментов проводилось на микробных популяциях (см. лекция 11). В природе также проводили эксперименты, в том числе на планариях (Рейнольдс), двух видах муравьев (Понтин) и др. На рис. 9.2. изображены кривые роста диатомовых водорослей, использующих один и тот же ресурс (занимающих одну и ту же экологическую нишу). При выращивании в монокультуре Asterionella Formosa выходит на постоянный уровень плотности и поддержвает концентрацию ресурса (силиката) на постоянно низком уровне. Б. При выращивании в монокультуре Synedrauina ведет себя сходным образом и поддерживает концентрацию силиката на еще более низком уровне. В. При совместном культивировании (в двух повторностях) Synedrauina вытесняет Asterionella Formosa . По-видимому, Synedra выигрывает конкуренцию благодаря своей способности к более полному использованию субстрата (см. также Лекцию 11).

Рис. 9.2. Конкуренция у диатомовых водорослей. а ‑ при выращивании в монокультуре Asterionella Formosa выходит на постоянный уровень плотности и поддерживает концентрацию ресурса (силиката) на постоянно низком уровне. б ‑ при выращивании в монокультуре Synedrauina ведет себя сходным образом и поддерживает концентрацию силиката на еще более низком уровне. в ‑ при совместном культивировании (в двух повторностях) Synedruina вытесняет Asterionella Formosa . По-видимому, Synedra выигрывает конкуренцию благодаря своей способности к более полному использованию субстрата (см. также Лекцию 11).

Широко известны эксперименты по изучению конкуренции Г. Гаузе, продемонстрировавшие выживание одного из конкурирующих видов и позволившие ему сформулировать «закон конкурентного исключения». Закон гласит, что в одной экологической нише может существовать только один вид. На рис. 9.3. приведены результаты экспериментов Гаузе для двух видов Parametium , занимающих одну экологическую нишу (рис. 9.3 а, б) и видами, занимающими разные экологические ниши (рис. 9.3. в).

Рис. 9.3. а — Кривые роста популяций двух видов Parametium в одновидовых культурах. Черные кружки – P Aurelia , белые кружки – P . Caudatum

б — Кривые роста P Aurelia и P . Caudatum в смешанной культуре.

Модель конкуренции (9.2) имеет недостатки, в частности, из нее следует, что сосуществование двух видов возможно лишь в случае, если их численность ограничивается разными факторами, но модель не дает указаний, насколько велики должны быть различия для обеспечения длительного сосуществования. В то же время известно, что для длительного сосуществования в изменчивой среде необходимо различие, достигающее определенной величины. Внесение в модель стохастических элементов (например, введение функции использования ресурса) позволяет количественно исследовать эти вопросы.

Система ХИЩНИК+ЖЕРТВА

Для взаимоотношений типа хищник‑жертва или паразит‑хозяин система уравнений (9.1) принимает вид:

(9.7)

Здесь, в отличие от (9.2) знаки b₁₂ и b₂₁ — разные. Как и в случае конкуренции, начало координат

(9.8)

является особой точкой типа неустойчивый узел. Три других возможных стационарных состояния:

, (9.9)

(9.10)

(9.11)

Таким образом, возможно выживание только жертвы (9.10), только хищника (9.9) (если у него имеются и другие источники питания) и сосуществование обоих видов (9.11). Последний вариант уже был рассмотрен нами в лекции 5. Возможные типы фазовых портретов для системы хищник-жертва представлены на рис. 9.4.

Изоклины горизонтальных касательных представляют собой прямые

а изоклины вертикальных касательных – прямые

Стационарные точки лежат на пересечении изоклин вертикальных и горизонтальных касательных.

Рис. 9.4. Расположение главных изоклин на фазовом портрете вольтерровской системы хищник-жертва (9.7) при различных соотношениях параметров. Стрелками указано направление фазовых траекторий. Пояснения в тексте.

Из рис. 9.4 видно следующее. Система хищник – жертва (9.7) может иметь устойчивое положение равновесия, в кот o ром популяция жертв полностью вымерла ( ) и остались только хищники (точка 2 на рис. 9.4 а). Очевидно, такая ситуация может реализоваться лишь в случае, если кроме рассматриваемого вида жертв х₁ хищник х₂– имеет дополнительные источники питания. Этот факт в модели отражается положительным членом в правой части уравнения для х₂. Особые точки (1) и (3) (рис. 9.4 а ) являются неустойчивыми. Вторая возможность – устойчивое стационарное состояние, в котором популяция хищников полностью вымерла и остались одни жертвы – устойчивая точка (3) (рис. 9.4 6). Здесь особая точка (1) – также неустойчивый узел.

Наконец, третья возможность – устойчивое сосуществование популяций хищника и жертвы (рис. 9.4 в ), стационарные численности которых выражаются формулами (9.11).

Как и в случае одной популяции (см. Лекция 3), для модели (9.7) можно разработать стохастическую модель, но для нее нельзя получить решение в явном виде. Поэтому мы ограничимся общими рассуждениями. Допустим, например, что точка равновесия находится на некотором расстоянии от каждой из осей. Тогда для фазовых траекторий, на которых значения x ₁ , x ₂ остаются достаточно большими, вполне удовлетворительной будет детерминистическая модель. Но если в некоторой точке фазовой траектории какая–либо переменная не очень велика, то существенное значение могут приобрести случайные флюктуации. Они приводят к тому, что изображающая точка переместится на одну из осей, что означает вымирание соответствующего вида.

Таким образом, стохастическая модель оказывается неустойчивой, так как стохастический “дрейф” рано или поздно приводит к вымиранию одного из видов. В такого рода модели хищник в конечном счете вымирает, это может произойти либо случайно, либо вследствие того, что сначала элиминируется популяция его жертвы. Стохастическая модель системы хищник – жертва хорошо объясняет эксперименты Гаузе (Гаузе, 1934), в которых инфузория Paramettum candatum служила жертвой для другой инфузории Didinium nasatum – хищника. Ожидавшиеся согласно детерминистическим уравнениям (9.7) равновесные численности в этих экспериментах составляли примерно всего по пять особей каждого вида, так что нет ничего удивительного в том, что в каждом повторном эксперименте довольно быстро вымирали либо хищники, либо жертвы (а за ними и хищники) Результаты экспериментов представлены на рис. 9.5.

Рис . 9.5. Рост Parametium caudatum и хищной инфузории Dadinium nasutum . Из : Gause G.F. The struggle for existence. Baltimore , 1934

Итак, анализ вольтерровских моделей взаимодействия видов показывает, что, несмотря на большое разнообразие типов поведения таких систем, незатухающих колебаний численности в модели конкурирующих видов не может быть вовсе. Однако в природе и в эксперименте такие колебания наблюдаются. Необходимость их теоретического объяснения послужила одной из причин для формулировки модельных описаний в более общем виде.

Обобщенные модели взаимодействия двух видов

Было предложено большое число моделей, описывающих взаимодействие видов, правые части уравнений которых представляли собой функции численностей взаимодействующих популяций. Решался вопрос о выработке общих критериев, позволяющих установить, какого вида функции могут описать особенности поведения временного численности популяции, в том числе устойчивые колебания. Наиболее известные из этих моделей принадлежат Колмогорову (1935, переработанная статья ‑ 1972) и Розенцвейгу (1963).

А.Н.Колмогоров рассмотрел обобщенную модель взаимодействия биологических видов типа хищни‑жертва или паразит‑хозяин. Модель представляет собой систему двух уравнений общего вида

(9.12)

В модель заложены следующие предположения:

1) Хищники не взаимодействуют друг с другом, т.е. коэффициент размножения хищников k₂ и число жертв L, истребляемых в единицу времени одним хищником, не зависит от y.

2) Прирост числа жертв при наличии хищников равен приросту в отсутствие хищников минус число жертв, истребляемых хищниками. Функции k₁( x) , k₂ ( x) , L( x), ‑ непрерывны и определены на положительной полуоси x, y ³ 0.

3) dk₁ /dx . Это означает, что коэффициент размножения жертв в отсутствие хищника монотонно убывает с возрастанием численности жертв, что отражает ограниченность пищевых и иных ресурсов.

4) dk₂ / dx>0 , k₂ (0) ¥ ). С ростом численности жертв коэффициент размножения хищников монотонно убывает с возрастанием численности жертв, переходя от отрицательных значений, (когда нечего есть) к положительным.

5) Число жертв, истребляемых одним хищником в единицу времени L( x) >0 при N>0 ; L(0)=0.

Возможные типы фазовых портретов системы (9.12) представлены на рис. 9.6:

Рис. 9.6. Фазовые портреты системы Колмогорова (9.12), описывающей взаимодействие двух видов при разных соотношениях параметров. Пояснения в тексте.

Стационарные решения (их два или три) имеют следующие координаты:

Начало координат при любых значениях параметров представляет собой седло (рис. 9.6 а-г).

A определяется из уравнения:

Стационарное решение (9.13) ‑ седло, если B A (рис. 9.6 а, б , г ) , B определяется из уравнения

Точка (9.13) помещается в положительном квадранте, если B>A . Это ‑ устойчивый узел .

Последний случай, который соответствует гибели хищника и выживанию жертвы, представлен на рис. 9.6 в .

Величина С определяется из уравнений:

Точка (9.14) – фокус (рис.9.6 а) или узел (рис.9.6 г), устойчивость которых зависит от знака величины s

Если s >0 , точка устойчива, если s 9.6 б)

В зарубежной литературе чаще рассматривается сходная модель, предложенная Розенцвейгом и Макартуром (1963):

(9.15)

где f( x) — скорость изменения численности жертв x в отсутствие хищников, Ф( x,y) ‑ интенсивность хищничества, k ‑ коэффициент, характеризующий эффективность переработки биомассы жертвы в биомассу хищника, e — смертность хищника.

Модель (9.15) сводится к частному случаю модели Колмогорова (9.12) при следующих предположениях:

1) численность хищника ограничивается только численностью жертвы,

2) скорость, с которой данная особь хищника поедает жертву, зависит только от плотности популяции жертв и не зависит от плотности популяции хищников.

Тогда уравнения (9.15) принимают вид.

При описании взаимодействия реальных видов, правые части уравнений конкретизируются в соответствии с представлениями о биологических реалиях. Рассмотрим одну из самых популярных моделей такого типа.

Модель взаимодействия двух видов насекомых ( M acArthur, 1971)

Модель, которую мы рассмотрим ниже, использовалась для решения практической задачи борьбы с вредными насекомыми с помощью стерилизации самцов одного из видов. Исходя из биологических особенностей взаимодействия видов, была написана следующая модель

(9.16)

Здесь x,y — биомассы двух видов насекомых. Трофические взаимодействия описываемых в этой модели видов – весьма сложные. Этим определяется вид многочленов в правых частях уравнений.

Рассмотрим правую часть первого уравнения. Насекомые вида х поедают личинок вида у (член + k₃ y), но взрослые особи вида у поедают личинок вида х при условии высокой численности видов х или у или обоих видов (члены – k₄ xy, – у 2 ) . При малых х смертность вида х выше, чем его естественный прирост (1 –k₁ +k₂ x–x 2 при малых х). Во втором уравнении член k₅ отражает естественный прирост вида y; –k₆ y – самоограничение этого вида, –k ₇ x – поедание личинок вида у насекомыми вида х, k₈ xy – прирост биомассы вида у за счет поедания взрослыми насекомыми вида у личинок вида х.

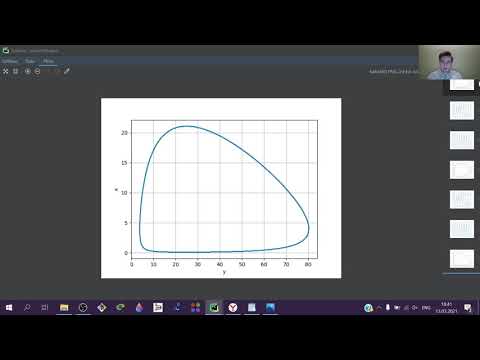
На рис. 9.7 представлен предельный цикл, являющийся траекторией устойчивого периодического решения системы (9.16).

Рис 9.7 . Фазовый портрет модели (9.16) (MacArthur, 1971)

Жирная замкнутая кривая – предельный цикл,

штрих-пунктир – изоклины вертикальных и горизонтальных касательных

Решение вопроса о том, каким образом обеспечить сосуществование популяции с ее биологическим окружением, разумеется, не может быть получено без учета специфики конкретной биологической системы и анализа всех ее взаимосвязей. Вместе с тем изучение формальных математических моделей позволяет ответить на некоторые общие вопросы. Можно утверждать, что для моделей типа (9.12) факт совместимости или несовместимости популяций не зависит от их начальной численности, а определяется только характером взаимодействия видов. Модель помогает ответить на вопрос: как следует воздействовать на биоценоз, управлять им, чтобы по возможности быстро уничтожить вредный вид.

Пусть популяция вредного вида совместима с окружающим биоценозом. Это означает, что существует устойчивый стационарный режим (устойчивая точка покоя или предельный цикл), описывающий динамику популяций хищника (паразита) и жертвы (хозяина). Введение управления в такую систему возможно в двух формах.

Управление может сводиться к кратковременному, скачкообразному изменению величин численности х и у. Такой способ отвечает методам борьбы типа однократного уничтожения одной или обеих популяций химическими средствами. Из сформулированного выше утверждения видно, что для совместимых популяций этот метод борьбы будет малоэффективным, поскольку с течением времени система опять выйдет на стационарный режим.

Другой способ ‑ изменение вида функций взаимодействия между видами, например, при изменении значений параметров системы. Именно такому, параметрическому, способу отвечают биологические методы борьбы. Так при внедрении стерилизованных самцов уменьшается коэффициент естественного прироста популяции. Если при этом мы получим другой тип фазового портрета, такой, где имеется лишь устойчивое стационарное состояние с нулевой численностью вредителя, управление приведет к желаемому результату – уничтожению популяции вредного вида. Интересно отметить, что иногда воздействие целесообразно применить не к самому вредителю, а к его партнеру. Какой из способов более эффективен, в общем случае сказать нельзя. Это зависит от имеющихся в распоряжении средств управления и от явного вида функций, описывающих взаимодействие популяций.

Модель А.Д.Базыкина

Теоретический анализ моделей взаимодействий видов наиболее исчерпывающе проведен в книге А.Д.Базыкина “Биофизика взаимодействующих популяций” (М., Наука, 1985).

Рассмотрим одну из изученных в этой книге моделей типа хищник-жертва.

(9.17)

Система (9.17) является обобщением простейшей модели хищник-жертва Вольтерра (5.17) с учетом эффекта насыщения хищников. В модели (5.17) предполагается, что интенсивность выедания жертв линейно растет с ростом плотности жертв, что при больших плотностях жертв не соответствует реальности. Для описания зависимости рациона хищника от плотности жертв могут быть выбраны разные функции. Наиболее существенно, чтобы выбранная функция с ростом x асимптотически стремилась к постоянному значению. В модели (9.6) использовалась логистическая зависимость. В модели Базыкина в роли такой функции выбрана гипербола x/(1 +px). Вспомним, что такой вид имеет формула Моно, описывающая зависимость скорость роста микроорганизмов от концентрации субстрата. Здесь в роли субстрата выступает жертва, а в роли микроорганизмов – хищник .

Система (9.17) зависит от семи параметров. Число параметров можно уменьшить с помощью замены переменных:

В новых безразмерных переменных система имеет вид

(9.18)

и зависит от четырех параметров.

Для полного качественного исследования необходимо разбить четырехмерное пространство параметров на области с различным типом динамического поведения, т.е. построить параметрический, или структурный портрет системы.

Затем надо построить фазовые портреты для каждой из областей параметрического портрета и описать бифуркации, происходящие с фазовыми портретами на границах различных областей параметрического портрета.

Построение полного параметрического портрета производится в виде набора “срезов” (проекций) параметрического портрета малой размерности при фиксированных значениях некоторых из параметров.

Параметрический портрет системы (9.18) при фиксированных g и малых e представлен на рис.9.8. Портрет содержит 10 областей с различным типом поведения фазовых траекторий.

Рис. 9.8. Параметрический портрет системы (9.18) при фиксированных g

Поведение системы при различных соотношениях параметров может быть существенно различным (рис.9.9). В системе возможны:

1) одно устойчивое равновесие (области 1 и 5);

2) один устойчивый предельный цикл (области 3 и 8);

3) два устойчивых равновесия (область 2)

4) устойчивый предельный цикл и неустойчивое равновесие внутри него (области 6, 7, 9, 10)

5) устойчивый предельный цикл и устойчивое равновесие вне его (область 4).

В параметрических областях 7, 9, 10 область притяжения равновесия ограничивается неустойчивым предельным циклом, лежащим внутри устойчивого. Наиболее интересно устроен фазовый портрет, соответствующий области 6 на параметрическом портрете. Детально он изображен на рис. 9.10.

Рис. 9.9. Набор фазовых портретов системы (9.18), возможных в конечной части первого квадранта и соответствующих областям 1 ‑ 10 параметрического портрета рис. 9.8 (Базыкин, 1985)

Область притяжения равновесия В₂ (заштрихована) представляет собой “улитку”, скручивающуюся с неустойчивого фокуса В₁. Если известно, что в начальный момент времени система находилась в окрестности В₁, то судить о том, придет ли соответствующая траектория в равновесие В₂ или на устойчивый предельный цикл, окружающий три точки равновесия С (седло), В₁ и В₂ можно лишь на основе вероятностных соображений.

Рис.9.10. Фазовый портрет системы 9.18 для параметрической области 6. Область притяжения В₂ заштрихована

На параметрическом портрете (9.7) имеются 22 различные бифуркационные границы, которые образуют 7 различных типов бифуркаций. Их изучение позволяет выявить возможные типы поведения системы при изменении ее параметров. Например, при переходе из области 1 в область 3 происходит рождение малого предельного цикла, или мягкое рождение автоколебаний вокруг единственного равновесия В. Аналогичное мягкое рождение автоколебаний, но вокруг одного из равновесий, а именно B₁ , происходит при пересечении границы областей 2 и 4. При переходе из области 4 в область 5 устойчивый предельный цикл вокруг точки B ₁ “лопается” на петле сепаратрис и единственной притягивающей точкой остается равновесие B ₂ и т.д.

Особый интерес для практики представляет, конечно, выработка критериев близости системы к бифуркационным границам. Действительно, биологам хорошо известно свойство “буферности”, или “гибкости”, природных экологических систем. Этими терминами обычно обозначают способность системы как бы поглощать внешние воздействия. Пока интенсивность внешнего воздействия не превышает некоторой критической величины, поведение системы не претерпевает качественных изменений. На фазовой плоскости это соответствует возвращению системы в устойчивое состояние равновесия или на устойчивый предельный цикл, параметры которого не сильно отличаются от первоначального. Когда же интенсивность воздействия превышает допустимую, система “ломается”, переходит в качественно иной режим динамического поведения, например просто вымирает. Это явление соответствует бифуркационному переходу.

Каждый тип бифуркационных переходов имеет свои отличительные особенности, позволяющие судить об опасности такого перехода для экосистемы. Приведем некоторые общие критерии, свидетельствующие о близости опасной границы. Как и в случае одного вида, если при уменьшении численности одного из видов происходит “застревание” системы вблизи неустойчивой седловой точки, что выражается в очень медленном восстановлении численности к начальному значению, значит, система находится вблизи критической границы. Индикатором опасности служит также изменение формы колебаний численностей хищника и жертвы. Если из близких к гармоническим колебания становятся релаксационными, причем амплитуда колебаний увеличивается, это может привести к потере устойчивости системы и вымиранию одного из видов.

Итак, мы рассмотрели автономные непрерывные математические модели, описывающие взаимодействие двух видов. Сделаем некоторые выводы. При моделировании биоценоза из двух видов система Вольтерра (9.1) дает возможность для описания устойчивого сосуществования видов в условиях конкуренции, симбиоза и хищничества (паразитизма). При попытке описать устойчивые колебания численности видов мы сталкиваемся с трудностями. Система уравнений (5.17), описывающая взаимодействия хищник-жертва без учета самоограничения численности популяций и имеющая особую точку типа центр, ‑ негрубая и, следовательно, неустойчива к случайным флуктуациям численности. Предельных же циклов, являющихся фазовыми траекториями устойчивых автоколебаний, система типа Вольтерра (9.1) иметь не может. Для получения предельных циклов в модельных системах приходится выходить за рамки гипотез Вольтерра и учитывать более тонкие эффекты взаимодействия между видами. Правые части уравнений при этом становятся существенно нелинейными.

Дальнейшее углубление математической теории взаимодействия видов идет по линии детализации структуры самих популяций и учета временных и пространственных факторов.

Колмогоров А.Н. Качественное изучение математических моделей динамики популяций. // Пороблемы кибернетики. М ., 1972, Вып .5.

MacArtur R. Graphycal analysis of ecological systems// Division of biology report Perinceton University. 1971

А.Д.Базыкин “Биофизика взаимодействующих популяций”. М., Наука, 1985.

В.Вольтерра: «Математическая теория борьбы за существование». М .. Наука , 1976

Видео:Лабораторная работа №5. Модель хищник-жертва (часть 1)Скачать

Я догоняю, ты убегаешь

Что такое модель Лотки-Вольтерры и как она помогает биологам

Могут ли сложные математические инструменты применяться в биологии? Могут, если биологи изучают сложные динамические системы, например взаимодействие разных видов животных в естественной среде. Американец Альфред Лотка и итальянец Вито Вольтерра разработали модель, позволяющую описывать, как будет меняться поголовье хищников и их травоядных жертв в зависимости от множества привходящих условий. Это наш второй материал о самых интересных дифференциальных уравнениях (с первым можно ознакомиться здесь). Если вы читаете нас с телефона, переключайте страницу на десктопную версию, так вы сможете увидеть интерактивный график целиком.

Изначально Альфред Лотка вообще не планировал создавать никаких математических моделей. Он собирался разработать новую предметную область — «физическую биологию» — и поэтому начиная с 1902 года стал публиковать небольшие статьи, посвященные этой теме.

Параллельно с этим его все более интересовало применение математических методов в биологии. Идеи Лотки, однако, не получили широкого распространения — в то время американский ученый не имел широких связей в научной среде и работал в одиночестве.

Ситуация изменилась в 1920 году, когда статьи Лотки привлекли внимание биолога и статистика Раймонда Пирла, который нашел в них близкие для себя идеи: Пирл интересовался ростом популяции в пределах одного вида.

Лотка написал еще одну статью, и Пирл помог продвинуть ее в Proceedings of the National Academy of Sciences (ведущий американский журнал для публикации оригинальных научных исследований в различных областях). В этой статье Лотка в качестве примера описал взаимодействие растения и травоядного и пришел к неожиданному для него результату: их взаимодействие приведет к бесконечному циклическому колебанию в двух популяциях!

Позже Лотка расширил это наблюдение до общего случая взаимодействия типа «хищник-жертва».

Итальянский ученый Вито Вольтерра, как и Альфред Лотка, пришел к этой модели со стороны точных наук. Он с раннего детства питал тягу к математике и занимался ею всю свою жизнь, и уже в 1900-е годы заинтересовался возможностью использовать математику в биологии и общественных науках.

После окончания Первой мировой войны Вольтерра погрузился в биологию и, сам того не зная, пришел к выводам, схожим с выводами Альфреда Лотки, сделанными ранее. Однако именно работы Вольтерры привлекли внимание математического сообщества.

В итоге Вольтерра, чья статья вышла в 1926 году, признал приоритет Лотки. Но чтобы его собственные работы не выглядели бессмысленными, Вольтерра отметил, что рассмотрел ситуацию в более общем случае: вывел уравнения, которые описывают взаимодействие более чем двух видов и учитывают их контакт в прошлом.

Модель Лотки-Вольтерры

Система Лотки-Вольтерры является первоначальной и простейшей системой (усложненные системы будут рассмотрены ниже) для описания модели «хищник-жертва», то есть популяции хищников и популяции жертв, взаимодействующих в какой-то среде: жертвы едят растительность, хищники — жертв:

Видео:Рубин А. Б. - Биофизика I - Базовая модель «Хищник-жертва»Скачать

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ХИЩНИКИ-ЖЕРТВЫ

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ «ХИЩНИКИ-ЖЕРТВЫ»

Материальные и информационные модели
1. Биологические предметные модели, служат для изучения общих биологических закономерностей, действий различных препаратов, методов лечения. К этому типу моделей относятся лабораторные животные, изолированные органы, культуры клеток. Этот вид моделирования, самый древний и играет большую роль в современной науке(первые полеты в космос, испытание новых лекарств и т. д.)

2. Физические (аналоговые) модели − это физические системы или устройства, которые обладают аналогичным с моделируемым объектом поведением. Физическая модель может быть реализована в виде некоторого механического устройства или в виде электрической цепи. Например, процесс движения крови по крупным сосудам может быть смоделирован электрической цепью из конденсаторов и сопротивлений.

3. Кибернетические модели − это различные устройства, в составе которых имеется блок управления − чаще всего компьютер, который моделирует информационные процессы в живом организме, среди которых самый распространенный − это управление. (Например, управление движением руки, всего тела или управление величиной зрачка). Сложность таких кибернетических моделей разная, вплоть до “искусственного интеллекта”, являющегося кибернетической моделью мозга человека.

4. Математическая модель – это система математических соотношений – формул, уравнений, неравенств и т.д., отражающих существенные свойства объекта или явления.

Этапы математического моделирования
1этап: создание основы математической модели. При этом нужно-
а) накопить экспериментальные данные о процессах в изучаемой системе,
б) составить уравнение или систему уравнений, описывающих закономерную связь данных.

2 этап: проверка и корректировка модели. При этом необходимо:
а) определить численные значения коэффициентов и задать начальные условия,
б) решить систему уравнений,
в) сравнить полученное решение с данными эксперимента, выявить несоответствия, выяснить их причины,
г) ввести поправки в математическую модель.

3 этап: исследование математической модели, т.е. использование ее в практических целях
Конечной целью этого этапа является получение новой информации об исследуемом объекте.

Математическая модель “хищники — жертвы”
Впервые в биологии математическая модель периодического изменения числа особей антагонистических видов животных предложил итальянский математик В. Вольтерра с сотрудниками. Модель, предложенная Вольтерра, явилась развитием идеи, намеченной в 1924 году А. Лоттки в книге “Элементы физической биологии”. Поэтому данная классическая модель известна как “модель Лоттки-Вольтерра”.

Исходная задача
В некотором, экологически замкнутом районе, живут два вида животных (например, рыси и зайцы). Рыси (хищники) могут питаться только зайцами.

Исходная задача
Зайцы (жертвы) питаются растительной пищей, имеющейся всегда в достаточном количестве (в рамках данной модели не учитывается ограниченность ресурсов растительной пищи).

Исходная задача
Необходимо определить, как будет меняться численность жертв и хищников с течением времени в такой экологической системе.

Составление дифференциальных уравнений

Обозначим число жертв через N,
а число хищников через M.
Числа N и M являются функциями времени t.

В нашей модели учтем следующие факторы:
Естественное размножение жертв
Естественная гибель жертв
Уничтожение жертв за счет поедания их хищниками
Естественное вымирание хищников
Увеличение числа хищников за счет размножения при наличии пищи.

Так как речь идет о математической модели, то задачей является получение уравнений, в которые бы входили все намеченные факторы и которые описывали бы динамику, т.е. изменение числа хищников и жертв со временем.

Пусть за некоторое время ∆t количество жертв и хищников изменится на ∆N и ∆М. Изменение числа жертв ∆N за время ∆t определяется, во-первых, увеличением в результате естественного размножения (которое пропорционально количеству жертв);
(∆N)1=А N ∆t

(∆N)1=А N ∆t
где А — коэффициент пропорциональности, характеризующий скорость размножения жертв в данных условиях.

Во-вторых, имеет место уменьшение числа жертв из-за естественного вымирания, тоже пропорциональное их числу в данный момент:
(∆N)2= – В N ∆t
знак минус отражает именно уменьшение.

В основе вывода уравнения, описывающего уменьшение числа жертв из-за поедания их хищниками лежит идея о том , что чем чаще происходят их встречи , тем быстрее уменьшается число жертв.

Частота встреч хищника с жертвой пропорциональна и числу жертв и числу хищников, т.е. их произведению М·N

Поэтому можно записать:
(∆N)3= – C·M·N·∆t
Здесь коэффициент С характеризует частоту встреч жертвы с хищником.

В итоге с учетом всех трех факторов для изменения числа жертв можно записать следующее уравнение:
∆N=А·N·∆t – B·N·∆t – C·M·N·∆t

Поделив левую и правую часть уравнения на ∆t и перейдя к пределу при ∆t→0,
получим дифференциальное уравнение первого порядка:
dN/dt=A·N – B·N – C·M·N

Отметим, что левая часть уравнения является по смыслу “скоростью изменения числа жертв”, так как определяется как “изменение числа жертв ∆N за единицу времени ∆t.

Для того, чтобы решить это уравнение, нужно знать, как меняется число хищников М со временем.

Изменение числа хищников ∆M определяется увеличением из-за естественного размножения при наличии достаточного количества пищи ∆М1=Q·N·M·∆t
И уменьшением из-за естественного вымирания хищников
∆М2=-P·M·∆t

В итоге с учетом двух факторов для изменения числа хищников можно записать следующее уравнение:
∆М=Q·N·M·∆t — P·M·∆t

Поделив левую и правую часть уравнения на ∆t и перейдя к пределу при ∆t→0,
получим дифференциальное уравнение первого порядка
dM/dt=Q·M·N — P·M

Уравнения математической модели
dN/dt =A·N – B·N – C·M·N

Данные дифференциальные уравнения представляют собой математическую модель “хищники — жертвы”. Достаточно определить значения коэффициентов А, В, С, Q, P и математическую модель можно использовать для решения поставленной задачи.

Проверка и корректировка математической модели
N, M
N
M
t
1845
1930

1 уровень- в модели учтено для “жертв” только их естественное размножение. Хищники отсутствуют.
dN/dt =A·N

2 уровень — в модели учтены для “жертв “их естественное вымирание. Хищники отсутствуют.
dN/dt =-B·N

3 уровень — в модели учтены для “жертв” их естественное размножение и вымирание. Хищники отсутствуют
dN/dt =A·N-B·N

4 уровень — в модели учтены для “жертв” их естественное размножение и вымирание, а так же поедание “хищниками”, но число “хищников” считается неизменным
dN/dt =A·N-B·N-C·M·N

5 уровень — в модели учтены все обсуждавшиеся ранее факторы
dN/dt =A·N – B·N – C·M·N

Спасибо
за внимание!

Курс повышения квалификации

Охрана труда

• Сейчас обучается 106 человек из 42 регионов

Курс профессиональной переподготовки

Охрана труда

• Сейчас обучается 228 человек из 54 регионов

Курс профессиональной переподготовки

Библиотечно-библиографические и информационные знания в педагогическом процессе

• Сейчас обучается 354 человека из 63 регионов

Ищем педагогов в команду «Инфоурок»

Видео:ПР ПопуляцияСкачать

Дистанционные курсы для педагогов

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 566 207 материалов в базе

Другие материалы

• 07.11.2020
• 100
• 0

• 27.10.2020
• 122
• 0

• 09.10.2020
• 258
• 0

• 10.09.2020
• 620
• 1

• 22.08.2020
• 107
• 0

• 22.07.2020
• 178
• 1

• 14.07.2020
• 97
• 0

• 28.06.2020
• 456
• 12

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 04.02.2020 890
• PPTX 165.5 кбайт
• 13 скачиваний
• Оцените материал:

Настоящий материал опубликован пользователем Фефелова Татьяна Викторовна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 1 год и 1 месяц
• Подписчики: 0
• Всего просмотров: 25623
• Всего материалов: 225

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:Абдулов Тимур. Этапы построения математической модели. Реализация математической моделиСкачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Тринадцатилетняя школьница из Индии разработала приложение против буллинга

Время чтения: 1 минута

ЕГЭ в 2022 году будут сдавать почти 737 тыс. человек

Время чтения: 2 минуты

В России могут объявить Десятилетие науки и технологий

Время чтения: 1 минута

В Египте нашли древние школьные «тетрадки»

Время чтения: 1 минута

Профессия педагога на третьем месте по популярности среди абитуриентов

Время чтения: 1 минута

Объявлен конкурс дизайн-проектов для школьных пространств

Время чтения: 2 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

📹 Видео

Динамика биологических популяций 2Скачать

Сергеев И. Н. - Дифференциальные уравнения II - Фазовые пространства малых размерностейСкачать

Дифференциальные уравнения. 11 класс.Скачать

Видеоурок в 11 классе "Математические модели в биологии"Скачать

Лукьяненко Д. В. - Дифференциальные уравнения - Лекция 1Скачать

Лабораторная работа №5. Модель хищник-жертва (часть 2)Скачать

6.1 Численные методы решения задачи Коши для ОДУСкачать

Информатика 11 класс (Урок№10 - Математические модели. Стохастические модели.)Скачать

Семинар "Пространственно-временная динамика системы хищник-жертва с идеальным свободным..."Скачать

18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать