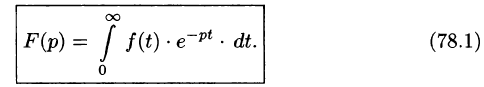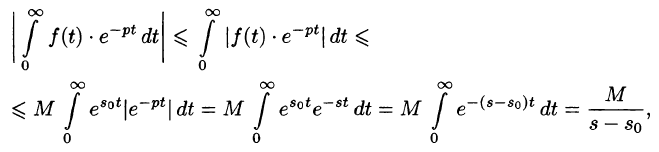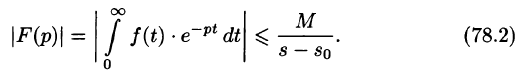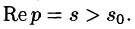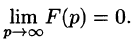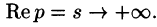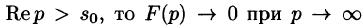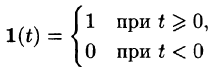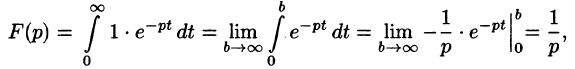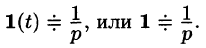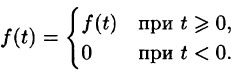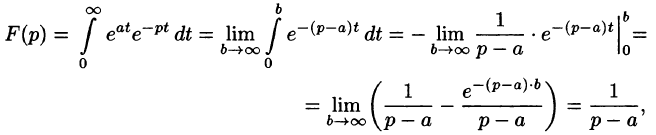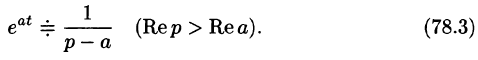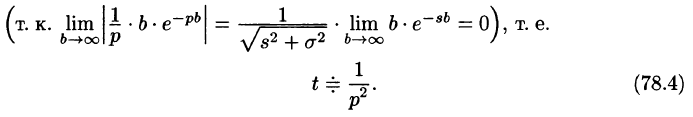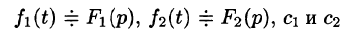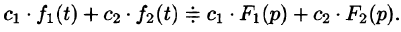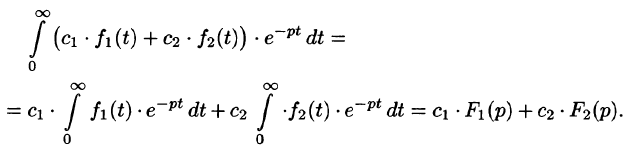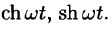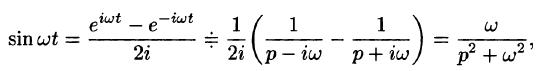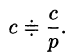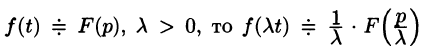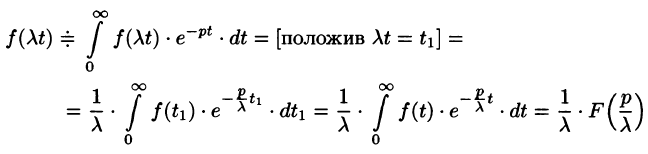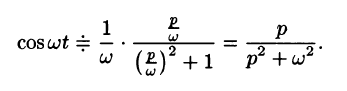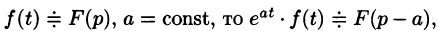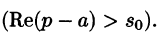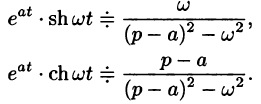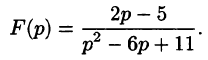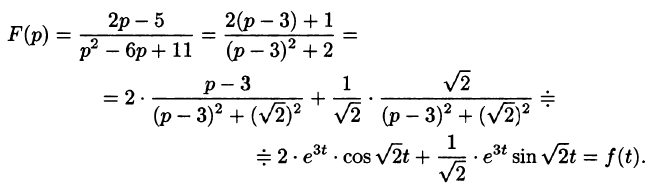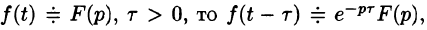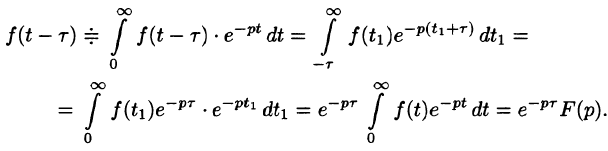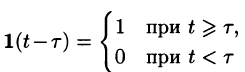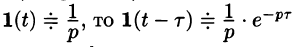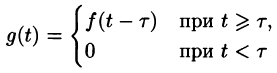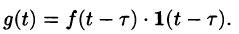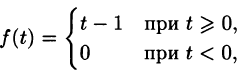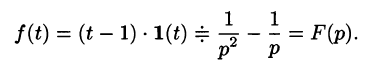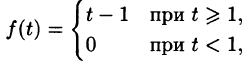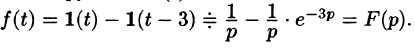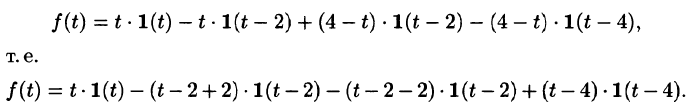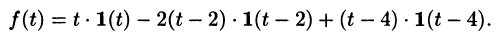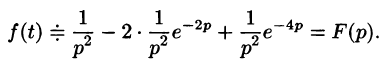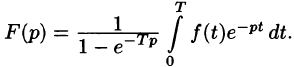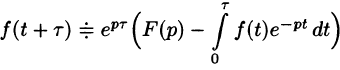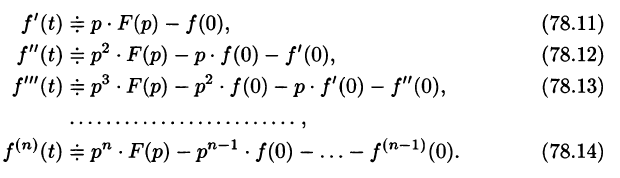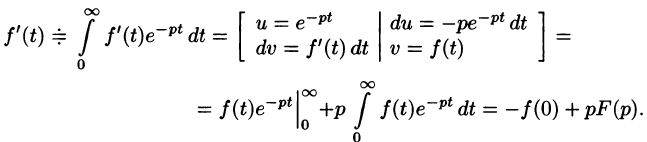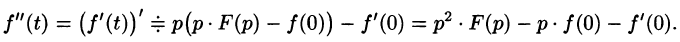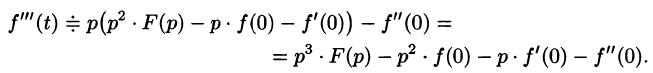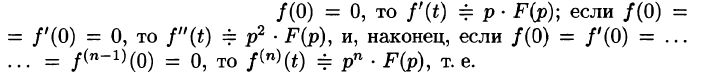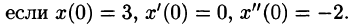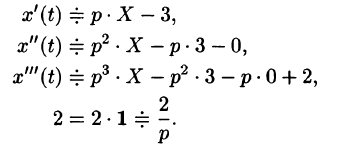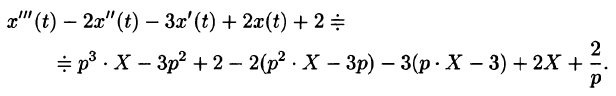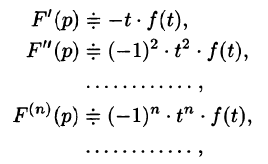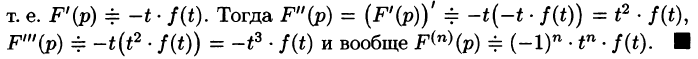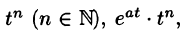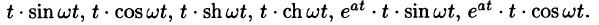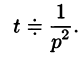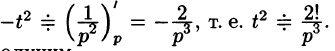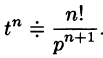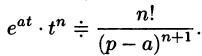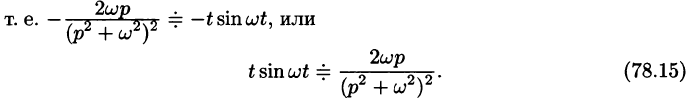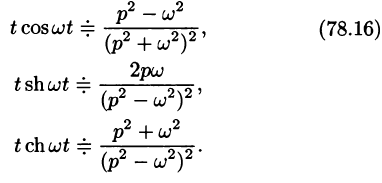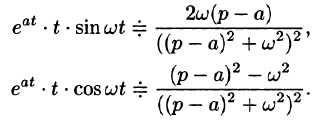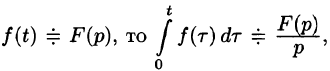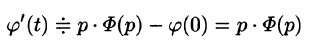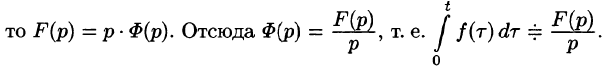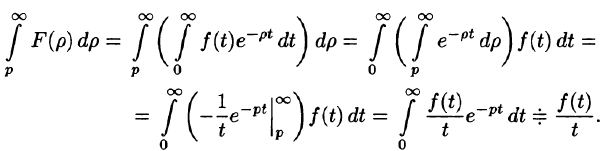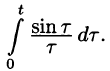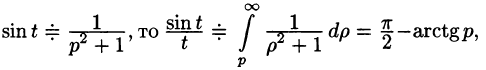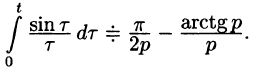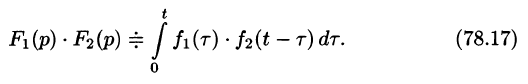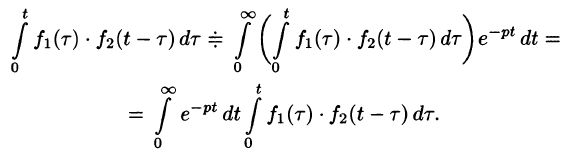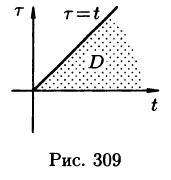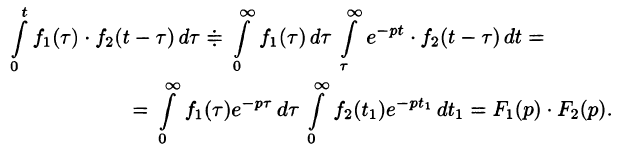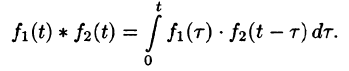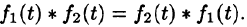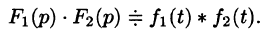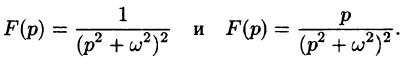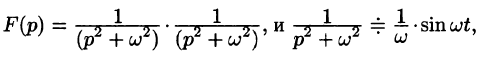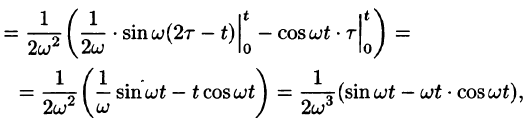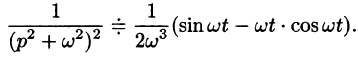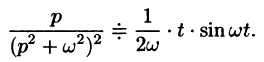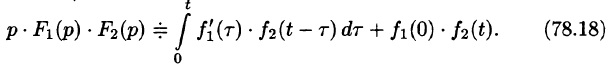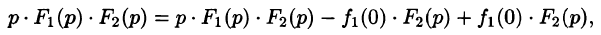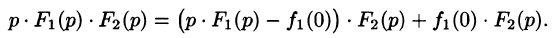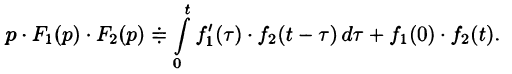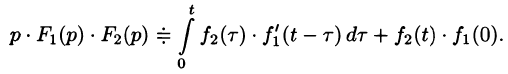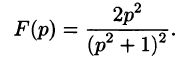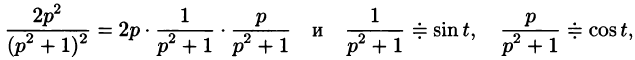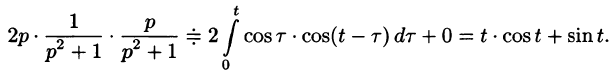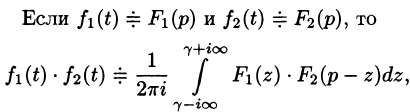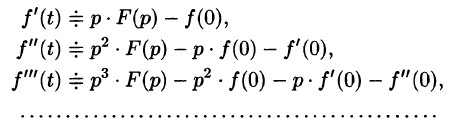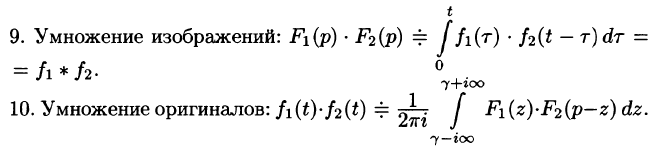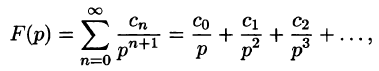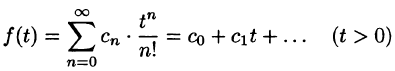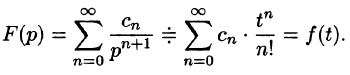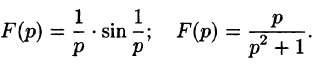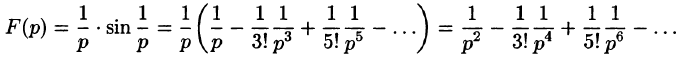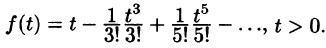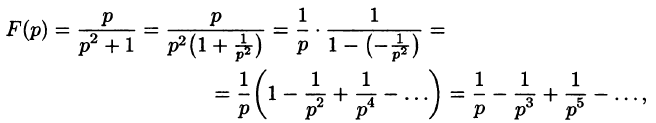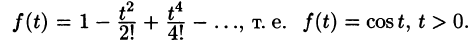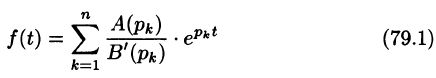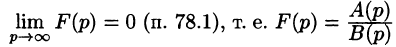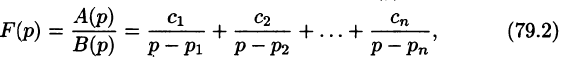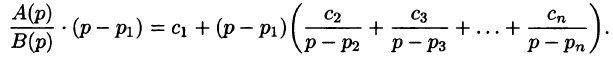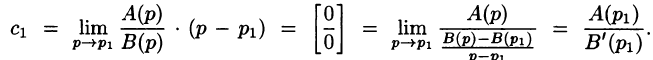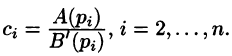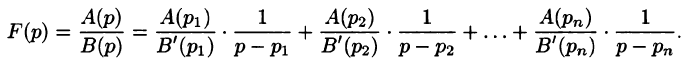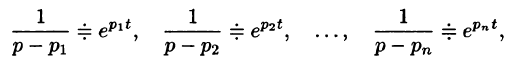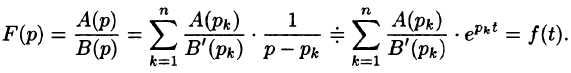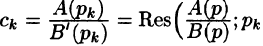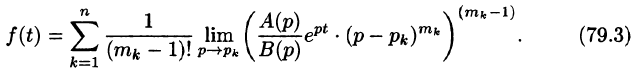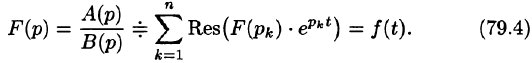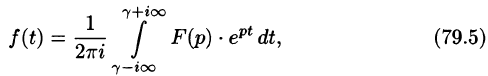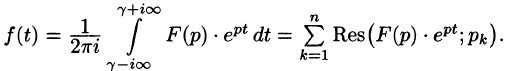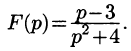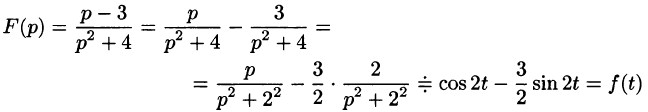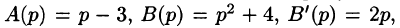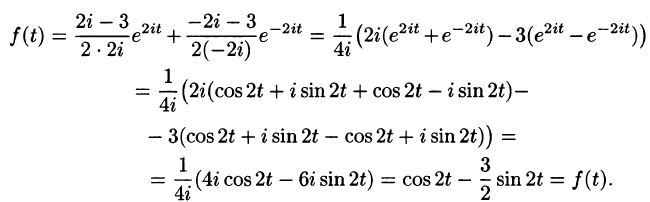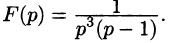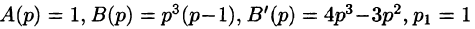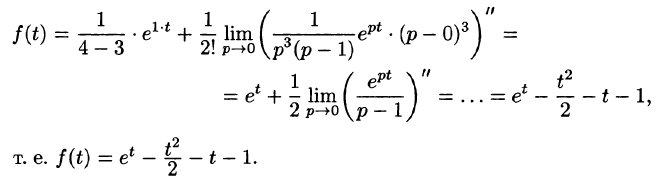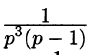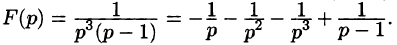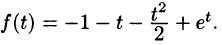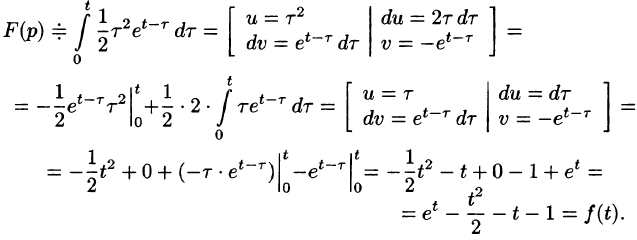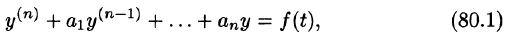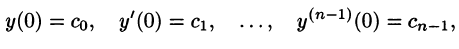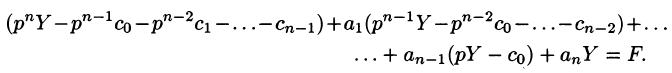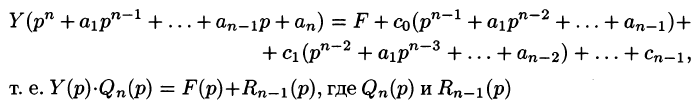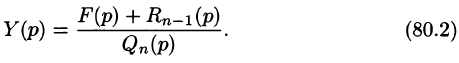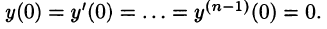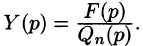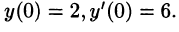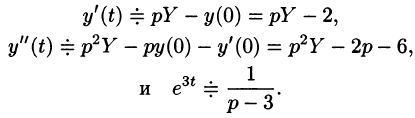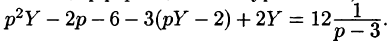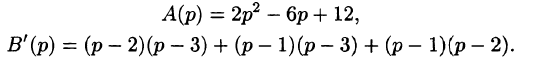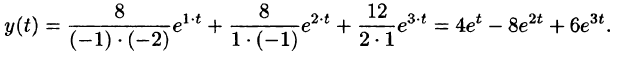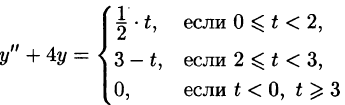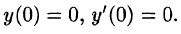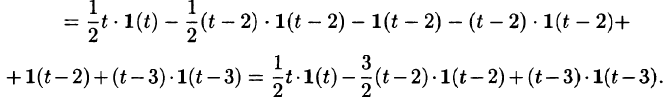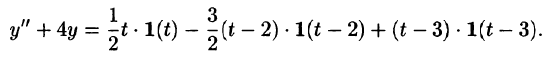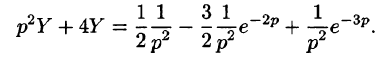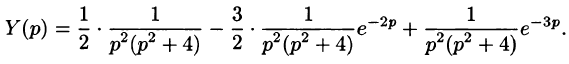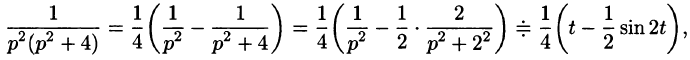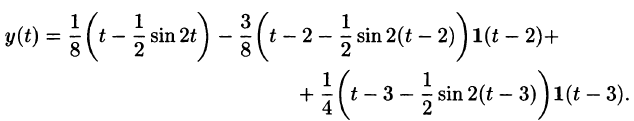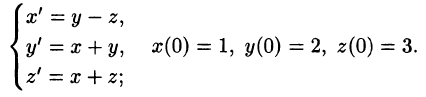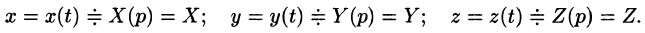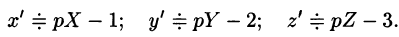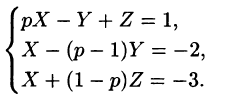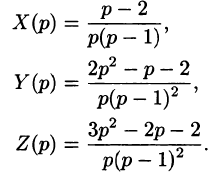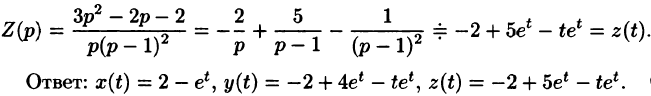Операционное исчисление играет важную роль при решении прикладных задач, особенно в современной автоматике и телемеханике.
Операционное исчисление — один из методов математического анализа, позволяющий в ряде случаев сводить исследование дифференциальных и некоторых типов интегральных операторов и решение уравнений, содержащих эти операторы, к рассмотрению более простых алгебраических задач.
Методы операционного исчисления предполагают реализацию следующей условной схемы решения задачи.
- От искомых функций переходят к некоторым другим функциям — их изображениям.
- Над изображениями производят операции, соответствующие заданным операциям над самими функциями.
- Получив некоторый результат при действиях над изображениями, возвращаются к самим функциям.
В качестве преобразования, позволяющего перейти от функции к их изображениям, будем применять так называемое преобразование Лапласа.
- Преобразование Лапласа
- Свойства преобразования Лапласа
- Линейность
- Смещение (затухание)
- Запаздывание
- Дифференцирование оригинала
- Дифференцирование изображения
- Интегрирование оригинала
- Интегрирование изображения
- Умножение изображений
- Умножение оригиналов
- Таблица оригиналов и изображений
- Обратное преобразование Лапласа
- Формула Римана-Меллина
- Операционный метод решения линейных дифференциальных уравнений и их систем
- VMath
- Инструменты сайта
- Основное
- Навигация
- Информация
- Действия
- Содержание
- Применения операционного исчисления
- Решение задачи Коши для ОДУ с постоянными коэффициентами
- Решение задачи Коши для систем линейных ДУ
- Решение ОДУ с помощью интеграла Дюамеля
- Решение задачи Коши с правой частью, содержащей функцию Хэвисайда
- Решение задачи Коши с периодической правой частью
- 💡 Видео
Видео:18+ Математика без Ху!ни. Дифференциальные уравнения. Однородное уравнение.Скачать

Преобразование Лапласа
Оригиналы и их изображения:
Основными первоначальными понятиями операционного исчисления являются понятия функции-оригинала и функции-изображения.
Пусть f(t) — действительная функция действительного переменного t (под t будем понимать время или координату).
Функция f(t) называется оригиналом, если она удовлетворяет следующим условиям:
- f(t)— кусочно-непрерывная при
т. е. она непрерывна или имеет точки разрыва I рода, причем на каждом конечном промежутке оси t таких точек лишь конечное число.
- Существуют такие числа
что для всех t выполняется неравенство
, т. е. при возрастании t функция f(t) может возрастать не быстрее некоторой показательной функции. Число
называется показателем роста f(t).
Условия 1-3 выполняются для большинства функций, описывающих различные физические процессы.
Первое условие означает, что процесс начинается с некоторого момента времени; удобнее считать, что в момент t = 0. Третьему условию удовлетворяют ограниченные функции (для них можно положить 
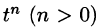
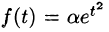
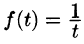
Замечание:
Функция f(t) может быть и комплексной функцией действительно переменного, т. е. иметь вид 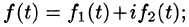
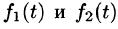
Изображением оригинала f(t) называется функция F(p) комплексного переменного 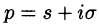
Операцию перехода от оригинала f(t) к изображению F(p) называют преобразованием Лапласа. Соответствие между оригиналом f(t) и изображением F(p) записывается в виде 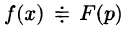
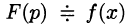
Теорема:
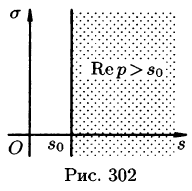
Существование изображения. Для всякого оригинала f(t) изображение F(p) существует (определено) в полуплоскости 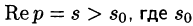
Докажем первую часть теоремы. Пусть 
Учитывая, что 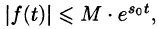
Отсюда вытекает абсолютная сходимость интеграла (78.1), т. е. изображение F(p) существует и однозначно в полуплоскости
Следствие:
Необходимый признак существования изображения. Если функция F(p) является изображением функции f(t) , то
Это утверждение непосредственно вытекает из неравенства (78.2), когда
Так как F(p) — аналитическая функция в полуплоскости
по любому направлению. Отсюда, в частности, следует, что функции 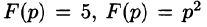
Отметим, что из аналитичности функции F(p) следует, что все ее особые точки должны лежать левее прямой 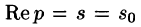
Теорема:
О единственности оригинала. Если функция F(p) служит изображением двух оригиналов 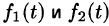
(Примем без доказательства.)
Пример:
Найти изображение единичной функции Хевисайда
Решение:
По формуле (78.1) при 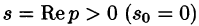
т. e. 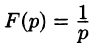
В дальнейшем функцию-оригинал будем кратко записывать в виде f(t) , подразумевал, что
Пример:
Найти изображение функции 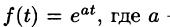
Решение:
Данная функция является оригиналом. По формуле (78.1) имеем
если Re(p — a) > 0. Таким образом,
Пример:
Найти изображение функции f(t) = t.
Решение:
В этом случае преобразование Лапласа имеет вид
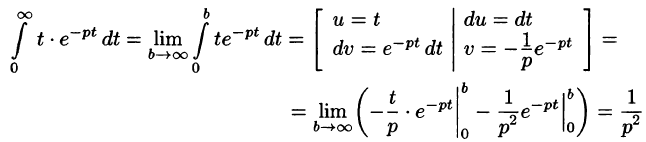
Замечание:
Функция 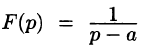
Свойства преобразования Лапласа
Находить изображения, пользуясь только определением изображения, не всегда просто и удобно. Свойства преобразования Лапласа существенно облегчают задачу нахождения изображений для большого числа разнообразных функций, а также задачу отыскания оригиналов по их изображениям.
Линейность
Линейной комбинации оригиналов соответствует такая же линейная комбинация изображений, т. е. если
— постоянные числа, то
Используя свойства интеграла, находим
Пример:
Найти изображения функций 
Решение:
Пользуясь свойством линейности, формулой (78.3), находим:
Аналогично получаем формулу
Далее, 
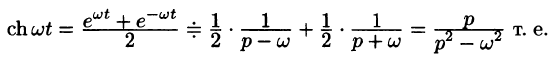
Аналогично получаем формулу
т.е. умножение аргумента оригинала на положительное число 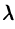
По формуле (78.1) имеем
(так как безразлично, какой буквой обозначена переменная интегрирования).
Например, пусть 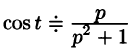
Смещение (затухание)
т. е. умножение оригинала на функцию 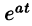
В силу формулы (78.1) имеем
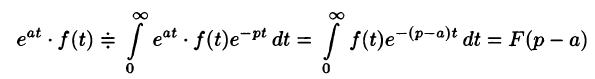
Благодаря этому свойству можно расширить таблицу соответствия между оригиналами и их изображениями:
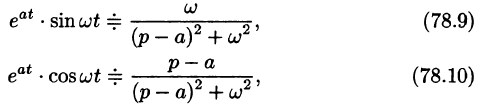
Пример:
Найти оригинал по его изображению
Решение:
Преобразуем данную дробь так, чтобы можно было воспользоваться свойством смещения:
(См. формулы (78.9), (78.10) и свойство линейности.)
Запаздывание
т. е. запаздывание оригинала на положительную величину 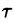
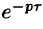
Положив 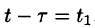
Поясним термин «запаздывание». Графики функции f(t) и 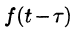
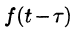
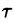
Рис. 304
Рис. 305
вправо (см. рис. 304). Следовательно, функции f(t) и 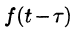
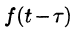
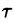
Свойство запаздывания удобно применять при отыскании изображения функций, которые на разных участках задаются различными аналитическими выражениями; функций, описывающих импульсные процессы.
называется обобщенной единично ной функцией (см. рис 305).
можно записать так:
Пример:
Найти изображение f(t) = t — 1.
Решение:
Для того чтобы быть оригиналом, функция f(t) должна удовлетворять условиям 1-3 (см. п. 78.1). В этом смысле исходную задачу можно понимать двояко.
Если понимать функцию f(t) как
т. е. 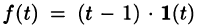
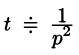
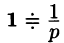
Если же понимать функцию f(t) как
т. е. 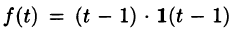
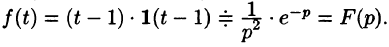
Пример:
Найти изображение функции
Решение:
Данная функция описывает единичный импульс (см. рис. 307), который можно рассматривать как разность двух оригиналов: единичной функции 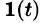
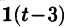
Пример:
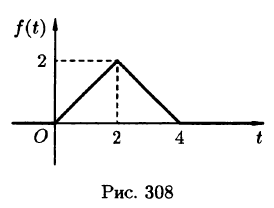
Найти изображение функции

Решение:
Функция-оригинал изображена на рис. 308. Запишем ее одним аналитическим выражением, используя функции Хевисайда 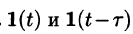
Раскроем скобки и приведем подобные слагаемые:
Изображение функции f(t) будет равно
Замечания:
1.Изображение периодического оригинала с периодом, равным Т,
есть
применяется значительно реже.
Дифференцирование оригинала
Если 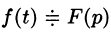
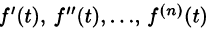
По определению изображения находим
Итак, 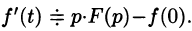
Аналогично найдем изображение третьей производной f»‘(t):
Применяя формулу (78.11) (п — 1) раз, получим формулу (78.14).
Замечание. Формулы (78.11)-(78.14) просто выглядят при нулевых начальных условиях: если
т. е. дифференцированию оригинала соответствует умножение его изображения на р.
Рассмотренное свойство дифференцирования оригинала вместе со свойством линейности широко используется при решении линейных дифференциальных уравнений.
Пример:
Найти изображение выражения
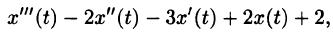
Решение:
Пусть 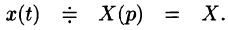
Дифференцирование изображения
Если 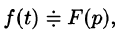
т. е. дифференцированию изображения соответствует умножение его оригинала на (-t).
Согласно теореме 78.1 существования изображения, F(p) является аналитической функцией в полуплоскости 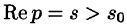
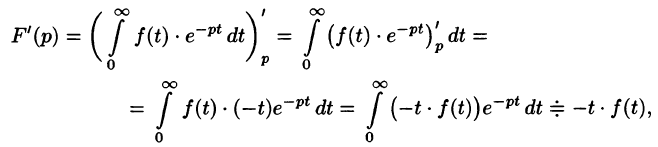
Пример:
Найти изображения функций
Решение:
Так как 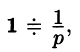
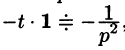
Продолжая дифференцирование, получим
С учетом свойства смещения получаем
Согласно формуле (78.5), 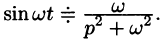
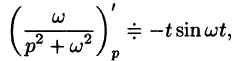
Аналогично, используя формулы (78.6), (78.7) и (78.8), находим
С учетом свойства смещения и формул (78.15) и (78.16), получаем
Интегрирование оригинала
т. е. интегрированию оригинала от 0 до t соответствует деление его изображения на р.
Функция 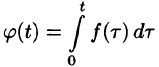
Пусть 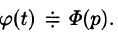
(так как 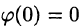
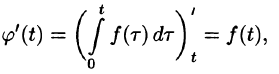
Интегрирование изображения
Если 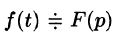
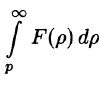
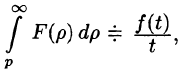
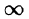
Используя формулу (78.1) и изменяя порядок интегрирования (обоснование законности этой операции опускаем), получаем
Пример:
Найти изображение функции 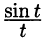
Решение:
т. е. 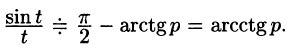
Умножение изображений
Если 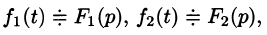
Можно показать, что функция 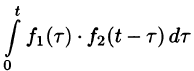
Используя преобразование Лапласа (78.1), можно записать
Область D интегрирования полученного двукратного интеграла определяется условиями 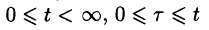
Изменяя порядок интегрирования и полагая 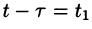
Интеграл в правой части формулы (78.17) называется сверткой функции 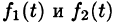
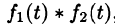
Можно убедиться (положив 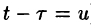
Умножение изображений соответствует свертыванию их оригиналов, т. е.
Пример:
Найти оригинал функций
Решение:
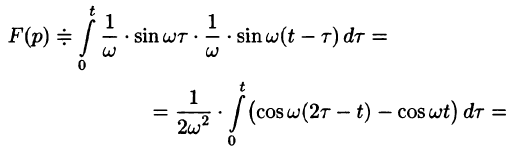
Следствие:
Если 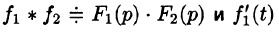
Запишем произведение 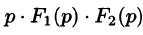
Первое слагаемое в правой части есть произведение изображений, соответствующих оригиналам 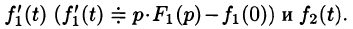
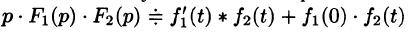
Формула (78.18) называется формулой Дюамеля. На основании свойства переместительности свертки формулу Дюамеля можно записать в виде
Формулу Дюамеля можно применять для определения оригиналов по известным изображениям.
Пример:
Найти оригинал, соответствующий изображению
Решение:
то на основании формулы Дюамеля (78.18) имеем
Умножение оригиналов
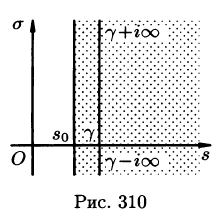
где путь интегрирования — вертикальная прямая 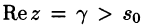
Рассмотренные свойства преобразования Лапласа представляют собой основные правила (аппарат) операционного исчисления. Для удобства пользования перечислим эти свойства.
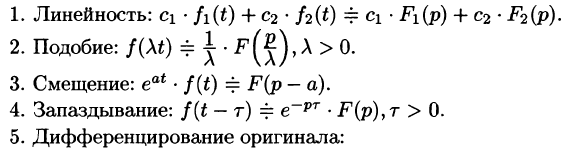
6. Дифференцирование изображения
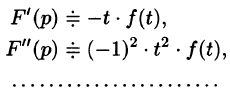
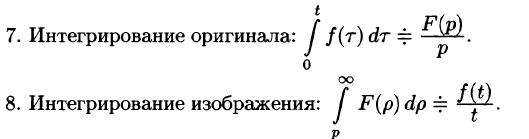
Таблица оригиналов и изображений
Составим краткую таблицу, устанавливающую соответствие между некоторыми оригиналами (часто встречающимися на практике) и их изображениями. Достаточно полная таблица оригиналов и изображений, позволяющая по заданному оригиналу находить изображение и наоборот, есть, в частности, в книге «Справочник по операционному исчислению» (авторы В. А. Диткин и П. И. Кузнецов).


Видео:Дифференциальное уравнение БесселяСкачать

Обратное преобразование Лапласа
Теоремы разложения:
Рассмотрим две теоремы, называемые теоремами разложения, позволяющие по заданному изображению F(p) находить соответствующий ему оригинал f(t).
Теорема:
Если функция F(p) в окрестности точки 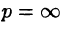
является оригиналом, имеющим изображение F(p), т. е.
Примем эту теорему без доказательства.
Пример:
Найти оригинал f(t), если
Решение:
Следовательно, на основании теоремы 79.1
Запишем лорановское разложение функции 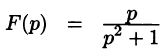
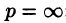
где 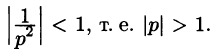
Теорема:
Если 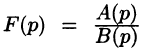
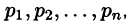
является оригиналом, имеющим изображение F(p).
Отметим, что дробь 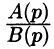
не может быть изображением.
Разложим правильную рациональную дробь 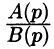
где 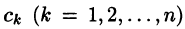
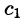
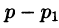
Переходя в этом равенстве к пределу при 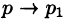
Итак, 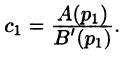
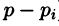
Подставляя найденные значения 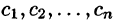
Так как по формуле (78.3)
то на основании свойства линейности имеем
Замечание:
Легко заметить, что коэффициенты 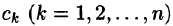
Можно показать, что если 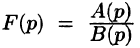
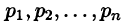
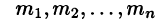
Теорему 79.2 можно сформулировать следующим образом:
Теорема:
Если изображение 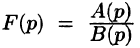
Формула Римана-Меллина
Общий способ определения оригинала по изображению дает обратное преобразование Лапласа (формула обращения Римана-Меллина), имеющее вид
где интеграл берется вдоль любой прямой 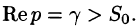
При определенных условиях интеграл (79.5) вычисляется по формуле
Замечание:
На практике отыскание функции-оригинала обычно проводят по следующему плану: прежде всего следует по таблице оригиналов и изображений попытаться отыскать для заданного изображения F(p) соответствующий ему оригинал; второй путь состоит в том, что функцию F(p) стараются представить в виде суммы простейших рациональных дробей, а затем, пользуясь свойством линейности, найти оригинал; наконец, использовать теоремы разложения, свойство умножения изображений, формулу обращения и т.д.
Пример:
Найти оригинал по его изображению
Решение:
Проще всего поступить так:
(использовали свойство линейности и формулы (78.5) и (78.6)).
Если же использовать теорему 79.2 разложения, то будем иметь:
корни знаменателя 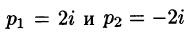
Пример:
Найти функцию-оригинал, если ее изображение
задано как
Решение:
— простой корень знаменателя, 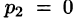
Приведем другой способ нахождения f(t). Разобьем дробь
на сумму простейших дробей:
Приведем третий способ нахождения f(t). Представим F(p) как
произведение 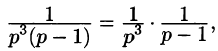
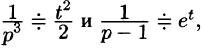
Операционный метод решения линейных дифференциальных уравнений и их систем
Пусть требуется найти частное решение линейного дифференциального уравнения с постоянными коэффициентами
удовлетворяющее начальным условиям
где 
Будем считать, что искомая функция y(t) вместе с ее рассматриваемыми производными и функция f(t) являются оригиналами.
Пусть 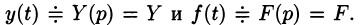
Полученное уравнение называют операторным (или уравнением в изображениях). Разрешим его относительно Y:
— алгебраические многочлены от p степени п и п-1 соответственно. Из последнего уравнения находим
Полученное равенство называют операторным решением дифференциального уравнения (80.1). Оно имеет более простой вид, если все начальные условия равны нулю, т. е.
В этом случае
Находя оригинал y(t), соответствующий найденному изображению (80.2), получаем, в силу теоремы единственности, частное решение дифференциального уравнения (80.1).
Замечание:
Полученное решение y(t) во многих случаях оказывается справедливым при всех значениях t (а не только при 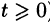
Пример:
Решить операционным методом дифференциальное уравнение 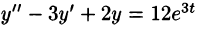
Решение:
Пусть 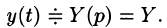
Подставляя эти выражения в дифференциальное уравнение, получаем операторное уравнение:
Отсюда 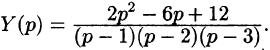
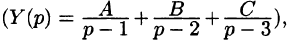
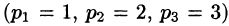
Пример:
Найти решение уравнения
при условии
Решение:
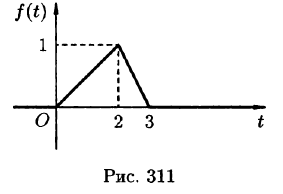
График данной функции имеет вид, изображенный на рисунке 311.
С помощью единичной функции правую часть данного дифференциального уравнения можно записать одним аналитическим выражением:
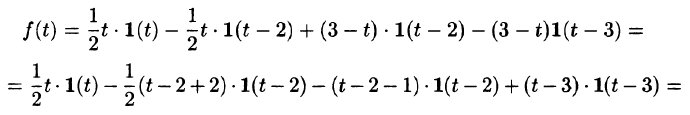
Таким образом, имеем
Операторное уравнение, при нулевых начальных условиях имеет вид
то по теореме запаздывания находим:
Аналогично применяется операционный метод для решения систем линейных дифференциальных уравнений с постоянными коэффициентами.
Покажем это на конкретном примере.
Пример:
Решить систему дифференциальных уравнений
Решение:
Система операторных уравнений принимает вид
Решая эту систему алгебраических уравнений, находим:
Переходя от изображений к оригиналам, получаем искомые решения:
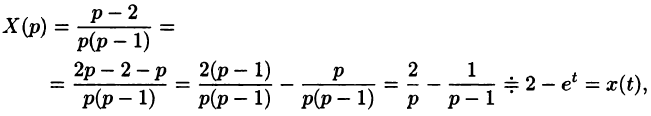
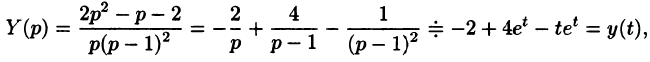
С помощью операционного исчисления можно также находить решения линейных дифференциальных уравнений с переменными коэффициентами, уравнений в частных производных, уравнений в конечных разностях (разностных уравнений); производить суммирование рядов; вычислять интегралы. При этом решение этих и других задач значительно упрощается.
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

VMath
Инструменты сайта
Основное
Навигация
Информация
Действия
Содержание
Видео:Геометрический смысл дифференциального уравненияСкачать

Применения операционного исчисления
Видео:Линейное неоднородное дифференциальное уравнение с постоянными коэффициентами 4y''-y=x^3-24x #1Скачать

Решение задачи Коши для ОДУ с постоянными коэффициентами
Пример 1.
Решить однородное дифференциальное уравнение с постоянными коэффициентами. begin &x»’+2x»+5x’=0,\ &x(0)=-1, ,, x'(0)=2, ,, x»(0)=0. end
Записываем изображения для левой и правой частей дифференциального уравнения. Для левой части используем теорему о дифференцировании оригинала: begin &x(t) risingdotseq X(p),\ &x'(t) risingdotseq pX(p)-x(0)=pX(p)+1,\ &x»(t) risingdotseq p^2X(p)-px(0)-x'(0)=p^2X(p)+p-2,\ &x»'(t) risingdotseq p^3X(p)-p^2x(0)-px'(0)-x»(0)=p^3X(p)+p^2-2p-0. end Справа стоит $0$, изображение для него тоже $0$.
Запишем уравнение с изображениями (операторное уравнение). Оно уже будет алгебраическим, а не дифференциальным: begin p^3X(p)+p^2-2p+2(p^2X(p)+p-2)+5(pX(p)+1)=0. end И найдем из него неизвестное $X(p)$: begin X(p)=-frac
. end Используя теоремы, приемы, таблицы операционного исчисления получим оригинал: begin X(p) risingdotseq x(t)=-displaystylefrac15-displaystylefrac45 e^mbox,2t+displaystylefrac35e^mbox,2t. end
Пример 2.
Решить неоднородное дифференциальное уравнение с постоянными коэффициентами. begin x»-2x’-3x=e^,\ x(0)=x'(0)=0. end
Записываем изображения для левой и правой частей дифференциального уравнения. Для левой части используем теорему о дифференцировании оригинала: begin &x(t) risingdotseq X(p),\ &x'(t) risingdotseq pX(p)-x(0)=pX(p),\ &x»(t) risingdotseq p^2X(p)-px(0)-x'(0)=p^2X(p), end Справа стоит $e^$, изображение равно $displaystylefrac$.
Запишем операторное уравнение: begin (p^2-2p-3)X(p)=frac. end Находим $X(p)$: begin X(p)=frac. end Используя, например, вторую теорему разложения, получим оригинал: begin X(p) risingdotseq displaystylefrac14,te^-displaystylefrac,e^+displaystylefrac,e^. end
Пример 3.
Решить неоднородное дифференциальное уравнение с постоянными коэффициентами. begin x»+3x’=mbox,2t,\ x(0)=2, ,, x'(0)=0. end
Пример 4.
Решить неоднородное дифференциальное уравнение с постоянными коэффициентами. begin x»+x’=e^t,\ x(1)=1, ,, x'(1)=2. end Так как начальные условия даны не при $t=0$, сразу применить теорему о дифференцировании оригинала мы не можем. Поставим вспомогательную задачу для функции $y(t)=x(t+1)$: begin y»+y’=e^,\ y(0)=1, ,, y'(0)=2. end Записываем операторное уравнение begin (p^2Y(p)-p-2)+(pY(p)-1)=displaystylefrac. end
Решаем полученное уравение: begin Y(p)=displaystylefrac+displaystylefrac
. end begin y(t)=displaystylefrac12e^+left(displaystylefrac-2right)e^+(3-e). end Со сдвигом на $1$ находим решение исходной задачи: begin x(t)=y(t-1)=displaystylefrac12e^+left(displaystylefrac-2right)e^+(3-e). end
Видео:13. Как решить дифференциальное уравнение первого порядка?Скачать

Решение задачи Коши для систем линейных ДУ
Пример 5.
Решить систему линейных дифференциальных уравнений с постоянными коэффициентами. begin left < begin&x’ = 2x+8, \ &y’ = x+4y+1, \ &x(0)=1,, y(0)=0. \ end right. end
Запишем изображения: begin begin x(t) risingdotseq X(p), & x'(t) risingdotseq p,X(p)-1, \ y(t) risingdotseq Y(p), & y'(t) risingdotseq p,Y(p). end end begin 8 risingdotseq displaystylefrac
, ,, 1 risingdotseq displaystylefrac
. end
Операторная система уравнений принимает вид: begin left < beginpX(p)-1 &= 2X(p)+displaystylefrac
, \ pY(p) &= X(p)+4Y(p)+displaystylefrac
.\ end right. end
Решаем систему, находим изображения $X(p)$, $Y(p)$ и их оригиналы $x(t)$, $y(t)$: begin X(p)=displaystylefrac
risingdotseq x(t)=-4+5e^. end begin Y(p)=displaystylefrac
risingdotseq y(t)=displaystylefrac34-displaystylefrac52,e^+displaystylefrac74,e^. end
Пример 6.
Решить систему линейных дифференциальных уравнений с постоянными коэффициентами. begin left < begin&x’ = 2x+8y, \ &y’ = x+4y+1, \ &x(0)=1,, y(0)=0.\ end right. end
begin begin x(t) risingdotseq X(p), & x'(t) risingdotseq p,X(p)-1, \ y(t) risingdotseq Y(p), & y'(t) risingdotseq p,Y(p),\ 1 risingdotseq displaystylefrac
. &\ end end
Операторная система уравнений принимает вид: begin left < beginpX(p)-1 &= 2X(p)+8Y(p), \ pY(p) &= X(p)+4Y(p)+displaystylefrac
.\ end right. end
Решаем систему находим изображения $X(p)$, $Y(p)$ и их оригиналы $x(t)$, $y(t)$: begin X(p)=displaystylefrac
risingdotseq x(t)=frac49-frac43,t+frac59,e^. end begin Y(p)=displaystylefrac
risingdotseq y(t)=-displaystylefrac+displaystylefrac13,t+displaystylefrac,e^. end
Пример 7.
Решить систему линейных дифференциальных уравнений с постоянными коэффициентами. begin left < begin&x’-2x-4y = mbox, t, \ &y’+x+2y = mbox,t, \ &x(0)=0,, y(0)=0.\ end right. end
Операторная система уравнений принимает вид: begin left < begin(p-2)X(p)-4Y(p) &= frac
, \ X(p)+(p+2)Y(p) &= frac
.\ end right. end
Решаем систему находим изображения $X(p)$, $Y(p)$ и их оригиналы $x(t)$, $y(t)$: begin X(p)=displaystylefrac
+displaystylefrac
-displaystylefrac
risingdotseq x(t)=2+4t-2,mbox,t-3,mbox,t. end begin Y(p)=-displaystylefrac
+displaystylefrac
risingdotseq y(t)=-2t+2,mbox,t. end
Видео:Дифференциальные уравнения. 11 класс.Скачать

Решение ОДУ с помощью интеграла Дюамеля
Введем обозначения:
Уравнение: $x^(t)+a_1,x^(t)+ldots+a_n,x(t)=f(t)$.
Начальные условия: $x(0)=x'(0)=ldots=x^=0$.
Неизвестная функция $x(t)$, имеющая изображение $X(p)$.
Сложная функция в правой части $f(t)$, имеющая изображение $F(p)$.
Запишем алгоритм решения.
1. Решается вспомогательное уравнение $$ y^(t)+a_1,y^(t)+ldots+a_n,y(t)=1.$$ С учетом начальных условий левая и правые части уравнений будут иметь изображения: begin begin y(t) & risingdotseq Y(p),\ y'(t) & risingdotseq p,Y(p),\ y»(t)& risingdotseq p^2Y(p),\ &cdots\ y^(t)& risingdotseq p^nY(p). end end Вспомогательное операторное уравнение запишем в виде: begin Y(p)cdot h(p) = frac
,\ h(p)=p^n+a_1p^+ldots+a_n. end $$Y(p) risingdotseq y(t).$$
2. Решается исходное уравнение. Левая часть уравнения совпадает с левой частью вспомогательного, поэтому операторное уравнение записывается так: $$ X(p)cdot h(p) = F(p),$$ при этом $h(p)$, используя решение вспомогательного уравнения, можно записать в виде begin h(p)=frac. end Тогда $$ X(p) = F(p),pY(p).$$ Для нахождения $x(t)$ необходимо найти оригинал для $pY(p)F(p)$, то есть вычислить интеграл из формулы Дюамеля: $$ p F(p) Y(p) risingdotseq y(0)cdot f(t)+intlimits_0^t f(tau),y'(t-tau),dtau,$$ где $y(t)$ — уже найденное решение вспомогательного уравнения.
Пример 8.
Решить задачу Коши с помощью интеграла Дюамеля. begin x»+2x’=frac<1+e^>, ,, x(0)=0, ,, x'(0)=0. end Решаем через интеграл Дюамеля в два этапа, как было описано выше.
2. Исходное уравнение в операторном виде: begin (p^2+2p)X(p)=F(p). end Правая часть этого уравнения такая же, как и для вспомогательного. Левую часть $frac<1+e^>$ обозначим $f(t)$, ее изображение $F(p)$. Тогда begin X(p)=frac
. end Решая вспомогательное уравнение, мы находили: begin (p^2+2p)Y(p)=frac
,, Rightarrow ,, p^2+2p=frac. end Тогда begin X(p)=frac<frac>=pF(p)Y(p). end
Теперь по формуле Дюамеля получаем: begin X(p)=p F(p) Y(p) risingdotseq x(t)=y(0)cdot f(t)+intlimits_0^t f(tau),y'(t-tau),dtau, end где $y(t)$ — уже найденное решение вспомогательного уравнения: begin begin & y(t)=-frac14+frac12t+frac14 e^,\ & y(0)=0,\ & y'(t-tau)=frac12-frac12e^. end end
Видео:Однородное дифференциальное уравнениеСкачать

Решение задачи Коши с правой частью, содержащей функцию Хэвисайда
Пример 9
Решить задачу Коши, когда правая часть дифференциального уравнения содержит составную функцию (выражаемую через функцию Хэвисайда). begin left < begin&x»+x=eta(t)-eta(t-2), \ &x(0)=0,\ &x'(0)=0. end right. end
Запишем изображения для левой и правой частей уравнения: begin &x»+x risingdotseq p^2,X(p)+X(p),\ &eta(t)-eta(t-2) risingdotseq frac
-frac<e^>
. end Для правой части, содержащей функцию Хэвисайда, воспользовались теоремой запаздывания.
Находим изображение для $displaystylefrac
$ с помощью теоремы об интегрировании оригинала: begin &frac
risingdotseq mbox,t ,, Rightarrow\ &frac
risingdotseq intlimits_0^t,mbox,tau,dtau=-mbox,t+1. end Тогда изображение для $displaystylefrac<e^>
$ по теореме запаздывания будет равно: begin frac<e^>
risingdotseq (-mbox,(t-2)+1)eta(t-2). end
Решение заданного уравнения: begin x(t)= (1-mbox,t)eta(t)-(1-mbox,(t-2))eta(t-2). end
Пример 10
Решить задачу Коши, когда правая часть дифференциального уравнения задана графически (и выражается через функцию Хэвисайда). begin left < begin&x»+4x=f(t). \ &x(0)=0,\ &x'(0)=0. end right. end
Запишем аналитическое выражение для $f(t)$ с помощью функции Хэвисайда и найдем ее изображение: begin &f(t)=2teta(t)-4(t-1)eta(t-1)+2(t-2)eta(t-2),\ &F(p)=frac
(1-2e^+e^). end Операторное уравнение имеет вид: begin &X(p)(p^2+4)=frac
(1-2e^+e^),, Rightarrow\ &X(p)=frac
(1-2e^+e^). end
Для первого слагаемого найдем оригинал, разложив дробь на сумму простейших: begin frac
=frac-frac risingdotseq frac12t-frac14,mbox,2t. end Для остальных слагаемых воспользуемся теоремой запаздывания: begin X(p)risingdotseq x(t)= frac12left(t-frac12,mbox,2tright)eta(t)-\ -left((t-1)-frac12,mbox,2(t-1)right)eta(t-1)+\ +frac12left((t-2)-frac12,mbox,2(t-2)right)eta(t-2). end
Видео:Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Решение задачи Коши с периодической правой частью
Периодическую правую часть тоже очень удобно записывать с помощью функции Хэвисайда.
Пусть $f(t)$ — периодическая с периодом $T$ функция-оригинал. Обозначим через $f_0(t)$ функцию: begin f_0(t)=begin f(t),& 0 oplaplace/seminar5_2.txt · Последние изменения: 2021/05/28 18:23 — nvr
💡 Видео
Дифференциальные уравнения, 2 урок, Дифференциальные уравнения с разделяющимися переменнымиСкачать

Составить дифференциальное уравнение семейства кривыхСкачать

Откуда появляются дифференциальные уравнения и как их решатьСкачать

14. Дифференциальные уравнения второго порядка, допускающие понижение порядкаСкачать

Дифференциальные уравнения, 1 урок, Дифференциальные уравнения. Основные понятияСкачать

1. Что такое дифференциальное уравнение?Скачать

Дифференциальные уравнения, 5 урок, Уравнение БернуллиСкачать

Дифференциальные уравнения, 3 урок, Однородные уравненияСкачать

Однородное линейное дифференциальное уравнение. Алгоритм решенияСкачать


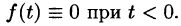
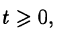 т. е. она непрерывна или имеет точки разрыва I рода, причем на каждом конечном промежутке оси t таких точек лишь конечное число.
т. е. она непрерывна или имеет точки разрыва I рода, причем на каждом конечном промежутке оси t таких точек лишь конечное число.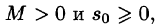 что для всех t выполняется неравенство
что для всех t выполняется неравенство 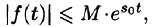 , т. е. при возрастании t функция f(t) может возрастать не быстрее некоторой показательной функции. Число
, т. е. при возрастании t функция f(t) может возрастать не быстрее некоторой показательной функции. Число 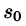 называется показателем роста f(t).
называется показателем роста f(t).