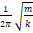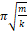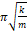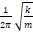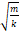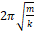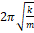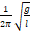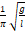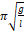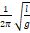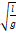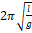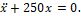Дифференциальное уравнение колебательного движения груза подвешенного к пружине имеет вид х 20х 0

Глава 13. Динамика точки.

13.4. Свободные незатухающие колебания.

13.4.1. Груз массой m = 25 кг подвешен к пружине с коэффициентом жесткости с = 800 Н/м и находится в свободном прямолинейном вертикальном колебательном движении. Определить модуль ускоре­ния груза в момент времени, когда центр тяжести груза находится на расстоянии 5 см от положения статического равновесия. (Ответ 1,6)

13.4.2. Груз массой m = 20 кг подвешен к пружине с коэффициентом жесткости с = 400 Н/м и находится в свободном прямолинейном вертикальном колебательном движении. Определить, на каком рас­стоянии от положения статического равновесия находится центр тяжести груза в момент времени, когда его ускорение равно 3 м/с. (Ответ 0,15)

13.4.3. Определить приведенный коэффициент жесткости в Н/см двух последовательно соединенных пружин с коэффициентами жесткости с₁ = 2 Н/см и с₂ = 18 Н/см. (Ответ 1,8)

13.4.4. Коэффициенты жесткости пружин с₁ = 2 Н/м, с₂ = 4 Н/м и с₃ = 6 Н/м. Определить коэффициент жесткости пружинной подвески. (Ответ 1,09)

13.4.5. Дифференциальное уравнение колебательного движения груза массой m = 0,5 кг, подвешенного к пружине, имеет вид у + 60у = 0. Определить коэффициент жесткости пружины. (Ответ 30)

13.4.6. Определить максимальное удлинение пру­жины АВ в см при свободных вертикальных колебаниях груза, если он прикреплен в точ­ке В к недеформированной пружине и отпус­кается из состояния покоя. Статическая де­формация пружины под действием груза равна 2 см.
(Ответ 4)

Видео:13. Как решить дифференциальное уравнение первого порядка?Скачать

13.4.7. Тело массой m = 10 кг подвешено к пружине и совершает свобод­ные вертикальные колебания с периодом Т = 0,8 с. Определить коэф­фициент жесткости пружины. (Ответ 617)

13.4.8. Материальная точка массой m = 5 кг под­вешена к пружине и находится в свободном вертикальном колебательном движении, закон которого задан графиком функции х = x(t). Определить коэффициент жесткости пружины. (Ответ 548)

13.4.9. Определить период свободных вертикальных колебаний груза массой m = 80 кг, который прикреплен к пружине с коэффициен­том жесткости с = 2 кН/м. (Ответ 1,26)

13.4.10. Определить период свободных вертикальных колебаний тела, подвешенного к пружине, если статическая деформация пружины λ = 20 см. (Ответ 0,897)

13.4.11. Тело подвешено к пружине и совершает свободные вертикаль­ные колебания с периодом Т = 0,5 с. Определить массу точки, если коэффициент жесткости пружины с = 200 Н/м (Ответ 1,27)

13.4.12. Тело, подвешенное к пружине, совершает свободные вертикальные колебания, заданные графиком функции у = у(t). Определить мас­су тела, если коэффициент жесткости пружины с = 300 H/м. (Ответ 122)

13.4.13. Период свободных вертикальных колебаний груза, подвешенного на пружине с коэффициентом жесткости с = 2 кН/м, равен Т = πс. Оп­ределить массу груза. (Ответ 500)

13.4.14. Дифференциальное уравнение колебательного движения груза, подвешенного к пружине, имеет вид х + 20х = 0. Определить массу груза, если коэффициент жесткости пружины с = 150 Н/м. (Ответ 7,5)

Дифференциальное уравнение колебательного движения груза подвешенного к пружине имеет вид х 20х 0

Тестовые вопросы по теме «Прямолинейные колебания точки»

Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

— Как называется число полных колебаний, совершаемых за 1 с ?

1. частота колебаний

2. период колебаний

3. фаза колебаний

4. циклическая колебаний

5. амплитуда колебаний

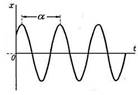
— На рисунке представлен график колебаний. (для справки k — циклическая частота собственных колебаний; b — коэффициент вязкого сопротивления; f — коэффициент сухого трения; p — частота вынуждающей силы)

1. вынужденных при b =0, f =0, p k

2. затухающих при b k , f =0, p =0,

3. затухающих при b > k , f =0, p =0,

Видео:Колебательное движение. Свободные колебания | Физика 9 класс #23 | ИнфоурокСкачать

4. свободных при b =0, f =0, p =0.

— На представленном рисунке величина обозначенная как « α » — это.

1. период свободных колебаний

2. полупериод свободных колебаний

3. полупериод вынужденных колебаний

4. период вынужденных колебаний

— Данное дифференциальное уравнение d 2 x d t 2 + k 2 x =0 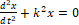является уравнением.

1. вынужденных колебаний без учета сил сопротивления (случай резонанса)

2. свободных колебаний без учета сил сопротивления

3. вынужденных колебаний без учета сил сопротивления

4. вынужденных колебаний с учетом сил сопротивления

Видео:Дифференциальные уравнения. 11 класс.Скачать

5. свободных колебаний с учетом сил сопротивления

— Период колебаний пружинного маятника определяется выражением?

1. 1 2 π m k

2. 2 π m k

3. 2 π k m

4. 1 2 π k m

5. m k

— Частота колебаний пружинного маятника определяется выражением?

1. 1 2 π m k

2. 2 π m k

3. 2 π k m

4. 1 2 π k m

5. m k

— Период колебаний математического мятника определяется выражением?

1. 1 2 π g l

2. 1 π g l

3. 2 π g l

4. 1 2 π l g

5. l g

— Частота колебаний математического маятника определяется выражением ?

1. 1 π g l

2. 2 π l g

3. 1 2 π l g

4. l g

— Дифференциальное уравнение колебательного движения материальной точки дано в виде x 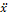+ 10 х = 1,5sin(5 t + 0,4). Если максимальное значение вынуждающей силы равно 60 Н, то масса точки равна…

— На тело, которое подвешено к пружине, действует вертикальная вынуждающая сила F = 30sin20 t. Если угловая частота собственных колебаний тела равна 25 рад/с, то коэффициент динамичности равен…

— Дифференциальное уравнение колебательного движения материальной точки имеет вид x 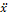+ 36 х = 50sin(5 t + 0,8). Тогда коэффициент динамичности равен…

— На тело массой 3 кг , которое подвешен к пружине, действует вертикальная вынуждающая сила F = 10sin5 t. Если коэффициент динамичности равен 4, то коэффициент жесткости пружины равен…

— На тело массой 50 кг , которое подвешен к пружине, действует вертикальная вынуждающая сила F = 200sin10 t. Если амплитуда вынужденных колебаний равна 0,04 м, то коэффициент жесткости пружины в кН/м равен…

— Дифференциальное уравнение вертикального колебательного движения материальной точки на пружине дано в виде x 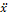+ 16 х = 20sin(6 t + 0,7). Если максимальное значение вынуждающей силы равно 80 Н, то коэффициент жесткости пружины равен…

— Дифференциальное уравнение колебательного движения материальной точки дано в виде 5 x 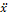+ 320 х = 90sin7 t. Тогда угловая частота собственных колебаний точки равна…

— Статическая деформация пружины, к которой подвешен груз, равна λ = 2 см. Ускорение земного притяжения принять равным 10 м/с 2 . Тогда колебательное движеиие груза описывается дифференциальным уравнением.

1. x +400 x =0 ;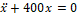

2. x +200 x =0 ;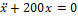

3. x +450 x =0 ;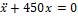

4. x +500 x =0 ;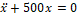

5. x +250 x =0.

— Материальная точка массой 0,6 кг колеблется на вертикальной пружине согласно закону х = 25 + 3sin20 t (см). Тогда в момент времени 2 с модуль реакции пружины равен…

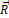
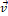
— Материальная точка массой 1 кг колеблется на вертикальной пружине в густой смазке с силой сопротивления R = — 0,1 v . В момент времени, когда ускорение точки равно 14 м/с 2 и скорость точки равна 2 м/с, то реакция пружины равна…

Видео:Дифференциальное уравнение от Бермана ★ Решите дифференциальное уравнение 2-го порядка ★ xy''=y'Скачать

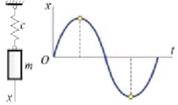
— Груз, подвешенный к пружине, совершает свободные колебания, график которых изображен на рисунке. Начало оси x совпадает с положением центра масс груза при равновесии системы. Начальные условия движения имеют вид.

1. x 0 = x 0 >0, x 0 = V 0 =0 ;

2. x 0 =0, x 0 = V 0 >0 ;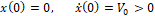

3. x 0 = x 0 x 0 = V 0 =0 ;

4. x 0 =0, x 0 = V 0 ;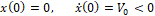

5. x 0 = x 0 >0, x 0 = V 0 >0 .

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

📽️ Видео

2. Дифференциальные уравнения с разделяющимися переменными. Часть 1.Скачать

1. Что такое дифференциальное уравнение?Скачать

Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Линейное дифференциальное уравнение первого порядка (1-x^2)*y'-xy=1Скачать

Решение физических задач с помощью дифференциальных уравненийСкачать

Дифференциальные уравнения, 2 урок, Дифференциальные уравнения с разделяющимися переменнымиСкачать

Линейное неоднородное дифференциальное уравнение 2 способаСкачать

Решение дифференциальных уравнений. Практическая часть. 11 класс.Скачать

Составить дифференциальные уравнения семейств линийСкачать

4. Однородные дифференциальные уравнения (часть 1)Скачать

7. Линейные дифференциальные уравнения первого порядка. Метод Бернулли.Скачать

Дифференциальные уравнения движения точкиСкачать

18+ Математика без Ху!ни. Дифференциальные уравнения. Однородное уравнение.Скачать