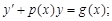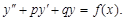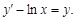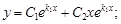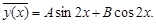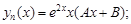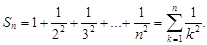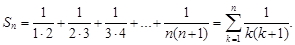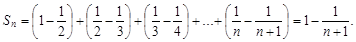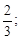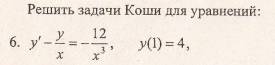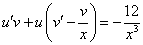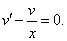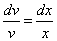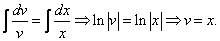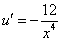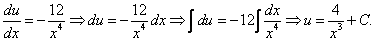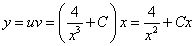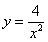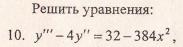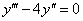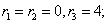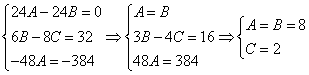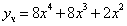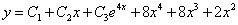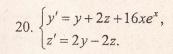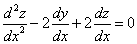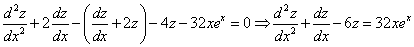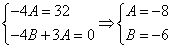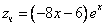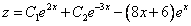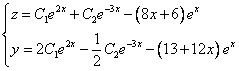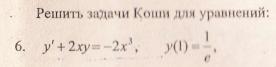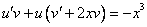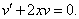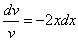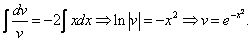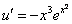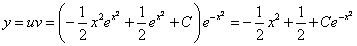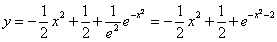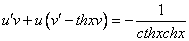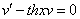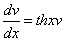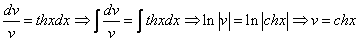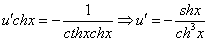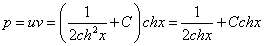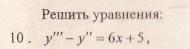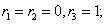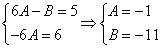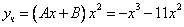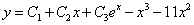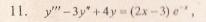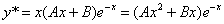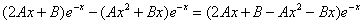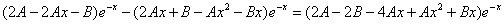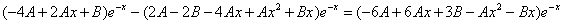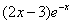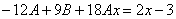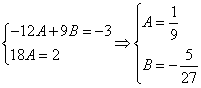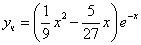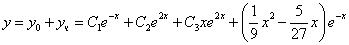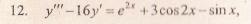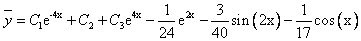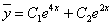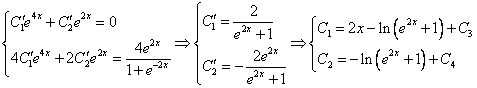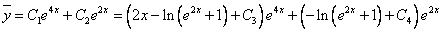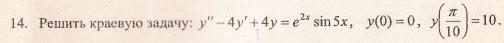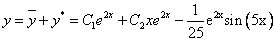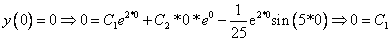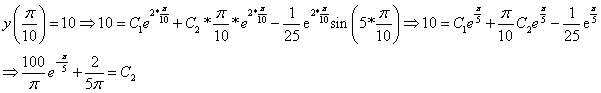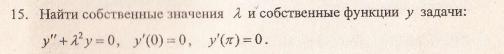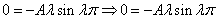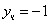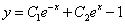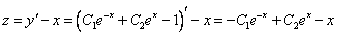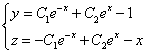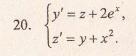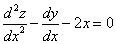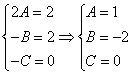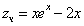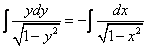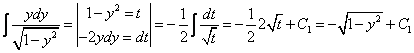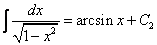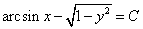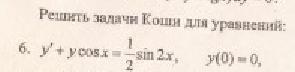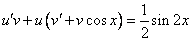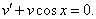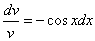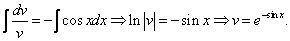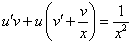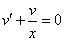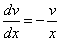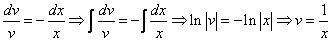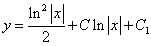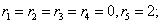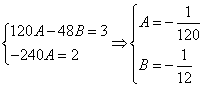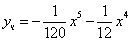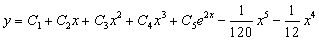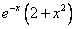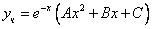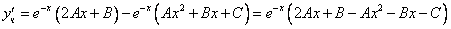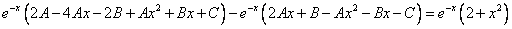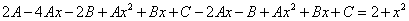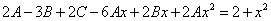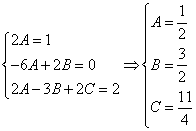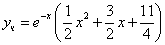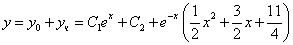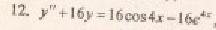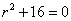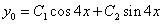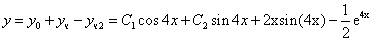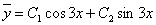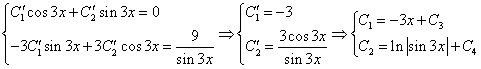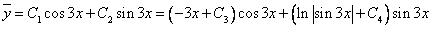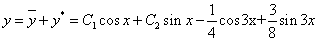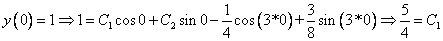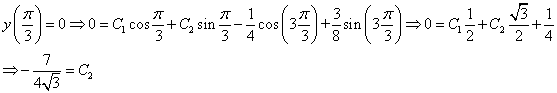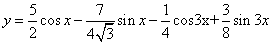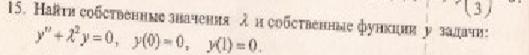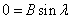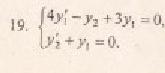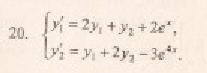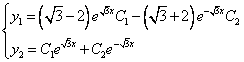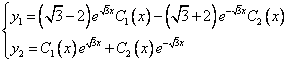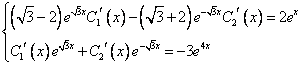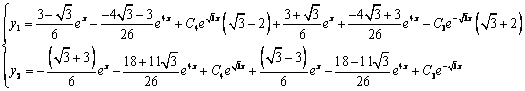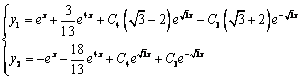Линейное дифференциальное уравнение (*) назовём уравнением с постоянными коэффициентами, если в этом уравнении коэффициенты постоянны, то есть ai(x)=const. Тогда соответствующее однородное уравнение L(y)=0 будет иметь вид 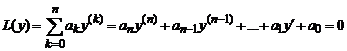
Решение уравнения (6) будем искать в виде y = e rx . Тогда y’ = r·e rx , y» = r 2 ·e rx ,…, y ( n ) = r n ·e rx . Подставляя в (6), получаем
Пример №1 . Для уравнения y»-3y’ + 2y=0 корни характеристического уравнения r 2 — 3r + 2 = 0 равны r1 = 1, r2 = 2 (корни были найдены через сервис нахождения дискриминанта). Следовательно, фундаментальную систему решений составляют функции y1 = e x , y2 = e 2 x , а общее решение записывается в виде y = C1e x + C2e 2 x .
2. Среди корней характеристического уравнения есть кратные. Предположим, что r1 имеет кратность α, а все остальные различны. Рассмотрим вначале случай r1 = 0. Тогда характеристическое уравнение имеет вид:
an(x)·r n +an-1(x)·r n-1 + . + an-α(x)·r α =0
так как в противном случае r не являлось бы корнем кратности α. Следовательно, дифференциальное уравнение имеет вид:
an(x)·y (n) +an-1(x)·y (n-1) + . + an-α(x)·y α =0
то есть не содержит производных порядка ниже α. Этому уравнению удовлетворяют все функции, у которых производные порядка α и выше равны нулю. В частности, таковыми являются все полиномы степени не выше α-1, например,
1, x, x 2 , …, x α-1 . (9)
Покажем, что данная система линейно независима. Составив определитель Вронского этой системы функций, получим
Пример №2 . Для уравнения y»’-4y»+4y’ = 0 характеристическое уравнение r 3 -4r 2 + 4r = 0 имеет корни r=0 кратности 1 и r=2 кратности 2, так как r 3 -4r 2 + 4r = r(r-2) 2 , поэтому фундаментальной системой решений исходного уравнения является система функций y1 = 1, y2 = e 2 x , y3 = xe 2 x , а общее решение имеет вид y = C1 + C2e 2 x + C3xe 2 x .
3. Среди корней характеристического уравнения есть комплексные корни. Можно рассматривать комплексные решения, но для уравнений с действительными коэффициентами это не очень удобно. Найдём действительные решения, соответствующие комплексным корням. Так как мы рассматриваем уравнение с действительными коэффициентами, то для каждого комплексного корня rj = a+bi кратности α характеристического уравнения комплексно сопряжённое ему число rk = a-bi также является корнем кратности α этого уравнения. Соответствующими этим корням парами решений являются функции yj l =x l ·e (a+b·i)x и yk l =x l ·e (a-b·i)x , l=0,1. α-1. Вместо этих решений рассмотрим их линейные комбинации
Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Дифференциальные уравнения второго порядка
1) Линейные однородные дифференциальные уравнения
второго порядка с постоянными коэффициентами
Линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами p и q называется уравнение вида

Алгебраическое уравнение k 2 + pk + q = 0 называется характеристическим уравнением для данного дифференциального уравнения, а его корни – характеристическими числами (корнями).
Для нахождения общего решения уравнения (8):
1. Запишем соответствующее характеристическое уравнение
2. В соответствии со знаком дискриминанта возможны три случая:
а) D > 0. Тогда характеристическое уравнение имеет два действительных корня k1 ¹ k2, и общее решение уравнения (8) имеет вид
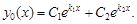
б) D = 0. Тогда k = k1 = k2 – действительный корень и общее решение уравнения (8) имеет вид
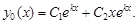
2)
3)
1. Запишем характеристическое уравнение k 2 + k – 2 = 0.
Найдем его корни

Так как k1 ¹ k2 – действительные числа, то общее решение находим по формуле (9)
2. Запишем характеристическое уравнение k 2 + 2k + 1 = 0.
Найдем его корни
В этом случае общее решение находим по формуле (10)
3. Запишем характеристическое уравнение k 2 + 4k + 5 = 0.
Найдем его корни

Общее решение находим по формуле (11)
Тест 19. Однородным дифференциальным уравнением второго порядка с постоянными коэффициентами является уравнение вида:
1)
2)
3)
4)
5)
Тест 20. Однородным дифференциальным уравнением второго порядка с постоянными коэффициентами является:
1)
2)
3)
4)
5)
Тест 21. При решении однородного дифференциального уравнения второго порядка с постоянными коэффициентами 
1) вводится подстановка вида y = u × v, где u = u(x) и v = v(x) – некоторые неизвестные функции;
2) вводится подстановка вида y = u × x, где u = u(x) – некоторая неизвестная функция;
3) составляется характеристическое уравнение k 2 + pk + q = 0.
Тест 22. Характеристическое уравнение k 2 + pk + q = 0 имеет два различных действительных корня k1 и k2. Тогда общее решение однородного дифференциального уравнения второго порядка с постоянными коэффициентами 
1)
2) y = u × x, где u = u(x) – некоторая неизвестная функция;
3)
4)
Тест 23. Характеристическое уравнение k 2 + pk + q = 0 имеет комплексные корни 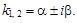
ференциального уравнения второго порядка с постоянными коэффициентами 
1)
2) y = u × x, где u = u(x) – некоторая неизвестная функция;
3)
4)
Тест 24. Характеристическое уравнение k 2 + pk + q = 0 имеет равные корни k1 = k2. Тогда общее решение однородного дифферен-
циального уравнения второго порядка с постоянными коэффициентами 
1)
2) y = u × x, где u = u(x) – некоторая неизвестная функция;
3)
4)
Тест 25. Характеристическое уравнение k 2 + pk + q = 0 имеет комплексные корни 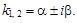
ференциального уравнения второго порядка с постоянными коэффициентами 
1)
2) y = u × x, где u = u(x) – некоторая неизвестная функция;
3)
4)
Тест 26. Характеристическое уравнение k 2 + pk + q = 0 имеет D = 0. Тогда общее решение однородного дифференциального уравнения второго порядка с постоянными коэффициентами 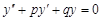
1)
2) y = u × x, где u = u(x) – некоторая неизвестная функция;
3)
4)
Тест 27. Характеристическое уравнение k 2 + pk + q = 0 имеет D 2 + Bx + C и т. д.
Пример 10. Определить вид частного решения уравнения
Запишем соответствующее однородное уравнение
1. Характеристическое уравнение k 2 – 4k + 3 = 0 имеет корни k1 = 1; k2 = 3.
2. В правой части данного уравнения функция вида (13)
3. Здесь a = 2 – не является корнем характеристического уравнения; 
Следовательно, частное решение данного неоднородного уравнения надо искать в виде (14), т. е. 
2. Пусть в правой части уравнения (12) функция
f(x) 
Тогда частное решение уравнения (12) будем искать в виде решений, приведенных в таблице 5.
| Если a ± bi не являются корнями соответствующего характеристического уравнения | Если a ± bi – корни характеристического уравнения |
 (18) (18) |  (19) (19) |
Пример 11. Определить вид частного решения уравнения
Запишем соответствующее однородное уравнение
1. Характеристическое уравнение k 2 + 4k – 2 = 0 имеет корни
2. В правой части данного уравнения функция вида (17)
f(x) 
3. Здесь a = 0; b = 2. Составленные из этих значений комплексные числа a ± bi = 0 ± 2i не являются корнями характеристического уравнения.
Следовательно, частное решение данного неоднородного уравнения надо искать в виде (18), т. е. 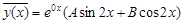
Тест 34. Характеристическое уравнение k 2 – 4k + 3 = 0, соответ-
ствующее однородному дифференциальному уравнению второго порядка с постоянными коэффициентами 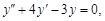

1)
2)
3)
4)
5)
Тест 35. Характеристическое уравнение k 2 – 4k + 4 = 0, соответ-
ствующее однородному дифференциальному уравнению второго порядка с постоянными коэффициентами 

1)
2)
3)
4)
5)
После того, как вид частного решения определен, методом неопределенных коэффициентов находим коэффициенты A и B.
Ответы на тестовые задания
| Номер теста |
| Правильный ответ |
Ряды
Числовые ряды
Пусть дана числовая последовательность 

называется числовым рядом, или просто рядом.
Числа 
Суммы конечного числа членов ряда 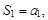

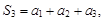


Пример 1. Пусть дана числовая последовательность

Тогда последовательность 
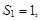

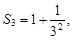
Последовательности (3) соответствует ряд

Пример 2.Рассмотрим ряд

Найдем его частичную сумму Sn. Имеем
Его частичную сумму можно упростить, если заметить, что
Тест 1. Определить второй член ряда
1)
2)
3)
4)
5)
Ряд (1) называется сходящимся, если последовательность его частичных сумм (2) сходится к какому-нибудь числу S, которое называется суммой ряда (1). Символически
Если же последовательность частичных сумм (2) расходится, то ряд (1) называется расходящимся. Такой ряд суммы не имеет.
Тест 2.Определить частичную сумму S3 ряда 1 + 


1)
2)
3)
4)
Простейшими примерами числовых рядов, вопрос о сходимости которых решен, являются следующие ряды:
1. 

Пример 3.Исследовать сходимость ряда 

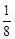

Это геометрический ряд, так как q = 
5) при
Видео:Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Дифференциальные уравнения (варианты)
Это уравнение вида 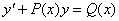


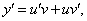
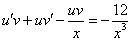
Так как одна из неизвестных функций может быть выбрана произвольно, возьмем в качестве v одно из частных решений уравнения
Тогда исходное дифференциальное уравнение примет вид
Рассмотрим каждое из получившихся уравнений. Первое уравнение – дифференциальное уравнение с разделяющимися переменными. Разделяем переменные:
Подставим найденную функцию v во второе уравнение 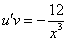
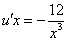
Это дифференциальное уравнение с разделяющимися переменными. Решая его, находим функцию и:
Возвращаясь к функции у, получим
Используем условие 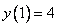

Ответ:
Решим соответствующее однородное уравнение
Составим характеристическое уравнение 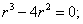
Так как его корни действительные и есть кратные, общее решение однородного уравнения имеет вид 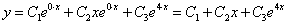
Частное решение неоднородного уравнения будем искать в виде 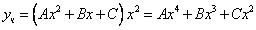
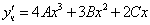
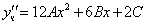
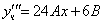
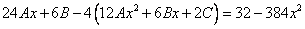
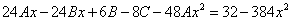
Тогда частное решение
Общее решение неоднородного примет вид:
Продифференцируем по х второе уравнение
Исключая с помощью первого уравнения 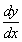
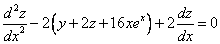
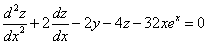
Таким образом, задача свелась к линейному неоднородному уравнению с постоянными коэффициентами второго порядка. Решим соответствующее однородное уравнение.
Характеристическое уравнение 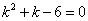
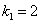
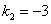
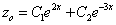
Частное решение неоднородного уравнения будем искать в виде 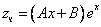

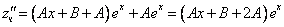
Подставим в исходное 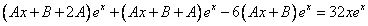
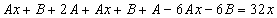
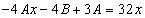
Тогда частное решение
Общее решение неоднородного примет вид:
Из второго уравнения
Ответ:
Видео:Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

Вариант 2
Данное уравнение – уравнение с разделяющимися переменными. Разделим переменные: 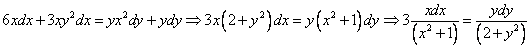
Посчитаем интегралы отдельно:
Тогда: 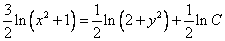
Ответ:
Это уравнение вида 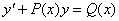


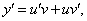
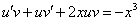
Так как одна из неизвестных функций может быть выбрана произвольно, возьмем в качестве v одно из частных решений уравнения
Тогда исходное дифференциальное уравнение примет вид
Рассмотрим каждое из получившихся уравнений. Первое уравнение – дифференциальное уравнение с разделяющимися переменными. Разделяем переменные:
Подставим найденную функцию v во второе уравнение 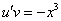
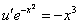
Это дифференциальное уравнение с разделяющимися переменными. Решая его, находим функцию и:
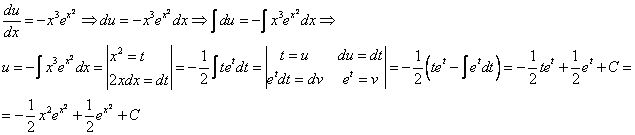
Используем условие 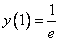
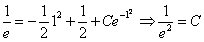
Ответ:
Данное уравнение не содержит у, следовательно понизить его порядок можно с помощью подстановки 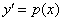
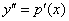
Отсюда 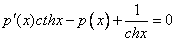
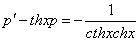
Замена 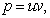
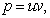
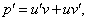
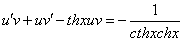
Так как одна из неизвестных функций может быть выбрана произвольно, возьмем в качестве v одно из частных решений уравнения
Тогда исходное дифференциальное уравнение примет вид
Рассмотрим каждое из получившихся уравнений. Первое уравнение – дифференциальное уравнение с разделяющимися переменными. Разделяем переменные:
Подставим найденную функцию v во второе уравнение 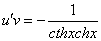
Это дифференциальное уравнение с разделяющимися переменными. Решая его, находим функцию и:
Возвращаясь к функции у, получим
Ответ:
Решим соответствующее однородное уравнение
Составим характеристическое уравнение 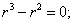
Так как его корни действительные и есть кратные, общее решение однородного уравнения имеет вид 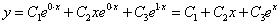
Частное решение неоднородного уравнения будем искать в виде 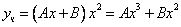

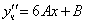
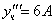
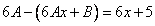
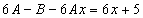
Тогда частное решение
Общее решение неоднородного примет вид:
Данное дифференциальное уравнение относится к линейным дифференциальным уравнениям с постоянными коэффициентами.
Решение уравнения будем искать в виде y = erx. Для этого составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами: r3-3r2+4= 0
Корни характеристического уравнения:
R1 = -1 и корень характеристического уравнения r2 = 2 кратности 2.
Следовательно, фундаментальную систему решений составляют функции: y1 = e-x, y2 = e2x, y3 = xe2x
Общее решение однородного уравнения имеет вид:
Рассмотрим правую часть: f(x) = (2•x-3)•e-x
Уравнение имеет частное решение вида:
Y’ =
Y» =
Y»’ =
которые подставляем в исходное дифференциальное уравнение:
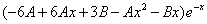
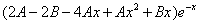
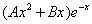
Приравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений:
Частное решение имеет вид:
Таким образом, общее решение дифференциального уравнения имеет вид:
Данное дифференциальное уравнение относится к линейным дифференциальным уравнениям с постоянными коэффициентами.
Решение уравнения будем искать в виде y = erx. Для этого составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами: r3 — 16r = 0
Корни характеристического уравнения:r1 = -4, r2 = 0, r3 = 4
Следовательно, фундаментальную систему решений составляют функции:
Y1 = e-4x, y2 = e0x, y3 = e4x
Общее решение однородного уравнения имеет вид:
Правая часть F(x) = e2•x+3cos2x-sinx
Будем искать отдельно частные решения для F1(x) = e2•x, F2(x) = 3cos2x, F3(x) = — sinx
Рассмотрим правую часть: F1(x) = e2•x
Линейное дифференциальное уравнение с постоянными коэффициентами и правой частью вида: R(x) = eαx(P(x)cos(βx) + Q(x)sin(βx)), где P(x), Q(x) — некоторые полиномы
Имеет частное решение y(x) = xkeαx(R(x)cos(βx) + S(x)sin(βx))
Где k — кратность корня α+βi характеристического полинома соответствующего однородного уравнения, R(x), S(x) — полиномы, подлежащие определению, степень которых равна максимальной степени полиномов P(x), Q(x).
Здесь P(x) = 1, Q(x) = 0, α = 2, β = 0.
Следовательно, число α + βi = 2 + 0i не является корнем характеристического уравнения.
Уравнение имеет частное решение вида:
Которые подставляем в исходное дифференциальное уравнение:
Y»’ -16y’ = (8•A•e2x) -16(2•A•e2x) = e2•x или -24•A•e2x = e2•x
Приравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений:
Решая ее, находим: A = -1/24;
Частное решение имеет вид: y* = -1/24e2x
Рассмотрим правую часть: F2(x) = 3•cos(2•x)
Поиск частного решения.
Уравнение имеет частное решение вида:y* = Acos(2x) + Bsin(2x)
Которые подставляем в исходное дифференциальное уравнение:
Y»’ -16y’ = (8•A•sin(2x)-8•B•cos(2x)) -16(2•B•cos(2x)-2•A•sin(2x)) = 3•cos(2•x)
или 40•A•sin(2x)-40•B•cos(2x) = 3•cos(2•x)
Приравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений:
Решая ее, находим: A = 0;B =-3/40;
Частное решение имеет вид:
Поиск частного решения.
Уравнение имеет частное решение вида: y* = Acos(x) + Bsin(x)
Которые подставляем в исходное дифференциальное уравнение:
Y»’ -16y’ = (A•sin(x)-B•cos(x)) -16(B•cos(x)-A•sin(x)) = — sin(x)
или 17•A•sin(x)-17•B•cos(x) = — sin(x)
Приравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений:
Решая ее, находим: A = -1/17;B = 0;
Частное решение имеет вид: y* = -1/17cos(x) + 0sin(x) или y* = -1/17cos(x)
Окончательно, общее решение данного уравнения
Данное дифференциальное уравнение относится к линейным дифференциальным уравнениям с постоянными коэффициентами.
Решение уравнения будем искать в виде y = erx. Для этого составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами: r2 -6 r + 8 = 0
Корни характеристического уравнения: r1 = 2, r2 = 4
Следовательно, фундаментальную систему решений составляют функции: y1 = e4x, y2 = e2x
Общее решение однородного уравнения имеет вид:
Для поиска частного решения воспользуемся методом вариации произвольных постоянных. Для этого решим систему:
Тогда окончательно
Данное дифференциальное уравнение относится к линейным дифференциальным уравнениям с постоянными коэффициентами.
Решение уравнения будем искать в виде y = erx. Для этого составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами: r2 -4 r + 4 = 0
Корни характеристического уравнения:
Корень характеристического уравнения r1 = 2 кратности 2.
Следовательно, фундаментальную систему решений составляют функции: y1 = e2x, y2 = xe2x
Общее решение однородного уравнения имеет вид:
Рассмотрим правую часть: f(x) = e2•x•sin(5•x)
Поиск частного решения.
Линейное дифференциальное уравнение с постоянными коэффициентами и правой частью вида: R(x) = eαx(P(x)cos(βx) + Q(x)sin(βx)), где P(x), Q(x) — некоторые полиномы
Имеет частное решение y(x) = xkeαx(R(x)cos(βx) + S(x)sin(βx))
Где k — кратность корня α+βi характеристического полинома соответствующего однородного уравнения, R(x), S(x) — полиномы, подлежащие определению, степень которых равна максимальной степени полиномов P(x), Q(x).
Здесь P(x) = 1, Q(x) = 0, α = 2, β = 5.
Следовательно, число α + βi = 2 + 5i не является корнем характеристического уравнения.
Уравнение имеет частное решение вида: y* = e2x(Acos(5x) + Bsin(5x))
Которые подставляем в исходное дифференциальное уравнение:
Y» -4y’ + 4y = (-e2x((20•A+21•B)•sin(5x)+(21•A-20•B)•cos(5x))) -4(e2x((2•B-5•A)•sin(5x)+(2•A+5•B)•cos(5x))) + 4(e2x(Acos(5x) + Bsin(5x))) = e2•x•sin(5•x)
или -25•A•e2x•cos(5x)-25•B•e2x•sin(5x) = e2•x•sin(5•x)
Приравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений:
Решая ее, находим: A = 0;B = -1/25;
Частное решение имеет вид: y* = e2x(0cos(5x) -1/25sin(5x)) илиy* =-1/25 e2x sin(5x)
Таким образом, общее решение дифференциального уравнения имеет вид:
Используем начальные условия
Тогда окончательно,
Характеристическое уравнение исходного дифференциального уравнения 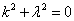
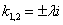
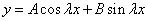
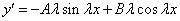
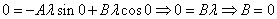
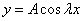
Подставляем во второе граничное условие
При А=0 и В=0 – тривиальное решение у=0
Поэтому 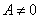
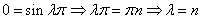
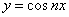
Метод исключения неизвестных.
Продифференцируем по х первое уравнение
Исключая с помощью второго уравнения 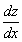
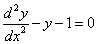
Таким образом, задача свелась к линейному неоднородному уравнению с постоянными коэффициентами второго порядка. Решим соответствующее однородное уравнение.
Характеристическое уравнение 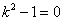
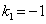
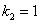
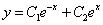
Частное решение неоднородного уравнения будем искать в виде 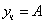
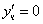
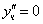
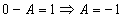
Тогда частное решение
Общее решение неоднородного примет вид:
Из первого уравнения
Ответ:
Продифференцируем по х второе уравнение
Исключая с помощью первого уравнения 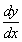
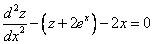
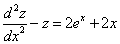
Таким образом, задача свелась к линейному неоднородному уравнению с постоянными коэффициентами второго порядка. Решим соответствующее однородное уравнение.
Характеристическое уравнение 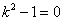
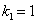
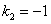
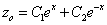
Частное решение неоднородного уравнения будем искать в виде 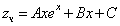
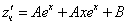
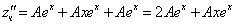
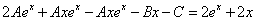
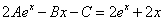
Тогда частное решение
Общее решение неоднородного примет вид:
Из второго уравнения
Ответ:
Видео:Видеоурок "Нахождение частных решений по виду правой части"Скачать

Вариант 5
Данное уравнение – уравнение с разделяющимися переменными. Разделим переменные: 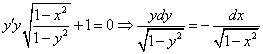
Посчитаем интегралы отдельно:
Тогда: 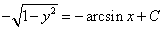
Ответ:
Это уравнение вида 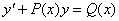


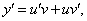
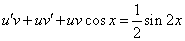
Так как одна из неизвестных функций может быть выбрана произвольно, возьмем в качестве v одно из частных решений уравнения
Тогда исходное дифференциальное уравнение примет вид
Рассмотрим каждое из получившихся уравнений. Первое уравнение – дифференциальное уравнение с разделяющимися переменными. Разделяем переменные:
Интегрируя, находим
Подставим найденную функцию v во второе уравнение 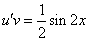
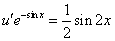
Это дифференциальное уравнение с разделяющимися переменными. Решая его, находим функцию и:
Возвращаясь к функции у, получим
Используем условие 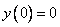
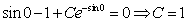
Ответ:
Данное уравнение не содержит у, следовательно понизить его порядок можно с помощью подстановки 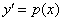
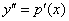
Отсюда 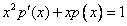
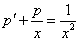
Замена 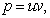
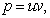
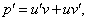
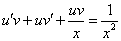
Так как одна из неизвестных функций может быть выбрана произвольно, возьмем в качестве v одно из частных решений уравнения
Тогда исходное дифференциальное уравнение примет вид
Рассмотрим каждое из получившихся уравнений. Первое уравнение – дифференциальное уравнение с разделяющимися переменными. Разделяем переменные:
Подставим найденную функцию v во второе уравнение 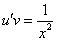
Это дифференциальное уравнение с разделяющимися переменными. Решая его, находим функцию и:
Возвращаясь к функции у, получим
Ответ:
Решим соответствующее однородное уравнение
Составим характеристическое уравнение 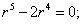
Так как его корни действительные и есть кратные, общее решение однородного уравнения имеет вид
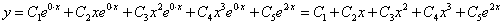
Частное решение неоднородного уравнения будем искать в виде 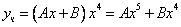
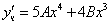
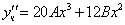
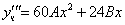
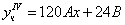
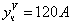
Подставим в исходное 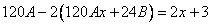
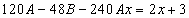
Тогда частное решение
Общее решение неоднородного примет вид:
Данное дифференциальное уравнение относится к линейным дифференциальным уравнениям с постоянными коэффициентами.
Решение уравнения будем искать в виде y = erx. Для этого составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами: r2 — r= 0
Вынесем r за скобку. Получим: r(r-1) = 0
Корни характеристического уравнения:r1 = 0, r2 = 1
Следовательно, фундаментальную систему решений составляют функции: y1 = e0x, y2 = ex.
Общее решение однородного уравнения имеет вид:
Рассмотрим правую часть: f(x) =
Уравнение имеет частное решение вида:
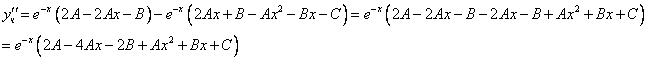
Приравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений:
Частное решение имеет вид:
Таким образом, общее решение дифференциального уравнения имеет вид:
Данное дифференциальное уравнение относится к линейным дифференциальным уравнениям с постоянными коэффициентами.
Составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами:
Корни характеристического уравнения:(комплексные корни): r1 = 4i, 
Общее решение однородного уравнения имеет вид:
Рассмотрим правую часть: f(x) = 16•cos(4•x)-16•e4x, будем искать отдельно частные решения для f1(x)= 16•cos(4•x) и для f2(x)= 16•e4x
Для f1(x) = 16•cos(4•x) имеем
Уравнение имеет частное решение вида: y ч1* = x (Acos(4x) + Bsin(4x))
Которые подставляем в исходное дифференциальное уравнение:
Приравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений:
Решая ее, находим: A = 0;B = 2;
Частное решение имеет вид: yч1* = x (0cos(4x) + 2sin(4x)) или y ч1* = 2xsin(4x)
Частное решение ищем в виде y(x) = xkeαx(R(x)cos(βx) + S(x)sin(βx))
Где k — кратность корня α+βi характеристического полинома соответствующего однородного уравнения, R(x), S(x) — полиномы, подлежащие определению, степень которых равна максимальной степени полиномов P(x), Q(x).
Здесь P(x) = 16, Q(x) = 0, α = 4, β = 0.
Следовательно, число α + βi = 4 + 0i не является корнем характеристического уравнения.
Уравнение имеет частное решение вида:
Которые подставляем в исходное дифференциальное уравнение:
Y» + 16y = (16•A•e4x) + 16(Ae4x) = 16•e4•x или 32•A•e4x = 16•e4•x
Приравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений:
Решая ее, находим: A = 1/2;
Частное решение имеет вид: y*ч2 = 1/2e4x
Таким образом, общее решение дифференциального уравнения имеет вид:
Данное дифференциальное уравнение относится к линейным дифференциальным уравнениям с постоянными коэффициентами.
Составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами: r2 + 9 = 0
Корни характеристического уравнения: r1 = -3i, r2 = 3i
Общее решение однородного уравнения имеет вид:
Для поиска частного решения воспользуемся методом вариации произвольных постоянных. Для этого решим систему:
Тогда окончательно
Данное дифференциальное уравнение относится к линейным дифференциальным уравнениям с постоянными коэффициентами.
Решение уравнения будем искать в виде y = erx. Для этого составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами: r2 + 1 = 0
Корни характеристического уравнения:(комплексные корни): r1 = i,
Следовательно, фундаментальную систему решений составляют функции:
Общее решение однородного уравнения имеет вид:
Рассмотрим правую часть: f(x) = 2•cos(3•x)-3•sin(3•x)
Поиск частного решения.
Линейное дифференциальное уравнение с постоянными коэффициентами и правой частью вида: R(x) = eαx(P(x)cos(βx) + Q(x)sin(βx)), где P(x), Q(x) — некоторые полиномы
Имеет частное решение y(x) = xkeαx(R(x)cos(βx) + S(x)sin(βx))
Где k — кратность корня α+βi характеристического полинома соответствующего однородного уравнения, R(x), S(x) — полиномы, подлежащие определению, степень которых равна максимальной степени полиномов P(x), Q(x).
Здесь P(x) = 2, Q(x) = -3, α = 0, β = 3.
Следовательно, число α + βi = 0 + 3i не является корнем характеристического уравнения.
Уравнение имеет частное решение вида: y* = Acos(3x) + Bsin(3x)
Которые подставляем в исходное дифференциальное уравнение:
Y» + y = (-9(A•cos(3x)+B•sin(3x))) + (Acos(3x) + Bsin(3x)) = 2•cos(3•x)-3•sin(3•x)
или -8•A•cos(3x)-8•B•sin(3x) = 2•cos(3•x)-3•sin(3•x)
Приравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений:
Решая ее, находим: A = -1/4;B = 3/8;
Частное решение имеет вид: y* = -1/4cos(3x) + 3/8sin(3x)
Таким образом, общее решение дифференциального уравнения имеет вид:
Используем начальные условия
Тогда окончательно,
Характеристическое уравнение исходного дифференциального уравнения 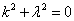
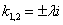
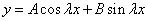
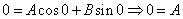
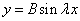
Подставляем во второе граничное условие
При А=0 и В=0 – тривиальное решение у=0
Поэтому 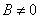
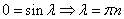
Продифференцируем по х второе уравнение
Исключая с помощью первого уравнения 
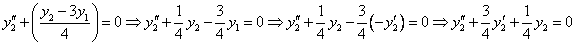
Таким образом, задача свелась к линейному однородному уравнению с постоянными коэффициентами второго порядка. Характеристическое уравнение 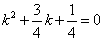
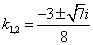
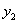
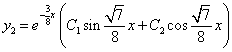
Из второго уравнения
Ответ:
Найдём сначала общее решение соответствующей однородной системы
Продифференцируем по х второе уравнение
Исключая с помощью первого уравнения 
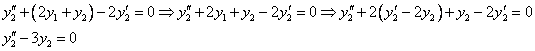
Таким образом, задача свелась к линейному однородному уравнению с постоянными коэффициентами второго порядка. Характеристическое уравнение 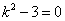
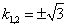
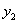
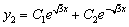
Из второго уравнения 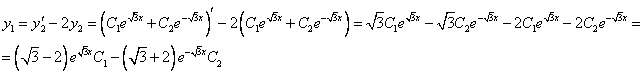
Принимаем частное решение первоначальной системы в виде:
Решаем данную систему по формулам Крамера, получим два дифференциальных уравнения первого порядка:
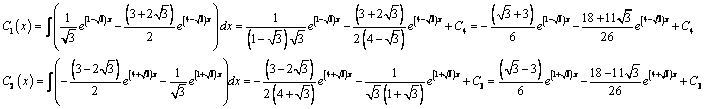
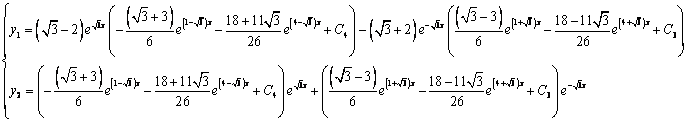
Ответ:
🔍 Видео
Линейное однородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами.Скачать

Линейное неоднородное дифференциальное уравнение с постоянными коэффициентами 4y''-y=x^3-24x #1Скачать

ЛОДУ 2 порядка c постоянными коэффициентамиСкачать

Характеристическое уравнение в ДУСкачать

Лукьяненко Д. В. - Дифференциальные уравнения - Лекция 1Скачать

16. Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентамиСкачать

Дифференциальные уравнения для самых маленькихСкачать

Линейные однородные дифференциальные уравнения n-го порядка с постоянными коэффициентамСкачать

Решение однородного дифференциального уравнения. Практическая часть. 11 класс.Скачать

Собственные значения и собственные векторы матрицы (4)Скачать

Дифференциальные уравнения с разделенными переменными. 11 класс.Скачать

Характеристическое уравнение диффураСкачать

Решение линейного однородного дифференциального уравнения. Практическая часть. 11 класс.Скачать

Дифференциальные уравнения, 8 урок, Линейные дифференциальные уравнения с const коэф-ами 2 порядкаСкачать

7. ДУ. ЛНДУ с правой частью спец вида (4270 Берман Г.Н)Скачать