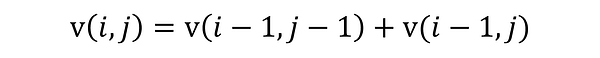Что нужно включить для решения рекурсивных уравнений (4 видео)

Использование табличного процессора MS Excel при решении задач на рекурсию Текст научной статьи по специальности « Математика»

Содержание

Аннотация научной статьи по математике, автор научной работы — Наталья Шамшина
Похожие темы научных работ по математике , автор научной работы — Наталья Шамшина
Using MS Excel spreadsheet to solve problems on recursion
Текст научной работы на тему «Использование табличного процессора MS Excel при решении задач на рекурсию»
Excel. Использование циклических ссылок для решения уравнений итерационным способом
7 комментариев для “Excel. Использование циклических ссылок для решения уравнений итерационным способом”
Продвинутый взгляд на рекурсию
🎬 Видео

Видео:Примеры рекурсивных алгоритмовСкачать

Аннотация научной статьи по математике, автор научной работы — Наталья Шамшина

Табличный процессор Excel целесообразно использовать для решения задач на рекурсию , чтобы освоить рекурсивный подход к решению математических и практических задач.

Видео:Рекурсивные функцииСкачать

Using MS Excel spreadsheet to solve problems on recursion

Excel spreadsheet useful for solving problems on recursion to learn a recursive approach to solving mathematical and practical problems.

Видео:Решение системы уравнений методом ГауссаСкачать

Текст научной работы на тему «Использование табличного процессора MS Excel при решении задач на рекурсию»

ФІЗИКО-МАТЕМАТИЧНА ОСВІТА (ФМО)

PHYSICAL AND MATHEMATICAL EDUCATION

Has been issued since 2013.

Видається з 2013.

Шамшина Н. Использование табличного процессора MS Excel при решении задач на рекурсию // Фізико-математична освіта. Науковий журнал. — Суми: СумДПУ ім.А.С.Макаренка, 2013. — № 1 (1). — С. 57-64.

Сумский государственный педагогический университет имени А.С. Макаренко,

ИСПОЛЬЗОВАНИЕ ТАБЛИЧНОГО ПРОЦЕССОРА MS EXCEL ПРИ РЕШЕНИИ ЗАДАЧ НА РЕКУРСИЮ

Рекурсия — это тонкий и изящный инструмент, который при умелом использовании способен сослужить добрую службу программисту. Одно из важных достоинств рекурсивных алгоритмов заключается в том, что они просты и наглядны. Изящество рекурсии в программировании можно сравнить только с изяществом метода индукции в математике. «Когда изучаются циклы — основа вычислительных процессов, без рекурсивных определений не обойтись. Циклы и рекурсия — близнецы-братья» [2]. С их помощью строятся лаконичные и легко понимаемые алгоритмы, а затем и соответствующие информационные модели в виде рекурсивных программ на том или ином языке программирования [4].

Обычно начинающий программист, впервые услышавший про рекурсию, впадает в легкое замешательство. Первоначальное знакомство с ней может вызвать непонимание и легкий шок. В общеобразовательной школе изучению рекурсии уделяют мало внимания. Тема трудна и для учеников, и для учителей. Умение описывать вычислительный процесс как циклический или рекурсивный дело далеко не простое.

Между тем, немало практических задач и большинство нетривиальных (олимпиадных) задач имеют рекурсивную природу. Следовательно, необходимо не только знакомить студентов различных специальностей и старших школьников с рекурсивными алгоритмами, но и уделять внимание поиску новых методик и технологий обучения, ориентированных на прочное усвоение соответствующих знаний.

Анализ современных методологических исследований 4 показывает, что преподаватели информатики педагогических вузов и популяризаторы информационных технологий в Интернете заинтересованно относятся к данному вопросу, хотя исследований теоретического и практического характера по теме очень мало.

ФІЗИКО-МАТЕМАТИЧНА ОСВІТА (ФМО)

Дидактические преимущества рекурсивного подхода, по сравнению с простым описанием функций и решением с его помощью соответствующих прикладных задач, положительно оценили коллеги Тульского государственного педагогического университета имени Л.Н. Толстого. Экспериментальная группа студентов показала лучшие результаты, по сравнению с контрольной группой, при решении задач через год после освоения курса «Финансовые функции». Сделан вывод о том, что рекурсивный подход «дает возможность не только всесторонне понять содержание излагаемого материала, но сделать это быстро и эффективно. И что особенно важно, полученные знания становятся достоянием долговременной памяти» [3]. Исследования проводились с использованием экономических задач, решения которых оформлялись в виде рекурсивных программ-функций на языке программирования вычислительной среды Mathcad.

Специализированные математические програмы, языки високого уровня, а вместе с ними и основи программирования студенты изучают на старших курсах сталкиваясь при этом с некоторыми трудностями, поскольку им приходится осваивать незнакомый язык программирования и одновременно логику программы. Можно ли студентов первых курсов и старших школьников учить понятиям «рекурсия» и «циклы» как можно раньше, просто и наглядно, например, используя табличный процессор Excel? Ответ — ДА! Excel является прекрасной средой для начального обучения программированию в школе и ВУЗе.

Видимо это утверждение не слишком охотно воспринимается опытными программистами, так как автор лекций «Основы офисного программирования и документы Excel» В.А. Биллиг на страницах Интернет-Университета Информационных Технологий пишет следующее: «Я высказываю и пытаюсь обосновать здесь

«крамольную» мысль о том, что Excel является прекрасной средой начального обучения программированию в школе и в вузах» [2].

Цель данной статьи — показать дидактические возможности Excel и целесообразность его использования при решении математических и практических задач по теме «Рекурсивные вычисления».

Итак, покажем, что применяя Excel можно освоить рекурсивный подход к решению математических и практических задач. Рассмотрим конкретные задачи на рекурсию и их реализацию в программе Excel.

Рекурсией в программировании называется ситуация, в которой какая-либо подпрограмма прямо или через другие подпрограммы вызывает себя в качестве подпрограммы. Реализуемый при этом алгоритм называется рекурсивным [4].

В математике очень часто встречаются последовательности чисел, в которых каждый следующий член выражается через предыдущие. Формулы, выражающие очередной член последовательности через один или несколько предыдущих членов, называют рекуррентными соотношениями.

В арифметической прогрессии, например, каждый следующий член равен предыдущему, увеличенному на разность прогрессии: a(i) = a(i-1) + d.

При вычислении факториала n!, который определяют как произведение первых n чисел натурального ряда n!=1*2*3*. *n, также можно использовать рекуррентное соотношение, в котором n! выражается через предыдущий (n-1)!, т.е. используется рекуррентная формула:

0!=1, для любого n>0 n!=n*(n-1)!

Аналогично при вычислении суммы ряда чисел S=1+2+3+. +n можно использовать рекуррентное соотношение:

ФІЗИКО-МАТЕМАТИЧНА ОСВІТА (ФМО)

S(1)=1, для любого n>0 S(n)=n+S(n-1)

Важное место в математике занимает последовательность чисел известная как ряд Фибоначчи, так как проявляется в самых неожиданных ее приложениях. Строгое определение этого ряда следующее: каждое число ряда, начиная со второго, равно сумме двух предыдущих. Вот эта задача в том виде, как формулирует ее сам Фибоначчи: «Пара кроликов через месяц производит на свет другую пару, а потомство они дают со второго месяца после своего рождения. Итак, через месяц будет две пары, через два месяца — три пары, а через четыре месяца — пять, так как к паре, рожденной первой парой, добавятся первые дети от второй пары. ». Продолжая процесс, получим количество пар кроликов по месяцам: 1, 1, 2, 3, 5, 8, 13, 21, 35, 56. эти числа и представляют ряд, названный по имени автора задачи [2].

Рекуррентные соотношения, определяющие вычисление чисел Фибоначчи: F(1) = 1; F(2) = 2; при k = 3. N F(k) = F(k-2) + F(k-1)

Наличие рекуррентного соотношения позволяет использовать рекурсию. Эти и другие задачи используются при обучении программированию в темах: циклы, рекурсия. Иногда их решение вызывает у студентов некоторые трудности, поскольку им приходится осваивать незнакомый язык программирования и одновременно логику программы. В табличном процессоре Excel эти задачи решаются наглядно просто и без программирования, путем создания и копирования формул на рабочем листе.

Это возможно благодаря тому, что одним из преимуществ Excel, его важной особенностью, является применяемый способ задания ссылок на ячейки в формулах. Excel позволяет задавать разные типы ссылок на ячейки: абсолютные, относительные и полуабсолютные. Относительные ссылки — это ссылки относительно положения самого объекта-формулы. Если изменяется положение формулы, то соответственно меняется и ячейка, на которую она ссылается. Ссылки на ячейки можно задавать в двух форматах: A1 и R1C1. По умолчанию ссылки в первом формате являются относительными. Так, например, ссылка F20 является относительной и при копировании формулы (смене положения формулы) будет определять другую ячейку, в зависимости от изменения первоначального положения формулы. Чтобы сделать ссылку абсолютной, нужно добавить символы $ перед именем столбца и индексом строки: $F$20, в этом случае при смене положения формулы на листе ссылка будет указывать на ту же самую ячейку. Пример полуабсолютной ссылки: F$20, $F20.

В формулах часто используются относительные ссылки в формате R1C1, в котором явно можно указывать смещение относительно объекта-формулы, например следующим образом: =RC[-2]*RC[-1], что означает перемножить ячейки, одна из которых находится в той же строке, но на два столбца левее от формулы, а другая в той же строке, но на один столбец левее от формулы. Правило записи таких ссылок легко понять из нижеследующей таблицы:

R Абсолютная ссылка на текущую строку

С Абсолютная ссылка на текущий столбец

R2C2 Абсолютная ссылка на ячейку, расположенную во второй строке и во втором столбце

R[-1] Относительная ссылка на строку, расположенную выше текущей ячейки

С[-1] Относительная ссылка на столбец, расположенный левее текущего столбца

ФІЗИКО-МАТЕМАТИЧНА ОСВІТА (ФМО) № 1(1), 2013

R[-2]C Относительная ссылка на ячейку, расположенную на две строки выше и в том же столбце

RC [-2] Относительная ссылка на ячейку, расположенную на два столбца левее и в той же строке

R[2]C[2] Относительная ссылка на ячейку, расположенную на две строки ниже и на два столбца правее

Стиль ссылок R1C1 полезен при вычислении положения столбцов и строк в макросах.

Рассмотрим программную реализацию задачи Фибоначчи в Excel с использованием модуля VBA. При указании ссылок в формуле (Formula) задано смещение по строкам, а столбец не указан, что по умолчанию предполагает использование столбца A объекта (Range). Относительные ссылки позволяют реализовать рекурсивные вычисления.

Range(«A1») = 1: Range(«A2») = 2 Range(«A3:A20»).Formula = «=R[-2]+R[-1]»

Однако та же задача совершенно естественно решается в Excel без всякого программирования. Достаточно записать значение 1 в ячейку A1, значение 2 — в ячейку A2, формулу «=A1+A2» — в ячейку A3, после чего скопировать формулу в нужный диапазон ячеек от A4 до A20. При копировании формулы будет учтена относительность ссылок, так что в ячейке A20 соответствующая формула будет иметь вид — «=A18+A19».

Аналогично можно решить задачи для факториала, суммы ряда чисел, вычислить члены арифметической или геометрической прогрессии. Пример рабочего листа Excel з формулами и результатами расчетов приведен на рис.1 и рис.2.

А В с D E F G Н I J

1 1 1 =С1 =ФАКТР(С1) 1 =G1 =СУММ(ЇЄЇ1 :G1)

2 2 2 =D1*C2 =ФАКТР(С2) 2 =G2+H1 -Cyiv1M($G$1 :G2)

3 =А1 +А2 3 =D2*C3 =ФАКТР(СЗ) 3 =G3+H2 -CyMM($G$1 :G3) =

4 =А2+А3 Ч 4 =D3*C4 =ФАКТР(С4) 4 =G4+H3 -CyMM($G$1 :G4)

5 =АЗ+А4 И 5 =D4*C5 =ФАКТР(С5) 5 =G5+H4 -CyMM($G$1 :G5) c —

6 =А4+А5 с 6 =D5*C6 =ФАКТР(С6) Ф 6 =G6+H5 -CyMM($G$1 :G6)

7 =А5+А6 л 7 =D6*C7 =ФАКТР(С7) А 7 =G7+H6 -CyMM($G$1 :G7) J

8 =А6+А7 а 8 =D7*C8 =ФАКТР(С8) К 8 =G8+H7 =CVMM($G$1:G3)

9 =А7+А8 9 =D8*C9 =ФАКТР(С9) Т 9 =G9+H8 =CVMM($G$1:G9)

10 =А8+А9 ф 10 =D9*C10 =ФАКТР(С10) 0 10 =G10+H9 =CVMM($G$1:G10)

11 =А9+А10 и 11 =D10*C11 =ФАКТР(С11) р 11 =G11+H10 -Cyiv1M($G$1 :G11)

12 =А10+А11 б 12 =D11*012 =ФАКТР(С12) и 12 =G12+H11 -СУММ(ЇСЇ1 :G12)

13 = А11+А12 0 13 =D12*C13 =ФАКТР(С13) А 13 =G13+H12 -Cyiv1M($G$1 :G13)

14 =А12+А13 н 14 =D13*C14 =ФАКТР(С14) Л 14 =G14+H13 -CyMM($G$1 :G14)

15 =А13+А14 а 15 =D14*C15 =ФАКТР(С15) 15 =G15+H14 -CyMM($G$1 :G15)

16 =А14+А15 ч 16 =D15*C16 =ФАКТР(С16) 16 =G16+H15 -CyMM($G$1 :G16)

17 =А15+А16 и 17 =D16*C17 =ФАКТР(С17) 17 =G17+H16 -CyMM($G$1 :G17)

18 =А16+А17 18 =D17*C18 =ФАКТР(С18) 18 =G18+H17 -CyMM($G$1 :G18)

19 = А17 +А18 19 =D18*C19 =ФАКТР(С19) 19 =G19+H18 -CVMM($G$1 :G19)

20 =А18+А19 20 =D19*020 =ФАКТР(С20) 20 =G20+H19 =CVMM($G$1:G20) r ■

ФІЗИКО-МАТЕМАТИЧНА ОСВІТА (ФМО)

А В С D Е F G Н I J А

1 1 1 1 1 1 1 1

2 2 2 2 2 2 Зг 3

3 3 3 6 6 3 6Г 6 =

4 5 Ч 4 24 24 4 10г 10

5 8 н 5 120 120 5 15 г 15 г —

6 13 с 6 720 720 Ф 6 21 г 21

7 21 л 7 5040 5040 А 7 28 г 28 У м м

8 34 а 8 40320 40320 К 8 36 г 36

9 55 9 362880 362880 Т 9 45 г 45

10 89 Ф 10 3628800 3628800 0 10 55 г 55

11 144 н 11 39916800 39916800 Р 11 66 г 66

12 233 б 12 479001600 479001600 И 12 78 г 78 Р

13 I 377 0 13 6227020800 6227020800 А 13 91 г 91 д

14 610 н 14 87178291200 87178291200 Л 14 105 г 105

15 987 а 15 1.30767 Е+12 1.30767Е+12 15 120 г 120

16 1597 ч 16 2.09228 Е+13 2.09228 Е+13 16 136 г 136

17 2584 н 17 3.55687 Е+14 3.55687 Е+14 17 153 г 153

18 4181 18 6.40237 Е+15 6.40237 Е+15 18 171 г 171

19 6765 19 1.21Є45Е+17 1.21Є45Е+17 19 190 г 190

20 10946 20 2.4329Е+18 2.4329Е+18 20 210 210 IV

Рис. 2. Результаты расчетов

5 =А4+1 =В4*$В$1/А5 =С4+В5

6 =А5+1 =В5*$В$1/А6 =С5+В6

7 =А6+1 =В6*$В$1/А7 =С6+В7

8 =А7+1 =В7*$В$1/А8 =С7+В8

9 =А8+1 =В8*$В$1/А9 =С8+В9

10 =А9+1 =В9*$В$1/А10 =С9+В10 =

11 =А10+1 =B10*SBS1/A11 =С10+В11

12 =А11 +1 =В1ГЇВЇ1/А12 =011 +В12

13 =А12+1 =В12*$В$1/А13 =С12+В13

14 =А13+1 =В13*$В$1/А14 =С13+В14

15 =А14+1 =B14*SBS1/A15 =С14+В15

16 =А15+1 =B15*SBS1/A16 =С15+В16

17 =А16+1 =В16*$В$1/А17 =С16+В17

18 =А17+1 =B17*SBS1/A18 =017 +В18

19 =А18+1 =B18*SBS1/A19 =018+В19

Рис. 3. Вычисление ex

Значение х заносим в ячейку В1, в дальнейшем используем абсолютную ссылку на эту ячейку $B$1 при подсчете A(k). Для значений k, A(k) и Sum(Ak) заносим в строку 4 базу рекурсии, в строку 5 — формулы рекуррентного соотношения, копируем эти формулы с помощью автозаполнения вниз. Для проверки в ячейку В2 занесем формулу расчета с использованием встроенной функции EXP(x).

Изменяя в ячейке В1 значение х можно увидеть как стремится к нулю текущий член суммы ряда, насколько точность вычислений зависит от количества членов ряда, как взаимосвязаны значения х и скорость сходимости ряда. Например, если учитывать 4 десятичных разряда, при х=2,5 ряд сходится с 12 члена (k=12), при х=3 с k=13, при х=5

ФІЗИКО-МАТЕМАТИЧНА ОСВІТА (ФМО)

с k=21 и т.д. Одним словом, можно исследовать поведение ряда и воочию увидеть закономерности изменения. Такой подход помогает легче понять и запомнить математические понятия и зависимости.

В каких же ситуациях требуется прибегать к циклическим вычислениям? Это следует делать, если речь идет о реализации итерационного процесса, вычислениях по рекуррентным соотношениям. Иногда приходится вводить формулы, в которых одна ячейка явно или неявно ссылается на саму себя, возникают циклические ссылки. Если не предпринять специальных мер, то циклические ссылки породят бесконечные вычисления. Excel следит за тем, возникают ли циклические ссылки, и в нормальном режиме не допускает таких вычислений, требуя скорректировать формулы так, чтобы циклов не было.

Однако можно включить специальный режим вычислений, допускающий циклические ссылки. В последнем случае требуется, чтобы число повторений цикла было конечным, только тогда Excel допускает переход к новому режиму, обеспечивающему проведение циклических вычислений. Для этого достаточно на вкладке Вычисления (меню Сервис, пункт Параметры) включить флажок Итерации и при необходимости изменить число повторений цикла в окошке «Предельное число итераций». Можно также задать погрешность вычислений в окошке «Относительная погрешность», что также приводит к ограничению числа повторений цикла. По умолчанию максимальное число итераций и погрешность вычислений соответственно имеют значения 100 и 0,001.

Необходимо также учитывать при решении таких задач особенности циклических вычислений, а именно:

1. Формулы, связанные циклическими ссылками, вычисляются многократно.

2. Размещение формул на листе определяет последовательность их вычисления. Формулы вычисляются сверху вниз, слева направо.

3. Число повторений цикла определяется параметрами, заданными на вкладке Вычисления.

4. Цикл заканчивается, когда изменения значений во всех ячейках не превосходят заданной погрешности или при достижении максимального числа итераций.

Рассмотрим пример практической задачи с использованием цикла для расчета сметы работ [1, с.316]:

Допустим необходимо рассчитать цену работ, если фонд заработной платы составляет 2 000 грн., запланированные средства на служебные командировки -200 грн., затраты на материалы — 150 грн. При этом отчисления (налог) в фонд социального страхования составляет 37% заработной платы. В расчет цены закладывается прибыль предприятия — 10% от цены работ, а также накладные затраты — 10% и другие прямые затраты 2,2% от цены работ. Решения задачи в Excel показано на рис.4.

В данном примере встречается неявная циклическая ссылка: значение ячейки С9 рассчитывается как сумма ячеек С2:С8, часть из которых в свою очередь зависят от С9. Формулы в ячейках С4, С7-С9 содержат рекурсию. В обычном режиме работы Excel по данным формулам невозможно провести вычисления, программа выдает сообщение об ошибке — циклической ссылке. После перехода к новому режиму, допускающему циклические ссылки, получаем представленный на рис.5 результат.

ФІЗИКО-МАТЕМАТИЧНА ОСВІТА (ФМО)

1 Статті витрат % Сума _

2 Заробітна плата 2000

3 Відрахування на соц. Страхування 0,37 =С2*ВЗ

4 Накладні витрати 0,15 =С9*В4

5 Матеріали 150

6 Витрати на службові відрядження 200

7 Інші прямі витрати 0,022 =С9*В7

8 Прибуток 0,1 =С9*В8

9 Л П Ціна =СУММ(С2:С8) і 1 —

Рис. 4. Расчет сметы работ. Формулы Рабочего Листа

1 Статті витрат % Сума І

2 Заробітна плата 2 000,00 грн.

3 Відрахування на соц. Страхування 37% 740,00 грн.

4 Накладні витрати 15% 636,68 грн.

5 Матеріали 150,00 грн.

6 Витрати на службові відрядження 200,00 грн.

7 Інші прямі витрати 2,20% 93,38 грн.

8 Прибуток 10% 424,45 грн.

9 Ціна 4 244,51 грн.

Рис. 5. Результаты расчета сметы работ

Эта и подобные ей задачи часто встречаются в реальной жизни предпринимателей, бизнесменов, бухгалтеров, экономистов, и на помощь им приходит такой простой, доступный инструмент для подобных вычислений каким является Excel. Как видим, не только математические задачи приходится решать с помощью рекурсии и циклов, не только математикам и программистам необходимо понимание рекурсивных алгоритмов.

Из всего выше изложенного можно сделать выводы.

Преимущества табличного процессора Excel для обучения понятию «рекурсия» состоят в следующем:

o Excel идеально приспособлен к тому, чтобы простые рекурсивные вычисления, заданные рекуррентными соотношениями, определялись почти автоматически. В Excel при копировании формул ссылки на переменные меняются автоматически, благодаря этому реализуются рекуррентные соотношения. Достаточно скопировать формулу, чтобы реализовать рекурсивное вычисление.

о Достаточно сложные на начальном этапе обучения задачи решаются без программирования, путем задания и копирования формул на рабочем листе. Это важно для поэтапного обучения.

o Простые рекурсивные вычисления приобретают необходимую наглядность так, что ничего не остается скрытым. Можно видеть, как меняется формула, тут же в ячейке видеть значение, рассчитанное по этой формуле.

о При решении многих задач появляется совершенно новое качество, крайне важное для обучения — показан процесс решения, а не только конечный результат. Решение позволяет наглядно видеть, как сходится процесс вычислений, изучать влияние аргумента на скорость сходимости. Такое подход способствует тому, чтобы стать исследователем, вместо того, чтобы оставаться простым наблюдателем.

ФІЗИКО-МАТЕМАТИЧНА ОСВІТА (ФМО)

Рекурсивные алгоритмы и их вычисления в Excel могут служить весьма подходящим фоновым материалом для начального освоения рекурсии как достаточно общего и эффективного метода решения задач. Примеры решения задач, рассмотренные в данной статье, заставляют по-новому оценить дидактические возможности табличного процессора Excel и осознать его роль и место в построении современного курса информатики в педагогических вузах.

Задачи, которые приведены в данной статье, используются в лабораторной работе по курсу «Решение математических задач средствами Excel».

Список использованных источников

1. Баженов В.А., Венгерський П.С. Інформатика. Комп’ютерна техніка. Комп’ютерні технології. — К.: Каравелла, 2008. — 640 с.

2. Биллиг В.А Основы офисного программирования и документы Excel http://www.intuit.rU/department/office/vbaexcel/1/.

3. Добровольский Н.М., Есаян А.Р., Пихтильков С. A., Стеценко В.Я. Об одном вычислительном эксперименте. Межвузовский сборник статей. Ч.1-Тула: Изд-во Тул. гос. пед. ун-та, 1999.10 с.

4. Есаян А.Р. Фракталы и рекурсия. Учеб. пособие для студентов педвузов. — Тула, 1999. -52с.

Аннотация. Шамшина Н. Использование табличного процессора MS Excel при решении задач на рекурсию.

Табличный процессор Excel целесообразно использовать для решения задач на рекурсию, чтобы освоить рекурсивный подход к решению математических и практических задач.

Ключевые слова: табличный процессор MS Excel, рекурсия, решение задач.

Анотація. Шамшина Н. Використання табличного процесора MS Excel при розв’язуванні задач на рекурсію.

Табличний процесор Excel доцільно використовувати для розв’язування задач на рекурсію, щоб засвоїти рекурсивний підхід до розв’язування математичних і практичних задач.

Ключові слова: табличний процесор MS Excel, рекурсія, розв’язування задач.

Abstract. Shamshyna N. Using MS Excel spreadsheet to solve problems on recursion.

Excel spreadsheet useful for solving problems on recursion to learn a recursive approach to solving mathematical and practical problems.

Keywords: spreadsheet MS Excel, recursion, solving problems.

Видео:15. Однородная система линейных уравнений / фундаментальная система решенийСкачать

Excel. Использование циклических ссылок для решения уравнений итерационным способом

Ранее я описал, как найти и исправить циклическую ссылку. Напомню, что циклическая ссылка появляется, если в ячейку Excel введена формула, содержащая ссылку на саму эту ячейку (напрямую или через цепочку других ссылок). Например (рис. 1), в ячейке С2 находится формула, ссылающаяся на саму ячейку С2.

Рис. 1. Пример циклической ссылки

Но. Не всегда циклическая ссылка является бедствием. Циклическую ссылку можно использовать для решения уравнений итерационным способом. Для начала нужно позволить Excel вести вычисления, даже при наличии циклической ссылки. В обычном режиме Excel, обнаружив циклическую ссылку, выдаст сообщение об ошибке, и потребует ее устранения. В обычном режиме Excel не может провести вычисления, так как циклическая ссылка порождает бесконечный цикл вычислений. Можно, либо устранить циклическую ссылку, либо допустить вычисления по формуле с циклической ссылкой, но ограничив число повторений цикла. Для реализации второй возможности щелкните на кнопке «Office» (в левом верхнем углу), а затем на «Параметры Excel» (рис. 2).

Скачать заметку в формате Word, примеры в формате Excel

Рис. 2. Параметры Excel

В открывшемся окне «Параметры Excel» перейдите на вкладку Формулы и отметьте «Включить итеративные вычисления» (рис. 3). Помните, что эта опция включается для приложения Excel в целом (а не для одного файла), и будет действовать, пока вы ее не отключите.

Рис. 3. Включить итеративные вычисления

На этой же вкладе, можно выбрать, как будут вестись вычисления: автоматически или вручную. При автоматическом вычислении Excel сразу рассчитает конечный результат, при вычислениях, вручную, можно будет наблюдать результат каждой итерации (простым нажатием F9 запуская каждый новый цикл вычисления).

Решим уравнение третьей степени: х 3 – 4х 2 – 4х + 5 = 0 (рис. 4). Для решения этого уравнения (и любого другого уравнения совершенно произвольного вида) понадобится всего одна ячейка Excel.

Рис. 4. График функции f(x)

Для решения уравнения нам понадобится рекуррентная формула (то есть, формула, выражающая каждый член последовательности через один или несколько предыдущих членов):

(1) x = x – f(x)/f’(x), где

f(x) – функция, задающая уравнение, корни которого мы ищем; f(x) = х 3 – 4х 2 – 4х + 5

f’(x) – производная нашей функции f(x); f’(x) = 3х 2 – 8х – 4; производные основных элементарных функций можно посмотреть здесь.

Если вы заинтересовались, откуда взялась формула (1), можете почитать, например, здесь.

Итоговая рекуррентная формула имеет вид:

(2) х = x – (х 3 – 4х 2 – 4х + 5)/(3х 2 – 8х – 4)

Выберем любую ячейку на листе Excel (рис. 5; в нашем примере это ячейка G19), присвоим ей имя х, и введем в нее формулу:

Можно вместо х использовать адрес ячейки… но согласитесь, что имя х, смотрится привлекательнее; следующую формулу я ввел в ячейку G20:

Рис. 5. Рекуррентная формула: (а) для поименованной ячейки; (б) для обычного адреса ячейки

Как только мы введем формулу и нажмем Enter, в ячейке сразу же появится ответ – значение 0,77. Это значение соответствует одному из корней уравнения, а именно второму (см. график функции f(x) на рис. 4). Поскольку начальное приближение не задавалось, итерационный вычислительный процесс начинался со значения, по умолчанию хранимого в ячейке х и равного нулю. Как же получить остальные корни уравнения?

Для изменения стартового значения, с которого рекуррентная формула начинает свои итерации, предлагается использовать функцию ЕСЛИ: [1]

Здесь значение «-5» – начальное значение для рекуррентной формулы. Изменяя его, можно выйти на все корни уравнения:

Начальное значение	Корень уравнения
1	0,77
-5	-1,40
8	4,63

[1] Идея подсмотрена здесь

Видео:Решение уравнений с помощью ExcelСкачать

7 комментариев для “Excel. Использование циклических ссылок для решения уравнений итерационным способом”

Офигенный сайт!
И как всегда когда не нужно все находишь!
Блин у меня по экономическому моделированию в Excell курсовик был в институте, вот время помню кучу потерял а тут все в одном флаконе:)
Все равно инфа пригодится, даже очень!

И нам зараза в этом гребанном институте мать их так этих учителей даже близко ничего подобного не рассказывали. Я не про этот пример говорю а про остальные..
«Вычисление стандартного отклонения для данных с тенденцией», «Нормальное распределение» и т.п.. даже объяснить не могли или не хотели как это все применять, а тут все наглядно и понятно! Огромное спасибо! Не зря я на этот сайт наткнулся, чую он мне еще окажет неплохую помощь))))

В упор не понимаю откуда берется предел для определения корней уравнения, если «Здесь значение «-5» – начальное значение для рекуррентной формулы. Изменяя его, можно выйти на все корни уравнения»

У меня график получается, который с осью Х не имеет вообще пересечений, мож где накосячила?
Пожалуйста подскажите, а то у меня взрыв мозга будет скоро…((((

Тамара, если Вы строите график на основе моих данных, откройте файл Excel; если Вы используете собственные данные, пришлите мне на mail Ваш файл, попробую помочь))

Спасибо заранее за беспокойство, вот такое уравнение у^3-20у^2-158у-420=0, если не трудно объясните пожалуйста как вы определяте предел в каких знчениях надо считать корни.

Видео:Матричный метод решения систем уравненийСкачать

Продвинутый взгляд на рекурсию

Рекурсия является одним из наиболее мощных подходов в программировании. С ее помощью можно решать чрезвычайно сложные задачи, печатая при этом невероятно малый объем кода. Тем не менее понимание данного принципа нередко вызывает сложности, поскольку для этого требуется нестандартный взгляд на процесс выполнения команд.

Сложность примеров, описанных в данной статье, будет возрастать постепенно, начиная от самых простых и заканчивая достаточно трудными. При этом каждый из них будет сопровождаться подробной диаграммой:

Рекурсивный способ мышления.
Рекуррентные соотношения.
Мемоизация.
Стратегия “разделяй и властвуй”.

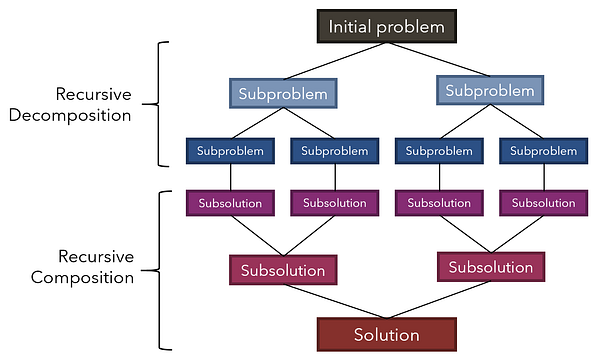
Рекурсия используется для решения задач, в которых функция вызывает сама себя в рамках собственного определения. В каждой реализации рекурсии должно присутствовать два элемента:

Заключительный базовый кейс или кейсы, в которых рекурсивный поиск ответа более не производится.
Набор правил (рекуррентных соотношений), который инициирует очередные циклы рекурсии, сводя таким образом общие кейсы к базовому.

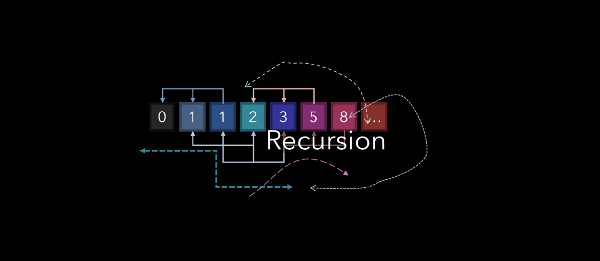
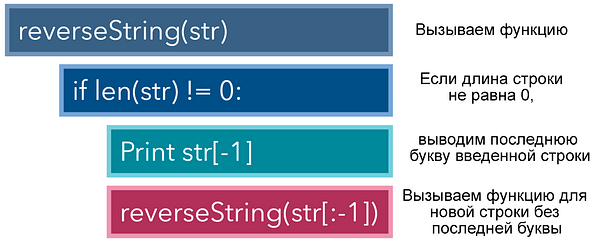
В качестве примера давайте рассмотрим задачу по выводу развернутого варианта строки. В этом случае на выходе из вводного слова ‘hello’ должно получиться ‘olleh’. Итеративный метод решения этой задачи — применение цикла for и вывод каждого знака, начиная с последнего и заканчивая первым.

В рекурсивном же подходе мы сначала создаем функцию reverseString , получающую интересующую нас строку в качестве параметра. Если длина ввода не равна 0, то такой кейс является базовым или заключительным, и мы выводим последнюю букву, а затем инициируем еще один экземпляр reverseString для той же строки, исключив последнюю букву, поскольку ее мы уже вывели.

Обратите внимание: поскольку функция вызывается изнутри себя, она сама создает цикл for . Кроме того, наличие инструкции if перед вызовом другого экземпляра функции обязательно, в противном случае будет выброшена ошибка RecursionError или RuntimeError , поскольку скрипт не увидит конца бесконечного цикла. Данная ситуация аналогична бесконечному циклу While True .

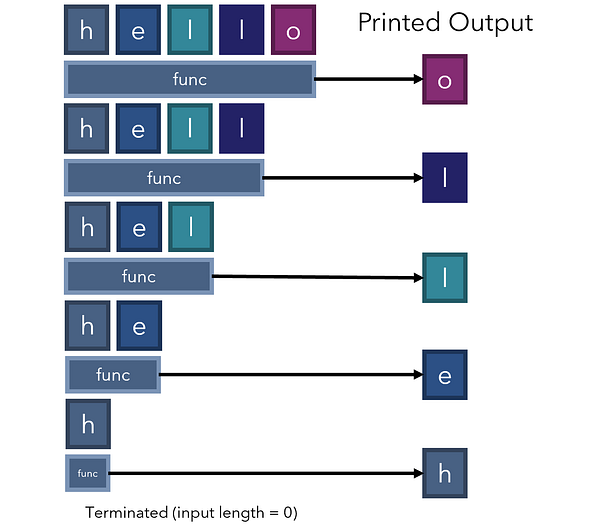
Давайте посмотрим, как эта рекурсивная функция работает с ‘hello’:

Рекуррентность в более сложных задачах может вызвать трудности при определении двух ее компонентов — рекуррентного соотношения, т.е. соотношения между результатом задачи и результатом ее подзадач и базовым кейсом, представляющим кейс, который можно вычислить напрямую без дополнительных рекурсивных вызовов. Иногда базовые кейсы называются “нижними кейсами”, потому что они являются кейсами, в которых задача уменьшена до наименьшего масштаба.

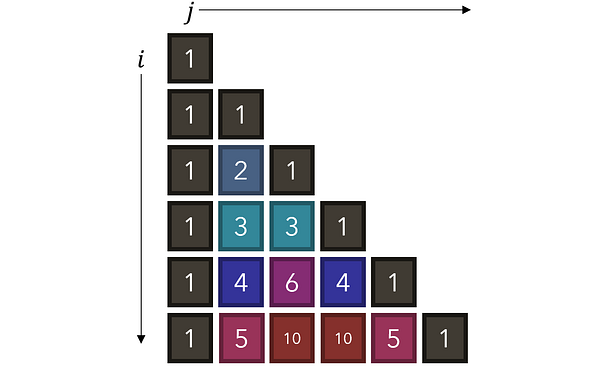
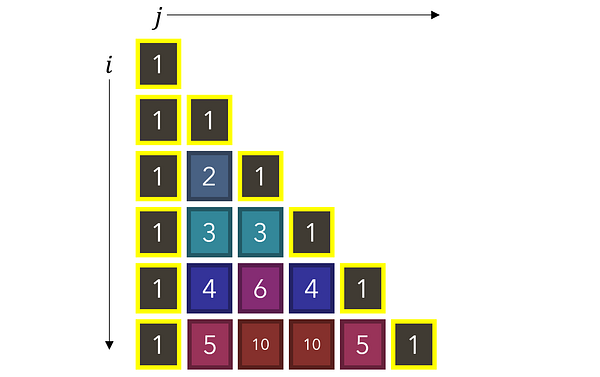
Рассмотрите в качестве примера треугольник Паскаля, в котором каждое число является суммой двух, находящихся над ним, и который имеет по сторонам единицы. Как можно использовать рекурсию для нахождения значения любого значения в точке (i, j)? Каково будет рекуррентное соотношение и базовый/заключительный кейс?

Рекуррентное соотношение можно выразить следующим уравнением:

Это очевидно, когда смотришь на график треугольника. Еще более примечательно в этой формуле то, что если мы продолжим с ее помощью разбивать любую точку (i, j) на сумму двух других точек, то в итоге неизбежно получим базовый кейс — 1. Треугольник Паскаля начинается с единиц, и из их сумм строится весь сложный паттерн.

Как же нам это реализовать?

Для начала давайте найдем набор правил, чтобы определять, когда выполняется базовый кейс, при котором значение ячейки равняется 1. Обратите внимание, что 1-цы появляются при выполнении одного из двух условий: когда располагаются либо в первом столбце (j=0), либо по диагонали (i=j).

Теперь выполнить реализацию просто. Если условия для базового кейса выполнены, мы возвращаем базовое значение (1). В противном случае мы продолжаем уменьшать задачу до тех пор, пока не достигнем базового кейса, до которого, как мы определили, будет неизбежно разбит любой ввод.

Теперь рекурсия раскрылась для вас во всей красе. Здесь, с помощью всего пяти строк кода, мы, по сути, создаем саморазвивающееся дерево. При желании число строк кода можно даже уменьшить до трех. Вызывая функцию pascal дважды, мы инициируем две ветви поиска, каждая из которых также инициирует еще две, предполагая, что базовый кейс достигнут не был.

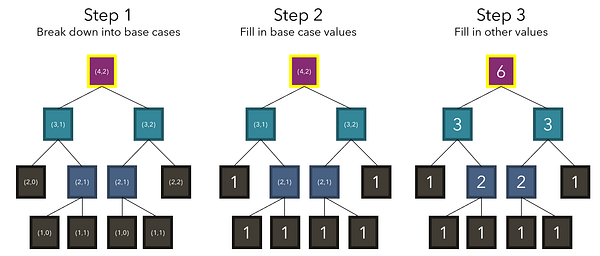
Такая эффективность рекурсии может показаться магической и даже может запутать. Давайте рассмотрим работу ее алгоритма на примере.

В соответствии с нашим рекуррентным соотношением (4, 2) разбивается на (3, 1) и (3, 2), которые являются двумя числами, стоящими над ней. Обратите внимание, что алгоритм на деле не знает, что значения этих ячеек представлены 3. Он просто учитывает их местоположение. Мы не знаем или даже не интересуемся никакими значениями, пока выполняются базовые условия. На основе базовых кейсов (1) мы можем вычислить другие не базовые точки, но для начала должны быть найдены все базовые.

Согласно нашему рекуррентному соотношению, кейсы итеративно разбиваются до тех пор, пока не достигается базовый (j = 0 или i = j). Поскольку нам известны значения этих базовых кейсов (1), мы можем заполнить и другие значения, зависимые от базового кейса.

Это, конечно же, очень, а возможно и чересчур подробное представление принципа работы рекурсивного алгоритма. В действительности ни один из этих трех шагов не нужно программировать, так как они выполняются скриптом автоматически. Все, что вам нужно, — это вызвать функцию внутри ее самой и обеспечить ее завершение в некоторых точках при достижении базового случая.

При вызове return pascal(i-1, j) + pascal(i-1, j-1) мы рассматриваем возврат не как процесс, а как число. Поскольку pascal(i-1, j) инициирует собственные процессы ветвления, а в итоге возвращает другое число (например, 3), будет правильным воспринимать его именно как число, а не как процесс, что может вызвать ненужную сложность и затруднение в понимании.

С некоторой точки зрения этот рекурсивный алгоритм можно назвать неэффективным. В конце концов ‘6′ разбивается на ‘3′, которое, с позиции значения, имеет идентичные разбивки, но при этом зачем-то вычисляется второй раз. Это стандартный случай в рекурсии, когда базовые кейсы одного кейса, будучи вычисленными ранее, вычисляются повторно. Для устранения этой проблемы мы используем мемоизацию.

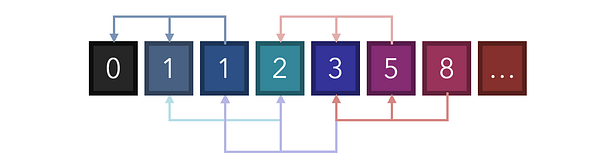
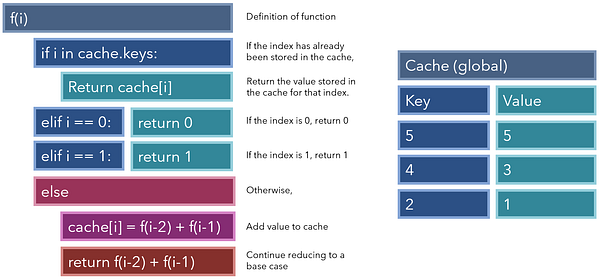
Возьмите в качестве примера последовательность Фибоначчи, в которой первые два числа представлены 0 и 1, а последующие числа являются суммой двух, им предшествующих. На основе уже сформированного знания мы понимаем, что базовыми кейсами здесь будут 0 и 1, а рекуррентное соотношение будет выглядеть как v(i) = v(i-2) + v(i-1). В таком случае мы можем построить простую рекурсивную функцию для нахождения значения последовательности Фибоначчи в любом индексе, начиная с 0.

Обратите внимание, что хоть это и грамотное применение рекурсии, оно весьма неэффективно. 8 разбивается на 3 и 5, а 5, в свою очередь, разбивается на 3 и 2. Мы вычисляем все с самого начала и строим завершенное дерево поиска со множеством повторений.

С помощью мемоизации мы можем решить эту проблему, создав кэш. Это можно реализовать, используя словарь и сохраняя значения, заданные ранее. Например, когда индекс 6 (значение 8) разбивается на индекс 4 и индекс 5 (значения 3 и 5), мы можем сохранить значение индекса 4 в кэше. При вычислении индекса 5 как индекса 3 плюс индекс 4 мы можем извлечь индекс 4 из кэша вместо того, чтобы повторно вычислять его, создавая еще одно обширное дерево, ведущее к базовым кейсам.

Чтобы включить в нашу функцию мемоизацию, мы добавим две функциональности: во-первых, если текущий индекс был сохранен в кэше, мы будем просто возвращать его сохраненное значение; во-вторых, прежде чем продолжать уменьшать значение, мы будем добавлять это значение к кэшу,чтобы ускорить дальнейшие операции. Обратите внимание, что кэш должен быть либо глобальной переменной, либо такой, которую можно извлечь и изменить независимо от области вызова команды.

После добавления мемоизации наша рекурсивная функция стала намного быстрее и мощнее.

Рекурсия занимает центральное место среди многих наибыстрейших алгоритмов сортировки. Цель этих алгоритмов — получить список чисел и вернуть их в порядке от меньшего к большему. Поскольку очень много приложений опираются на быструю сортировку, весьма важно найти такой, который сможет сортировать списки максимально быстро. При этом некоторые из самых быстрых алгоритмов используют рекурсивный подход, называемый “разделяй и властвуй”.

В стратегии “разделяй и властвуй” изначальная задача рекурсивно разбивается на несколько подзадач. После того, как каждая подзадача достигает размера единицы (аналог базового кейса), выявляются их подрешения, которые вновь рекурсивно совмещаются для формирования окончательного решения.

Рассмотрите, к примеру, QuickSort — один из наиболее быстрых алгоритмов сортировки, который при грамотной реализации может выполняться в 2–3 раза быстрее своих соперников и предшественников.

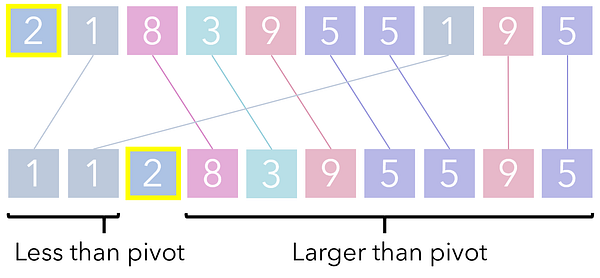
QuickSort начинает выполнение с выбора “опоры”. В простейших реализациях и для наших целей такую опору можно выбрать произвольно. Однако в более специализированных реализациях к ее выбору уже стоит подходить осторожно.

Все элементы со значениями меньше опоры переносятся левее нее, а все, чьи значения больше — правее. Выполнить это можно, пройдя по каждому элементу и переместив те, что меньше опоры, в один список, а те, что больше нее — в другой. Заметьте, что эта операция справляется с задачей только частично.

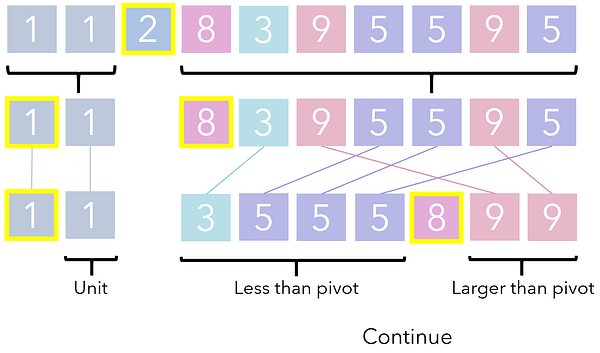
Процесс сортировки списка на основе его опорной точки называется разделением, так как опора разделяет этот список на два раздела, иначе говоря, на две стороны. Каждый их этих разделов вызывает очередную итерацию разделения сам на себя и так продолжается до тех пор, пока раздел не достигнет базового кейса (1 единицы, просто одного числа)

После достаточного числа рекурсивных вызовов исходный список будет разделен до точки, когда эти вызовы продолжить уже невозможно. В этой точке композиция подрешений выполняется простым составлением их в горизонтальном порядке. Результат такой композиции — отсортированный список.

Обратите внимание, что QuickSort следует многим из перечисленных основ рекурсии, рассмотренных нами ранее, только на более высоком уровне. Рекуррентное соотношение является разделением компонента, а базовый кейс — это разделение размера 1. Начиная с оригинального списка, те же процессы (выбор опоры и разделение) вызываются рекурсивно до тех пор, пока результат не будет состоять только из базовых кейсов.