Как рассчитать производные в Python? В этой статье мы будем использовать Sympy Sympy Python, чтобы играть с производными.
- Автор записи
Автор: Pankaj Kumar
Дата записи
- Производные в Python с использованием симпы
- Какие производные?
- Решение производных в Python с использованием Sympy
- 1. Установите Sympy, используя PIP
- 2. Решение дифференциала с Sympy Diff ()
- 3. Решение производных в Python
- Основные производные правила в Python Sympy
- 1. Правило питания
- 2. Правило продукта
- 3. Правило цепочки
- Производные многомерные функции с использованием Sympy
- Заключение
- Вычисление производной
- Подключение SymPy
- Формула российских дорог
- Дорога в горку
- Дорога с колеёй
- Руководство по SciPy: что это, и как ее использовать
- Что такое SciPy?
- NumPy vs SciPy
- Пакеты в SciPy
- Базовые функции
- Взаимодействие с NumPy
- Специальные функции
- Экспоненциальные и тригонометрические функции
- Интегральные функции
- Двойные интегральные функции
- Функции оптимизации
- Функция Розенброка
- Nelder-Mead
- Функции интерполяции
- Одномерная интерполяция
- Многомерная интерполяция
- Функции преобразования Фурье
- Функции обработки сигналов
- Линейная алгебра
- Нахождение обратной матрицы
- Нахождение определителей
- Разреженные собственные значения
- Разреженные структуры данных и алгоритмы
- Триангуляции Делоне
- Функции многомерной обработки изображений
Видео:Python - численное решение дифференциального уравнения 1го порядка и вывод графикаСкачать

Производные в Python с использованием симпы
Как рассчитать производные в Python? В этой статье мы будем использовать Sympy Sympy Python, чтобы играть с производными.
Видео:Уравнения в частных производных первого порядка| poporyadku.schoolСкачать
Какие производные?
Производные являются фундаментальными инструментами исчисления. Это очень полезно для оптимизации функции потери с Градиентный спуск в Машинное обучение возможно только из-за производных.
Предположим, у нас есть функция y = F ( X ), который зависит от х Затем вывод этой функции означает скорость, при которой значение y функции изменяется с изменением х Отказ
Это ни отнюдь означает статью о основах производных, она не может быть. Исчисление – это другой зверь, который требует особого внимания. Я предполагаю, что у вас есть какой-то опыт в исчислении. Эта статья предназначена для продемонстрирования того, как мы можем дифференцировать функцию с использованием симпы-библиотеки.
Видео:Сеточные методы решения дифференциальных уравнений в частных производных.Скачать

Решение производных в Python с использованием Sympy
Sympy – библиотека Python для символической математики.
Он стремится стать полнофункциональной системой компьютерной алгебры (CAS), сохраняя максимально простую код, остынет, не так ли.
1. Установите Sympy, используя PIP
Sympy имеет больше используемых, чем просто расчет производных, но на данный момент мы сосредоточимся на производных.
Беги PIP Установить Sympy Для установки с помощью Диспетчер пакетов PIP Отказ
2. Решение дифференциала с Sympy Diff ()
Для дифференциации Sympy предоставляет нам Различать способ вывода производной функции.
- Предположим, у нас есть функция: F ( x ) = х ²
- Производное функции w.r.t x: f ‘(x) = 2x.
Посмотрим, как мы можем достичь этого, используя Sympy.
Объявление символа похоже на то, что наша функция имеет переменную «X» или просто функция зависит от x.
3. Решение производных в Python
Теперь для расчета производной функции на Sympy есть лямбдифицировать Функция, в которой мы передаем символ и функцию.
Видео:Численные методы (1 урок)(Решение нелинейных уравнений. Метод дихотомии. Python)Скачать

Основные производные правила в Python Sympy
Есть определенные правила, которые мы можем использовать для расчета производной дифференцируемых функций.
Некоторые из наиболее встречающихся правил:
- Правило питания
- Правило продукта
- Правило цепи
- Цитал правило
Давайте погрузимся в то, как мы можем использовать Simpy для расчета производных, подразумеваемых правилами общей дифференцировки.
1. Правило питания
В общем: f ‘(x n ) (N-1)
Пример, функция у нас есть:
Это производное будет: (5-1) 4.
2. Правило продукта
Пусть u (x) и v (x) будут дифференцируемыми функциями. Тогда продукт функций u (x) v (x) также дифференцируемый.
Пример: (x) * cos (x)
3. Правило цепочки
Правило цепочки рассчитывает производное состав функций.
- Скажем, у нас есть функция (G (x))
- Затем в соответствии с правилом цепи: ‘(g (x)) g’ (x)
- Пример: (х ** 2)
Этот процесс может быть расширен для коэффициента правила также. К настоящему времени необходимо очевидно, что только функция меняется, в то время как процесс приложения остается прежним, остальное заботится о самой библиотеке.
Видео:Лукьяненко Д. В. - Численные методы - Лекция 18Скачать

Производные многомерные функции с использованием Sympy
Примеры, которые мы видели выше, имели одну переменную. Но мы более склонны столкнуться с функциями, имеющими более одной переменной в них. Такие производные, как правило, называются частичными производными.
Частичное производное многомерной функции представляет собой производное относительно одной переменной со всеми другими переменными.
Пример: f (x, y) 4 + х * у 4
Давайте частично отличаем вышеупомянутые производные в Python W.r.t x
Мы используем Символы Метод, когда количество переменных составляет более 1. Теперь, дифференцируйте производные в Python частично W.R.T Y
Код точно похоже, но теперь Y передается как аргумент ввода в Различать метод.
Мы можем выбрать частично дифференцировать функцию сначала w.r.t x, а затем y.
Видео:34 Задача: Найти корни квадратного уравнения при помощи PythonСкачать

Заключение
Эта статья ни в коем случае не было дискурсом о производных или как мы можем решать производные в Python, но статью о том, как мы можем использовать пакеты Python для выполнения разграничения на функции. Производные потрясающие, и вы обязательно должны получить идею позади него, так как они играют решающую роль в машинном обучении и за его пределами.
Видео:Вычислительная математика 18 Численные методы решения уравнений в частных производныхСкачать

Вычисление производной
Для вычисления производных будем использовать библиотеку SymPy. Это библиотека с открытым исходным кодом, полностью написанная на языке Python. Разрабатывается как система компьютерной алгебры.
Видео:Библиотека SymPy для алгебраических операций в PythonСкачать

Подключение SymPy
Вначале нам необходимо установить библиотеку. Для этого в терминале (командной строке) следует ввести команду: pip install sympy .
Для подключения библиотеки в коде на Python 3 следует использовать ключевое слово import .
Чтобы не писать перед всеми функциями sympy с точкой, подключу следующим образом:
Следует обратить внимание, что в SymPy объявлено множество классов и функций, имена которых могут пересекаться с названиями в других библиотеках. Например, если используете библиотеку math, то там также есть sin , cos , pi и другие.
Видео:Использование библиотеки SymPy для работы с системами уравнений в PythonСкачать

Формула российских дорог
Например, возьмем функцию с двумя независимыми переменными, типа поверхности y=f(x, z). Воспользуемся формулой российских дорог: y=sin(x)+0,5·z.
Перед тем как взять производную этой функции в Python, надо объявить все переменные, которые будут использоваться в ней. Для этого следует воспользоваться функцией symbols . В качестве аргумента используем строку с перечисленными через запятую или пробел названиями переменных.
После этого берем частную производную в Python 3 с помощью функции diff . Первым аргументом пишем функцию, вторым – переменную, по которой будем её дифференцировать.
Результат выводим с помощью print .
Дорога в горку
Возьмём производную по z:
В результате получили 0.5. Частная производная по z положительна, следовательно, дорога в горку.
Дорога с колеёй
Теперь возьмём производную по x:
Получили, что частная производная по x равна cos(x). Трактору на колею наплевать, ему важен только наклон горки.
В зависимости от задачи берем производную по нужному параметру.
В функции diff при необходимости, можно указать третьим параметром порядок дифференцирования. Так как мы вычисляли производную первого порядка, то его не указывали.
Видео:01.02. Модель SIR. Численное решение системы дифференциальных уравнений с помощью SciPyСкачать

Руководство по SciPy: что это, и как ее использовать
Математика — это масса понятий, которые являются одновременно важными и сложными. Для работы с ними в Python есть библиотека SciPy. В этом материале вы познакомитесь с ее функциями на примерах.
Видео:Лукьяненко Д. В. - Численные методы - Лекция 27Скачать

Что такое SciPy?
SciPy — это библиотека Python с открытым исходным кодом, предназначенная для решения научных и математических проблем. Она построена на базе NumPy и позволяет управлять данными, а также визуализировать их с помощью разных высокоуровневых команд. Если вы импортируете SciPy, то NumPy отдельно импортировать не нужно.
Видео:Лукьяненко Д. В. - Численные методы - Лекция 23Скачать

NumPy vs SciPy
И NumPy, и SciPy являются библиотеками Python, которые используются для математического и числового анализов. NumPy содержит данные массивов и операции, такие как сортировка, индексация, а SciPy состоит из числового кода. И хотя в NumPy есть функции для работы с линейной алгеброй, преобразованиями Фурье и т. д., в SciPy они представлены в полном виде вместе с массой других. А для полноценного научного анализа в Python нужно устанавливать и NumPy, и SciPy, поскольку последняя построена на базе NumPy.
Видео:Решение ОДУ 2 порядка в PythonСкачать

Пакеты в SciPy
В SciPy есть набор пакетов для разных научных вычислений:
| Название | Описание |
|---|---|
| cluster | Алгоритмы кластерного анализа |
| constants | Физические и математические константы |
| fftpack | Быстрое преобразование Фурье |
| integrate | Решения интегральных и обычных дифференциальных уравнений |
| interpolate | Интерполяция и сглаживание сплайнов |
| io | Ввод и вывод |
| linalg | Линейная алгебра |
| ndimage | N-размерная обработка изображений |
| odr | Метод ортогональных расстояний |
| optimize | Оптимизация и численное решение уравнений |
| signal | Обработка сигналов |
| sparse | Разреженные матрицы |
| spatial | Разреженные структуры данных и алгоритмы |
| special | Специальные функции |
| stats | Статистические распределения и функции |
Подробное описание можно найти в официальной документации.
Эти пакеты нужно импортировать для использования библиотеки. Например:
Прежде чем рассматривать каждую функцию в подробностях, разберемся с теми из них, которые являются одинаковыми в NumPy и SciPy.
Видео:Лукьяненко Д.В. - Параллельные вычисления - 10.Решение задач для уравнений в частных производных.Ч.3Скачать

Базовые функции
Взаимодействие с NumPy
SciPy построена на базе NumPy, поэтому можно использовать функции последней для работы с массивами. Чтобы узнать о них подробнее, используйте функции help() , info() или source() .
help():
Функция help() подойдет для получения информации о любой функции. Ее можно использовать двумя способами:
Вот пример для обоих:
При исполнении этого кода, первая help() вернет информацию о подмодуле cluster . А вторая — попросит пользователя ввести название модуля, ключевого слова и др., о чем требуется предоставить дополнительную информацию. Для выхода достаточно ввести quit и нажать Enter.
info():
Эта функция возвращает информацию о конкретных функциях, модулях и так далее.
source():
Исходный код можно получить только для тех объектов, которые были написаны на Python. Функция не вернет ничего важного, если методы или объекты были написаны, например, на C. Синтаксис простой:
Видео:Решение ОДУ в PythonСкачать

Специальные функции
SciPy предоставляет набор специальных функций, используемых в математической физике: эллиптические настраиваемые функции, гамма, бета и так далее. Для их поиска нужно использовать функцию help() .
Экспоненциальные и тригонометрические функции
Набор специальных функций SciPy включает такие, с помощью которых можно искать экспоненты и решать тригонометрические задачи.
Есть и масса других функций из SciPy, с которым стоит познакомиться.
Видео:Метод Ньютона (метод касательных) Пример РешенияСкачать

Интегральные функции
Есть и функции для решения интегралов. В их числе как обычные дифференциальные интеграторы, так и методы трапеций.
В SciPy представлена функция quad , которая занимается вычислением интеграла функции с одной переменной. Границы могут быть ±∞ (± inf ) для обозначения бесконечных пределов. Синтаксис этой функции следующий:
А здесь она внедрена в пределах a и b (могут быть бесконечностями).
В этом примере функция a находится в пределах 0 и 1. После выполнения вывод будет такой:
Двойные интегральные функции
SciPy включает также и dblquad , которая используется для вычисления двойных интегралов. Двойной интеграл, как известно, состоит из двух реальных переменных. Функция dblquad() принимает функцию, которую нужно интегрировать, в качестве параметра, а также 4 переменных: две границы и функции dy и dx .
В SciPy есть другие функции для вычисления тройных интегралов, n интегралов, интегралов Ромберга и других. О них можно узнать подробнее с помощью help .
Функции оптимизации
В scipy.optimize есть часто используемые алгоритмы оптимизации:
Функция Розенброка
Функция Розенброка ( rosen ) — это тестовая проблема для оптимизационных алгоритмов, основанных на градиентах. В SciPy она определена следующим образом:
Nelder-Mead
Это числовой метод, который часто используется для поиска минимума/максимума функции в многомерном пространстве. В следующем примере метод использован вместе с алгоритмом Нелдера — Мида.
Видео:Численное решение задачи Коши методом ЭйлераСкачать

Функции интерполяции
В сфере числового анализа интерполяция — это построение новых точек данных на основе известных. Библиотека SciPy включает подпакет scipy.interpolate, состоящий из сплайновых функций и классов, одно- и многомерных интерполяционных классов и так далее.
Одномерная интерполяция
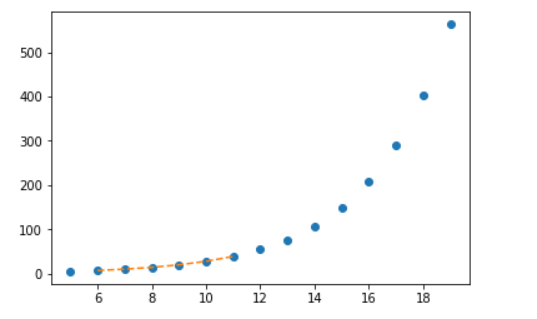
Одномерная интерполяция — это область построения кривой, которая бы полностью соответствовала набору двумерных точек данных. В SciPy есть функция interp1d , которая используется для создания одномерной интерполяции.
Вывод:
Многомерная интерполяция
Многомерная интерполяция (пространственная интерполяция) — это тип интерполяции функций, который состоит из более чем одной переменной. Следующий пример демонстрирует работу функции interp2a .
При интерполяции на двумерную сетку функция использует массивы x, y и z для приближения функции f: «z = f(x, y)» и возвращает функцию, у которой вызываемый метод использует сплайновую интерполяцию для поиска значения новых точек.
Вывод:
Видео:Решение 1 го нелинейного алгебраического уравнения в PythonСкачать

Функции преобразования Фурье
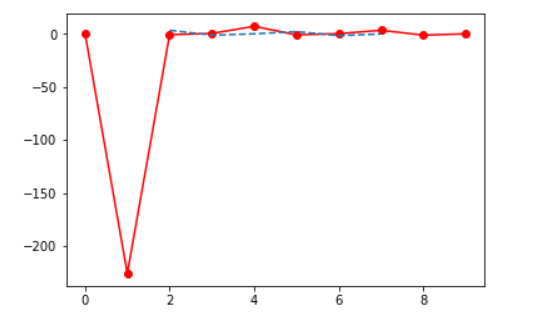
Анализ Фурье — это метод, который помогает представлять функцию в виде суммы периодических компонентов и восстанавливать сигнал из них. Функции fft используются для получения дискретной трансформации Фурье реальной или комплексной последовательности.
Похожим образом можно найти обратное значение с помощью функции ifft .
Функции обработки сигналов
Обработка сигналов — это область анализа, модификации и синтеза сигналов: звуков, изображений и т. д. SciPy предоставляет некоторые функции, с помощью которых можно проектировать, фильтровать и интерполировать одномерные и двумерные данные.
Фильтрация:
Фильтруя сигнал, можно удалить нежелаемые составляющие. Для выполнения упорядоченной фильтрации используется функция order_filter . Она выполняет операцию на массиве. Синтаксис следующий:
a — N-мерный массив с входящими данными
domain — массив масок с тем же количеством размерностей, что и у массива a
rank — неотрицательное число, которое выбирает элементы из отсортированного списка (0, 1…)
Сигналы
Подпакет scipy.signal также состоит из функций, с помощью которых можно генерировать сигналы. Одна из таких — chirp . Она является генератором частотно-модулированного сигнала, а ее синтаксис следующий:
Вывод:
Линейная алгебра
Линейная алгебра работает с линейными уравнениями и их представлениями с помощью векторных пространств и матриц. SciPy построена на базе библиотек ATLAS LAPACK и BLAS и является очень быстрой в сфере решения проблем, связанных с линейной алгеброй. В дополнение к функциям из numpy.linalg scipy.linalg также предоставляет набор продвинутых функций. Если numpy.linalg не используется вместе с ATLAS LAPACK и BLAS, то scipy.linalg работает намного быстрее.
Нахождение обратной матрицы
С математической точки зрения обратная матрица A — это матрица B, где AB = I, а I — это единичная матрица, состоящая из единиц по диагонали. Это можно обозначить как B=A-1. В SciPy такого можно добиться с помощью метода linalg.inv .
Нахождение определителей
Значение, полученное арифметическим путем из коэффициентов матрицы является определителем квадратной матрицы. В SciPy это делается с помощью функции det с таким синтаксисом:
det(a, overwrite_a=False, check_finite=True)
a — (M, M) — это квадратная матрица
overwrite_a(bool, optional) — разрешает перезаписывать данные
check_finite(bool, optional) — для проверки состоит ли матрица только из конечных чисел
Разреженные собственные значения
Разреженные собственные значения — это набор скаляров, связанных с линейными уравнениями. ARPACK предоставляет способ быстрого нахождения этих значений (собственных векторов). Вся функциональность скрыта в двух интерфейсах: scipy.sparse.linalg.eigs и scipy.sparse.linalg.eigsh .
Интерфейс eigs позволяет находить собственные значения реальных или комплексных несимметричных квадратных матриц, а eigsh содержит интерфейсы реальных симметричных или комплексных Эрмитовых матриц.
Функция eigh решает обобщенную проблему собственного значения для комплексной Эрмитовой или реально симметричной матрицы
Разреженные структуры данных и алгоритмы
Разреженные данные состоят из объектов, которые в свою очередь состоят из линий, точек, поверхностей и так далее. Пакет scipy.spatial из SciPy может вычислять диаграммы Вороного, триангуляцию и другое с помощью библиотеки Qhull. Он также включает реализации KDTree для точечных запросов ближайших соседей.
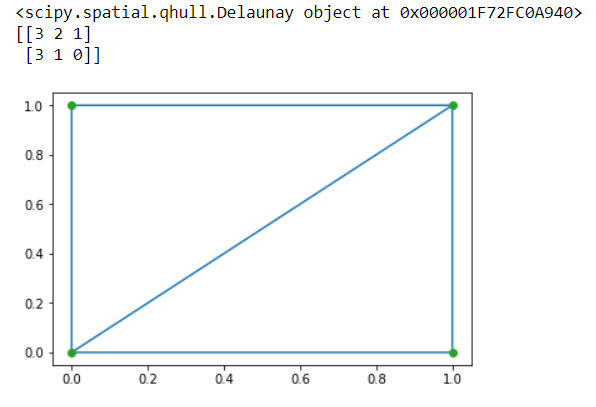
Триангуляции Делоне
С математической точки зрения триангуляции Делоне для набора дискретных точек на плоской поверхности — это триангуляция, где ни одна точка из представленных не расположена внутри описанной окружности любого треугольника.
Вывод:
Функции многомерной обработки изображений
Обработка изображений — это выполнение операций над изображением по получению информации или улучшенной копии этого изображения из оригинала. Пакет scipy.ndimage состоит из нескольких функций обработки и анализа изображений, которые нужны для работы с массивами с произвольной размерностью.
Свертка и корреляция
В SciPy есть несколько функций для свертки и корреляции изображений.
- Функция correlate1d используется для вычисления одномерной корреляции по заданной оси
- Функция correlate предлагает многомерную корреляцию для любого массива с определенным ядром
- Функция convolve1d используется для вычисления одномерной свертки вдоль заданной оси
- Функция convolve предлагает многомерную свертку для любого массива с определенным ядром
Файловый ввод/вывод
Пакет scipy.io предоставляет несколько функций, которые помогают управлять файлами в разных форматах, включая MATLAB, файлы IDL, Matrix Market и другие.
Для использования его нужно сначала импортировать: