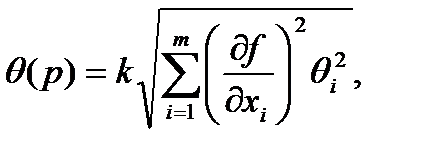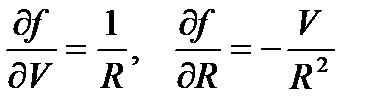Бюджет неопределенности измерения модель измерения уравнение измерения (8 видео)

Тема 8. Оценка неопределенности испытаний (стр. 1 )

Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8

Содержание

Тема 8. Оценка неопределенности испытаний.
Вопросы:
1. Оценка неопределенности методом моделирования.
Вопрос 1. Оценка неопределенности методом моделирования.
НЕОПРЕДЕЛЕННОСТЬ ИЗМЕРЕНИЙ ДЛЯ ЧАЙНИКОВ И. НАЧАЛЬНИКОВ
Методика оценивания результата измерений и его неопределенности
📺 Видео

Видео:Оценка неопределенности измеренийСкачать

Тема 8. Оценка неопределенности испытаний.

Видео:Оценка неопределенности результатов измеренийСкачать

Вопросы:

Видео:Неопределенность измерений - Uncertainty of measurementСкачать

1. Оценка неопределенности методом моделирования.

2. Источники неопределенности.

3. Эмпирический метод оценки неопределенности.

Видео:Вебинар Оценка неопределенности измерений в аккредитованных испытательных лабораториях (17.01.2023)Скачать

Вопрос 1. Оценка неопределенности методом моделирования.

В настоящее время выделяют три надежных способа (подхода) по количественной оценке неопределенности измерения:

1. Метод моделирования, изложенный в GUM, с применением закона распределения неопределенности;

2. Метод моделирования Монте-Карло (Приложения 1 к GUM);

3. Эмпирические методы, основанные на внутрилабораторном или межлабораторном исследовании выполнения методов измерений (испытаний).

Метод моделирования является наиболее разработанным и широко используемым для оценки неопределенности измерений.

Метод состоит в установлении модели измерений, которая связывает измеряемую величину с влияющими величинами, расчете стандартной неопределенности каждой влияющей величины и оценке, с учетом коэффициентов чувствительности, стандартной неопределенности измеряемой величины. При использовании этого метода предполагается, что поправки на значимые систематические эффекты включены в модель. Применение закона распространения неопределенности дает возможность оценить суммарную неопределенность, связанную с результатом. Подход зависит от частных производных для каждой влияющей величины, следовательно, зависит от вида функциональной зависимости результата или, если формой является алгоритм, от численного дифференцирования.

Типичными выходными данными подхода моделирования является «бюджет неопределенности», дающий итоговую оценку суммарной стандартной неопределенности результата измерения из неопределенностей входных величин. Бюджет неопределенности включает данные о каждой «входной величине» и ее вкладе в результат измерения и неопределенность и сами данные о результате измерения и ее неопределенности как показано ниже на схеме (рис. 3).

Бюджет неопределенности относится к определенному результату измерения. Однако, разработанный алгоритм бюджета неопределенности, обычно изложенный в методике расчета неопределенности, можно применить ко всем измерениям, проведенным с использованием того же метода. Для любого нового измерения (суммарная) стандартная неопределенность u(y) получается через введение в алгоритм входных данных xi и u(xi) для этого измерения, на основании которых затем будут получены y и u(y).

стандартная неопределенность u(xi)

(суммарная) стандартная неопределенность u(y)

коэффициент охвата k

вклад в неопределенность

расширенная неопределенность
U(y) = k·u(y)

Рис.3. Элементы бюджета неопределенности

Так как бюджет неопределенности содержит информацию об относительных величинах вкладов различных входных величин в неопределенность, то эта информация может быть использована для улучшения методики измерения и повышения ее точности.

Процесс оценивания неопределенности по методу моделирования состоит из следующих этапов.

1. Описание измерения, составление его модели и выявление источников неопределенности.

Любой процесс измерения можно представить в виде последовательности выполняемых операций. Поэтому для описания измеряемой величины и выявления источников неопределенности целесообразно представить цепь преобразования измеряемой величины в виде схемы, отображающей последовательность процесса измерений.

В большинстве случаев измеряемая величина Y не является прямо измеряемой, а зависит от N других измеряемых величин Х1, Х2 … ХN и выражается через функциональную зависимость

, (1)

Y – выходная величина.

Входные величины X1, X2, … XN, от которых зависит выходная величина Y, являются непосредственно измеряемыми величинами и сами могут зависеть от других величин, включая поправки и поправочные коэффициенты на систематические эффекты:

и т. д. (2)

Описание измеряемой величины в виде функциональной зависимости (математической модели), связывающей измеряемую величину с параметрами, от которых она зависит, называется моделированием.

Стадия моделирования является чрезвычайно важной, так как от правильности и тщательности составления модели измерения, которая определяется необходимой точностью, зависит количество источников неопределенности.

С целью обобщения источников неопределенности измеряемую (выходную) величину и выявленные источники неопределенности: входные величины и величины, на них влияющие целесообразно представить на диаграмме «причина – следствие» (рис. 4):

Рис. 4. Диаграмма «причина-следствие»

Источниками неопределенности могут быть пробоотбор, условия хранения, аппаратурные эффекты, чистота реактивов, условия измерений, влияние пробы, вычислительные и случайные эффекты, влияние оператора.

2.Оценивание значений и стандартных неопределенностей входных величин. Следующим этапом после выявления источников неопределенности является количественное описание неопределенностей, возникающих от этих источников. Это может быть сделано двумя путями:

– оцениванием неопределенности, возникающей от каждого отдельного источника с последующим суммированием составляющих;

– непосредственным определением суммарного вклада в неопределенность от некоторых или всех источников с использованием данных внутрилабораторных или межлабораторных исследований об эффективности метода в целом.

Для каждой входной величины необходимо определить оценку и стандартную неопределенность. При этом все входные величины вследствие того, что их значения не могут быть точно известны, являются случайными непрерывными. Тогда оценками входных величин (x1, x2 … xN), обозначаемыми малыми буквами, являются их математические ожидания, а стандартными неопределенностями u(xi) входных величин – стандартные отклонения. Оценку входных величин и связанную с ней стандартную неопределенность u(xi) получают из закона распределения вероятностей входной величины.

Оценивание неопределенности от каждого источника возможно двумя способами: по типу А (путем статистического анализа ряда наблюдений) и по типу В (иным способом, чем статистический анализ ряда наблюдений).

Исходными данными для оценивания стандартной неопределенности по типу А являются результаты многократных измерений xi1, … xim; i=1, …, m. На основании полученных результатов рассчитывается среднее арифметическое по формуле (49), которое является оценкой входной величины Xi:

. (3)

Стандартная неопределенность, связанная с оценкой является экспериментальным стандартным отклонением среднего значения и равна положительному квадратному корню из экспериментальной дисперсии среднего значения.

Стандартная неопределенность u(xi) вычисляется по формуле:

(4)

для результата измерения , вычисленного как среднее арифметическое.

Исходными данными для оценивания стандартной неопределенности по типу В является следующая априорная информация:

– данные предшествовавших измерений величин, входящих в уравнение измерения;

– сведения о виде распределения вероятностей;

– данные, основанные на опыте исследователя или общих знаниях о поведении и свойствах соответствующих средств измерений и материалов;

– неопределенности констант и справочных данных;

– данные поверки, калибровки, сведения изготовителя о средстве измерения и др.

Если оценка xi берется из спецификации изготовителя, свидетельства о поверке, справочника или другого источника, то неопределенность обычно дается как интервал ±a отклонения входной величины от ее оценки. Имеющуюся информацию о величинах xi необходимо правильно описать с помощью функции распределения вероятностей. Для определения стандартной неопределенности входных величин необходимо воспользоваться законом распределения вероятностей xi. При этом чаще всего используют следующие основные законы распределения:

Формулы и способы применения представлены в таблице 2.

Формулы расчета стандартной неопределенности

Видео:Неопределенность измерения и интерпретация результатов исследований пациентов.Скачать

НЕОПРЕДЕЛЕННОСТЬ ИЗМЕРЕНИЙ ДЛЯ ЧАЙНИКОВ И. НАЧАЛЬНИКОВ

Анфиса Сабурова 3 лет назад Просмотров:

1 И. П. Захаров НЕОПРЕДЕЛЕННОСТЬ ИЗМЕРЕНИЙ ДЛЯ ЧАЙНИКОВ И. НАЧАЛЬНИКОВ Учебное пособие Харьков 2013

2 Навчалъне видання ЗАХАРОВ 1гор Петрович НЕВИЗНАЧЕШСТЬ ВИМ1РЮВАНБ ДЛЯ ЧАЙНИК1В I. КЕР1ВНИК1В Навчальний поабник Формат 60 х90><6. У м о в. друк. арк. 2,25. Тираж 100 прим. Зам. 235 Друк ФОП Васильева Н. В , м. Харюв, просп. Лешна, 14 Тел. (057)

3 УДК ББКЗО.ЮЦ 3 38 Захаров И. П Неопределенность измерений для чайников и. начальников: учеб. пособ. / И. П. Захаров, X. : с. В учебном пособии в популярной форме изложены основные вопросы оценивания неопределенности измерений. Рассматривается базовый алгоритм оценивания неопределенности, особенности учета законов распределения входных величин при вычислении коэффициента охвата, составление бюджета неопределенности, учет наблюдаемой корреляции, взаимный пересчет погрешностей и неопределенностей измерений. Изложение материала сопровождается простыми примерами. В приложении приведены справочные материалы и поясняющие иллюстрации Рекомендуется широкому кругу читателей всех возрастных категорий и уровней математической подготовки для быстрого погружения в тему. УДК ББК 30.10Ц Захаров И. П., 2013

4 «Нет ничего боже противоречащего складу ума, памяти и соображению, чем то, что предлагают эта ученые. Абстракциям и пустым надеждам принесено в жертву благо теперешних поколений, ибо чтобы заставить старую нацию принять новые единицы необходимо переделать все административные правила, все расчеты промышленности. Такая работа устрашает разум». Наполеон о метрической системе.

5 ПРЕДИСЛОВИЕ Понятие «неопределенность» прочно вошло в жизнь современных метрологов как продукт неизбежного процесса международной стандартизации оценивания качества измерений. Концепция неопределенности болезненно вытесняет привычную, узаконенную в многочисленных отечественных нормативных документах теорию погрешности (см. эпиграф). Внедрение этой концепции требует проведения соответствующей методической работы. В году автором этой книги было издано учебное пособие [1 ], рассчитанное на студентов метрологических специальностей вузов. Настоящее пособие предназначено для тех, кто, занимаясь метрологией, не обладает достаточной базой в области математической статистики, однако, в силу сложившихся жизненных обстоятельств, вынужден в сжатые сроки разобраться в основных принципах оценивания неопределенности измерений. Таковыми являются либо не учившие, либо подзабывшие, по роду деятельности много лет не применявшие полученные знания на практике. С пониманием относясь к обеим категориям, автор предлагает им доступный и краткий вариант изложения основ неопределенности измерений. Этот вариант отработан на многочисленных курсах повышения квалификации и семинарах, проведенных автором для аудиторий с широким спектром начальной подготовки. При изложении материала автор руководствовался известным изречением Галилея: «Нельзя чему-нибудь обучить человека, можно только помочь ему обнаружить это внутри себя». Поэтому текст пособия сопровождается простыми примерами, известными на бытовом уровне, множеством иллюстраций и заданий для самоподготовки. Для сохранения ясности изложения, многие уточняющие подробности помещены в сноски и вынесены в приложения. В конце пособия приведен список нормативной и научнометодической литературы, способствующий при необходимости более подробному изучению данного материала. Автор заранее выражает благодарность всем читателям, которые будут присылать свои отзывы и замечания по адресу: 4

6 1. Что такое неопределенность измерений? Неопределенность измерений — это характеристика недостоверности измерений, принятая на международном уровне1. Понятие «неопределенность» произошло от английского слова «uncertainty»2. Неопределенность отражает отсутствие точного знания (истинного) значения измеряемой величины Y и выражает сомнение в том, насколько точно результат измерения у представляет Y. В соответствии с определением [2], неопределенность — это параметр, связанный с результатом измерений у и характеризующий разброс значений, которые можно обоснованно приписать измеряемой величине Y. Первая буква слова «uncertainty» U стала обозначением этого параметра. Приведенное определение лучше всего иллюстрируется стандартной формой записи результата измерения: У = у ±U, р = 0,95. (1) Из выражения видно, что вероятный разброс значений Y находится в диапазоне ±U относительно результата измерения у (рис. 1 ), а степень обоснованности нахождения значений Y в этом интервале определяется вероятностью(уровнем доверия) р = 0,95. 2 U — ] I > у U у y+u Y Рис. 1. К определению неопределенности измерения 1 Руководство по выражению неопределенности измерений (GUM) [2] разрабатывали 7 ведущих международных организаций: Международное Бюро Мер и Весов (BIPM), Международная Организация по Стандартизации (ISO), Международная Организация по Законодательной Метрологии (OILM), Между народная Электротехническая Комиссия (ШС), Международный Союз Чистой и Прикладной Физики (IUPAP), Между народный Союз Чистой и Прикладной Химии (IUPAC), Международная Федерация Клинической Химии (IFCC). 2 UncertaintyB переводе означает неопределенность, недостоверность, неуверенность. неясность, неизвестность, сомнительность, изменчивость. 5

7 2. Основные принципы оценивания неопределенности измерений В данном пособии будет рассмотрен так называемый модельный подход к оцениванию неопределенности измерений. Суть его заключается в использовании модельного уравнения Y = f(x h X 2. Xm), (2) связывающего между собой входные величины Х,Х2,- -,Хт измерительного процесса с измеряемой (выходной) величиной Y 3 (рис. 2). При этом по неопределенностям, связанным с входными величинами, вычисляют неопределенность измеряемой величины, поэтому модельный подход часто называют восходящим. Xi х2 хт Измерительный процесс Y Рис. 2. Иллюстрация модельного подхода В основуреализации модельного подхода положены пять основных принципов, приведенных в Рекомендациях INC-1 (1980) рабочей группы по оцениванию неопределенности. В адаптированном к тексту выпущенного значительно позднее (1992) Руководства по выражению неопределенности измерений (GUM) [2] изложении их можно представить следующим образом: 1) Все составляющие неопределенности входных величин можно сгруппировать в две категории в соответствии со способом их оценивания 3 Примером модельного уравнения может служить рассмотренное далее (п,4.1) выражение, связывающее между собой скорость транспортного средства (V) с длиной пройденного пути (L) и времени его прохождения (7). 4 ГЗ отличие от теории погрешностей, где основным классификационным признаком является характер изменчивости составляющих (систематическая и случайная), в концепции неопределенности основным классификационным признаком является способ оценивания составляющих неопределенности (по типу А и В). 8 категория А — составляющие, оцениваемые путем применения статистических методов (путем обработки результатов многократных измерений); категория В — составляющие, оцениваемые другим способом (по характеристикам, взятым из паспорта на прибор, методик выполнения измерений, из предыдущих экспериментов, из справочников и т. д.). 2) Составляющие типа А оцениваются как стандартные неопределенности (и д ), равные средне квадратическим отклонениям (СКО) средних арифметических многократных наблюдений. Эти составляющие характеризуются тагами степеней свободы v j = п — 1, где п — число наблюдений. 3) Составляющие типа В («g) оцениваются как стандартные (среднеквадратические) отклонения, получаемые из известных границ, в которых могут находиться значения измеряемых величин. Эти составляющие характеризуются числами степеней свободы Vft =оо5. 4) Все составляющие формируют суммарную стандартную неопределенностьис, которая вычисляется по правилу суммирования дисперсий6: (3) откуда путем извлечения корня из обеих частей равенства, получаем выражение, называемое законом распространения неопределенности. Суммарная стандартная неопределенность характеризуются эффективным числом степеней свободы v ej j, которое определяется соотношением составляющих и д. ид и числами их степеней С вободы V J И Vft. (4) 5 Предполагается, что для нахождения границ измеряемых величин было проделано бесконечное количество наблюдений. 6 Дисперсия равна квадрату стандартной неопределенности. Правило суммирования дисперсий: дисперсия суммы нескольких независимых величин равна сумме их дисперсий. 7

9 5) Интервальной оценкой неопределенности является расширенная неопределенность U, которую получают путем умножения стандартной суммарной неопределенности ис на коэффициент охвата : U -к-ис. (5) В общем случае коэффициент охвата находят как коэффициент Стьюдента1 (см. Приложение 1) для вероятности 0,95 и эффективного числа степеней свободы >ej j : k = t0,95 (veff)- (6) В пределе, при е& ->оо, к =2. 3. Источники неопределенности измерений Источниками неопределенности измерений являются: наблюдаемое рассеивание показаний используемых при измерении средств измерительной техники (СИТ) (обусловливающие стандартные неопределенности типа А) и поправки на не исключенные систематические погрешности (НСП) СИТ (обусловливающие стандартные неопределенности типа В). Кроме того, источниками неопределенности типа В может являться недостоверность используемых справочных данных, округление результатов измерения или применяемых констант Наблюдаемое рассеивание показаний Если при п — кратном измерении одного и того же значения измеряемой величины показания СИТ х,х 2. хпхаотически отличаются друг от друга (имеют разброс), то их можно рассматривать как реализации случайной величины. Наиболее полной характеристикой любой случайной величины является ее закон распределения. Экспериментально закон распределения можно построить в 7 Стьюдент — псевдоним английского ученого-статистика Уильяма Госсета, работавшего на пивоваренной фабрике Гиннесс и занимавшегося оценкой качества пива и урожайности ячменя по малым выборкам. 8

10 виде гистограммы (столбиковой диаграммы) при наличии большого числа показаний СИТ ( и > 40) (рис. 3). Рис. 3. Гистограмма распределения показаний СИ Г Высота каждого столбика равна количеству показаний СИТ, попавших на интервал его существования шириной = (хтах — х;пш)/l. Количество интервалов L зависит от числа измерений «8. Принято считать, что закон распределения случайных погрешностей — нормальный (гауссов) (рис. 4)9. 8 В рекомендациях ВНИИМ [3] предлагают выбирать 7 9 интервалов при числе измерений ; 8 12 интервалов при числе измерений ; интервалов при числе измерений и интервала при числе измерений Этот закон описан математически немецким математиком К.Ф. Гауссом в сочинении «Теория движения небесных тел» (1809). Центральная предельная теорема теории вероятности показывает, что в случае, когда результат измерения складывается под действием многих независимых причин, причем каждая из них вносит лишь малый вклад, а совокупный итог определяется путем сложения, то распределение результата измерения близко к нормальному. Считается, что получить нормальный закон можно уже при суммировании более четырех равнозначных составляющих, распределенных по любому другому закону. Сумма составляющих, распределенных нормально, также имеет нормальный закон распределения. 9

11 Рис. 4. Плотность распределения вероятности для нормального закона Характеристикой положения такого закона распределения является среднее арифметическое х отдельных показаний СИТ, принимаемое за.результат измерения. _ = xl +x2 +. +x m ] _ ^ Xi (?) п Ы ПРИМЕР Показания весов при трехкратном взвешивания массы тела человека составили 81 кг, 79 кг и 80 кг. Среднее арифметическое значение этих показаний равно. _ ОЛ т = = 80 кг. Отклонение отдельных показаний СИТ Х,Х2,—,хп от среднего ю значения х описывается характеристикой, называемой дисперсия : (хл- х ) 2 + ( х т — х ) (х — х ) 2 1 Д / 2 D(x) = i — i —- L ^ =—— ( x i — x ) (8 ) п — 1 п — 1

ПРИМЕР. Для приведенных выше показаний весов дисперсия отдельных показаний составит: (81»»)’ (J1 (»»- *» ) . кг, От английского слова dispersion — разброс, рассеивание. 1 0

12 Из рассмотренного примера видно, что размерность результата измерения (кг) отлична от размерности дисперсии (кг2). Для согласования этих размерностей из значения дисперсии извлекается корень и получается СКО отдельных показаний: S(x) = jd(x) = — 1 _ ( х/-х)2. (9) 4=1 ПРИМЕР, Для приведенных выше показаний весов СКО отдельных показаний составит: S(m) = (81-80)2 + (79-80)2 + (80-80)2 I кг. 3-1 Поскольку за результат многократного измерения принимают среднее арифметическое отдельных показаний СИТ, то характеристикой разброса х служит не СКО отдельных показаний S(x), а СКО средних арифметических этих показаний S(x), называемая стандартной (среднеквадратической) неопределенностью типа А( ид), которая оказывается в yfn раз меньше S(x): ид(х)= 7^ = J — У ‘(xj-x)2. (10) Этой неопределенности приписывают число степеней свободы va = n — 1. ПРИМЕР. Для приведенных выше показаний весов стандартная неопределенность типа4 составит: M W — i ( 8 1

8 0 )2 + ( ) 2 4 (8 0

8 0 ) 2-0.^ K r. А У 3(3-1) Этой стандартной неопределенности приписывают число степеней свободы v j (т) = 3-1 = 2. 11

13 3.2. Характеристики НСП Систематическая погрешность — это погрешность, которая остается постоянной или закономерно изменяется при повторных измерениях величины Y. Такая особенность систематической погрешности позволяет оценить ее значение (в результате проведения калибровки) и внести поправку в результат измерения. Поскольку значение поправки определяется неточно, в исправленном результате измерения будет присутствовать неисключенная систематическая погрешность (НСП) А нсп >Для которой известны границы ± 0 интервала, в котором ее неизвестное значение может находиться с равной вероятностью. Поэтому НСП СИТ приписывают равновероятный (равномерный) закон распределения НСП, плотность вероятности которого ( >й?/)изображена на рис. 5. pdji АцСи) А АНсп Рис. 5. Равномерный закон распределения НСП Для такого закона распределения11 СКО НСП (неопределенность типа В) равна: Для поверенных СИТ оценивание неопределенности типа В производится в соответствии с табл. 1. В таблице применены известные формулы, связывающие границы относительной S и приведенных у и X погрешностей, через которые выражается класс точности средства измерения [4], страницами абсолютной погрешности 0 в предположении равномерного распределения НСП внутри грашщ. 11 Коэффициенты для других встречающихся на практике законов распределения приведены в п.п

14 Таблица 1. Формулы для расчета стандартной неопределенности типа В Пример обозначения класса точности Вид и обозначение нормируемой погрешности Формула для расчета стандартной неопределенности типа В Рис. 6 1, 0 Рис. 7 Рис. 7 2,0 /0 Д Рис. 8 Относительная, 8 Приведенная, у Приведенная к длине неравномерной шкалы. X Относительная,^ (^ср+ ^изм ) ив = Х (14) х ср7з-ю о% (12) Г ( X И Г ив — c+d л н 1 г- шм (15) » L. И ю м JJ л/3 *1 0 0 % В таблице использованы обозначения: Х изм — измеренное значение (показание СИТ), Х н — нормированное значение измеряемой величины (чаще всего — предел измерения); Х ср — значение измеряемой величины, соответствующее геометрической средине существенно неравномерной шкалы. Рис. 6. Шкала омметра класса точности(1д 13

15 ПРИМЕР. Необходимо оценить стандартную неопределенность типав измерения сопротивления омметром М3 71 (рис. 6 ). Показания прибора 5 Ом. Класс точности прибора(к5). Воспользовавшись формулой (1 2 ) табл. 1, получаем: ив =5 — А» * — 15 % J = 0,043 Ом. л/з-100% 7з-100% 1. Рис. 7. Классы точности мегомметра Е6-17: в диапазоне ОД. 0,3 ко м- 2,5Д ком -1,5;.300 МОм — ^ 5 ; МОм до МОм ПРИМЕР: Оценить стандартную неопределенность типа В измерения сопротивления на пределе 100 ком мегомметром Е6-17 (рис. 7). На указанном пределе класс точности прибора 1,5. Воспользовавшись формулой (13)табл. 1, получаем: Хтт, _п/ ЮОкОм л л пи = у р = 1,5% 7= = 0,87к0м. 7 з % V % Следует отметить, что при таком представлении класса точности неопределенность типа В не зависит от значения измеряемой величины. 14

16 ПРИМЕР. Необходимо оценить стандартную неопределенность типа В измерения сопротивления на пределе 10 МОм мегомметром Е6-17 (рис. 7). На указанном пределе класс точности прибора 2,5, Геометрическая середина шкалы на этом пределе составляет 20 jviom. Показания прибора 36 МОм. Воспользовавшись формулой (14) табл. 1, получаем: (Хср +Х И З М ) 2 (20МОм + 36МОм)2 Л ие = Х± = 2,5% =г = 2,ЗМОм. Хсрл/3-100% 20 МОм л/3 100 % Рис. 8. Магазин сопротивлений класса точности 0,02/2-10 ‘ ПРИМЕР. Необходимо оценить стандартною неопределенность типа В воспроизведения сопротивления магазином Р4831 (рис. 8 ). Установленное значение сопротивления на магазине 79,6 ком. Нормированное значение сопротивления составляет Ом, Класс точности магазина 0,02/2-10’6. Воспользовавшись формулой (15) табл. 1, получаем: ив = c+d шм — 1 а; IBM л/3-100% 0, гб л/3-100 =9.2 Ш. 15

17 Для калиброванных СИТ стандартная неопределенность рассчитывается из данных о расширенной неопределенности U и коэффициенте охвата к, взятых из сертификата о калибровке по формуле: U ив=

г- к ПРИМЕР: Оценить стандартную неопределенность типа В воспроизведения сопротивления катушкой Р321. В сертификате о калибровке указано, что значению сопротивления приписана расширенная неопределенность 1 мом с коэффициентом охвата к = 2 для уровня доверия р = 0,95. Используя формулу (16) получаем стандартную неопределенность типа В. 1 мом ив = — = 0,5м0м. 4. Базовый алгоритм оценивания неопределенности измерений Этот алгоритм описан в GUM [1] и включает в себя следующие операции Составление модельного уравнения Модельное уравнение (2) выражает зависимость между выходной (измеряемой) величиной Yи входными величинами^,х2, Хт: Y = f(x l. xj ПРИМЕР. Определение скорости V транспортного средства, проходящего расстояние /.за время Т: 4.2. Оценивание входных величин Значения входных величин находят путем их измерения с одно-

18 кратными или многократными наблюдениями или берут из внешних источников. При проведении многократных измерений за значение входной величины принимают среднее арифметическое результатов ряда отдельных наблюдений (7): 1 » x = — t x f » f t ПРИМЕР. Путь, проходимый транспортным средством /=1000 м известен априори. Время прохождения этого отрезка пути измерялось 3-х кратно секу ндомером, при этом были получены следующие результаты. = 1 0 0, 1 с; f2 =99,9 с; t3 = 1 0 0, 0 с. Среднее значение этих измерений равно: _ 100,1 + 99, ,0 1ЛЛ t = = с Вычисление оценки результата измерения Оценку выходной величины у получают при подстановке в модельное уравнение оценок входных величинх. хт : y = f(xh. xm).(17) ПРИМЕР. Скорость транспортного средства будет равна: м 1П, v = = 1 0 м/с с 4.4. Вычисление стандартных неопределенностей входных величин Стандартная неопределенность измерения типа A i-й входной величины х, находится по формуле: 17

19 I «4 (*,)=’ (18) где n t — количество наблюдений, выполняемых при измерении xt. ПРИМЕР. Стандартная неопределенность типа А оценки времени прохождения отрезка пути L транспортным средством будет равна: и (Т)= 1( т 1

100)2 +( » 9-100)2 +(100-Ю 0 ) 2 _ ОЛ _ 0 05S V 3(3-1) 7з Стандартная неопределенность типа lit-и входной величины находится в зависимости от априорной информации о изменчивости входной величины. Если /-я входная величина является неисключенной систематической погрешностью (НСП) с границами ±0 то ее неопределенность вычисляется по формуле: М х/) = 0,/а > где а, — коэффициент, соответствующий принимаемому закону распределения внутри границ НСП: для равномерного (или неизвестного) закона распределения а = л/3; для нормального закона распределения (для вероятности р=0,95)а=2; для треугольного закона распределения а = -ч/б; для закона арксинуса а = л/2 ; ПРИМЕР. Стандартная неопределенность типа В оценки времени прохождения отрезка пути L транспортным средством будет вычисляться из границ НСП секундомера 0(=О,1 с, откудаub(t)-о A j-j3 =0.058с. Стандартная неопределенность типа В оценки отрезка пути L транспортным средством будет вычисляться из границ НСП задания L: 0t=l м, откудаив(/) = l/л/з = 0,58 м. 18

20 4.5. Вычисление вклада неопределенности входной величины в неопределенность измеряемой величины Вклад неопределенности каждой входной величины в неопределенность измеряемой величины (суммарную стандартную неопределенность) ut (у) определяют как произведение неопределенности входной величины и(х,) на коэффициент чувствительности с,: Щ(у) = сги(х1). (19) Коэффициенты чувствительности с, показывают, как оценка выходной величины убудет изменяется с изменением оценок входных величин х,. Их находят как частные производные выходной величины по каждой из входной величин12: ду dy (20)

дх.. Таблица частных производных и правила дифференцирования приведены в Приложении 3. ПРИМЕР. Коэффициент чувствительности скорости транспортного средства к изменению пройденного пути будет равен: _dv_dv J_ = 0, 0 1 с» С’

t? = с Коэффициент чу вствительности скорости транспортного средства к изменению времени будет равен: _dv_dv L_ dt

Г2 Ю0 0 А 1 / 2-0, 1 м/с. / = м,* = с След овательно, вклад неопределенности задания пути в неопределенность измерения скорости равен: ut(v) = CjUB(1) = 0,01 с- 1 0,58 м = 0,0058 м /с. Вклад неопределенности измерения времени типа А в неопределенность измерения скорости равен: 12 Графическая иллюстрация коэффициента чувствительности приведена в приложении 2. 19

21 UiA (y) = c,ua( t ) = -0,1 м/с 2-0,058 с = 0,0058 м/с Вклад неопределенности измерения времени типа В в неопределенность измерения скорости равен: ии (у) = c,ub(t) = -0,1 м/с 2-0,058 с = 0,0058 м/с Для модельного уравнения в виде линейной комбинации входных величин вида У=а1Хj + а2х атхт, где а, а2. ат — постоянные коэффициенты, коэффициенты чувствительности равны коэффициентам при входных величинах: С aic2

ат. > ат Для модельного уравнения в виде произведения или частного от деления входных величин, например: у _ модули коэффициентов чувствительности равны модулям отношения значения измеряемой величины у к значению соответствующей входной величины: У_, ы = У > ы = У_ * 1 х2 х3 ПРИМЕР. Модуль коэффициента чувствительности скорости транспортного средства к изменению пройденного пути будет равен: 1 0 м/с — = 0, 0 1 с-1, м что совпадает со значением коэффициента чувствительности, полученным выше путем дифференцирования. Модуль коэффициента чувствительности скорости транспортного средства к изменению времени будет равен. V 1 0 м/с. /2 с, = _ = = 0, 1 м/с, 1 ( t с что совпадает со значением коэффициента чувствительности, полученным выше путем дифференцирования. 20

22 4.6. Определение стандартной неопределенности выходной величины (суммарной стандартной неопределенности) Определение суммарной стандартной неопределенности осуществляется по формулам, называемым законом распространения неопределенности. При отсутствии корреляций между входными величинами стандартная неопределенность выходной величины определяется как и ЛУ)= у-(у)=у]су(х1) + с;и2(х2) с2ти2(хт).(21) ПРИМЕР: Суммарная стандартная неопределенность измерения скорости транспортного средства будет равна: ue(v) = д/0, , ,00582 = 0,0058 7з = 0,01м/с Вычисление коэффициента охвата Коэффициент охвата представляет собой множитель, на который умножают стандартную суммарную оценку неопределенности для получения расширенной неопределенности. Его приближенное значение для уровня доверия 0,95 равно 2. При наличии вкладов неопределенности типа A, GUM рекомендует брать в качестве коэффициента охвата коэффициент Стьюдента для уровня доверия 0,95 и эффективного числа степеней свободы ‘ф определяемого по формуле Велча-Саттерсвейта [1 ]: Для прямых многократных измерений (или для косвенных многократных измерений с одной входной величиной, измеряемой по типу А) с числом наблюдений п эта формула может быть представлена в виде: (23) 21

23 ПРИМЕР: Эффективное число степеней свободы при измерении скорости транспортного средства будет равно: ОД = 2-(л/3) 4 = Тогда коэффициент охвата будет вычисляться как коэффициент Стьюдента для уровня доверия 0,95 и эффективного числа степеней свободы 18: к = ^0,95 (Уeff ) = 2 Д При отсутствии вкладов неопределенности типа А формула (22) дает бесконечность, поэтом> коэффициент охвата формально должен быть равен коэффициенту Стьюдента от бесконечности для вероятности 0,95, т.е. к = * 0 9 5(0 0 ) = 2,0,Однако такое значение коэффициента охвата соответствует случаю, когда значениям измеряемой величины Y приписывают нормальный закон распределения (рис. 4 ), являющийся результатом влияния на нее большого числа факторов (источников неопределенности). Нормальный закон для вероятности 100 % имеет бесконечные границы. Для ограничения интервала возможных значений Y при указании расширенной неопределенности используют вероятность (уровень доверия) /? = 0,95. Если среди вкладов неопределенности имеется доминирующий (отличающийся не менее чем в 3 раза от остальных), распределенный по равномерному закону, закон распределения выходной величины уже нельзя считать нормальным. В этом случае коэффициент охвата можно взять из табл. 2 [5]. Таблица 2. Значения коэффициентов охвата для заданного соотношения двух доминирующих равномерно распределенных вкладов неопределенности типа В, ubllub 0-0, 1 0, 2 о,з 0,4 0,5 0, 6 0,7 0, 8 0,9- к 1,65 1,70 1,75 1, 8 1,83 1, 8 6 1, 8 8 1,89 1,90 В табл. 2 ug и и%2 — соответственно значения наибольшего и второго по величине вкладов неопределенности типа В

24 4.8. Вычисление расширенной неопределенности Расширенную неопределенность U получают путем умножения неопределенности выходной величины (суммарной стандартной неопределенности) на коэффициент охвата (5): U(y) = k-uc(y). ПРИМЕР. Расширенная неопределенность измерения скорости транспортного средства будет равна: U(v) = 2,1-0,01 = 0,021м/с Запись полного результата измерения Полный результат измерения включает в себя оценку выходной величины и приписанное ей значение расширенной неопределенности с указанием уровня доверия ( 1 ): Y = y±u,p = 0,95. Значение расширенной неопределенности указывается с числом значащих цифр, не больше двух. Результат измерения, как и значения входных величин, округляют так, чтобы они соответствовали своим неопределенностям. ПРИМЕР. д Результат измерения скорости транспортного средства будет записан в виде: V = (10,00±0,21)м/с, р = 0, Составление бюджета неопределенности Полу ченные в процессе реализации базового алгоритма промежуточные результаты удобно представлять в виде бюджета неопределенности (табл. 3), который включает в себя список всех входных величин, их оценок вместе с приписанными им стандартными неопределенностями измерения, коэффициентами чувствительности и числами степеней свободы. Кроме информации о входных величинах в бюджет удобно включать информацию об измеряемой величине: результат измерения, суммарную стандартную неопределенность, эффективное число степеней свободы, коэффициент охвата и расширенную неопределенность. 23

25 Входная величина Таблица 3. Бюджет неопределенности Оценка входной величины Число степеней свободы Стандартная неопределенность Коэффициент чувствительности Вклад неопределенности Xi Ч М(Х]) V 1 С’1 Ч ОО * 2 х2 и(х2) v 2 с2 и2 (У) Хщ хт и(хт) vm ст ит (У) Расширенная Суммарная Эффективное число Измеряематат изциент неопре Резуль Коэффи стандартная неопределенность свободы степеней величина мерения охвата делен ность Y У и(у) Veff к и ПРИМЕР. Бюджет неопределенности измерения скорости (табл. 4). Таблица 4. Бюджет неопределенности измерения скорости Оценка входной величины Число степеней свободы Входная величина Стандартная неопределенность Коэффициент чувствительности Вклад неопределенности, м/с L м 0,58 м оо 0, 0 1 с4 0, с 2-0,0058 Т с — 0, 1 м/с2 0,58 с оо -0,0058 Суммарная стан Эффективное Коэффи Расширенная Измеряемадартная Результат измерения степеней охвата ность число циент неопреден- величина делелен- неопресвободы ность V 1 0 м/с 0, 0 1 м/с 18 2, 1 0, м/с 24 L

26 5. Учет корреляции при оценивании неопределенности входных величин Результаты измерения входных величины могут быть попарно коррелированны (статистически зависимы). Степень их корреляции выражается с помощью коэффициента корреляции г, значение которого лежит в пределах от -1 до 1. При г=0 корреляция отсутствует1. Корреляция возникает при одновременном наблюдении обеих входных величин в одном измерительном эксперименте (наблюдаемая корреляция). В этом случае коэффициент корреляции вычисляется по типу А по форму7ле: ] гг2 А -*,)(** -*») (23) и(х<)и<хк) 5.1. Расчет суммарной стандартной неопределенности для коррелированных данных А ' -3 Если в модельном уравнении Y = f(x h X 2. Xm) присутствуют две входных величины (например, Xj,Xj), результаты многократных измерений которых выполнены одновременно и коррелируют между собой с коэффициентом корреляции rv, то выражение для суммарной стандартной неопределенности будет иметь следующий вид: и<у) = J J c a ( v ) + Ir^cfjuix^uixj). (24) 5 3 Графическая иллюстрация наличия корреляции приведена в приложении 2. ' 25

27 ПРИМЕР. При неодновременном трехкратном измерении массы двух человек ту и т2 были получены внесенные в табл. 5 результаты измерений: Таблица 5. Результаты измерения масс mi 61 кг 60 кг 59 кг m2i 80 кг 81 кг 79 г Эти результаты по постановке задачи не должны быть коррелированы14, однако их обработка дала следующие результаты: средние значения масс: щ =60 кг, т2 =80 кг; стандартные неопределенности типа А измерения масс: ид(щ) -0,58 кг, ид(т2) =0,58 кг; коэффициент корреляции между результатами измерения масс: [(61-60X80-80) + (60-60)(81-80) + (59-60)(79-80)] г — Ы =0,5. 2 0,58-0,58 При учете корреляции стандартная неопределенность суммарной массы двух человек будет равна: и (у) = л/о,582 ч- 0, ,5-0,58-0,58 = 1кг Проверка значимости коэффициента корреляции вычисленного по ограниченному количеству наблюдений Проверить значимость коэффициента корреляции для его дальнейшего учета (или неучета) позволяет применение критерия Стьюдента): 1 4 Следует отметить, что любые перестановки результатов измерений в табл. 5 всегда будут давать коэффициент корреляции отличный от 0. Его значения будут равны: -0,5; -1; 0,5; 1. 26

28 — Д = 7 ^ 2 >Г?( и — 2 ), (26) 4 i-r 2 где t (и — 2) — коэффициент Стьюдента для числа степеней свободы (и — 2 ). ПРИМЕР. Оценим значимость коэффициента корреляции при одновременном многократном измерении массы двух человек: лд^2 = 0,5 8 t0 9 5 (3-2 ) = 12,7. л/1-0,5 2 При отсутствии корреляции стандартная неопределенность суммарной массы двух человек будет равна: w(m) = s]o,5&2+0,5&2 = 0,82 кг. Таким образом, учет несуществующей корреляции увеличивает стандартную суммарную неопределенность на 2 2 %. 6 Взаимный пересчет характеристик погрешности и неопределенности измерений 6.1. Пересчет от характеристик погрешности к оценкам неопределенности измерений Пересчет от характеристик погрешности к оценкам неопределенности измерений приведен в [6 ]. Исходными данными для расчета неопределенности являются — оценка СКО S результата измерения15; — оценка НСП в виде границ 0(/>) для заданной доверительной вероятности р ; — число составляющих НСП т. — количество результатов наблюдений п, взятых для вычисления среднего арифметического в качестве оценки результата измерения. А ЪВ качестве результата измерения принимается среднее арифметическое результатов многократных наблюдений измеряемой величины. 27

29 Используя эти исходные данные, получаем: — оценку стандартной неопределенности по типу А ид = S ; — оценку стандартной неопределенности по типу В 9 (р) в к(ру1ъ где коэффициент К(р) = 1,1 для р = 0,95; К(р) = ,А для р = 0,99 и т > оценку суммарной неопределенности ис = [^2 + iig ^2 ; — оценку эффективного числа степеней свободы 1+- иа — оценку коэффициента охвата к как коэффициента Стьюдента?о 95^ eff) Для вероятности 0,95 и полученной оценки числа степеней свободы ej j ; — оценку расширенной неопределенности Up = кйс. XI п 6.2. Пересчет от неопределенности к характеристикам погрешности измерений Пересчет от неопределенности к характеристикам погрешности измерений приведен в [ 1 ]. Исходными данными при представлении неопределенности для расчета оценок характеристик погрешности являются: — расширенная неопределенность U ; — коэффициент охвата к ; — количество результатов наблюдений п. В этом случае можно получить: 1 6 При невыполнении этого неравенства следует находить коэффициент К(р) в результате деления доверительного коэффициента, полученного из композиции равно вероятных законов распределения составляющих НСП на V3 [1 ]. 28

30 — оценку СКО, характеризующего суммарную погрешность о ‘ UP s ^ =

= uc ; — оценку СКО случайной погрешности результата измерений S — u A =S 4 /(и -1 )/у ^ 17; — оценку СКО, характеризующего НСП в=ив =у1-2 ; — оценку доверительных границ НСП 0(р) — Кр, где коэффициент К(р) = 1,1 для р = 0,95; К(р) = 1,4 для р = 0,99 и т > 4. — оценку доверительных границ погрешности tp (n-l)s + b(p) Ап = оу, р S + Sq где tр(п

) — коэффициент Стьюдента для заданной вероятности р и числа степеней свободы (п — 1). 1 Значение vejj находят из таблицы Стьюдента для известного коэффициента охвата к = %, 9 5 (veff)

31 ПРИЛОЖЕНИЕ 1 Коэффициенты Стьюдента для вероятностей 0,95 и заданного числа степеней свободы v 1!> V ‘0,95 V ‘0,95 V ‘0,95 V ‘0,95 V ‘0,95 V ‘0,95 1,0 12,7 2,0 4,30 3,0 3,18 9,0 2, , ,04 1Д 10,3 2,1 4,11 3,5 2, , , ,04 1,2 8,65 2,2 3,95 4,0 2,78 И 2, , ,03 1,3 7,50 2,3 3,81 4,5 2, , , , 0 2 1,4 6, 6 6 2,4 3,68 5,0 2, , , , 0 1 1,5 6, 0 2 2,5 3,56 5,5 2, , , , 0 0 1,6 5,52 2,6 3,48 6,0 2, , , ,99 1,7 5,12 2,7 3,39 6,5 2, , , ,98 1,8 4,80 2,8 3,32 7,0 2, , , ,97 1,9 4,53 2,9 3,25 8,0 2, , ,05 оо 1,96 ПРИЛОЖЕНИЕ 2 Графическая иллюстрация коэффициентов чувствительности У 18 Значения коэффициентов Стьюдента для дробных степеней свободы получены в работе [6 ]. 30

32 ПРИЛОЖЕНИЕ 3 Таблица производных Функция /(х) 1 Производная / (x) С (константа) 0 X 1 X2 2 x хп л/х 1 X sin(x) cos(x) tg(x) ctg(x) nxn

l 1 2-Jx 1 x2 cos(x) — sin(x) 1 2 cos»(x) 1 sin2 (x) Y e ax cix aa 1 lnx X loga x 1 xln«правила дифференцирования [ c m ] Cf (x) (U ± V)

U ±V 1′ (m-v) f 1 uv + uv i,.4. л! :! X’t u v — u v, ‘!. «i : Г: «-*!. ;..п. v2 31

33 ПРИЛОЖЕНИЕ 4 Графическая иллюстрация корреляции $ 1 л3 Щ ы. е) 1 и * ^ т, *> п Н* Изображение на корреляционной плоскости пар одновременно измеренных результатов наблюдений двух величин х,- и ху : а) гц > 0 ; б) П/ 34 Литература 1. Захаров И. П. Теория неопределенности в измерениях. — Харьков: Консум, 2002, 256 с. 2. Guide to the Expression of Uncertainty in Measurement. -G e neva: ISO, p. 3. Бурдун Г. Д., Марков Б. Н. Основы метрологии. — М.: Изд-во стандартов, с. 4. ГОСТ Государственная система обеспечения единства измерений. Классы точности средств измерений. Общие требования. — М. : Государственный комитет СССР по стандартам, с. 5. Захаров И. П. Расчет коэффициента охвата для нормально и равномерно распределенных составляющих неопределенности // Системи обробки шформацй, 2005, вип. 6, стор ДСТУ РМГ 43:2006. Застосування «Руководства по оцениванию неопределенности измерений». 7. Захаров И. П., Климова Е. А. Расчет значений коэффициента Стьюдента для дробного числа степеней свободы // Системи обробки шформацп, 2010, вип. 4(85), с

35 U. _ I СОДЕРЖАНИЕ Предисловие 1 Что такое неопределенность измерений? 5 2 Основные принципы оценивания неопределенности измере- 6 ний 3 Источники неопределенности измерений Наблюдаемое рассеивание показаний Характеристики НСП 12 4 Базовый алгоритм оценивания неопределенности измерений Составление модельного уравнения Оценивание входных величин Вычисление оценки результата измерения Вычисление стандартных неопределенностей входных величин Вычисление вклада неопределенности входной величины в неопределенность измеряемой величины Определение стандартной неопределенности выходной величины (суммарной стандартной неопределенности) Вычисление коэффициента охвата Вычисление расширенной неопределенности Запись полного результата измерения Составление бюджета неопределенности 23 5 Учет корреляции при оценивании неопределенности входных величин Расчет суммарной стандартной неопределенности для коррелированных данных Проверка значимости коэффициента корреляции вычисленного по ограниченному количеству наблюдений 25 6 Взаимный пересчет характеристик погрешности и неопределенности измерений Пересчет от характеристик погрешности к оценкам неопределенности измерений Пересчет от неопределенности к характеристикам погрешности измерений 28 Приложения 33 Литература 33 34

36 Уважаемые коллеги! Кафедра метрологии и измерительной техники Харьковского национального университета радиоэлектроники на хоздоговорной основе предлагает осуществить: Разработку процедур оценивания неопределенности всех видов измерений при проведении испытаний и калибровок любых типов средств измерительной техники (СИТ) в соответствии с требованиями стандарта ДСТУ ISO/IEC 17025:2006 и «Положению НАЛУ про переходной период по обеспечению прослеживаемости измерений» от г. обучение персонала на базе Вашего предприятия по оцениванию неопределенности измерений при испытаниях и калибровках СИТ. Для получения подробной информации обращаться к автору этой книги (контактная информация имеется на сайте Желаю всем полной определенности в работе и личной жизни! П.П. Захаров 35

Видео:Инструкция онлайн-калькулятора для расчета составляющей неопределенности измеренийСкачать

Методика оценивания результата измерений и его неопределенности

Оценивание результата измерений и его неопределенности проводится в следующей последовательности:

-составление уравнения измерений;

-оценка входных величин и их стандартных отклонений (неопределенностей);

-оценка измеряемой (выходной) величины и ее неопределенности;

— составление бюджета неопределенности;

-оценка расширенной неопределенности результата измерений;

-представление результата измерений.

Рассмотрим эти составляющие подробнее.

I . Составление уравнения измерения

В качестве основы для составления уравнения измерения используется классическое уравнение связи: зависимость Y = f(X₁, X₂,…X_k). Далее в результате анализа условий измерений и используемых СИ, устанавливаются другие факторы, влияющие на результат измерений, и они также включаются в уравнение связи в качествевеличин X_k ₊₁ , X_k ₊₂ ,… X_m .

В итоге в рамках концепции неопределенности под уравнением измерения будет пониматься математическая зависимость между измеряемыми величинами X ₁ , X ₂ ,… X_k , а также другими величинами, влияющими на результат измерения X_k ₊₁ , X_k ₊₂ ,… X_m , и самим результатом измерения Y

(П2.1)

Величины X ₁ , X ₂ ,… X_m можно считать входными величинами, используемые для оценивания неопределенности результата измерения, а результат измерения Y – выходной величиной измерения.

II . Оценка входных величин и их стандартных отклонений (неопределенностей)

Пусть имеются результаты n_i измерений входной величины X_i, где i = 1…m. Как известно, при нормальном распределении наилучшей оценкой этой величины является среднее арифметическое

(П2.2)

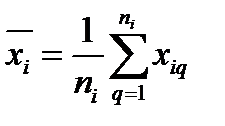
Стандартную неопределенность типа А определяют как среднеквадратическое отклонение по формуле:

(П2.3)

Для вычисления стандартной неопределенности по типу В используют:

-данные о предыдущих измерений величин, входящих в уравнение измерения;

— сведения, имеющиеся в метрологических документах по поверки, калибровки и сведения изготовителя о приборе;

— сведения о предполагаемом вероятностном распределении значений величин, имеющихся в научно-технических отчетах и литературных источниках;

— данные, основанные на опыте исследователя или общих знаниях о поведении и свойствах соответствующих (подобных) СИ и материалов;

— неопределенность используемых констант и справочных данных;

— нормы точности измерений, указанные в технической документации на методы и СИ;

— другие сведения об источниках неопределенностей, влияющих на результат измерения.

Неопределенности этих данных обычно представляют в виде границ отклонения значения величины от ее оценки. Наиболее распространенный способ формализации неполного знания о значении величины заключается в постулировании равномерного закона распределения возможных значений этой величины в указанных границах ±b_i для i-ой входной величины. При этом стандартную неопределенность по типу В определяют по следующей формуле

(П2.4)

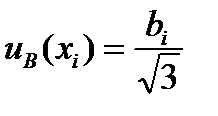
В случае других законов распределений формулы для вычисления неопределенности по типу В будут другие. В частности, если известно одно значение величины X_i, то это значение принимается в качестве оценки. При этом стандартную неопределенность вычисляют по формуле

(П2.5)

где U_p – расширенная неопределенность, k – коэффициент охвата. Если коэффициент охвата не указан, то, с учетом имеющихся сведений, принимают предположение о вероятностном распределении неопределенности величины X_i. Если такие сведения отсутствуют, то для определения коэффициента охвата можно воспользоваться данными таблицы П2.2 [П2.1].

Таблица П2.2

Предполагаемое распределение неопределенности входной величины	Вероятность охвата Р, которой соответствует U ( x _i )	Коэффициент охвата k
0,99 – 1,0	1,71 — 1,73
0,95	1,65
1,0 (предел допускаемых значений)	3
0,997	3
0,99	2,6
0,95	2
Неизвестное распределение	2

Коэффициенты охвата для равномерного распределения, представленные в табл.П2.2, определены следующим образом. Для симметричных границ окончательного равномерного распределения СКО вычисляется по формуле (П2.4). Тогда расширенную неопределенность можно записать в виде . При расширенной неопределенности, соответствующей вероятности P=0,95 и границе равномерного распределения b=1, коэффициент k=0,95 . = 1,65.

При расширенной неопределенности, соответствующей вероятности P=0,99, коэффициент k= 0,9995· = 1,71. При расчетах принималось, что =1,73 и площадь под равномерным распределением соответствует единице и, соответственно, при Р= 1коэффициентk=1,73.

Если известны граница суммы неисключенных систематических погрешностей, распределенных по равномерному (равновероятному) закону θ(Р) или расширенная неопределенность в терминах концепции неопределенности U_p, то коэффициент охвата при числе неисключенных систематических погрешностей m>4, зависит от доверительной вероятности. Коэффициент охвата kравен1,1 при Р=0,95; и1,4 при Р=0,99 [П2.1].

Неопределенности входных величин могут быть коррелированны. Для вычисления коэффициента корреляции r(x_i, x_q) используют согласованные пары результатов измерений , где w = 1, 2,…,n_ij; n_ij – число согласованных пар результатов измерений Вычисления проводят по известной формуле из статистики и теории вероятности

(П2.6)

Значимость коэффициента корреляции определяется критерием отсутствия или наличия связи между аргументами.

III . Оценка измеряемой (выходной) величины и ее неопределенности

Оценку измеряемой величины y вычисляют как функцию оценок входных величин X ₁ , X ₂ ,… X_m, по формуле (П2.1), предварительно внеся на все источники неопределенности, имеющие систематический характер, – поправки.

Вычисление суммарной неопределенности выходной величины проводят по тем же формулам, которые используются для расчета погрешностей косвенных измерений в классической концепции погрешности измерений.

В случае некоррелированных оценок входных величин, суммарную стандартную неопределенность вычисляют по формуле

(П2.7)

и в случае коррелированных оценок – по формуле

(П2.8)

где — коэффициент корреляции; — стандартная неопределенность i-ой – входной величины, вычисленная по типу А или типу В; — коэффициенты чувствительности выходной величины по отношению ко входной величине x_i .

IV . Составление бюджета неопределенности

Под бюджетом неопределенности понимается формализованное представление полного перечня источников неопределенности измерений по каждой входной величине с указанием их стандартной неопределенности и вклада их в суммарную стандартную неопределенность результата измерений.

V . Оценка расширенной неопределенности результата измерений

Расширенная неопределенность равна произведению стандартной неопределенности u(y) результата измерений на коэффициент охвата k:

Руководство по неопределенности [П2.1] рекомендует рассматривать все результаты измерений при доверительной вероятности (вероятности охвата) Р=0,95. При этой вероятности преимущественно определяют число степеней свободы по эмпирической формуле Велча-Саттерствейта

(П2.10)

При этом коэффициент охвата определяется при вероятности Р=0,95 с использованием таблицы распределения Стьюдента по формуле

, (П2.11)

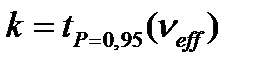
Коэффициент охвата ( округлены до ближайшего целого числа)

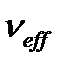	3	4	5	6	7	8	9	10	16	20	30
t_P=0,95	3,182	2,776	2,571	2,447	2,365	2,306	2,262	2,228	2,120	2,086	2,042	1,960
t_P=0,99	5,841	4,604	4,032	3,707	3,499	3,355	3,250	3,169	2,921	2,845	2,750	2,576

Формулу для оценки суммарной стандартной неопределенности (П2.7) можно записать в более простом виде

, (П2.12)

также как и формулу (П2.10) для определения числа степеней свободы

, (П2.13)

где — число степеней свободы при прямых измерениях входной величины, n – число измерений, — оценка стандартных неопределенностей, вычисленных по типу А и по типу В, соответственно.

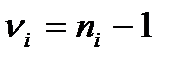
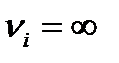
При оценке вклада неопределенности (см.формулу П2.10) по типу А принимают , по типу В . При этих условиях, легко показать из формулы (П2.10), что, если по типу А оценивается неопределенность только одной входной величины, то формула (П2.10) упрощается

, (П2.14)

где n_A – число повторных измерений входной величины, оцениваемой по типу А.

VI . Представление результата измерений

При представлении результатов измерений Руководство рекомендует приводить достаточное количество информации, чтобы можно было проанализировать и/или повторить весь процесс получения результата измерений и вычисления неопределенностей, а именно:

— алгоритм получения результата измерений;

— алгоритм расчета всех поправок для исключения систематических погрешностей и их неопределенней;

— неопределенности всех используемых данных и способы их получения;

— алгоритмы вычисления суммарной и расширенной неопределенностей, включая значение коэффициента охватаk .

Таким образом, в документации по результатам измерений необходимо представлять:

u_c – суммарную неопределенность;

U_p – расширенную неопределенность;

k – коэффициент охвата;

u_i – данные о входных величинах;

— эффективное число степеней свободы.

Например, если результатом измерения является электросопротивление, то при оформлениирезультата измерений, записывают: «Электросопротивление резистора составляет 163,2 Ом. Расширенная неопределенность результата измерений составляет ± 2,4 Ом при коэффициенте охвата равном 2» или «измерения показали, что электросопротивление резистора находится в интервале (160,8 – 165,6) Ом при коэффициенте, равном 2». По умолчанию предполагается, что эти результаты соответствуют вероятности охвата 0,95.

Несмотря на то, что нормативный документ РМГ 43-2001[П2.2] на территории России не действует (вместо него введен в действие ГОСТ Р 54500-2011 [П2.3]), приведенные в нем примеры очень понятны и могут дать необходимое представление о том, как проводить оценку неопределенности результатов измерений.

Пример из РМГ 43-2001

1) Приведем данные, имеющиеся в распоряжении оператора, задача которого состоит в измерении силы тока с помощью вольтметра и токового шунта.

1 Составление уравнения измерения

(1-П2)

где I – сила измеряемого тока, V – напряжение на шунте, которое непосредственно измеряется для определения силы тока, R– сопротивление шунта, t°C – температура окружающей среды, способная повлиять на результат измерения силы тока.

1.2. Производится многократное (n=10) измерение напряжения с помощью вольтметра на сопротивлении шунта при температуре t = (23,00±0,05)°С.

Границы неисключенной систематической погрешности вольтметра в милливольтах определены при его калибровке в виде следующего выражения:

1.3. Сопротивление шунта определено при его калибровке для тока величиной I=10 А и температуре t=23,00°C и равно R₀ = 0,010 088 Ом. Относительные границы неисключеннойсистематической погрешности сопротивления шунта, установленные при его калибровке, равны

1.4. Границы неисключенной систематической составляющей погрешности значения сопротивления шунта, обусловленной погрешностью измерений температуры, находят из формулы, определяющей зависимость сопротивления от температуры

где R₀ – значение сопротивления при t = t₀ (t₀=23,00°C; R₀ = 0,010 088 Ом); α – температурный коэффициент (a = 6∙10 -6 К -1 ). В случае, когда границы погрешности измерения температуры составляют Dt, границы соответствующей составляющей погрешности значения сопротивления равны

2 Нахождение результата измерений

В результате серии из n=10 измерений получают ряд значений V_i в милливольтах:

100,68; 100,83; 100,79; 100,64; 100,63; 100,94; 100,60; 100,68; 100,76; 100,65.

Среднеарифметическое вычисляют по формуле (П2.2)

мВ (6-П2)

Результат измерения силы тока получают по формуле

Ом

3 Анализ источников погрешности результата измерений

3.1. Среднеквадратическое отклонение (СКО), характеризующее случайную составляющую погрешности при измерениях напряжения , вычисляют по формуле (П2.3)

или (7-П2)

Примечания. 1) Значок d здесь и далее обозначает относительное значение величины.

2) В соответствии с рекомендациями Руководства симметричные интервалы не обозначаются значками ±.

3.2. Границы неисключенной систематической погрешности вольтметра в милливольтах при в соответствии с формулой (2-П2), будут равны

= 5,0× 10 -2 мВ или 0,050% (8-П2)

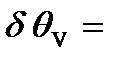
3.3. Границы неисключенной систематической погрешности сопротивления шунта, в соответствии с (3-П2) и (4-П2), установленные при его калибровке, равны

Ом или (9-П2)

3.4. Границы неисключенной систематической составляющей погрешности значения сопротивления шунта, обусловленной погрешностью измерений температуры в соответствии с (5-П2) равны

В дальнейшем эту составляющую погрешности ввиду ее малости по сравнению с другими составляющими можно не учитывать.

4 Вычисление характеристик погрешности результата измерений

Для вычисления результирующей погрешности измерения, состоящей из случайной погрешности и суммы неисключенных погрешностей, используется формула, принятая в Государственной системе обеспечения единства измерений для косвенных измерений:

(11-П2)

где все составляющие погрешности определены при одной и той же доверительной вероятности Р. В числителе сумма доверительных границ случайной и суммарной неисключеннойпогрешности, в знаменателе — сумма СКО случайной и СКО суммарной неисключенной систематической погрешности, а — СКО суммарной погрешности измерения.

Примечание. Эта формула действительна при соотношении Если систематическая составляющая погрешности мала, т.е. 8,0, то — Заметим, что для общности составляющие погрешности представляются в виде

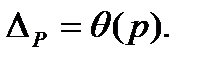
Ниже приводится вычисление всех составляющих погрешностей, входящих в формулу (11-П2).

4.1. Делается предположение о равномерном распределении неисключенных систематических составляющих погрешности результата измерений внутри их границ q_Vи q_R_. Тогда СКО суммарной неисключенной систематической составляющей погрешности результата измерений силы тока S_q определяют по формуле

(12-П2)

В этой формуле учтено, что коэффициенты влияния

4.2. Доверительные границы суммарной неисключенной систематической погрешности результата измерений силы тока q(р) при доверительной вероятности Р=0,95 оценивают по формуле

(13-П2)

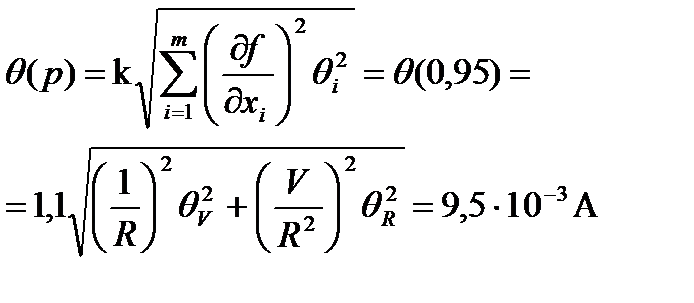
4.3. СКО случайной составляющей погрешности результата измерений силы тока S определяется по формуле

(14-П2)

4.4. СКО суммарной погрешности результата измерений силы тока будет равно

— (15-П2)

4.5. Доверительные границы погрешности результата измерений силы тока при вероятности 0,95 и эффективном числе степеней свободы , вычисленные по формуле (11-П2), дают результат

5 Вычисление неопределенности измерений

5.1. По типу А вычисляют стандартную неопределенность, обусловленную источниками неопределенности, имеющими случайный характер. Формула для вычислений подобна (7-П2)

мВ (17-П2)

Стандартную неопределенность силы тока, обусловленную источниками неопределенности, имеющими случайный характер, определяют по формуле

(18-П2)

5.2. По типу В вычисляют стандартные неопределенности, обусловленные источниками неопределенности, имеющими систематический характер. Закон распределения величин внутри границ считают равномерным.

Границы систематического смещения при измерениях напряжения, определенные при калибровке вольтметра, определяются соотношением (2-П2). Тогда соответствующую стандартную неопределенность u_B _, _V вычисляют по формуле

(19-П2)

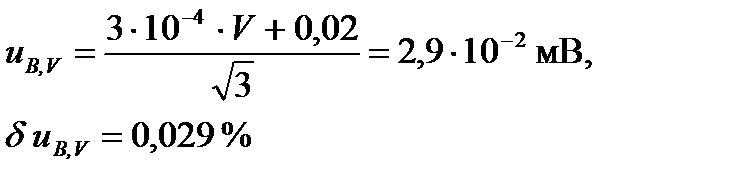
Границы, внутри которых лежит значение сопротивления шунта, определены при калибровке шунта и равны 7×10 -4 ×R. Тогда при R=R₀ соответствующую стандартную неопределенность вычисляют по формуле

(20-П2)

Границы изменения значения сопротивления шунта, обусловленного изменением температуры, равны Соответствующую стандартную неопределенность получают в соответствии с формулой

(21-П2)

В дальнейшем этой составляющей неопределенности ввиду ее малости по сравнению с другими составляющими можно пренебречь.

Суммарную стандартную неопределенность u_B, вычисленную по типу В, определяют по формуле

(22-П2)

5.3. Суммарную стандартную неопределенность u_C вычисляют по формуле

(23-П2)

5.4. Эффективное число степеней свободы рассчитывают по формуле (10)

(24-П2)

5.5. Коэффициент охвата k находят по таблице 4 и определяют по формуле

(25-П2)

5.6. Расширенную неопределенность U_0,95 определяют следующим образом

(26-П2)

6 Сравнение результата вычислений различными методами

Сравнение результата вычислений погрешности измерений в доверительном интервале, соответствующем вероятности Р=0,95 и расширенной неопределенности с коэффициентом охвата равном двум, т.е. соответствующем уровню доверия 0,95. совпадают и равны 0,012 А.

Следует отметить, что это не случайно, поскольку в основе расчетов лежат одни и те же измерительные данные и одни те же подходы к распределениям различных переменных. Сравнения результатов измерений, определенных с помощью классического подхода и концепции неопределенности, как показано на многочисленных примерах в различных публикациях дают одни и те же окончательные результаты [П2.1, П2.2].

Однако результат, полученный в концепции неопределенности, трактуется иначе, чем результат, полученный при применении классического подхода. В концепции неопределенности не используются понятия истинного и действительного значений измеряемой величины. Результат измерения — вот что считается реальностью, поскольку величину истинного значения никто не знает. Расширенная неопределенность трактуется в Руководстве как интервал, содержащий заданную долю распределения значений, которые могли быть обосновано приписаны измеряемой величине.

Вообще расширенная неопределенность в концепции неопределенности не играет той роли, которая отводится в концепции погрешности. Считается, что основным результатом оценки является суммарная неопределенность u_C, а расширенная неопределенность отличается от нее на постоянный коэффициент, который необходим в ряде специальных случаев для показа надежности оценки. Этот коэффициент может принимать значения от 2 до 3, при уровне доверия от 0,95 до 0,99.

Наши незнания об измеряемой величине определяются неопределенностью и группируются около результата измерения.

Список литературы, используемой в Приложении 2.

П2.1. А.Э. Фридман Основы метрологии. Современный курс. – С.-Пб.: НПО «Профессионал», 2008.

П2.2 РМГ 43-2001 Применение «Руководства по выражению неопределенности измерений», рекомендации по межгосударственной стандартизации, Межгосударственный совет по стандартизации, метрологии и сертификации, Минск, Изд-во стандартов, 2002

П2.3 ГОСТР 54500.1-2011/ Руководство ИСО/МЭК 98-1: 2009 Неопределенность измерения. Часть 1. Введение в руководства по неопределенностям измерения. – М.: Стандартинформ, 2012. – 17 с.