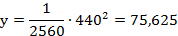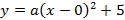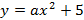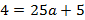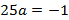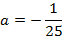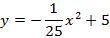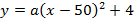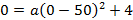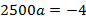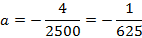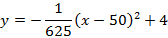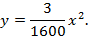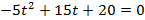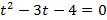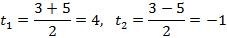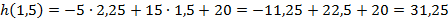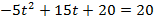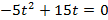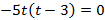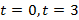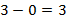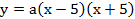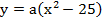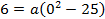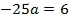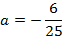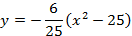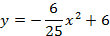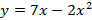- Ваш ответ
- Похожие вопросы
- Урок_3_Решение текстовых задач_Методические рекомендации
- Арка моста имеет форму параболы составьте уравнение
- Исследовательские работы и проекты
- Параболы в арочных мостах
- Подробнее о работе:
- Оглавление
- Введение
- Парабола
- Парабола в колокольчике
- Из истории мостостроения в России с XII по XIX века
- 🔍 Видео
Видео:Парабола. Под сводом арки. STEAM урокСкачать

Ваш ответ
Видео:Всё о квадратичной функции. Парабола | Математика TutorOnlineСкачать

Похожие вопросы
- Все категории
- экономические 43,289
- гуманитарные 33,621
- юридические 17,900
- школьный раздел 607,151
- разное 16,830
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Видео:Как легко составить уравнение параболы из графикаСкачать

Урок_3_Решение текстовых задач_Методические рекомендации
Методические рекомендации к уроку №3
темы/подраздела « Квадратичная функция и ее график »
раздела « Квадратичная функция»
Тема урока: Решение текстовых задач
8. 4 .2.3 использовать квадратичную функцию для решения прикладных задач;
8.4.3.1 составлять математическую модель по условию задачи.
На данном уроке учащиеся продолжат работу по развитию навыка решения задач с использованием квадратичной функции.
Методические рекомендации по организации урока. Рекомендации по формативному оцениванию
В начале урока учащимся предлагается тестовые задания для организации повторения пройденного материала. Учитель заранее готовит сигнальные карточки трех цветов для каждого ученика. Их использование позволит учителю быстро оценить понимание учащимися определенного материала. Допущенные ошибки сразу анализируются.
Затем проводится письменная работа, она с совместного разбора задания на составление уравнения функции и поиска ответа на вопрос задачи. Учитель вовлекает всех учащихся в диалог. Для первоначального закрепления учащиеся решают задачу в группах. Здесь нужно нацелить их на то, что каждый ученик после обсуждения должен уметь объяснить решение задачи свой группы. Процесс объяснения другим учащимся позволит глубже разобраться в решении. Также здесь нужно поощрять учащихся, задающих вопросы. Учитель обходит класс, слушает объяснения, помогает в корректном применении математического языка.
Два задания подготовлены для самостоятельного решения учащимися. Учитель обходит класс, дает советы учащимся. Он может также привлекать других учащихся для консультирования тех, кто испытывает затруднения.
Ответы и решения
Мост Голден Гейт через пролив Золотые ворота находится в Сан-Франциско (США). Мост построен по проекту инженера Йозефа Штрауса. Строительство началось в 1933 году и было закончено через 4 года. Мост установил два рекорда: как самый длинный и как самый высокий мост.
Длина основного пролета моста (расстояние между опорами) 1280 м, высота опор над уровнем проезжей части моста – 160 м. Кабель, поддерживающий мост, имеет форму параболы и касается проезжей части в середине пролета. На какой высоте находится кабель на расстоянии 200 м от опоры моста?
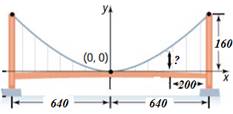
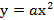
Точка (640, 160) – расположена на одной из опор, отсюда 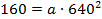
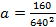
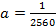
Тогда уравнение параболы имеет вид: 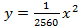
Кабель находится на расстоянии 200 м от опоры моста, следовательно, в 440 м от вершины параболы.
Задание для группы 1
Дорога проходит под параболической аркой, как показано на рисунке. Самая высокая часть арки – 5 м. Ширина дороги – 10м, а высота – 4 м. Составьте квадратичную функцию, задающую форму арки.
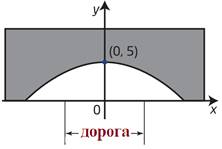
Запишем уравнение параболы в виде 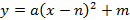
Ширина дороги – 10м, а высота – 4 м, значит парабола проходит через точку 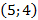
Ответ : 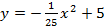
Задание для группы 2
Небольшие мосты имеют форму параболы. На рисунке представлен один из таких мостов. Составьте уравнение параболы, определяющей форму этого моста.
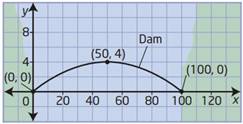
Запишем уравнение параболы в виде 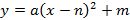
Парабола проходит через точки 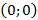
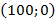
Ответ : 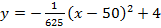
Задание для группы 3
Длина моста 400 м, а высота опор 75 м. Напишите уравнение параболы, являющейся моделью для подвесного кабеля, удерживающего этот мост.

Построим координатную плоскость, так чтобы ось х проходила вдоль проезжей части моста, а ось у – вдоль оси симметрии. Тогда вершина параболы имеет координаты (0, 0), значит функция задается формулой 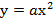
Парабола проходит через точку (200; 75), тогда 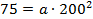
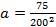
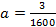
Тогда уравнение параболы имеет вид:
1. Тело брошено вертикально вверх. Высота ( h ), на которой находится тело через t секунд полета, вычисляется по формуле 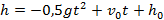
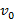
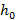
Составьте формулу, задающую эту зависимость, если h0 = 20, v0 = 15 и постройте график.
Используя график, ответьте на вопросы:
а) Сколько времени тело двигалось вверх?
б) Сколько времени тело двигалось вниз?
в) На какую максимальную высоту поднялось тело?
г) В течении какого времени тело находилось на высоте более 20 м?
Функция имеет вид 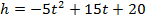
а) 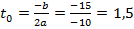
б )
Через 4 с тело упало на землю.
Тело двигалось вниз 2,5 с.
в)
г )
Ответ: Тело находилось на высоте более 20 м в течение 3 с.
2. Двух полосная дорога со встречным движением проходит под аркой шириной 10 м. Самая высокая точка арки расположена на высоте 6 м. Сможет ли грузовик, высота которого 4,5 м, а ширина 3 м, проехать под этой аркой? Ответ объясните.
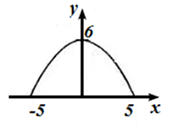
Если расположить координатную плоскость, так чтобы ось х проходила вдоль проезжей части дороги, а ось у – вдоль оси симметрии, тогда вершина параболы имеет координаты (0, 6) . Парабола проходит через точки 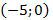
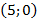
Подставив координаты точки 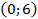
Ширина грузовика 3 м, тогда при 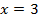
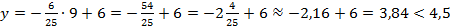
Ответ: Грузовик может проехать под этой аркой .
Найдите наибольшее или наименьшее значение функции.
a) 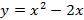
b) 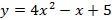
c)
Определите коэффициенты функции 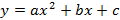
а) 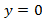
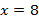
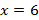
б) 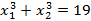
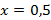
в) наименьшее значение функции, равное 7, достигается при 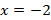
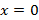
Список полезных ссылок и литературы
1. Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Феоктистов И.Е. Алгебра. 9 класс : учеб. для учащихся общеобразоват. учреждений. – М.: Мнемозина, 2010
2. Виленкин Н.Я., Сурвилло Г.С. Алгебра. 9 класс. учеб. Для учащихся с углубленным изучением математики. / 7-е изд. — М.: Просвещение, 2006.
Видео:Вариант 72, № 5. Уравнение оси симметрии параболы. Пример 2Скачать

Арка моста имеет форму параболы составьте уравнение
Видео:Вершина параболы и ось симметрии. ПримерСкачать

Исследовательские работы и проекты
Видео:Построение параболы по ее директрисе и фокусуСкачать

Параболы в арочных мостах
В процессе работы над индивидуальным исследовательским проектом по математике на тему «Параболы в арочных мостах» автором была поставлена цель, изучить материал о свойствах квадратичной функции и ее графика — параболы, исследовать графики квадратичной функции в арочных мостах Санкт-Петербурга.
Подробнее о работе:
Учебная исследовательская работа по математике на тему «Параболы в арочных мостах» будет интересна учащимся 9 класса, рассматривает теоретическую базу о построении арочных мостов с применением принципа параболы. В работе исследуется парабола в мостостроении, проводится анализ построения Санкт-Петербургских арочных мостов: Казанского, Синего, Троицкого, моста в Юсуповском саду и Арки-галереи над Зимней канавкой.
В исследовательском проекте по математике представлена теория квадратичной функции и ее графика, найдены арочные мосты в Петербурге и представлены их фотографии. На фотографиях арочных мостов города Санкт-Петербурга автор схематично изобразил параболу, расположенную на оси координат, и произвел вычисление уравнений графиков квадратичной функции, изучил их свойства.
Оглавление
Введение
1. Что такое парабола?
1.1. Парабола – график квадратичной функции.
1.2. Из истории мостостроения в России с XII по XIX века.
1.3. Виды мостов.
1.4. Арочные мосты.
2. Парабола в мостостроении.
2.1. Казанский мост.
2.2. Арка-галерея над Зимней канавкой.
2.3. Мост в Юсуповском саду.
2.4. Синий мост.
2.5. Троицкий мост.
Заключение
Используемая литература
Приложения
Введение
- Изучить материал о свойствах квадратичной функции и ее графика- параболы.
- Исследовать графики квадратичной функции в арочных мостах Санкт-Петербурга.
Для достижения цели я поставила следующие задачи:
- Изучить литературу про мосты Санкт-Петербурга.
- Изучить теорию квадратичной функции и ее графика.
- Найти арочные мосты в Петербурге.
- Сфотографировать эти мосты.
- Овладеть методикой задания уравнениями графиков квадратичной функции и исследовать их свойства.
Объект исследования: арочные мосты Санкт-Петербурга
Предмет исследования: свойства параболы, применяемые при строительстве арочных мостов Санкт-Петербурга
Продукт научно-исследовательской работы: презентация, включающая фотографии мостов Санкт-Петербурга, сделанные автором.
Видео:Как определить уравнение параболы по графику?Скачать

Парабола
Существует довольно много видов функций: линейная, квадратичная, степенная, показательная, логарифмическая, тригонометрическая и другие, каждая из них задается уравнением и графиком. Линейная функция задается прямой, квадратичная – квадратичной параболой, степенная функции вида у=х2k+1 (где k – натуральное число) — кубической парабола, функция вида y – гиперболой и тд. В данной работе будут рассмотрены исключительно квадратичная функция и ее график.
Функция вида y=ax2+bx+c, где a, называется квадратичной. Графиком этой функции является парабола. Парабола – это геометрическое место точек, равноудаленных от данной прямой и данной точки.
Чтобы построить график функции вида y=ax2+bx+c, нужно найти координаты вершины графика.
Х вершины = (-b)/2a; для нахождения у вершины нужно подставить значение найденного x в данное уравнение;
график функции y=ax2+bx+c получается из графика функции у=aх2 сдвигом в точку (х вершины; у вершины).
Довольно часто мы сталкиваемся с параболическими формами. Например, во время или после дождя мы наблюдаем радугу. В лепестках некоторых цветов, в очертании горных хребтов и вершин можно разглядеть параболу.
Видео:Построение параболыСкачать

Парабола в колокольчике
Гуляя по городу, мы часто видим дугообразные конструкции. Архитекторы используют параболическую форму в проектировании арок, мостов, куполов, потолков. Во-первых, именно такая форма придает эстетичный вид, во-вторых, параболическим конструкциям присуща прочность, потому что сила, создаваемая нагрузкой на мост или арку, не толкает вниз, а распределяется вдоль дуги, то есть эти строения поддерживают сами себя. В куполах всех храмов и церквей используется этот же принцип. В данной работе будут рассмотрены мосты в Санкт-Петербурге.
Прежде чем рассматривать виды мостов и их преимущества, познакомимся с историей мостостроения в России.
Видео:Задача про арку Как рассчитать высоту опор арочного мостаСкачать

Из истории мостостроения в России с XII по XIX века
Постройка мостов, вероятно, началась очень давно. При Владимире Мономахе в 1115 году был построен наплавной мост через Днепр в Киев, при Дмитрии Донском во время осады Твери были построены 2 моста, а во время войны с татарами в 1380 году возвели мост через Дон. Кроме того, в Новгородской летописи упоминается о «разборчатых» мостах в Новгороде через реку Волхов(рис.4).
Наплавные мосты состояли из закрепленных между собой плотов и лодок. Именно наплавные мосты были наиболее распространены в России в этот период из-за простоты и дешевизны конструкции.
Возводной мост, прилегавший к городской стене, делался подъемным. Первое указание относительно употребления таких мостов относится к 1229 году. Механизм, приводивший мост в движение, состоял из коромысла, который вращался между столбами, и цепей.
Первый каменный мост начали строить в 1643 году при Михаиле Федоровиче Романове, однако в связи со смертью царя в 1645 году строительство было остановлено. Только в 1687 году первый каменный мост был открыт.
С воцарением Петра Великого инженерное искусство развивалось неимоверно быстро, но при царе мостов не строилось. Петр I воспринимал Петербург как крупнейший порт, куда прибывали суды всех стран Европы, а мосты мешали судоходству. Также в городе на Неве ежегодно случались наводнения и штормовые бури, которые могли повредить конструкции. Но все же Петр I сделал исключение, издав приказ о строении деревянного моста, соединявшего Березовый и Заячий острова, с целью транспортировки грузов к Петропавловской крепости.
В царствование Екатерины I в 1727 году был возведен первый наплавной мост через Неву. При Анне Иоанновне возвели несколько каменных мостов на сваях, например, Симеоновский через Фонтанку, оформленный под каменный арочный мост. Остальные мосты через Мойку и Фонтанку построены в период времени 1742-1749гг., т.е. во время правления Елизаветы Петровны. При ней же был возведен Исаакиевский мост(рис.4).
При Екатерине II в Петербурге началась замена деревянных мостов на каменные на реке Фонтанке, строение Казанского и Каменного мостов через Екатерининский канал[2], в Москве через реку Яузу был возведен Дворцовый мост. С началом строительства в 1817 году Петербурго-Московского шоссе появилось множество каменных мостов, пролеты которых могли достигать 9 саж[3]. В 40-х годах строилось несколько каменных мостов в Тифлисе[4], например, Михайловский мост с пролетом в 15 саж (32м).
Чугунные арочные мосты впервые появились в 1806 году в Петербурге при Александре I, это были первые металлические мосты в России. Были построены Полицейский, Красный, Синий, Поцелуев, Мало-Семеновский мосты.
Цепные мосты введены в Россию в 1822 году по предложению французских инженеров. Распространение таких мостов захватило период с 1824 по 1853 год. К цепным мостам относятся Пантелеймоновский, пешеходные через Екатерининский канал и Мойку, Египетский, проволочный Лиговский через Западный Бур в Брест, мост через Нарву в Ивангород, Киевский через Днепр и Островский через реку Великую.
До 1873 года из подвижных мостов с постоянными опорами применялись только подъемные с горизонтальной осью вращения. Поворотные мосты появились в первые в 1850 году при строительстве Николаевского моста в Петербурге и цепного моста в Киеве в 1853 году.
🔍 Видео
Фокус и директриса параболы 1Скачать

Как строить параболу? | TutorOnlineСкачать

§24 Каноническое уравнение параболыСкачать

213. Фокус и директриса параболы.Скачать

Уравнение окружности (1)Скачать

Видеоурок "Парабола"Скачать

Квадратичная функция. Вершина параболы и нули функции. 8 класс.Скачать

Определение знаков коэффициентов квадратного уравнения (параболы) по рисунку/ЗНО 2010 #25Скачать

Составить уравнение окружности. Геометрия. Задачи по рисункам.Скачать

Висячие мосты, арифметическая прогрессия и параболаСкачать

2. Все про параболу | Задание 9 | ЕГЭ Математика | Аня Матеманя | ТопскулСкачать