13 задание егэ математика профиль как решать тригонометрические уравнения

13 задания профильного ЕГЭ по математике представляет собой уравнение с отбором корней принадлежащих заданному промежутку. Одним из видов уравнений которое может оказаться в 13 задание является тригонометрическое уравнение. Как правило, это достаточно простое тригонометрическое уравнение для решения которого потребуется знания основных тригонометрических формул, и умение решать простейшие тригонометрические уравнения. Отбор корней тригонометрического уравнения принадлежащих заданному промежутку можно производить одним из четырех способов: методом перебора, с помощью тригонометрической окружности, с помощью двойного неравенства и графическим способом. В данном разделе представлены тригонометрические уравнения (всего 226) разбитые на три уровня сложности. Уровень А — это простейшие тригонометрические уравнения, которые являются подготовительными для решения реальных тригонометрических уравнений предлагаемых на экзамене. Уровень В — состоит из уравнений, которые предлагали на реальных ЕГЭ и диагностических работах прошлых лет. Уровень С — задачи повышенной сложности.

Видео:КОГДА ПИСАТЬ +Пк, а когда +2Пк? (Задание 13 по Тригонометрии ЕГЭ 2024 по Математике Профиль)Скачать

Задание №13 ЕГЭ по математике профильного уровня

Видео:Тригонометрические уравнения. ЕГЭ № 12 | Математика | TutorOnline tutor onlineСкачать

Уравнения

В 13 задании профильного уровня ЕГЭ по математике необходимо решить уравнение, но уже повышенного уровня сложности, так как с 13 задания начинаются задания бывшего уровня С, и данное задание можно назвать С1. Перейдем к рассмотрению примеров типовых заданий.

Разбор типовых вариантов заданий №13 ЕГЭ по математике профильного уровня

Первый вариант задания (демонстрационный вариант2018)

Алгоритм решения:

1. При помощи тригонометрических формул приводим уравнение к виду, содержащему только одну тригонометрическую функцию.
2. Заменяем эту функцию переменной t и решаем получившееся квадратное уравнение.
3. Делаем обратную замену и решаем

Простейшие (Protozoa) — тип одноклеточных животных.

1. Строим числовую ось.
2. Наносим на нее корни.
3. Отмечаем концы отрезка.
4. Выбираем те значения, которые лежат внутри промежутка.
5. Записываем ответ.

Решение:

сos2x = 1 – sin x.

Преобразуем левую часть уравнения, используя формулу косинуса двойного аргумента, с использованием синуса:

Получаем такое уравнение: 1−sin 2 x=1− sinx Теперь в уравнении присутствует только одна тригонометрическая функция sinx. 2. Вводим замену: t = sinx. Решаем получившееся квадратное уравнение:

3. Делаем обратную замену:

Решаем эти уравнения:

Следовательно, получаем два семейства решений. Пункт б):

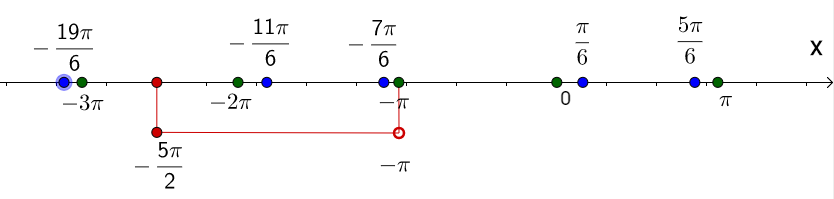
1. В предыдущем пункте получено два семейства, в каждом из которых бесконечно много решений. Необходимо выяснить, какие из них, находятся в заданном промежутке. Для этого строим числовую прямую.

2. Наносим на нее корни обоих семейств, пометив их зеленым цветом (первого) и синим (второго).

3. Красным цветом помечаем концы промежутка. 4. В указанном промежутке расположены три

Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.

Второй вариант задания (из Ященко, №1)

Алгоритм решения:

1. Заменяем эту функцию переменной t и решаем получившееся квадратное уравнение.
2. Делаем обратную замену и решаем простейшие показательные, потом тригонометрические уравнения.

1. Строим координатную плоскость и окружность единичного радиуса на ней.
2. Отмечаем точки, являющиеся концами отрезка.
3. Выбираем те значения, которые лежат внутри отрезка.
4. Записываем ответ.

Решение:

Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.

D=b 2 – c = 81 – 4∙4∙2 =49,

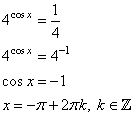
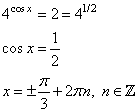
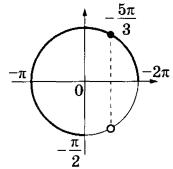
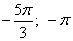
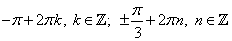
3. Возвращаемся к переменной х: Пункт б) 1. Строим координатную плоскость и окружность единичного радиуса на ней. 2. Отмечаем точки, являющиеся концами отрезка. 3. Выбираем те значения, которые лежат внутри отрезка.. Это корни . Их два. Ответ: а) б)

Третий вариант задания (из Ященко, № 6)

Алгоритм решения:

1. При помощи тригонометрических формул приводим уравнение к виду, содержащему только одну тригонометрическую функцию.
2. Заменяем эту функцию переменной t и решаем получившееся квадратное уравнение.
3. Делаем обратную замену и решаем простейшие показательные, а затем тригонометрические уравнения.

1. Решаем неравенства для каждого случая.
2. Записываем ответ.

Видео:Профильный ЕГЭ 2024. Задача 12. Тригонометрические уравнения. 10 классСкачать

Задания по теме «Тригонометрические уравнения»

Открытый банк заданий по теме тригонометрические уравнения. Задания C1 из ЕГЭ по математике (профильный уровень)

Видео:Щелчок по математике I №5,6,12 Тригонометрия с нуля и до ЕГЭ за 4 часаСкачать

Задание №1179

Условие

а) Решите уравнение 2(sin x-cos x)=tgx-1.

б) Укажите корни этого уравнения, принадлежащие промежутку left[ frac2;,3pi right].

Решение

а) Раскрыв скобки и перенеся все слагаемые в левую часть, получим уравнение 1+2 sin x-2 cos x-tg x=0. Учитывая, что cos x neq 0, слагаемое 2 sin x можно заменить на 2 tg x cos x, получим уравнение 1+2 tg x cos x-2 cos x-tg x=0, которое способом группировки можно привести к виду (1-tg x)(1-2 cos x)=0.

1) 1-tg x=0, tg x=1, x=fracpi 4+pi n, n in mathbb Z;

2) 1-2 cos x=0, cos x=frac12, x=pm fracpi 3+2pi n, n in mathbb Z.

б) С помощью числовой окружности отберём корни, принадлежащие промежутку left[ frac2;, 3pi right].

x_1=fracpi 4+2pi =frac4,

x_2=fracpi 3+2pi =frac3,

x_3=-fracpi 3+2pi =frac3.

Ответ

а) fracpi 4+pi n, pmfracpi 3+2pi n, n in mathbb Z;

б) frac3, frac3, frac4.

Видео:СЛИВ №13 из ЕГЭ 2024 по математике | Посмотри это, чтобы потом не плакатьСкачать

Задание №1178

Условие

а) Решите уравнение (2sin ^24x-3cos 4x)cdot sqrt =0.

б) Укажите корни этого уравнения, принадлежащие промежутку left( 0;,frac2right] ;

Решение

а) ОДЗ: begin tgxgeqslant 0\xneq fracpi 2+pi k,k in mathbb Z. end

Исходное уравнение на ОДЗ равносильно совокупности уравнений

left[!!begin 2 sin ^2 4x-3 cos 4x=0,\tg x=0. endright.

Решим первое уравнение. Для этого сделаем замену cos 4x=t, t in [-1; 1]. Тогда sin^24x=1-t^2. Получим:

t_1=frac12, t_2=-2, t_2notin [-1; 1].

4x=pm fracpi 3+2pi n,

x=pm fracpi +frac2, n in mathbb Z.

Решим второе уравнение.

tg x=0,, x=pi k, k in mathbb Z.

При помощи единичной окружности найдём решения, которые удовлетворяют ОДЗ.

Знаком «+» отмечены 1 -я и 3 -я четверти, в которых tg x>0.

Получим: x=pi k, k in mathbb Z; x=fracpi +pi n, n in mathbb Z; x=frac+pi m, m in mathbb Z.

б) Найдём корни, принадлежащие промежутку left( 0;,frac2right].

Ответ

а) pi k, k in mathbb Z; fracpi +pi n, n in mathbb Z; frac+pi m, m in mathbb Z.

Видео:Задание №13 (бывшее №12) с 0 и до уровня ЕГЭ за 7 часов | Математика ЕГЭ - УравненияСкачать

Задание №1177

Условие

а) Решите уравнение: cos ^2x+cos ^2fracpi 6=cos ^22x+sin ^2fracpi 3;

б) Укажите все корни, принадлежащие промежутку left( frac2;,frac2right].

Решение

а) Так как sin fracpi 3=cos fracpi 6, то sin ^2fracpi 3=cos ^2fracpi 6, значит, заданное уравнение равносильно уравнению cos^2x=cos ^22x, которое, в свою очередь, равносильно уравнению cos^2x-cos ^2 2x=0.

Но cos ^2x-cos ^22x= (cos x-cos 2x)cdot (cos x+cos 2x) и

cos 2x=2 cos ^2 x-1, поэтому уравнение примет вид

(cos x-(2 cos ^2 x-1)),cdot (cos x+(2 cos ^2 x-1))=0,

(2 cos ^2 x-cos x-1),cdot (2 cos ^2 x+cos x-1)=0.

Тогда либо 2 cos ^2 x-cos x-1=0, либо 2 cos ^2 x+cos x-1=0.

Решая первое уравнение как квадратное уравнение относительно cos x, получаем:

(cos x)_=frac4=frac4. Поэтому либо cos x=1, либо cos x=-frac12. Если cos x=1, то x=2kpi , k in mathbb Z. Если cos x=-frac12, то x=pm frac3+2spi , s in mathbb Z.

Аналогично, решая второе уравнение, получаем либо cos x=-1, либо cos x=frac12. Если cos x=-1, то корни x=pi +2mpi , m in mathbb Z. Если cos x=frac12, то x=pm fracpi 3+2npi , n in mathbb Z.

Объединим полученные решения:

x=mpi , m in mathbb Z; x=pm fracpi 3 +spi , s in mathbb Z.

б) Выберем корни, которые попали в заданный промежуток, с помощью числовой окружности.

Получим: x_1 =frac3, x_2=4pi , x_3 =frac3.

Ответ

а) mpi, m in mathbb Z; pm fracpi 3 +spi , s in mathbb Z;

б) frac3, 4pi , frac3.

Видео:Тригонометрическая окружность. Задание 13 | Математика ЕГЭ | УмскулСкачать

Задание №1176

Условие

а) Решите уравнение 10cos ^2frac x2=frac<11+5ctgleft( dfrac2-xright) >.

б) Укажите корни этого уравнения, принадлежащие интервалу left( -2pi ; -frac2right).

Решение

а) 1. Согласно формуле приведения, ctgleft( frac2-xright) =tgx. Областью определения уравнения будут такие значения x , что cos x neq 0 и tg x neq -1. Преобразуем уравнение, пользуясь формулой косинуса двойного угла 2 cos ^2 frac x2=1+cos x. Получим уравнение: 5(1+cos x) =frac.

Заметим, что frac= frac= 5+frac, поэтому уравнение принимает вид: 5+5 cos x=5 +frac. Отсюда cos x =frac, cos x+sin x =frac65.

2. Преобразуем sin x+cos x по формуле приведения и формуле суммы косинусов: sin x=cos left(fracpi 2-xright), cos x+sin x= cos x+cos left(fracpi 2-xright)= 2cos fracpi 4cos left(x-fracpi 4right)= sqrt 2cos left( x-fracpi 4right) = frac65.

Отсюда cos left(x-fracpi 4right) =frac5. Значит, x-fracpi 4= arccos frac5+2pi k, k in mathbb Z,

или x-fracpi 4= -arccos frac5+2pi t, t in mathbb Z.

Поэтому x=fracpi 4+arccos frac5+2pi k,k in mathbb Z,

или x =fracpi 4-arccos frac5+2pi t,t in mathbb Z.

Найденные значения x принадлежат области определения.

б) Выясним сначала куда попадают корни уравнения при k=0 и t=0. Это будут соответственно числа a=fracpi 4+arccos frac5 и b=fracpi 4-arccos frac5.

1. Докажем вспомогательное неравенство:

Заметим также, что left( frac5right) ^2=frac значит frac5

2. Из неравенств (1) по свойству арккосинуса получаем:

Отсюда fracpi 4+0

Аналогично, -fracpi 4

0=fracpi 4-fracpi 4 fracpi 4

При k=-1 и t=-1 получаем корни уравнения a-2pi и b-2pi.

Bigg( a-2pi =-frac74pi +arccos frac5,, b-2pi =-frac74pi -arccos frac5Bigg). При этом -2pi

-2pi Значит, эти корни принадлежат заданному промежутку left( -2pi , -frac2right).

При остальных значениях k и t корни уравнения не принадлежат заданному промежутку.

Действительно, если kgeqslant 1 и tgeqslant 1, то корни больше 2pi. Если kleqslant -2 и tleqslant -2, то корни меньше -frac2.

Ответ

а) fracpi4pm arccosfrac5+2pi k, kinmathbb Z;

б) -frac4pm arccosfrac5.

Видео:Прокачиваем тригонометрию. Задача 13 профильный ЕГЭ, Ященко 2021Скачать

Задание №1175

Условие

а) Решите уравнение sin left( fracpi 2+xright) =sin (-2x).

б) Найдите все корни этого уравнения, принадлежащие промежутку [0; pi ];

Решение

а) Преобразуем уравнение:

cos x+2 sin x cos x=0,

x =fracpi 2+pi n, n in mathbb Z;

x=(-1)^cdot fracpi 6+pi k, k in mathbb Z.

б) Корни, принадлежащие отрезку [0; pi ], найдём с помощью единичной окружности.

Указанному промежутку принадлежит единственное число fracpi 2.

Ответ

а) fracpi 2+pi n, n in mathbb Z; (-1)^cdot fracpi 6+pi k, k in mathbb Z;

б) fracpi 2.

Видео:Сложные уравнения №13 | ЕГЭ по математике | Аня МатеманяСкачать

Задание №1174

Условие

б) Найдите все корни этого уравнения, принадлежащие отрезку left[ -frac; -frac2 right].

Решение

а) Найдём ОДЗ уравнения: cos 2x neq -1, cos (pi +x) neq -1; Отсюда ОДЗ: x neq frac pi 2+pi k,

k in mathbb Z, x neq 2pi n, n in mathbb Z. Заметим, что при sin x=1, x=frac pi 2+2pi k, k in mathbb Z.

Полученное множество значений x не входит в ОДЗ.

Значит, sin x neq 1.

Разделим обе части уравнения на множитель (sin x-1), отличный от нуля. Получим уравнение frac 1=frac 1, или уравнение 1+cos 2x=1+cos (pi +x). Применяя в левой части формулу понижения степени, а в правой — формулу приведения, получим уравнение 2 cos ^2 x=1-cos x. Это уравнение с помощью замены cos x=t, где -1 leqslant t leqslant 1 сводим к квадратному: 2t^2+t-1=0, корни которого t_1=-1 и t_2=frac12. Возвращаясь к переменной x , получим cos x = frac12 или cos x=-1, откуда x=frac pi 3+2pi m, m in mathbb Z, x=-frac pi 3+2pi n, n in mathbb Z, x=pi +2pi k, k in mathbb Z.

б) Решим неравенства

1) -frac2 leqslant frac3+2pi m leqslant -frac pi 2 ,

2) -frac2 leqslant -frac pi 3+2pi n leqslant -frac pi

3) -frac2 leqslant pi+2pi k leqslant -frac pi 2 , m, n, k in mathbb Z.

1) -frac2 leqslant frac3+2pi m leqslant -frac pi 2 , -frac32 leqslant frac13+2m leqslant -frac12 -frac6 leqslant 2m leqslant -frac56 , -frac leqslant m leqslant -frac5.

Нет целых чисел, принадлежащих промежутку left [-frac;-frac5right] .

2) -frac 2 leqslant -frac3+2pi n leqslant -frac, -frac32 leqslant -frac13 +2n leqslant -frac12 , -frac76 leqslant 2n leqslant -frac1, -frac7 leqslant n leqslant -frac1.

Нет целых чисел, принадлежащих промежутку left[ -frac7 ; -frac1 right].

3) -frac2 leqslant pi +2pi kleqslant -frac2, -frac32 leqslant 1+2kleqslant -frac12, -frac52 leqslant 2k leqslant -frac32, -frac54 leqslant k leqslant -frac34.

Этому неравенству удовлетворяет k=-1, тогда x=-pi.

Ответ

а) frac pi 3+2pi m; -frac pi 3+2pi n; pi +2pi k, m, n, k in mathbb Z;

🌟 Видео

Отбор корней с аркфункциями в №12 | Это будет на ЕГЭ 2023 по математикеСкачать

Тригонометрические уравнения. Задание 12 | Профильная математика ЕГЭ 2023 | УмскулСкачать

13 задание ЕГЭ по ПРОФИЛЬНОЙ математике за 6 минутСкачать

3,5 способа отбора корней в тригонометрии | ЕГЭ по математике | Эйджей из ВебиумаСкачать

Тригонометрия | Задача №13 | ЕГЭ по профильной математике | Аня Матеманя | ТопскулСкачать

ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ егэ по математике 13 заданиеСкачать

Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

РАЗБОР 13 ЗАДАНИЯ ЕГЭ МАТЕМАТИКА ПРОФИЛЬ ЗА 30 СЕКУНД!?Скачать

Задание 13 ЕГЭ ПрофильСкачать

Задание №13. Как отбирать корни в тригонометрической окружности? 🤔Скачать

ЕГЭ-ПРОФИЛЬ. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ. ЗАДАНИЕ-12Скачать