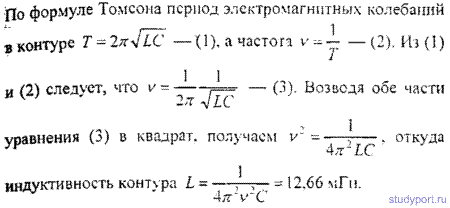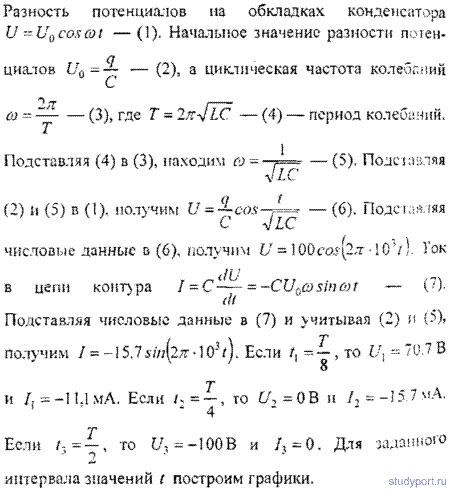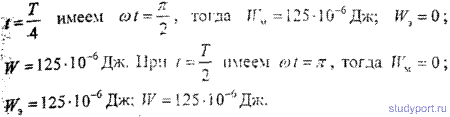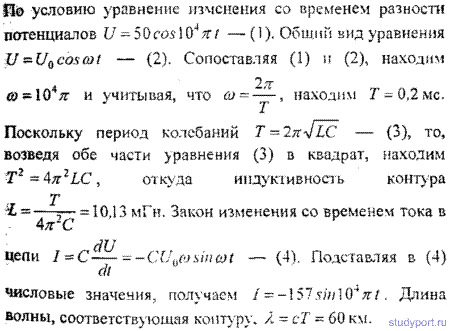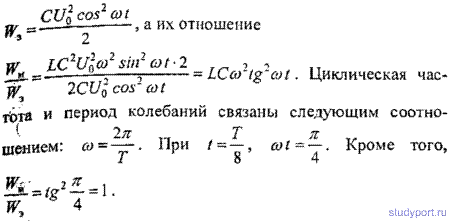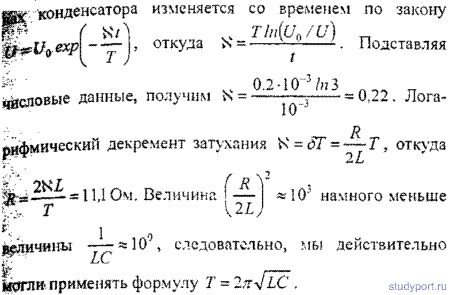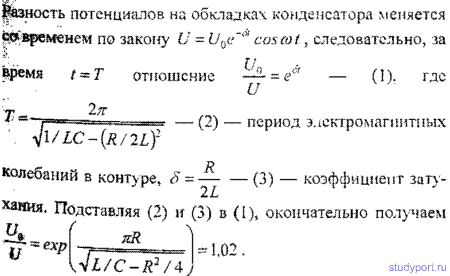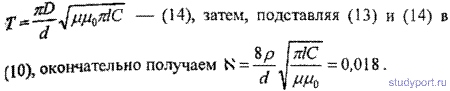Зная уравнение изменения со временем разности потенциалов на обкладках конденсатора u 50cos10 (8 видео)

Зная уравнение изменения со временем разности потенциалов на обкладках конденсатора u 50cos10

Электромагнитные колебания и волны

Уравнение изменения со временем разности потенциалов на обкладках конденсатора в колебательном контуре имеет вид U = 50cos 10 4 πt В. Емкость конденсатора С = 0,1 мкФ. Найти период T колебаний, индуктивность L контура, закон изменения со временем t тока I в цепи и длину волны λ, соответствующую этому контуру.

Дано:

U = 50cos 10 4 πt В

q = 2,5 мкКл = 2,5·10 -6 Кл

Решение:

Закон изменения напряжения на обкладках конденсатора

Период колебаний находим по формуле Томсона

Циклическая частота связана с периодом соотношением

Уравнение колебания напряжения запишется в виде

Тогда период колебаний

Амплитуда заряда на обкладках конденсатора

Аналогично можно записать уравнение изменения заряда на обкладках конденсатора

Ток в контуре – первая производная от заряда по времени

Видео:Комбинаторика: перестановка, размещение и сочетание | Математика | TutorOnlineСкачать

Электромагнитные колебания и волны

14.1. Колебательный контур состоит из конденсатора емкостью С = 888 пФ и катушки с индуктивностью L = 2 мГн. На какую длину волны λ настроен контур?

14.2. На какой диапазон длин волн можно настроить колебательный контур, если его индуктивность L = 2мГн, а емкость может меняться от С₁ = 69 пФ до С₂ = 533 пФ?

14.3. Какую индуктивность L надо включить в колебательный контур, чтобы при емкости С = 2 мкФ получить частоту v = 1000 Гц?

14.4. Катушка с индуктивностью L = 30 мкГн присоединена к плоскому конденсатору с площадью пластин S = 0,01.м 2 и расстоянием между ними d = 0,1 мм. Найти диэлектрическую проницаемость ε среды, заполняющей пространство между пластинами, если контур настроен на длину волны λ = 750 м.

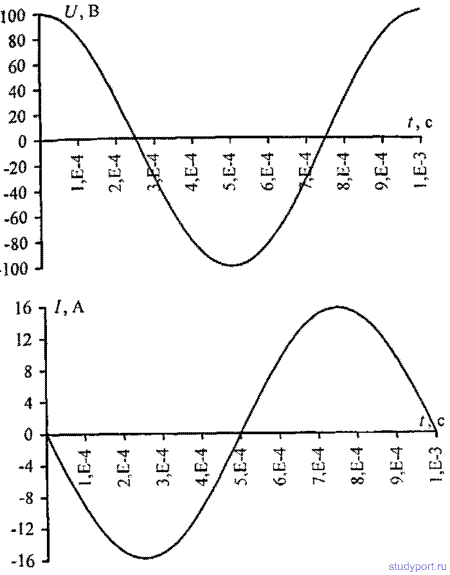
14.5. Колебательный контур состоит из конденсатора емкостью С = 25нФ и катушки с индуктивностью L = 1,015Гн. Обкладки конденсатора имеют заряд q = 2,5мкКл. Написать уравнение (с числовыми коэффициентами) изменения разности потенциалов U на обкладках конденсатора и тока I в цепи. Найти разность потенциалов на обкладках конденсатора и ток в цепи в моменты времени T/8, Т/4 и Т/2. Построить графики этих зависимостей в пределах одного периода.

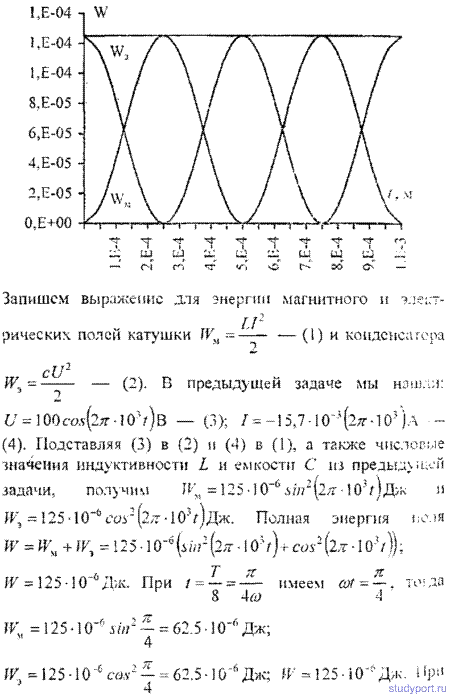
14.6. Для колебательного контура предыдущей задачи написать уравнение (с числовыми коэффициентами) изменения со временем t энергии электрического поля W_Э, энергии магнитного поля W_M и полной энергии поля W . Найти энергию электрического поля, энергию магнитного поля и полную энергию поля в моменты времени T/8, T/4 и T/2. Построить графики этих зависимостей в пределах одного периода.

14.7. Уравнение изменения со временем разности потенциалов на обкладках конденсатора в колебательном контуре имеет вид U = 50cos*10 4 πt. В. Емкость конденсатора С = 0,1мкФ. Найти период Т колебаний, индуктивность L контура, закон изменения со временем t тока I в цепи и длину волны λ, соответствующую этому контуру.

14.8. Уравнение изменения со временем тока в колебательном контуре имеет вид I = -0.02*sin400πt А. Индуктивность контура L = 1Гн. Найти период Т колебаний, емкость С контура, максимальную энергию W_м магнитного поля и максимальную энергию W_эл электрического поля.

14.9. Найти отношение энергии W_м/W_эл магнитного поля колебательного контура к энергии его электрического поля для момента времени T/8.

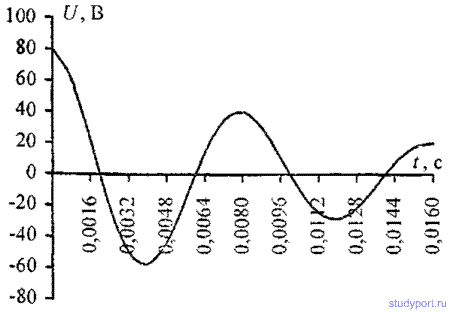
14.10. Колебательный контур состоит из конденсатора емкостью С = 7мкФ и катушки с индуктивностью L = 0,23Гн и сопротивлением R = 40 Ом. Обкладки конденсатора имеют заряд q = 0,56 мКл. Найти период Т колебаний контура и логарифмический декремент затухания N колебаний. Написать уравнение изменения со временем t разности потенциалов U на обкладках конденсатора. Найти разность потенциалов в моменты времени, равные: T/2, T и 2T. Построить график U = f(t) в пределах двух периодов.

14.11. Колебательный контур состоит из конденсатора емкостью С=0,2мкФ н катушки с индуктивностью L = 5,07 мГи. При каком логарифмическом декременте затухания N разность потенциалов на обкладках конденсатора за время t = 1мс уменьшится в три раза? Каково при этом сопротивление R контура?

14.12. Колебательный контур состоит из конденсатора емкостью С = 405нФ, катушки с индуктивностью L = 10мГн и сопротивления R=2 Ом. Во сколько раз уменьшится разность потенциалов на обкладках конденсатора за один период колебаний.

14.13. Колебательный контур состоит из конденсатора емкостью С = 2,22 нФ и катушки длиной l = 20 см из медной проволоки диаметром d = 0,5 мм. Найти логарифмический декремент затухания N колебаний.

14.14. Колебательный контур имеет емкость С = 1,1 нФ и индуктивность L = 5 мГн. Логарифмический декремент затухания N = 0,005. За какое время вследствие затухания потеряется 99% энергии контура?

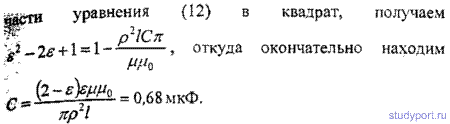
14.15. Колебательный контур состоит из конденсатора и катушки длиной l = 40 см из медной проволоки, площадь поперечного сечения которой s = 0,1 мм 2 . Найти емкость конденсатора С , если, вычисляя период колебаний контура по приближенной, формуле Т = 2π√(LC), мы допускаем ошибку ε = 1%.

Указание: учесть, что ошибка ε =T2-T1/T2,где Т1 — период колебаний, найденный по приближенной формуле, а T2 — период колебаний, найденный по точной формуле.

14.16. Катушка длиной l = 50 см и площадью поперечного сечения S = 10cm 2 включена в цепь переменного тока частотой ν = 50Гц. Число витков катушки N = 3000. Найти сопротивление R катушки, если сдвиг фаз между напряжением и током φ = 60°.

14.17. Обмотка катушки состоит из N = 500 витков медной проволоки, площадь поперечного сечения которой s = 1 мм 2 .Длина катушки l = 50 см, ее диаметр D = 5 см. При какой частоте v переменного тока полное сопротивление Z катушки вдвое больше ее активного сопротивления R?

14.18. Два конденсатора с емкостями С₁ = 0,2мкФ и С₂ = 0,1мкФ включены последовательно в цепь переменного тока напряжением U = 220 В и частотой v = 50 Гц. Найти ток Iв цепи и падения потенциала U_C1 и U_C2 на первом и втором конденсаторах.

14.19. Катушка длиной l = 25 см и радиусом r = 2 см имеет обмотку из N = 1000 витков медной проволоки, площадь Поперечного сечения которой s = 1 мм 2 . Катушка включена в цепь переменного тока частотой v = 50 Гц. Какую часть полного сопротивления Z катушки составляет активное сопротивление R и индуктивное сопротивление X_L?

14.20. Конденсатор емкостью С = 20мкФ и резистор, сопротивление которого R = 150 Ом, включены последовательно в цепь переменного тока частотой v = 50 Гц. Какую часть напряжения U, приложенного к этой цепи, составляют падения напряжения на конденсаторе U_C и на резисторе U_R ?

Ошибка в тексте? Выдели её мышкой и нажми

Остались рефераты, курсовые, презентации? Поделись с нами — загрузи их здесь!

Видео:Количество теплоты, удельная теплоемкость вещества. 8 класс.Скачать

Индивидуальные задания из задачника

Индивидуальные задания из задачника

, , Физика: Сборник задач (с решениями). Часть 2. Электричество и магнетизм: Учебное пособие. – Томск: Изд-во Том. ун-та, 2004. – 448 с.

КОЛЕБАНИЯ И ВОЛНЫ

1. СВОБОДНЫЕ (ГАРМОНИЧЕСКИЕ) И ЗАТУХАЮЩИЕ КОЛЕБАНИЯ

1.1. Записать уравнение гармонических колебаний при следующих параметрах:

А = 10 см; j0 = p/4 рад; w = 2p рад/с.

А = 5,0 см; j0 = p/4 рад; Т = 2 с.

А = 4,0 см; j0 = p рад; n = 2,0 с-1.

1.2. Материальная точка совершает гармонические колебания по закону где х – в см; t – в с. Определите амплитуду колебаний А, начальную фазу j0, период колебаний Т.

Ответ: А = 2 см; j0 = p/2; Т = 8 с.

1.3. Амплитуда гармонических колебаний материальной точки А = 2 см, полная энергия колебаний W = 3×10-7 Дж. При каком смещении от положения равновесия на колеблющуюся точку действует сила F = 2,25×10-5Н?

Ответ: х = 1,5×10-2 м.

1.4. Уравнение колебания материальной точки массой т = 1,6×10-2 кг имеет вид x = 0,1м. Построить график зависимости от времени t (в пределах одного периода) силы F, действующей на точку. Найти значение максимальной силы.

Ответ: Fmax = 24,6×10-2 Н.

1.5. Начальная фаза гармонического колебания равна нулю. При смещении точки от положения равновесия, равном 2,4 см, скорость точки равна 3 см/с, а при смещении, равном 2,8 см, скорость равна 2 см/с. Найти амплитуду и период этого колебания.

Ответ: А = 3,1×10-2м; Т = 4,1 с.

1.6. Написать уравнение гармонического колебательного движения, если максимальное ускорение точки 49,3 см/с2, период колебания 2 с и смещение точки от положения равновесия в начальный момент времени 25 мм.

1.7. Точка совершает гармонические колебания. В некоторый момент времени смещение точки равняется 5 см, скорость ее υ = 20 см/с и ускорение а = -80 см/с2. Найти: циклическую частоту и период колебаний, фазу колебаний в рассматриваемый момент времени и амплитуду колебаний.

Ответ: 4 с-1; 1,57 с; π/4; 7,07 см.

1.8. Математический маятник длиной 1 м установлен в лифте. Лифт поднимается с ускорением 2,5 м/с2. Определить период колебания маятника.

1.9. Математический маятник длиной 50 см колеблется в кабине самолета. Каков период его колебаний, если самолет: а) движется равномерно; б) летит горизонтально с ускорением 2,5 м/с2; в) планирует вниз под углом 15 ° к горизонту?

Ответ: Т1 = 1,42 с; Т2 = 1,4 с; Т3 = 1,44 с.

1.10. За две минуты маятник совершил 120 колебаний. Когда длину маятника увеличили на 74,7 см, то он за то же время совершил 60 колебаний. Найти начальную и конечную длину маятника и ускорение свободного падения в этом месте.

1.11. Найти амплитуду А, период Т, частоту n и начальную фазу j0 колебания, заданного уравнением см.

Ответ: А = 5 см; n = 1,25 Гц; Т = 0,8 с; j0 = 1,04 рад.

1.12. Как изменится период колебаний маятника при переносе его с Земли на Луну?

1.13. Однородный диск радиуса R колеблется около горизонтальной оси, проходящей через одну из образующих цилиндрической поверхности диска. Каков период его колебаний?

Ответ:

1.14. К пружине подвешена чашка весов с гирями. Период вертикальных колебаний чашки равен Т1. После того как на чашку положили добавочные гири, период вертикальных колебаний стал равен Т2. На сколько удлинилась пружина от прибавления добавочного груза?

Ответ:

1.15. Частота электрических колебаний в контуре оказалась 1,0 МГц. Емкость конденсатора 200 пФ. Какова индуктивность катушки?

1.16. Колебательный контур состоит из конденсатора емкостью 2,0 пФ и катушки с индуктивностью 0,50 мкГн. Какова частота колебаний в контуре?

1.17. В колебательном контуре происходят свободные колебания. Зная, что максимальный заряд конденсатора равен 10-6 Кл, а максимальный ток 10 А, найти длину волны этого контура.

1.18. Катушка, индуктивность которой L = 3×10-5 Гн, присоединена к плоскому конденсатору с площадью пластин S = 100 см2. Расстояние между пластинами d = 0,1 мм. Чему равна относительная диэлектрическая проницаемость среды между пластинами конденсатора, если контур резонирует на волну длиной l = 750 м?

1.19. Какую индуктивность надо включить в колебательный контур, чтобы при емкости С = 2 мкФ получить звуковую частоту n = 103 Гц? Сопротивлением контура пренебречь.

Ответ: L = 12,7×10-3 Гн.

1.20. Уравнение изменения со временем разности потенциалов на обкладках конденсатора в колебательном контуре дано в виде U = 50 cos 104 pt В. Емкость конденсатора равна 10-7 Ф. Найти: 1) период колебаний; 2) индуктивность контура; 3) закон изменения со временем силы тока в цепи; 4) длину волны, соответствующую этому контуру.

Ответ: Т = 2×10-4 с; L = 10,15 мкГн; I = -157 sin 104 pt мА;

1.21. Уравнение изменения силы тока в колебательном контуре со временем дается в виде I = -0,02 sin 400 pt А. Индуктивность контура 1 Гн. Найти: 1) период колебаний; 2) емкость контура; 3) максимальную разность потенциалов на обкладках конденсатора; 4) максимальную энергию магнитного поля; 5) максимальную энергию электрического поля.

Ответ: Т = 5×10-3 с; С = 6,3×10-7 Ф; Umax = 25,2 В;

Wmax = 2×10-4 Дж; Wэл = 2×10-4 Дж.

1.22. Чему равно отношение энергии магнитного поля колебательного контура к энергии его электрического поля для момента времени Т/8 с?

1.23. Колебательный контур состоит из индуктивности и двух одинаковых конденсаторов, включенных параллельно. Период колебания контура Т1 = 20 мкс. Чему будет равен период, если конденсаторы включить последовательно?

Ответ: Т2 = 10 мкс.

1.24. Колебательный контур состоит из катушки индуктивностью L = 1 мГн и воздушного конденсатора, обкладка которого – две круглые пластины диаметром D = 20 см каждая. Расстояние между пластинами d = 1 см. Определите период колебательного контура. Электрическая постоянная e0 = 8,85×10-12 Ф/м.

Ответ: Т = 1,06×10-6 с.

1.25. Максимальный заряд на обкладках конденсатора колебательного контура 1×10-6 Кл. Амплитудное значение силы тока в контуре 1×10-3 А. Определить период колебаний.

Ответ: Т = 6,28 мс.

2.1. Математический маятник длиной 0,5 м, выведенный из положения равновесия, отклонился при первом колебании на 5 см, а при втором (в ту же сторону) – на 4 см. Найти время релаксации, т. е. время, в течение которого амплитуда колебаний уменьшится в е раз, где е – основание натуральных логарифмов.

2.2. Уравнение затухающих колебаний дано в виде х = 5е-0,25t sin (p/2) м. Найти скорость колеблющейся точки в моменты времени: 0, Т, 2Т.

Ответ: υ1 = 7,85 м/с; υ 2 = 2,88 м/с; υ 3 = 1,06 м/с.

2.3. Математический маятник длиной 1,2 м колеблется в среде с малым сопротивлением. Считая, что сопротивление среды не влияет на период колебания маятника, найти коэффициент затухания и логарифмический декремент затухания, если за 8 мин амплитуда колебаний маятника уменьшилась в три раза.

Ответ: 10-3 с-1; 5,05×10-3.

2.4. Гиря массой 500 г подвешена к спиральной пружине жесткостью 0,2 Н/см и совершает упругие затухающие колебания. Логарифмический декремент затухания равен 0,004. Сколько колебаний должна совершить гиря, чтобы амплитуда колебаний уменьшилась в два раза? За какой промежуток времени произойдет это уменьшение?

Ответ: N = 173; t = 2 мин 52 с.

2.5. Логарифмический декремент колебаний d маятника равен 0,003. Определить число N полных колебаний, которые должен сделать маятник, чтобы амплитуда уменьшилась в 2 раза.

2.6. Чему равен логарифмический декремент затухания математического маятника, если за 1 мин амплитуда колебаний уменьшилась в два раза? Длина маятника 1 м.

2.7. Тело массой m = 5 г совершает затухающие колебания. В течение времени t = 50 с тело потеряло 60 % своей энергии. Определить коэффициент сопротивления r.

Ответ: r = 9,16×10-5 кг/с.

2.8. Амплитуда затухающих колебаний математического маятника за 60 с увеличилась в 2 раза. Во сколько раз она уменьшится за 180 с?

2.9. К вертикально висящей пружине подвешивают груз. При этом пружина удлиняется на 9,8 см. Оттягивая этот груз и опуская его, заставляют груз совершать колебания. Чему должен быть равен коэффициент затухания d, чтобы колебания прекратились через 10 с (считать условно, что колебания прекратились, если их амплитуда упала до 1 % от начальной)?

2.10. Амплитуда затухающих колебаний математического маятника за 1 мин уменьшилась вдвое. Во сколько раз она уменьшится за 3 мин?

2.11. Период затухающих колебаний 4 с, логарифмический декремент затухания 1,6. Начальная фаза равна нулю. Смещение точки при t = Т/4 = 4,5 см. Написать уравнение движения этого колебания.

Ответ:

2.12. Математический маятник длиной в 24,7 см совершает затухающие колебания. Через сколько времени энергия колебаний маятника уменьшится в 9,4 раза? Задачу решить при значении логарифмического декремента затухания: d = 0,01 и d = 1.

Ответ: 120 с; 1,22 с.

2.13. Математический маятник совершает затухающие колебания с логарифмическим декрементом затухания, равным 0,2. Во сколько раз уменьшится полное ускорение маятника в его крайнем положении за одно колебание?

Ответ: в 1,22 раза.

2.14. Логарифмический декремент затухания системы d = 0,01. Найти число N полных колебаний системы, в течение которых энергия системы уменьшилась в n = 2 раза.

2.15. Период Т0 собственных колебаний системы равен 1 с, а логарифмический декремент d = 0,628. Каков период Т затухающих колебаний системы?

Ответ: Т = 1,005 с.

2.16. К вертикально висящей пружине подвешивают груз. При этом пружина удлиняется на 9,8 см. Оттягивая этот груз вниз и отпуская его, заставляют груз совершать колебания. Чему должен быть равен коэффициент затухания b, чтобы: 1) колебания прекратились через 10 с (считать условно, что колебания прекратились, если амплитуда упала до 1 % от начальной величины); 2) груз возвращался в положение равновесия апериодически; 3) логарифмический декремент затухания был равен 6?

Ответ: 1) b = 0,46 с-1; 2) b = 10 с-1; 3) b = 6,9 с-1.

2.17. Чему равна частота свободных колебаний в контуре, состоящем из емкости 2,2 мкФ, индуктивности 0,12 Гн и активного сопротивления 15 Ом?

Ответ: свободных колебаний в контуре нет.

2.18. Свободные колебания в контуре происходят с частотой 250 кГц. Определить емкость в контуре, если индуктивность в нем равна 0,024 мГн и активное сопротивление равно 34 Ом.

Ответ: С = 1,4×104 пФ.

2.19. Какой длины волны будут создавать в вакууме свободные колебания, которые происходят в контуре с емкостью 2400 пФ, индуктивностью 0,054 мГн и активным сопротивлением 76 Ом?

Ответ: l = 710 см.

2.20. Определить период свободных колебаний в контуре, состоящем из конденсатора емкостью 0,064 мкФ и катушки с индуктивностью 0,18 мГн и активным сопротивлением 50 Ом.

Ответ: Т = 24 мкс.

2.21. Колебательный контур состоит из конденсатора емкостью С = 2,22×10-9 Ф и катушки, намотанной из медной проволоки диаметром d = 0,5 мм. Длина катушки l = 20 см. Найти логарифмический декремент затухания колебаний.

Ответ: , где r — плотность меди.

2.22. Колебательный контур состоит из конденсатора емкостью 0,2 мкФ и катушки индуктивностью 5,07×10-3 Гн. 1) При каком логарифмическом декременте затухания разность потенциалов на обкладках конденсатора за t = 3 с уменьшится в три раза? 2) Чему при этом равно сопротивление контура?

Ответ: d = 0,22; R = 11,1 Ом.

2.23. Колебательный контур имеет емкость 1,1×10-9 Ф и индуктивность 5×10-3 Гн. Логарифмический декремент затухания равен 0,005. За сколько времени потеряется вследствие затухания 99 % энергии контура?

Ответ: с.

2.24. Колебательный контур состоит из емкости С = 0,405 мкФ, индуктивности L = 10-2 Гн и сопротивления R = 2 Ом. Найти, во сколько раз уменьшится разность потенциалов на обкладках конденсатора за время одного периода.

Ответ: в 1,04 раза.

2.25. Параметры некоторого колебательного контура имеют значения: С = 4 мкФ; L = 0,1 мГн; R = 1 Ом. Чему равна добротность контура Q? (Добротность контура при малых значениях логарифмического декремента d Q = p / d).

2. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ. РЕЗОНАНС

1.1. Активное сопротивление колебательного контура R = 0,33 Ом. Какую мощность потребляет контур при поддержании в нем незатухающих колебаний с амплитудой тока Im = 30 мА? Дать развернутый ответ.

1.2. Переменное напряжение, действующее значение которого U = 220 В, а частота n = 50 Гц, подано на катушку без сердечника с индуктивностью L = 31,8 мГн и активным сопротивлением R = 10,0 Ом. Найти количество теплоты Q, выделяющееся в катушке за секунду.

1.3. Колебательный контур состоит из конденсатора емкостью 10 мкФ, катушки с индуктивностью 0,01 Гн и омического сопротивления 4 Ом. Какую мощность должен потреблять контур, чтобы в нем поддерживались незатухающие колебания с амплитудой напряжения 1 В?

1.4. Емкость колебательного контура 1 мкФ, индуктивность 10 мГн. Какое омическое сопротивление нужно включить в цепь, чтобы уменьшить резонансную частоту незатухающих колебаний на 0,01 %.

1.5. Индуктивность, емкость и сопротивление колебательного контура равны соответственно 1,0 Гн, 20 мкФ и 10 Ом. При какой частоте внешней ЭДС будет достигнут максимум резонанса?

1.6. Индуктивность дросселя, включенного последовательно с емкостью, равна 0,05 Гн, его активное сопротивление 100 Ом. В контуре возникает резонанс при частоте nрез = 5000 Гц. Найти полное сопротивление цепи на частоте n1 = 5 кГц.

1.7. Конденсатор емкостью 1 мкФ с зарядом 8×10-5 Кл разряжается на катушку с индуктивностью 1,6 Гн и сопротивлением 40 Ом. Определите закон изменения напряжения на конденсаторе.

Ответ: UC = 80 exp (-12,5t) cos 790t.

1.8. Вычислить амплитуду на конденсаторе приемной антенны телевизора на частоте n = 194 МГц, если E0 входное переменное напряжение 100 мкВ. Емкость конденсатора антенн С = 0,567 пФ, индуктивность L = 1,26 мкГн, ее сопротивление 20 Ом. Резонансная частота nрез = 188 МГц.

Ответ: = 1,54 мВ.

1.9. Найти добротность колебательного контура приемной антенны типичного современного домашнего телевизора (резонансная частота контура nрез = 188 МГц). Сравните эту величину со значением Va0 / E0, где Va0 – амплитудное значение напряжения на конденсаторе при резонансе. Параметры контура: С = 0,567 пФ; R = 20 Ом; L = 1,26 мкГн.

1.10. Емкость и индуктивность колебательного контура равны 20 мкФ и 1 Гн. Каково активное сопротивление контура, если максимум резонанса наблюдается при n = 223 Гц?

1.11. Колебательный контур состоит из катушки индуктивности L = 0,002 Гн, активного сопротивления R = 10 Ом и конденсатора С = 4 мкФ. Найти отношение энергии электрического поля конденсатора в момент максимума тока к энергии магнитного поля катушки.

Ответ:

1.12. Найти время t, за которое амплитуда колебаний тока в контуре с добротностью Q = 5000 уменьшится в g = 2 раза, если частота колебаний n = 2,0 МГц.

Ответ: 0,55 с.

1.13. Дроссель и конденсатор включены последовательно. В контуре возникает резонанс при частоте 6 кГц. Найти полное сопротивление цепи на частоте n = 6000 Гц, если L = 0,005 Гн, R = 100 Ом.

1.14. Конденсатор емкостью 1 мкФ и катушку L = 0,001 Гн и активное сопротивление R = 0,1 Ом подключили к источнику синусоидального напряжения с U0 = 31 В. Найти частоту, при которой наступает резонанс.

Ответ: рад/с.

1.15. Найти полное сопротивление участка цепи, состоящей из параллельно включенного конденсатора емкости С = 73 мкФ и активного сопротивления R = 100 Ом, если частота тока в цепи w = 314 рад/с.

1.16. Какая нужна вынуждающая сила, чтобы осциллятор массы m с коэффициентом затухания b начал совершать гармонические колебания с собственной частотой w0 по закону х = Аcos(w0t – j)?

Ответ: F = -2bw0 sin(w0t – j).

1.17. Амплитуда вынуждающей силы равна F0, ее частота w = w0. Определите амплитуду вынужденных колебаний. Во сколько раз она больше отклонения осциллятора при действии постоянной силы F0?

Ответ: А = —F0 / 2bm0w0; (w0 / 2b) раз.

1.18. Осциллятор движется по закону F = F0 cos w0t. Каков коэффициент затухания у осциллятора? Масса осциллятора m.

1.19. Игла звукоснимателя движется по синусоидальной бороздке грампластинки. Частота собственных колебаний иглы w0. При какой скорости иглы относительно пластинки она начнет выскакивать из бороздки? Изгибы бороздки повторяются через расстояние l.

1.20. Найти зависимость координаты осциллятора от времени, если w ® w0.

Ответ:

1.21. С момента времени t = 0 на частицу массы m начинает в направлении оси х действовать сила Fх = F0 sin w0t, а в направлении у – сила Fх = Fy cos w0t. Найти траекторию частицы, если в начальный момент она покоится. Чему равна средняя скорость частицы за большое время?

1.22. По условию задачи 23.18. найдите: а) какую начальную скорость должна иметь частица, чтобы двигаться при наличии сил Fx и Fy по окружности? б) каков радиус этой окружности?

1.23. Тело совершает вынужденные колебания в среде с коэффициентом сопротивления r = 1 г/с. Считая затухание малым, определить амплитудное значение вынуждающей силы, если резонансная амплитуда Арез = 0,5 см и частота n0 собственных колебаний равна 10 Гц.

Ответ: F0 = 0,314 мН.

1.24. В момент времени t0 на покоящийся в положении равновесия осциллятор начинает действовать вынуждающая сила F = F0 cos w0t. Масса осциллятора m, его собственная частота w0. Найдите зависимость координаты осциллятора от времени и постройте ее график для |w — w0|. При построении графика воспользуйтесь тождеством

Ответ: x(t) =

1.25. Частицы массой m каждая вылетают из источника в момент времени t = 0 с почти нулевой скоростью. Сразу после вылета на них начинает действовать сила F = F0 sin w0t. Определите скорость частиц спустя время t после вылета. Какова средняя скорость этих частиц? На каком расстоянии l от источника достигается наибольшая скорость?

Ответ:

где n – целое число.

3. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ

1.1. В вакууме распространяется плоская электромагнитная волна Е = Ем cos(wt – kr) j, где j – орт оси y; Ем = 100 В/м, k = 0,5 м-1. Найти вектор Н в точке с координатой x = 5,0 м в моменты времени t = 0, t = 50 нс.

1.2. При переходе электромагнитной волны из немагнитной среды с диэлектрической проницаемостью e = 2 в вакуум изменение длины волны Dl = 17,6 м. Найти частоту n электромагнитной волны.

Ответ. n= = 5 МГц.

1.3. При изменении тока в катушке индуктивности на величину I = 1 А за время t = 0,6 с в ней индуцируется ЭДС, равная ei = 0,2 мВ. Какую длину будет иметь радиоволна, излучаемая генератором, колебательный контур которого состоит из этой катушки и конденсатора емкостью C = 14,1 нФ?

1.4. Катушка, индуктивность L которой 30 мкГн, присоединена к плоскому конденсатору. Площадь S каждой пластины 100 см2, расстояние d между ними 0,1 мм. Определить диэлектрическую проницаемость среды, заполняющей пространство между пластинами, если контур резонирует на электромагнитную волну длиной l = 750 м.

1.5. В вакууме вдоль оси x распространяется плоская электромагнитная волна. Амплитуда напряженности электрического поля волны равна 10 В/м. Определить амплитуду напряженности магнитного поля волны.

Ответ: Hm =Em = 0,0265 А/м.

1.6. Тонкая катушка, имеющая вид кольца радиусом R = 25 см, состоит из n витков провода. Катушка находится в поле электромагнитной волны частотой n = 5,0 МГц, направление распространения которой и ее электрический вектор перпендикулярны оси катушки. Чему равно амплитудное значение электрического вектора волны Em, если амплитудное значение ЭДС индукции в катушке равно eim = 0,2 мВ?

Ответ: Em == 192 мкВ/м.

1.7. В некоторой области инерциальной системы отсчета имеется вращающееся с угловой скоростью ω магнитное поле, модуль которого |В| = const. Найти rot Е в этой области как функцию векторов w и B.

1.8. В вакууме вдоль оси x распространяется плоская электромагнитная волна и падает по нормали на поверхность тела, полностью ее поглощающего. Амплитуда напряженности электрического поля волны равна 2 В/м. Определить давление, оказываемое волной на тело.

1.9. Плоская гармоническая линейно поляризованная электромагнитная волна c частотой n = 1 МГц распространяется в вакууме. Найти амплитуду напряженности электрической составляющей, если интенсивность I электромагнитной волны равна 3 мкВт/м2.

Ответ: == 47,5 мВ/м.

1.10. Найти модуль напряженности магнитного поля плоской электромагнитной волны, выразив его через модуль вектора Пойнтинга S = 3 мкВт/м2, и диэлектрическую проницаемость e среды. Принять m = 1, e = 4.

Ответ: Hм = = 22,4 мА/м.

1.11. Найти интенсивность плоской электромагнитной волны, электрическая составляющая которой Е = Ем cos (wt – kr), если волна распространяется в вакууме. Ответ выразить через k и w.

Ответ: I =.

1.12. По медному проводу диаметром d = 2,5 мм с сопротивлением 1 Ом на каждые 305 м течет ток 25 A. Найти модули амплитуд напряженности электрического поля, магнитной индукции и вектора Пойнтинга.

Ответ: Eм = 0,082 В/м; Bм = 3,2×103 Тл; S = 262 Дж/(м2×с).

1.13. В вакууме распространяются две плоские электромагнитные волны, одна – вдоль оси X, другая – вдоль оси Y: Е1 = = Е0 cos (wt – kx), Е2 = Е0 cos (wt – ky), где вектор E0 = 200 В/м параллелен оси Z. Найти среднее значение плотности потока энергии в точках плоскости x = y.

Ответ: = 149 Дж/(м2с).

1.14. Найти время прохождения электромагнитной плоской монохроматической волны, распространяющейся вдоль оси x, если энергия, перенесенная волной через поверхность площадью S = 30 cм2, расположенную перпендикулярно оси x, равна 18 мкДж. Амплитуда напряженности магнитного поля волны Eм = 10 мВ/м, амплитуда напряженности магнитного поля волны Hм = 1 мА/м. Период волны T = t.

Ответ: t == 20 мин.

1.15. Плотность G импульса электромагнитной волны, распространяющейся в вакууме, связана с вектором Пойнтинга S соотношением G = S / c2, где c – скорость распространения электромагнитных волн в вакууме. Используя это соотношение, выразите модуль плотности импульса электромагнитной волны через объемную плотность x энергии электромагнитного поля и скорость распространения электромагнитных волн в вакууме.

1.16. Ток, протекающий по обмотке длинного прямого соленоида, достаточно медленно увеличивают. Показать, что скорость возрастания энергии магнитного поля в соленоиде равна потоку вектора Пойнтинга через его боковую поверхность.

1.17. Энергия от источника постоянного напряжения U = 100 В передается к потребителю по длинному коаксиальному кабелю с пренебрежимо малым сопротивлением. Ток в кабеле I = 10 А. Найти поток энергии через поперечное сечение кабеля. Считать внешнюю проводящую оболочку кабеля тонкостенной.

Ответ: Ф = IU = 1000 Дж/с.

1.18. Известно, что в волновой зоне вибратора Герца (дипольный излучатель), то есть на расстояниях, много больших длины его волны, амплитуды колебаний Ем и Нм прямо пропорциональны синусу угла q между направлением распространения волны и осью вибратора и обратно пропорциональны расстоянию r от вибратора. Найти отношение мощностей, излучаемых диполем в направлениях (30 °