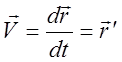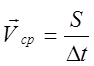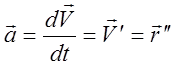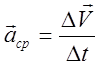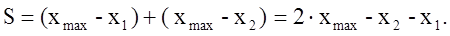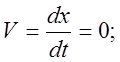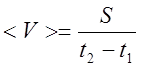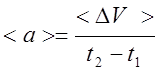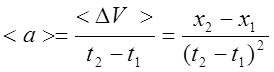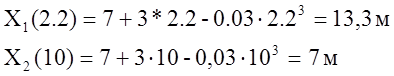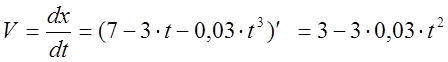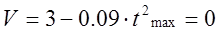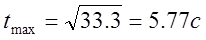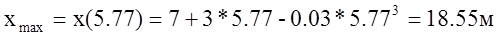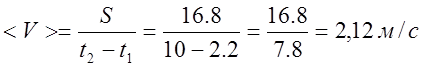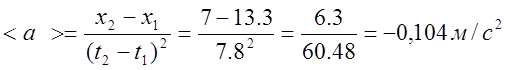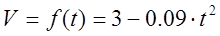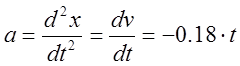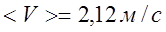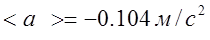Движение материальной точки в пространстве – это изменение ее положения относительно других тел с течением времени.
Имеет смысл говорить только о движении в некоторой системе отсчета.
- Система отсчета. Системы координат
- Кинематическое уравнение движения материальной точки
- Кинематическое уравнение движения материальной точки для координаты имеет вид х = (8 + 3t + 5t^2) м. Определите координату и скорость
- Ваш ответ
- решение вопроса
- Похожие вопросы
- Кинематика материальной точки. Кинематическое уравнение движения материальной точки по прямой
- Страницы работы
- Содержание работы
- Основные определения
- 📹 Видео
Видео:Уравнение движения тела дано в виде x=2−3t. ВычислиСкачать

Система отсчета. Системы координат
Точки, располагаемые в пустом пространстве, не различаются. Поэтому о точке рассуждают при условии нахождения в ней материальной точки. Определить ее положение можно при помощи измерений в системе координат, где и проводится нахождение пространственных координат. Если рассматривать в виде примера поверхность Земли, то следует учитывать широту и долготу располагаемой точки.
В теории используется декартова прямоугольная система координат, где определение точки возможно при наличии радиус-вектора r и трех проекций x , y , z – ее координат. Могут быть применены другие:
- сферическая система с положением точек и ее радиус-вектором, определенных координатами r , υ , φ ;
- цилиндрическая система с координатами p , z , α ;
- на полярной плоскости с параметрами r , φ .
В теории зачастую не принимают во внимание реальную систему отсчета, а сохраняют только ту, которая представляет собой ее математическую модель, применяемую во время практических измерений.
Видео:Задача на движение материальной точки - bezbotvyСкачать

Кинематическое уравнение движения материальной точки
Любая система отсчета или координат предполагает определение координат материальной точки в любой момент времени.
При условии положения и определения материальной точки в данной системе отсчета считается, что ее движение задано или описано.
Это возможно при использовании кинематического уравнения движения:
Аналитически положение точки определяется совокупностью трех независимых между собой чисел. Иначе говоря, свободная точка имеет три степени свободы движения.
Ее перемещение по уравнению ( 1 ) определено, если имеется указанное положение в любой момент времени t . Для этого следует задавать декартовы координаты точки в качестве однозначных и непрерывных функций времени:
x ( t ) = x , y ( t ) = y , z ( t ) = z ( 2 ) .
Прямоугольные декартовы координаты x , y , z — это проекции радиус-вектора r ¯ , проведенного из начала координат. Очевидно, что длину и направление r ¯ можно найти из соотношений, где a , β , γ являются образованными радиус-вектором углами с координатными осями.
Равенства ( 2 ) считают кинематическими уравнениями движения материальной точки в декартовых координатах.
Они могут быть записаны в другой системе координат, которая связана с декартовой взаимно однозначным преобразованием. Если движение точки происходит в плоскости О х у , тогда применимы полярные координаты r , φ , относящиеся к декартовым преобразованиям. Данный случай подразумевает использование уравнения движения точки следующего вида:
r = r ( t ) , φ = φ ( t ) ( 3 ) .
Кинематическое уравнение движения точки в криволинейных координатах q 1 , q 2 , q 3 , связанных с декартовыми преобразованиями вида x = x ( q 1 , q 2 , q 3 ) , y = y ( q 1 , q 2 , q 3 ) , z = z ( q 1 , q 2 , q 3 ) ( 4 ) , записывается как
q 1 = q 1 ( t ) , q 2 = q 2 ( t ) , q 3 = q 3 ( t ) ( 5 ) .
Кривая радиус-вектора, описываемая концом вектора r при движении точки, совпадает с ее траекторией. Параметрическое уравнение траектории с t представлено кинематическими уравнениями ( 2 ) , ( 5 ) . Чтобы получить координатное уравнение траектории следует исключить время из кинематических уравнений.
Определение движения точки возможно с помощью задания траектории и мгновенного положения точки на ней. Ее положение на кривой определяется с помощью указания только одной величины: расстояния вдоль кривой от некоторой начальной точки с положительным направлением:
Это и есть уравнение движения точки по траектории. Способ его задания относят к естественному или траекторному.
Понятия координатного и естественного способа задания движения точки физически эквивалентны. С математической стороны это рассматривают как возможность применения разных методов, исходя из случая математической задачи.
Задание такого закона возможно аналитическим, графическим путем или с использованием таблицы, последние два из которых зачастую рассматривают в виде графиков и расписаний движений поездов.
Дано уравнение движения материальной точки x = 0 , 4 t 2 . Произвести запись формулы зависимости υ x ( t ) , построить график зависимости скорости от времени. На графике отметить площадь, численно равную пути, пройденному точкой за 4 секунды, произвести вычисление.
Дано: x = 0 , 4 t 2 , t = 4 c
Найти: υ x ( t ) , S — ?
Решение
При решении необходимо учитывать зависимость скорости от времени:
υ x = υ 0 x + a x t .
Зависимость координаты от времени и сравнение уравнения с заданным принимает вид:
x = x 0 + υ 0 x t + a x t 2 2 , x = 0 , 4 t 2 .
Очевидно, что x 0 = 0 , υ 0 x = 0 , a x = 0 , 8 м / с 2 .
После подстановки данных в уравнение:
Определим точки, изобразим график:
υ x = 0 , t = 0 , υ x = 4 , t = 5
Путь, по которому двигалось тело, равняется площади фигуры, ограниченной графиком, и находится с помощью формулы:
Видео:Физика 10 класс (Урок№2 - Равномерное прямолинейное движение материальной точки.)Скачать

Кинематическое уравнение движения материальной точки для координаты имеет вид х = (8 + 3t + 5t^2) м. Определите координату и скорость
Видео:Уравнение равномерного прямолинейного движения | Физика 10 класс #3 | ИнфоурокСкачать

Ваш ответ
Видео:Решение графических задач на равномерное движениеСкачать

решение вопроса
Видео:Криволинейное, равномерное движение материальной точки по окружности. 9 класс.Скачать

Похожие вопросы
- Все категории
- экономические 43,399
- гуманитарные 33,632
- юридические 17,905
- школьный раздел 607,960
- разное 16,854
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Видео:Дифференциальное уравнение движения материальной точки.Скачать

Кинематика материальной точки. Кинематическое уравнение движения материальной точки по прямой
Страницы работы
Содержание работы
Министерство образования Российской Федерации
Санкт-Петербургский государственный горный институт им. Г.В. Плеханова
Кафедра общей и технической физики
Тема: «Кинематика материальной точки»
Выполнил: студент гр. БА-02 ________________ /Михалов А.И./
Проверил: доцент ________________ /Смирнова Н.Н./
(должность) (подпись) (Ф.И.О.)
1. Формулировка задания.
Кинематическое уравнение движения материальной точки по прямой (ось x) имеет вид,
1. Путь, пройденный материальной точкой за интервал времени от t1=2.2с до t2=10с.
2. Среднюю путевую скорость V за тот же интервал времени.
3. Среднее значение ускорения.
4. Координату материальной точки в момент времени t1 и t2
Построить графики зависимостей величин V(t), а(t) при изменении времени.
2 Краткое теоретическое содержание.
Основные определения
Исходное уравнение – х=f(t)=7+3t-0,02t 3 – уравнение зависимости координаты от времени. Данное уравнение является уравнением прямолинейного движения, т.к. изменяется только одна координата.
Материальная точка – тело, размерами которого можно пренебречь по сравнению с расстоянием до других тел.
Путь (S) – расстояние по траектории (от начала движения до данной точки). [S]=м
Скорость (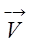
Среднепутевая скорость (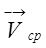
Ускорение (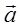
Среднее ускорение (аср) — физическая величина, которая равна отношению изменения скорости к интервалу времени.
Равнозамедленное прямолинейное движение – движение, при котором скорость материальной точки за равные промежутки времени изменяется на одну и тужу величину, причём направления вектора скорости и ускорения противоположны.)
Основные формулы, применяемые в работе.
1. Путь, пройденный материальной точкой за интервал времени от t1до t2:
Для определения пути разобьем его на два, т.к. при изменении знака проекции скорости, точка изменяет направление движения и начинает двигаться в обратном направлении:
где S1— путь, пройденный материальной точкой за время t max-t 1;
S2 — путь, пройденный материальной точкой за время t 2-t max;
t max– время в момент возврата материальной точки (когда точка начинает двигаться в обратном направлении: путь возрастает, а координата материальной точки убывает).
Чтобы найти формулы вычисления S1 и S2, схематично изобразим данное движение:
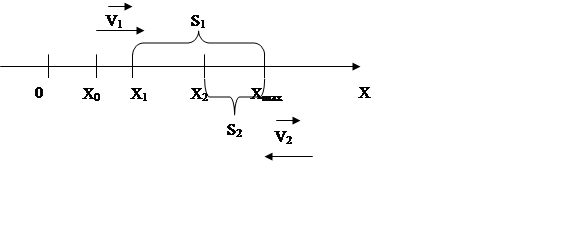 |
Из данного рисунка видно, что путь равен приращению координаты:
где x1,x2 – координаты точки в моменты времени t 1 и t 2 соответственно;
xmax – максимальная координата, которую материальная точка достигает в момент, когда начинает двигаться обратно (скорость меняет знак).
2. t max определяется приравниванием к нулю первой производной от координаты по времени, т.к. по свойству максимума в точке, в которой функция х=f(t) максимальное значение, первая производная этой функции равна нулю. Т.к. при данном движении все переменные изменяются только по координате Х, то приращение (дифиренцал) радиус-вектора равно приращению (дифиренцалу) координаты (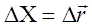
3. Средняя путевая скорость Vср за тот же интервал времени (в соответствии с определением):
4. Среднее значение ускорения (в соответствии с определением):
Т.к. скорость равна отношению приращения радиус вектора к интервалу времени, за которое это приращение произошло, то можно записать данную формулу следующим образом:
Данное кинематическое уравнение движения материальной точки 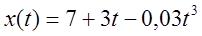
3.1. Координаты материальной точки в моменты времени t 1 и t 2 определяются подстановкой соответствующих значений моментов времени:
3.2. Для определения момента возврата найдём первую производную от координаты по времени.

3.3. Время в момент возврата материальной точки:
3.4. Максимальная координата
Подставив, значение момента возврата материальной точки в уравнение координаты определим:
3.5. Путь, пройденный материальной точкой за интервал времени от t1до t2:
3.6. Средняя путевая скорость Vср за тот же интервал:
3.7. Среднее значение ускорения:
Уравнение зависимости скорости от времени уже найден в пункте 3.2 (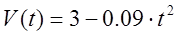
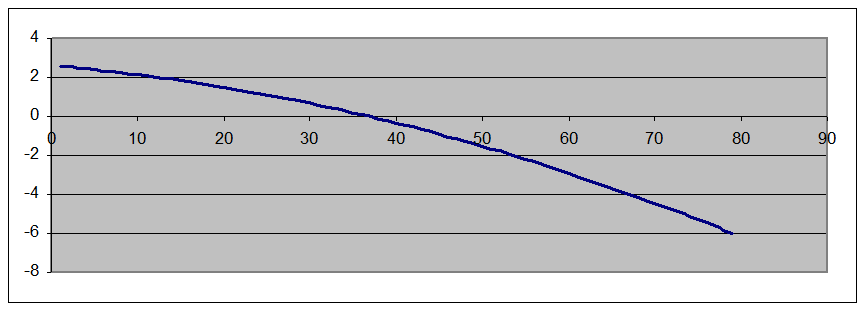
График зависимости скорости от времени.
Потому что точка меняет направление движения в момент времени t=5,77 с., график зависимости скорости от времени пересекает ось Х.
Найдём уравнение мгновенного ускорения в произвольный момент времени t. Для этого возьмём вторую производную от координаты x:
График зависимости а(t) представляет собой прямую. .
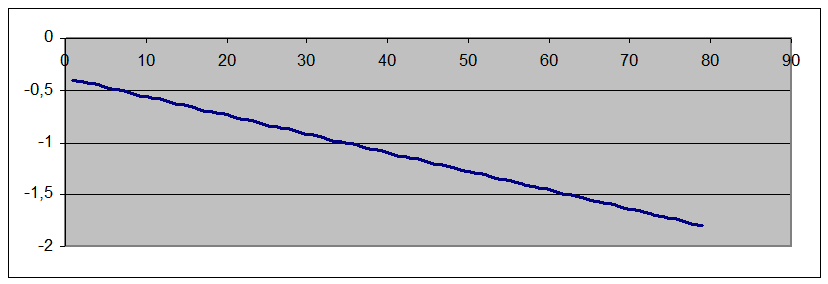 |
Вывод: В расчетно-графическом задании “Кинематика материальной точки” рассматривалось движения материальной точки по прямой. В результате решения я нашёл:
2.
3.
Построенные графики отображают зависимость а(t) и V(t).
📹 Видео
Траектория и уравнения движения точки. Задача 1Скачать

Кинематика материальной точки за 20 минут (кратко и доступно) Кинематика точкиСкачать

Урок 1. Кинематика прямолинейного движения материальной точки.Скачать

Прямолинейное равноускоренное движение. Ускорение | Физика 9 класс #5 | ИнфоурокСкачать

Исправляем автофокус и цвет на камерах FujifilmСкачать

Урок 12. Равномерное прямолинейное движениеСкачать

Равномерное прямолинейное движение - физика 9Скачать

Урок 7. Механическое движение. Основные определения кинематики.Скачать

Физика - уравнения равноускоренного движенияСкачать

Наклонное сечениеСкачать

Криволинейное, равномерное движение материальной точки по окружности. Практическая часть. 9 класс.Скачать

Физика - перемещение, скорость и ускорение. Графики движения.Скачать

Динамика материальной точки в НИСО. Нелинейное дифференциальное уравнение движенияСкачать