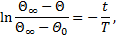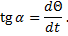Температура вынутого из печи хлеба в течение τ1 = 20 мин падает от t0 = 100 °C до t1 = 60 °C (рис. 4). Температура охлаждающего воздуха tс = 25 °C. Через какое время от момента начала охлаждения температура хлеба понизится до tк = 30 °С?
Зависимость среднеобъемной температуры тела при его охлаждении
от времени процесса
Скорость охлаждения тела представляет собой понижение температуры тела t = t(τ) в единицу времени и выражается производной. По закону Ньютона скорость охлаждения тела пропорциональна разности температур тела и окружающей среды. Это процесс неравномерный. С изменением разности температур меняется и скорость охлаждения тела.
Дифференциальное уравнение охлаждения хлеба будет 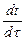
где k – коэффициент пропорциональности, tc – температура среды.
Выражение (1) точнее следует называть не законом, а уравнением, формулой Ньютона, так как коэффициент k является сложной функцией многих переменных, он зависит от следующих факторов:
– скорости среды (жидкости, газа), обтекающей тело, ее плотности и вязкости, то есть переменных, определяющих режим течения жидкости;
– тепловых свойств жидкости (удельной теплоемкости, теплопроводности, коэффициента объемного расширения);
– тепловых свойств обтекаемого тела;
– геометрических параметров – формы и определяющих размеров, а также шероховатости поверхности тела.
Из этой сложной зависимости коэффициента пропорциональности k от многих параметров процесса следует, что простота уравнения (1) только кажущаяся. При его использовании трудности, связанные с определением количества тепла, передаваемого путем конвективного теплообмена, заключается в расчете величины k. В рассматриваемой задаче считаем коэффициент k постоянной величиной,которая должна быть задана непосредственно либо дополнительным
условием, из которого коэффициент k может быть определен. Уравнение (1) – обыкновенное дифференциальное уравнение первого порядка с разделяющимися переменными. Оно аналогично дифференциальному уравнению, описывающему бесконечное замедление тела, движущегося в среде с сопротивлением, пропорциональным скорости. Пусть τ – время охлаждения. Тогда, разделяя переменные, получим:
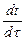

Интегрируя уравнение (2),
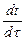
где A – произвольная положительная постоянная.
Из (4) следует общее решение уравнения (2):
Постоянную A определяем из начального условия t(0) = t0:
Коэффициент пропорциональности k определяем из данного в
задаче дополнительного условия:
при τ = τ1 t(τ1) = t1.
t1 – tс = (t0 – tс) . (7)
Таким образом, получили зависимость температуры тела от заданных начальной его температуры и температуры окружающей среды, а также от длительности процесса охлаждения. Необходимо отметить, что в данном случае можно определить только усредненную по объему температуру тела, но невозможно найти, например, температуру в центре тела либо в какой-нибудь другой его точке.
Из закона изменения температуры находим искомое время τк, необходимое для охлаждения хлеба от начальной его температуры t0 до конечной tк:
τк = τ1 мин. Замечание: если считать охлаждение тела происходящим по линейному закону (прямая АВ на рис. 4), получим искомое время охлаждения, равное 35 минутам, что, очевидно, ошибочно и недопустимо.
Контрольные вопросы:
1.Почему коэффициент пропорциональности не может быть представлен аналитической функцией?
2.Каков физический смысл начального условия для температуры и как его находить?
3.Какие методы существуют для установления адекватности результатов моделирования?
Лекция 6.Методы реализации математических моделей с применением компьютера. Понятие вычислительного эксперимента.
План лекции:
1.Какие методы существуют для реализации математических моделей на компьютере?
2. Рассмотрение аналитических методов реализации математических моделей.
3. Рассмотрение численных методов реализации математических моделей.
Цель лекции:Формирование у магистрантов понятия адекватности результатов расчетов по математическим моделям.
Знания и умения, формируемые у магистранта:умение проводить вычислительный эксперимент и устанавливать адекватность численных результатов
Форма проведения лекции:обзорная лекция
Задача 1.
Рассмотрим задачу нахождения простейшего закона нагрева теплообменника при постоянном притоке теплоты.
Решение.
Пусть Т – температура наружной поверхности теплообменника;
dT – изменение температуры отопительного аппарата в течение времени dt;
m – масса аппарата;
с – удельная теплоемкость материала аппарата;
α – коэффициент теплоотдачи (теплообмена) от поверхности аппарата;
Q – количество теплоты, поступающей в теплообменник в единицу времени;
S – поверхность теплообмена ( теплоотдачи) аппарата;
Т1 – наружная температура (температура среды);
Т – Т1 – превышение наружной температуры теплообменника над температурой среды.
Требуется найти закон Т(t).
В течение времени dt происходят следующие процессы:
а) в теплообменник поступает количество теплоты, равное Qdt;
б) количество теплоты в аппарате изменяется на величину, равную mcdТ;
в) отдается в окружающую среду количество теплоты, равное величине αS (T–T1)dt.
Суммируя эти количества, получаем уравнение теплового баланса (применение закона сохранения энергии к тепловым процессам):
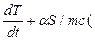
Полагая а = αS/(mc) и b = Q/(mc), получаем дифференциальное уравнение процесса (2) в следующем виде:

Разделяем переменные, преобразуя при этом левую часть уравнения (3) так, чтобы в числителе получился дифференциал знаменателя:
— 
Интегрируя (4), получаем:
где С1 = соnst> 0, откуда следует
T – T1 = 

где С = – 
Используя начальное условие Т = Т1 при t = 0, получаем
Тогда уравнение процесса примет вид:
T – T1 = 

или, подставляя значения а и b, имеем:
T = T1 + 

Рассмотрим этот закон ((7) или (6)).
При T 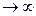


Уравнение (6) может быть записано в виде
T(t) = Тk – 
T = Tk (1 –– 
Подставляя в уравнение (9) значение t = 1/а = τ, которое называется постоянной времени, получим:
T = Tk (1 – 
Задача 2.
В культуре пивных дрожжей быстрота прироста действующего фермента пропорциональна начальной его массе. Первоначальная масса фермента а в течение часа удвоилась. Во сколько раз она увеличится через 3 часа?
Решение.
По условию задачи дифференциальное уравнение процесса

где t – время, k – коэффициент пропорциональности.
(1) – уравнение с разделяющимися переменными, его общее решение
x= C 
Из начального условия (при t = 0 =a) имеем C = а. Поэтому частное решение имеет вид
x= a 
Коэффициент k определяется из дополнительного условия:
При этих условиях из (3) следует k =
Таким образом, окончательно получаем закон, которому подчиняется данный процесс, в виде
x= a2 
где τ = 
Из (4) получаем требование задачи: при t = 3ч x= 8 а, т. е. спустя 3 часа от начала процесса масса фермента увеличится в 8 раз.
Задача 3 для самостоятельного решения.Пусть при постоянной температуре скорость растворения твердого тела в жидкости пропорциональна массе этого вещества, еще могущего раствориться до полного насыщения жидкости. Найти закон зависимости массы
растворившегося вещества от времени.
Ответ: = P (1 – 
где – масса растворившегося вещества; Р – масса вещества, дающая насыщенный раствор; t – время; k – эмпирический коэффициент пропорциональности.
Контрольные вопросы:
1. Как можно находить коэффициент пропорциональности из начальных условий?
2. Какие законы физики использованы при выводе уравнения для температуры?
3. Как можно найти ошибки моделирования, если имеются экспериментальные данные по процессу?
- Нагревание и охлаждение идеального однородного твердого тела
- Уравнение нагревания
- Установившееся превышение температуры и постоянная времени нагревания
- Решение уравнения нагревания
- Случай нагревания при Θ0 = 0
- Охлаждение тела
- Общий случай нагревания тела
- Графический способ определения T
- Заключительные замечания
- Решение задач на теплообмен с использованием уравнения теплового баланса (методические рекомендации)
- Плавление или кристаллизация
- Кипение или конденсация
- 🔥 Видео
Видео:Частное решение дифференциального уравнения. 11 класс.Скачать

Нагревание и охлаждение идеального однородного твердого тела
Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Уравнение нагревания
Хотя электрическая машина имеет сложное устройство, в основу анализа процесса ее нагревания может быть положена теория нагревания идеального однородного твердого тела, под которым здесь понимается тело, обладающее равномерным рассеянием тепла со всей поверхности и бесконечно большой теплопроводностью, вследствие чего все точки тела имеют одинаковую температуру. Составим дифференциальное уравнение нагревания такого тела, для чего рассмотрим его тепловой баланс.
Пусть в единицу времени в теле выделяется количество теплоты Q. Тогда за бесконечно малый промежуток времени выделяемое количество теплоты будет равно Q × dt. Эта теплота частично аккумулируется в теле при повышении температуры и частично отдается во внешнюю среду.
Если за время dt температура тела повысилась на dΘ, то количество аккумулируемой за это время теплоты равно G × c × dΘ, где G – масса тела и c – его удельная теплоемкость.
Пусть в рассматриваемом бесконечно малом интервале времени превышение температуры тела над температурой окружающей среды равно Θ. Тогда количество теплоты, отдаваемое в окружающее пространство за время dt вследствие лучеиспускания, конвекции и теплопроводности, будет равно S × λ × Θ × dt, где S – площадь тела и λ – коэффициент теплоотдачи с поверхности.
На основе закона сохранения энергии
| Q × dt = G × c × dΘ + S × λ × Θ × dt . | (1) |
Прежде чем приступить к решению уравнения нагревания (1), несколько преобразуем его.
Видео:Общее и частное решение дифференциального уравненияСкачать

Установившееся превышение температуры и постоянная времени нагревания
После истечения достаточно длительного времени (теоретически при t = ∞) температура тела достигает установившегося значения. Тогда dΘ = 0 и Θ = Θ∞. Подставив эти значения в выражение (1), получим
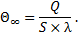 | (2) |
Установившееся превышение температуры Θ∞ тем больше, чем больше выделяется тепла и чем хуже условия ее отдачи, то есть чем меньше S × λ.
Разделим обе части выражения (1) на S × λ, используем равенство (2) и обозначим
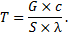 | (3) |
Тогда вместо (1) получим
| Θ∞ × dt = T × dΘ + Θ × dt. | (4) |
Размерность всех членов (4) должна быть одинакова – температура, умноженная на время. Поэтому T имеет разность времени, что можно установить также по формуле (3). Величина T называется постоянной времени нагревания тела; согласно формуле (3), она тем больше, чем больше теплоемкость тела G × c и чем меньше интенсивность отдачи тепла, то есть меньше S × λ.
Если определить из равенства (2) S × λ и подставить в (3), то получим еще одно выражение для T:
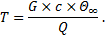 | (5) |
Числитель этого выражения равен количеству теплоты, накопленной в теле при достижении Θ = Θ∞.
Следовательно, в соответствии с выражением (5) постоянная времени нагревания T равна времени, в течение которого температура достигла бы установившегося значения Θ∞, если бы отсутствовала передача тепла в окружающую среду и все выделяемое тепло накапливалось в теле.
Видео:Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Решение уравнения нагревания
В уравнении (4) можно разделить переменные и привести его к виду
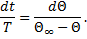 | (6) |
При интегрировании уравнения (6) получим
| t / T = – ln (Θ∞ – Θ) + C . | (7) |
Постоянная C определяется из начального условия: при t = 0 тело в общем случае имеет некоторое превышение температуры Θ = Θ0. Подставив указанные значения t и Θ в (7), найдем, что
Подставим это значение C в (7) и переменим знаки. Тогда
откуда окончательно для Θ = f(t) находим
| Θ = Θ∞ × (1 – e –t/T ) + Θ0 × e –t/T . | (8) |
Видео:2. Дифференциальные уравнения с разделяющимися переменными. Часть 1.Скачать

Случай нагревания при Θ0 = 0
В этом случае вместо выражения (8) имеем
| (9) |
чему соответствует экспоненциальная кривая нагревания, изображенная на рисунке 1, а. При малых t, когда и Θ мало, теплопередача в окружающее пространство также мала, большая часть тепла накапливается в теле и температура его растет быстро, как это видно из рисунка 1, а. Затем с ростом Θ теплоотдача увеличивается и рост температуры тела замедляется. При t = ∞, согласно равенству (9), Θ = Θ∞.
На рисунке 1, а указаны значения Θ, достигаемые через интервалы времени T, 2T, 3T и 4T. Из этого рисунка видно, что тело достигает практически установившегося превышения температуры через интервал времени t = 4T.
Видео:Видеоурок "Нахождение частных решений по виду правой части"Скачать

Охлаждение тела
Если тело имеет некоторое начальное превышение температуры Θ ≠ 0, но Q = 0 и, следовательно, в соответствии с выражением (2) Θ∞ = 0, то происходит охлаждение тела от Θ = Θ0 до Θ = Θ∞ = 0.
Подставив в (8) Θ∞ = 0, получим уравнение охлаждения тела
| (10) |
Экспоненциальная кривая охлаждения тела согласно уравнению (10) представлена на рисунке 1, б. Сначала, когда Θ и соответственно также теплоотдача велики, охлаждение идет быстро, а по мере уменьшения Θ охлаждение замедляется. При t = ∞ будет Θ = 0.
Рисунок 1. Кривые нагревания (а) и охлаждения (б) идеального однородного твердого тела
Видео:Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

Общий случай нагревания тела
| Рисунок 2. Общий случай нагревания идеального однородного твердого тела |
Общий случай нагревания тела, описываемый уравнением (8), на основании формул (9) и (10) можно рассматривать как наложение двух режимов: 1) нагревания тела от начального превышения температуры Θ = 0 до Θ = Θ∞ и 2) охлаждения тела от Θ = Θ0 до Θ = 0. На рисунке 2 кривая 3 представляет собой кривую нагревания, построенную по уравнению (8). Эту кривую можно получить путем сложения ординат кривых 1 и 2, соответствующих уравнениям (9) и (10).
Видео:Решение физических задач с помощью дифференциальных уравненийСкачать

Графический способ определения T
Найдем подкасательную бв (рисунок 1, а), отсекаемую на асимптоте Θ = Θ∞ касательной к кривой Θ = f (t). Из рисунка 1, а следует, что
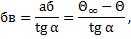 | (11) |
где α – угол наклона касательной к кривой Θ = f(t).
Но, согласно выражению (6),
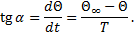 | (12) |
Подставив tg α из (12) в (11), получим
Таким образом, подкасательная к любой точке кривой нагревания или охлаждения равна постоянной времени нагревания T. Этим свойством кривых Θ = f(t) можно воспользоваться для графического определения T, если имеется кривая Θ = f(t), снятая, например, опытным путем. На рисунке 1, б и 2 показан способ определения T при построении касательной к начальной кривой.
Видео:Дифференциальные уравнения с разделяющими переменными. 11 класс.Скачать

Заключительные замечания
Выше была изложена теория нагревания идеального однородного твердого тела. В действительности электрическая машина не представляет собой такого тела, так как она состоит из разных частей, обладающих конечной теплопроводностью, причем теплопроводность электрической изоляции достаточно мала. Поэтому отдельные части машины (обмотка, сердечники и другие) имеют различные температуры. В связи с этим более правильно было бы рассматривать электрическую машину как совокупность нескольких однородных тел, между которыми существует теплообмен. В действительных условиях величина T также не вполне постоянна, так как коэффициенты теплоотдачи зависят в определенной мере от температуры. Кроме того, воздух или другой охлаждающий агент при протекании по вентиляционным каналам нагревается, и поэтому температура охлаждающей среды для различных участков охлаждаемой поверхности имеет различные значения.
Таким образом, кривые нагревания и охлаждения не являются, строго говоря, экспоненциальными. Однако в большинстве практических случаев мы не делаем существенных ошибок, считая их экспоненциальными, то есть применяя изложенную выше теорию нагревания идеального однородного тела.
Источник: Вольдек А. И., «Электрические машины. Учебник для технических учебных заведений» – 3-е издание, переработанное – Ленинград: Энергия, 1978 – 832с.
Видео:6. Особые решения ДУ первого порядкаСкачать

Решение задач на теплообмен с использованием уравнения теплового баланса (методические рекомендации)
Разделы: Физика
Пособие рекомендовано учащимся, желающим получить практические навыки в решении задач на теплообмен, и может быть полезным для учителей и абитуриентов.
При соприкосновении тел, имеющих разные температуры, между этими телами происходит теплообмен. С точки зрения молекулярно-кинетической теории, это объясняется так: молекулы более нагретого тела имеют большую кинетическую энергию, чем молекулы тела, менее нагретого. При “столкновениях” молекул соприкасающихся тел происходит процесс выравнивания их средних кинетических энергий. Молекулы более нагретого тела теряют часть своей кинетической энергии, при этом нагретое тело будет остывать. Кинетическая энергия молекул холодного тела возрастает, поэтому температура этого тела будет увеличиваться. В конечном итоге кинетические энергии молекул обоих тел сравняются, и температуры тел станут одинаковыми. На этом теплообмен прекращается.
Энергию, которую тело получает или отдаёт в процессе теплообмена, называют количеством теплоты (Q).
Количество теплоты, как и все другие виды энергии, измеряется в системе СИ в Джоулях: [Q] = Дж. (Здесь и в дальнейшем единицы измеряются в системе СИ.)
Нагревание или охлаждение
При нагревании или охлаждении тела количество теплоты, поглощаемое или выделяемое им, рассчитывается по формуле:
(t2 – t1) – разность температур тела,° С (или К);
с – удельная теплоёмкость вещества, из которого состоит тело,
Удельная теплоёмкость вещества – это количество теплоты, которое нужно сообщить одному килограмму данного вещества, чтобы увеличить его температуру на 1° С (или это количество теплоты, которое выделяет один килограмм данного вещества, остывая на 1° С).
Значения удельных теплоемкостей других веществ можно найти в справочниках, а также в школьном учебнике или задачнике.
При нагревании тела его внутренняя энергия увеличивается. Это требует притока энергии к телу от других тел. Значит, оно поглощает некоторое количество теплоты, принимая его от других тел, участвующих в теплообмене.
При охлаждении тела его внутренняя энергия уменьшается. Поэтому остывающее тело отдаёт кому-либо некоторое количество теплоты.
Обычно конечную температуру, установившуюся в результате теплообмена, обозначают греческой буквой 
В формуле (1) произведение cm для каждого конкретного тела есть величина постоянная. Её называют теплоёмкостью тела и обозначают С:
Размерность теплоемкости: 
Теплообмен между телами, имеющими одинаковые температуры, не происходит, даже если контактируют вещества, находящиеся в разных агрегатных состояниях. Например, при температуре плавления (0° С) лёд и вода могут находиться бесконечно долго, при этом количество льда и количество воды останутся неизменными. Аналогично ведут себя пар и жидкость, находящиеся при температуре кипения. Теплообмен между ними не происходит.
Плавление или кристаллизация
Если при нагревании тела его температура достигнет температуры плавления, то начинает происходить процесс перехода этого вещества из твердого состояния в жидкое. При этом идут изменения в расположении и характере взаимодействия молекул. Температура при плавлении не изменяется. Это означает, что средние кинетические энергии молекул жидкости и твердого тела при температуре плавления одинаковы. Однако внутренняя энергия тела при плавлении возрастает за счет увеличения энергии взаимодействия молекул. Количество теплоты, поглощаемое телом при плавлении, рассчитывается по формуле

где m – масса тела, кг;

При кристаллизации, наоборот, внутренняя энергия тела уменьшается на величину 
Удельная теплота плавления показывает, сколько энергии нужно сообщить одному килограмму данного вещества, взятого при температуре плавления, чтобы полностью превратить его при этой температуре в жидкость (или сколько энергии выделяет 1 кг жидкости, взятой при температуре кристаллизации, если вся она при этой температуре полностью превратится в твёрдое тело).
Удельную теплоту плавления любого вещества можно найти в справочниках. Для льда же
Температура плавления у каждого вещества своя. Её также можно найти в справочниках. Важно подчеркнуть, что температура плавления вещества равна температуре кристаллизации этого же вещества. У льда tпл = 0° С.
Кипение или конденсация
При достижении жидкостью температуры кипения начинает происходить другой фазовый переход – кипение, при котором расстояния между молекулами значительно увеличиваются, а силы взаимодействия молекул уменьшаются. Вся подводимая к жидкости теплота идет на разрыв связей между молекулами. При конденсации пара в жидкость, наоборот, расстояния между молекулами значительно сокращаются, а силы взаимодействия молекул увеличиваются. Для кипения жидкости энергию к жидкости нужно подводить, при конденсации пара энергия выделяется. Количество теплоты, поглощаемое при кипении или выделяемое при конденсации, рассчитывается по формуле:
где m – масса тела, кг; L – удельная теплота парообразования,
Удельная теплота парообразования показывает, сколько энергии нужно сообщить одному килограмму жидкости, взятой при температуре кипения, чтобы при этой температуре полностью превратить её в пар (для конденсации: сколько энергии выделяет один килограмм пара, взятого при температуре конденсации, полностью превращаясь в жидкость).
При одинаковом давлении температура кипения и температура конденсации одного и того же вещества одинаковы.
Температуры кипения и удельные теплоты парообразования также можно найти в справочниках. Для воды же они соответственно равны: рис. 9 (при нормальном атмосферном давлении).
Уравнение теплового баланса
Тела, участвующие в теплообмене, представляют собой термодинамическую систему. Термодинамическая система называется теплоизолированной, если она не получает энергию извне и не отдаёт её; теплообмен происходит только между телами, входящими в эту систему. Для любой теплоизолированной системы тел справедливо следующее утверждение: количество теплоты, отданное одними телами, равно количеству теплоты, принимаемому другими телами.
Это утверждение описывает частный случай закона сохранения и превращения энергии в применении к процессу теплообмена. А формула (5) является одним из видов уравнения теплового баланса.
При решении задач с помощью данного вида уравнения теплового баланса в формуле (1) в качестве t2 следует брать большую температуру, а в качестве t1 – меньшую. Тогда разность (t2 – t1) будет положительна и всё произведение cm(t2–t1) также будет положительным. Все теплоты, отданные и полученные, будут положительными.
Уравнение теплового баланса можно записать и в таком виде:
где n – количество тел системы.
Алгебраическая сумма всех количеств теплоты (поглощенных и выделенных) в теплоизолированной системе равна нулю.
Q1, Q2, …, Qn – это теплоты, поглощаемые или выделяемые участниками теплообмена. Очевидно, что в этом случае какие-то теплоты должны быть положительны, а какие-то – отрицательны. При записи уравнения теплового баланса в виде (6) всегда t2 – конечная температура, а t1 – начальная.
Если тело нагревается, то разность (t2 – t1) положительна и все произведение cm(t2 – t1) положительно. То есть Q > 0 тогда, когда теплота к данному телу подводится.
А если t2 0; если тело выделяет энергию (кристаллизация, конденсация), то Q
 | Проведём анализ: Вода и калориметр находились в тепловом равновесии, поэтому они имели одинаковую температуру: t1 = t2 = 20° С. При опускании в воду с температурой 20° С свинцового тела с температурой 90° С между водой и свинцом будет происходить теплообмен. Свинец будет остывать, а вода — нагреваться. В этом же процессе участвует и калориметр, который, как и вода, будет тоже нагреваться. |
 | Изменение температур тел с течением времени удобно изображать на графике зависимости t(t ). Отрезок АВ соответствует графику изменения температуры свинцового тела. Стрелка, идущая от него, показывает, что, остывая, свинец выделяет энергию Q3. |
| Два параллельных отрезка СВ соответствуют графикам изменения температур калориметра и воды. Стрелки, идущие к ним, показывают, что для нагревания калориметра и воды требуется энергия Q1 и Q2, которую они поглощают. | |
| Решим задачу с использованием уравнения теплового баланса в виде (5): |
Решим задачу с использованием уравнения теплового баланса в виде (6):
Ответ: Вода нагреется до 24° С.
Предлагаю читателю самостоятельно сделать проверку размерности.
🔥 Видео
12. Интегрирующий множитель. Уравнения в полных дифференциалахСкачать

Дифференциальные уравнения. 11 класс.Скачать

11. Уравнения в полных дифференциалахСкачать

Математика без Ху!ни. Линейное неоднородное уравнение 1 порядка. Метод вариации постоянной.Скачать

8. Дифференциальные уравнения, линейные относительно х и х'Скачать

Решение дифференциальных уравнений. Практическая часть. 11 класс.Скачать

Дифференциальные уравнения, 2 урок, Дифференциальные уравнения с разделяющимися переменнымиСкачать

13. Как решить дифференциальное уравнение первого порядка?Скачать

Найти общее решение уравнения в частных производных первого порядка.Скачать