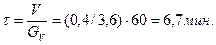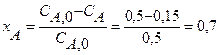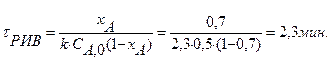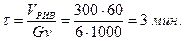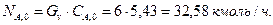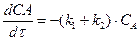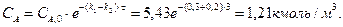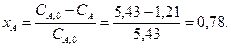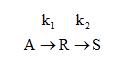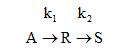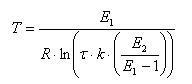Реактор идеального вытеснения характеризуется тем, что любой элемент объема реагирующей среды движется по высоте (длине) реактора параллельно другим элементам, не смешиваясь с предыдущими и последующими элементами объема.
На рис. 2 схематично показана изменение степени превращения хА, исходных концентраций СА и других параметров в реакторе идеального вытеснения. Материальный баланс такого реактора при Gнач = 0 запишется в виде:
Gпр= Gух+ Gхр (7) 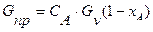 (8) (8) 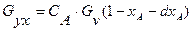 (9) (9) 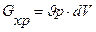 (10) (10) | 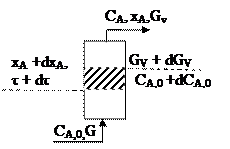 Рис.2. Схема реактора идеального вытеснения. Рис.2. Схема реактора идеального вытеснения. |
После подстановки значений составляющих материального баланса в уравнение (7) и преобразований получим:
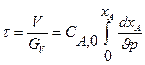
Приведенное уравнение с начальным условием V=0, СА= СА0 для некоторых видов простых химических реакций имеет аналитическое решение. В таблице 2 приведены решения уравнения (11) как расчетные формулы для реактора, работающего в режиме идеального вытеснения при проведении в нем необратимых химических реакций, когда реакционный объем остается постоянным.
Таблица 2. Расчетные уравнения для реактора идеального вытеснения
| Схема реакции | Кинетическая модель | Расчетные уравнения |
 | 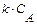 | 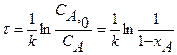 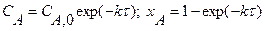 |
 | 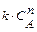 при при 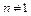 | 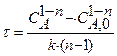 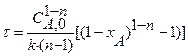 |
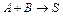 | 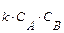  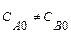 | 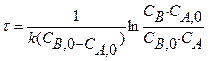 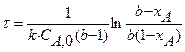 |
 |  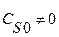 | 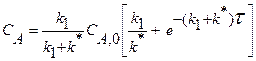 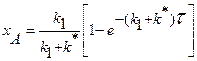 |
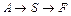 |  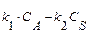 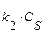 |  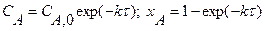 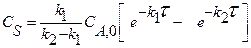  |
  |  | 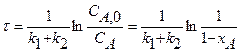 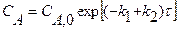  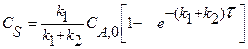 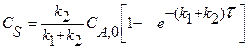 |
Пример 5.
Определить объем реактора идеального вытеснения для реакции протекающего без изменения объема реакционной массы.
порядок реакции n=1;
объемный расход исходного вещества GV = 30 л/мин;
начальная концентрация исходного вещества СА0= 0,2 моль/л;
константа скорости реакции k= 0.25 мин -1 ;
степень превращения xA = 0,82.
По базовому уравнению РИВ определяем время реакции:
Рассчитываем объем РИВ:
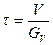
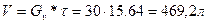
Пример 6.
Определить производительность реактора по продукту R рассчитать объем реактора идеального вытеснения для полученной производительности, если данная реакция проводиться в РИС-Н.
порядок реакции n=2;
объемный расход исходного вещества GV = 3,6 м 3 /ч;
начальная концентрация исходного вещества СА,0= 0,5 кмоль/м 3 ;
константа скорости реакции k= 2,3 л/(моль∙мин);
Определим время пребывания в реакторе смешения:
Из базового уравнения для реактора смешения находим

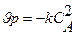
Рассчитываем степень превращения вещества А:
Находим производительность по продукту R:
Рассчитываем время пребывания в реакторе идеального вытеснения(см. таб.2):
Определяем объем реактора вытеснения по формуле:
Пример 7.
Определить мольную нагрузку на реактор по веществу А и степень превращения в реакторе вытеснения.
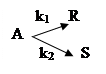
порядок реакции n=2;
объемный расход исходного вещества GV = 6 м3/ч;
концентрация продукта R на выходе из реактора равна 2.5 кмоль/м3;
константа скорости реакции k1= 0,3 мин -1 , k2= 0,2мин -1 ;
Определяем мольную нагрузку на реактор
Неизвестную начальную концентрацию вещества А на входе в реактор определяем из уравнения:
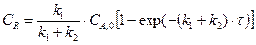
Находим время пребывания:
Рассчитываем начальную концентрацию вещества А:
Находим мольную нагрузку на реактор:
Определяем концентрацию вещества А на выходе из реактора исходя из базового уравнения для реактора вытеснения:
Интегрируя это уравнение и решая относительно СА, получаем:
Рассчитываем степень превращения вещества А:
Задачи для самостоятельного решения
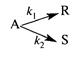
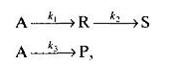
1. Жидкофазная реакция типа А→ R→S имеет константы скоростей, равные к1=2 с -1 и к2= 0,8с -1 . 4.5 ч -1 .Объемный расход исходного вещества А с концентрацией 1,8 моль/л составляет 18 м 3 /ч. Рассчитать объем реактора вытеснения для получения максимального количества вещества R, селективность и производительность по продукту R.
2. В непрерывном реакторе смешения проводится последовательная реакция типа А→R→S с константами скоростей к1=0,5 ч -1 и к2=0,8 ч -1 . Исходная концентрация вещества А равна 5 кмоль/м 3 . Продукты R и S на входе в реактор отсутствуют. Рассчитать необходимый объем реактора вытеснения, степень превращения вещества А, селективность и выход целевого продукта.
3. 

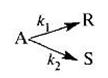
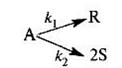
4. Процесс описывается параллельной реакцией типа
с константами скоростей к1= 0,28 мин -1 и к2 = 0,12 мин -1 . Объемный поток вещества А с концентрацией 1,6 моль/л равен 100 л/мин. Процесс проводится в реакторе вытеснения. Определить объем реактора и концентрацию вещества S при условии, что производительность по продукту R составляет 4,8 кмоль/ч.
5. 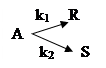
с константами скоростей к1= 0,28 л/(моль/мин)и к2 = 0,12 л/(моль/мин). Объемный поток вещества А с концентрацией 1,6 моль/л равен 100 л/мин. Объем реактора вытеснения — 0,4 м3 Определить производительность реактора продукту R и селективность процесса по веществу S.
6. Процесс описывается реакцией первого порядка типа А → 2R с константой скорости к = 0,0024 с -1 . Исходная концентрация вещества А — 1,6 моль/л. Объемный расход вещества А – 3,6 м3/ч. Заданная степень превращения по веществу А равна 0,86. Определить производительность реактора вытеснения по продукту R и его объем.
7. Процесс описывается реакцией второго порядка с константой скорости 0,023 м3/(кмоль∙ с). Исходная концентрация вещества А составляет 0,6 моль/л, объемный расход вещества А -3,6 м3/ч. Определить производительность реактора вытеснения объемом 200 л по продукту R.
8. Жидкофазная реакция типа А → 2R имеет константу скорости, равную 0,12 мин -1 . Концентрация вещества А равна 3,0 моль/л. Реакция осуществляется в реакторе вытеснения объемом 0,3 м3. Заданная степень превращения 0,88. Рассчитать производительность по продукту R.
9. Жидкофазный процесс описывается сложной реакцией.
10. Исходная смесь, в которой отсутствуют продукты реакций, подаются с объемным расходом 0,005л/с и концентрацией вещества А, равной 10 кмоль/м3. На выходе из реактора концентрации веществ равны СВ =2, СА=5, СR=1, СS=3 кмоль/м3. Определить расход реагента В.
11. Процесс описывается реакцией типа А + В→ R с константой скорости k = 0.28 л/(моль/мин). Объемные потоки вещества А с концентрацией 1,6 моль/л и вещества В с концентрацией 2,0 моль/л равны 100 л/мин. Процесс проводится в реакторе смешения объемом 1,2 м 3 . Концентрация вещества А на входе в реактор составляет 3,4 моль/л. Определить производительность реактора по продукту R.
12. Процесс описывается реакцией типа А + В → R с константой скорости k = 0,54 л/(моль/мин). Объемные потоки вещества А с концентрацией 1,8 моль/л и вещества В с концентрацией 2,7 моль/л равны 100 и 80 л/мин. Производительность реактора по продукту R составляет 8,64 кмоль/ч, концентрация продукта R на выходе — 0,8 моль/л. Определить требуемый объем реактора смешения
13. Процесс описывается реакцией типа 2А → R с константой скорости k = 0,64 л/(моль/мин). Заданная степень превращения вещества А составляет 0,8, исходная концентрация вещества А -1,8 кмоль/м 3 , производительность реактора по продукту R – 3,8 кмоль/ч. Определить требуемый объем реактора смешения.
14. Процесс описывается реакцией типа А → 2R с константой скорости k = 0,24 мин -1 . Заданная степень превращения вещества А составляет 0,8, исходная концентрация вещества А — 1,8 кмоль/м 3 , производительность реактора по продукту R – 5,8 кмоль/ч. Определить требуемый объем реактора смешения и объемный расход исходной смеси.
15. Процесс описывается обратимой реакцией первого порядка типа 2А 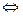
Видео:Типы Химических Реакций — Химия // Урок Химии 8 КлассСкачать

Видео:Химия | Тепловой эффект химической реакции (энтальпия)Скачать

Поиск, обзор и навигация
Магазин работ
ПиАХТ
Чертежи
Видео:Экзо- и эндотермические реакции. Тепловой эффект химических реакций. 8 класс.Скачать

Раздел 3. Химические реакторы
Задача 3.1-1 Проводится жидкофазная реакция первого порядка A -> R. Константа скорости реакции равна 0,45 мин -1 . Объемный расход реагента составляет 30 л/мин. Определить степень превращения вещества А в реакторах РИС-н и РИВ объемом 150л каждый.
Задача 3.1-2 Жидкофазная обратимая реакция 2A R проводится в РИС-н объемом 2,6 м 3 . Константа скорости прямой реакции k1=31,4 м 3 /(кмоль*мин), обратной k2=2 мин -1 . Концентрация исходного вещества 0,6 моль/л. Требуемая степень превращения хА=0,8. Определить производительность реактора по продукту R.
Задача 3.1-3 В реакторе протекает реакция второго порядка 2A = R с константой скорости реакции равной 2,8*10 -1 л/(моль*с). Начальная концентрация вещества А на входе в реактор равна 0,85 моль/л, степень превращения вещества А 0,9. Определить какое количество вещества А можно переработать в РИС-н объемом 2 м 3 и в РИВ объемом 0,6 м3.
Задача 3-1-4 Жидкофазная обратимая реакция второго порядка A + B = R + S проводится в реакторе идеального смешения объемом 40 л. Константа скорости прямой реакции k1=1,8 л/(моль•мин), обратной – k2=0,8 л/(моль•мин). Вещества А и В подаются раздельно в стехиометрическом соотношении. Концентрации веществ в индивидуальных потоках равны 0,5 моль/л. Определить, какое количество веществ А и В перерабатывается за 1 ч, если степень превращения вещества А составляет 0,85 от равновесной.
Задача 3.1-5 В жидкофазном процессе протекает реакция второго порядка 2А → R. с константой скорости реакции равной 2,3 л/(моль·мин). Объемный расход смеси с концентрацией исходного реагента СА0 = 0,5 кмоль/м 3 равен 3,6 м 3 /ч. Определить производительность РИС-н объемом 0,4 м 3 по продукту R. Рассчитать объем РИВ для полученной производительности.
Скачать решение задачи 3.1-5 (В.И. Игнатенков, В.С Бесков) (цена 200р)
Задача 3.1-6 В реакторе периодического действия при проведении реакции получены следующие результаты:
Используя данные результаты, сравнить эффективность РИВ и РИС-н для степени превращения 0,8.
Задача 3.1-7 Жидкофазный процесс, описываемый реакцией первого поряд-ка A → R, проводится в реакторе идеального смешения, время пребывания в котором составляет 360 с. Объемный расход исходного вещества равен 4 м 3 /ч. Концентрация вещества А СА0 = 2 кмоль/м 3 .
Рассчитать производительность по продукту R, если известно, что за 120 с в реакторе периодического действия в продукт превращается 40% исходного вещества.
Задача 3.1-8 Жидкофазный процесс описывается простой реакцией первого порядка A → R с константой скорости реакции k = 0,45 мин -1 . Объемный расход вещества А составляет 30 л/мин. Определить степени превращения вещества А в РИС-н и РИВ объемом по 145 л.
Задача 3.1-9 Реактор периодического действия за 8 ч работы производит 4,75 кмоль продукта. Для того чтобы загрузить реактор и нагреть его до температуры реакции, требуется 0,2 ч, а чтобы выгрузить продукт и подготовить реактор к следующему циклу, — 0,8 ч. Определить необходимый объем реактора, если 90 % поступающего в реактор исходного реагента с концентрацией 8 моль/л подвергается превращению, константа скорости реакции = 0,003 мин -1 .
Задача 3.1-10 Жидкофазный процесс описывается простой реакцией перво-го порядка с константой скорости равной 0,12 мин -1 . Концентрация вещества А в исходном потоке равна 3 кмоль/м 3 . Требуемая степень превращения вещества А ха = 0,85. Определить, какое количество вещества А можно переработать за 1 ч в реакторе идеального смешения и реакторе идеального вытеснения объемом 0,8 м 3 .
Задача 3.1-11 В реакторе периодического действия при изотермическом режиме работы и без изменения массовой плотности реакционной смеси проводят параллельную реакцию первого порядка
Через 50 мин после начала реакции 90% исходного вещества разложилось. Получившийся продукт содержит на 1 моль продукта S — 9,1 моль продукта R. На начало реакции продукты R и S отсутствовали. Определить константы скоростей реакций.
Задача 3.1-12 Жидкофазная реакция А + В → R проводится в непрерывном реакторе смешения. Константа скорости реакции k = 0,005 л/(моль•мин). Потоки веществ А и В подаются в реактор раздельно с равными объемными скоростями. Концентрации веществ в индивидуальных потоках соответственно СА = 2,4 моль/л, СВ = 3,6 моль/л. Необходимая степень превращения вещества А равна 80%. Определить допустимый расход веществ А и В в час.
Задача 3.1-13 Производство этилацетата описывается химическим уравнением:
Константа скорости прямой реакции 7,9•10 -6 м 3 /(кмоль•с), константа равновесия при температуре реакции — 2,9. Водный раствор реакционной смеси содержит 25 % массовых долей кислоты, 46 % массовых долей спирта и не содержит эфира. Требуемая степень превращения кислоты составляет 35 %.
Рассчитать объем трубчатого реактора для производства 25 т/сут этилацетата, принимая, что плотность реакционной смеси остается постоянной и равной 1020 кг/м 3 .
Скачать решение задачи 3.1-13 (В.И. Игнатенков, В.С Бесков) (цена 200р)
Задача 3.1-14 Жидкофазная реакция 2A → R + S имеет константу скорости 0,38 л/(моль•с). Объемный расход вещества А с концентрацией СА0 = 0,4 моль/л равен 40 л/мин.
Определить объемы реакторов РИС-н и РИВ при проведении процесса до степеней превращения 0,3; 0,5; 0,7; 0,9.
Задача 3.1-15 Жидкофазная необратимая реакция первого порядка проводится в реакторе смешения периодического действия без изменения массовой плотности реагирующих веществ. Продукты реакции в исходном растворе отсутствуют. За время t = 120 с в целевой продукт превращается 20% исходного вещества.
Определить степень превращения в непрерывном реакторе смешения при времени пребывания 360 мин.
Скачать решение задачи 3.1-15 (В.И. Игнатенков, В.С Бесков) (цена 200р)
Задача 3-1-16 Жидкофазная необратимая реакция первого порядка имеет константу скорости 0,45 мин -1 . Объемный расход реагента А с концентрацией СА0 = 1,6 моль/л составляет 3,6 м 3 /ч.
Определить производительность по продукту R в реакторе идеального смешения и реакторе идеального вытеснения, если их объемы равны 145 л.
Задача 3.1-17 Жидкофазная реакция A → 2R имеет константу скорости реакции равную 3,8ч -1 . Объёмный расход исходного вещества составляет 33,5 м 3 /ч. Концентрация СА0=0,8 моль/л. Рассчитать суточную производительность по продукту R для реактора смешения объемом 4м.
Задача 3.1-18 Жидкофазная обратимая реакция второго порядка 2А ↔ R + S имеет константу скорости прямой реакции k = 2-10 -3 м 3 /(кмоль*с) и константу равновесия КP = 9. Объемный расход исходного вещества с концентрацией СA0 = 1,5 моль/л составляет 4,8 м3/ч, требуемая степень превращения вещества А — 80% равновесной степени превращения.
Определить необходимые объемы реакторов идеального смешения и идеального вытеснения для проведения данного процесса.
Задача 3.1-19 Жидкофазная реакция A + B = R + S с константой скорости прямой реакции k1 = 1,8 л/(моль•мин) и константой скорости обратной реакции k-1 = 0,8 л/(моль•мин), проводится в реакторе идеального смешения объемом 40 л. Потоки веществ А и В подаются в реактор раздельно с равными концентрациями СА = СВ = 0,8 моль/л. Вещества А и В в реакторе находятся в стехиометрическом соотношении. Требуемая степень превращения вещества А хА = 0,9 хАравн. Рассчитать объемный расход реагентов.
Задача 3.1-20 Жидкофазная реакция 2А → R с константой скорости реакции равной 0,4 мин -1 проводится в реакторе идеального смешения объемом 0,5 м 3 . Объемный расход вещества А составляет 20 л/мин. Определить какую степень превращения можно достигнуть в этих условиях, и рассчитать объем реактора идеального вытеснения для достижения той же степени превращения и производительность по продукту R.
Задача 3.1-21 В непрерывном реакторе идеального смешения осуществляется жидкофазный процесс, описываемый последовательной реакцией
Константы скорости реакций k1=0,6 ч -1 , k2=0,8 ч -1 . Объёмный расход реакционной смеси равен 2,4 м 3 /ч. Исходные концентрации веществ соответственно: СА0=5моль/л, СR0=СS0=0.
Рассчитать необходимый объем реактора для получения максимального выхода целевого продукта R, степень превращения исходного вещества А, селективность и выход по целевому продукту, суточную производительность по продукту R.
Задача 3.1-22 В непрерывном реакторе идеального вытеснения осуществляется жидкофазный процесс, описываемый последовательной реакцией
Константы скорости реакций k1=0,6 ч -1 , k2=0,8 ч -1 . Объёмный расход реакционной смеси равен 2,4 м 3 /ч. Исходные концентрации веществ соответственно: СА0=5моль/л, СR0=СS0=0.
Рассчитать необходимый объем реактора для получения максимального выхода целевого продукта R, степень превращения исходного вещества А, селективность и выход по целевому продукту, суточную производительность по продукту R.
Задача 3.1-23 В проточном реакторе идеального смешения проводится реакция:
A+B -k→R
Однако вещества А и В склонны к полимеризации, описываемой уравнениями:
2A -k2 → S и 2B -k2 → D
Определить оптимальное соотношение А и В в реакторе для получения максимального выхода целевого продукта R.
Задача 3.1-24 Жидкофазный процесс описывается сложной параллельной реакцией
Объемный расход вещества А с концентрацией СА0 = 0,8 кмоль/м 3 равен 2,4 л/мин. Требуемая степень превращения xА = 0,85.
Выбрать тип реактора, рассчитать его объем, интегральную селективность и производительность по целевому продукту R, если: 1) k1 = 1,5 мин -1 ; k 2 = 4 мин -1 ; 2) k 1 = 4 мин -1 ; k 2 = 1,5 мин -1 .
Скачать решение задачи 3.1-24 (В.И. Игнатенков, В.С Бесков) (цена 200р)
Задача 3.1-25 Жидкофазный процесс описывается последовательной реакцией
Константы скорости реакций k1=2 ч -1 , k2=0,8 ч -1 . Объёмный расход реакционной смеси равен 1,2 м 3 /ч. Исходная концентрация вещества А равна СА0=1,8моль/л.
Рассчитать объем реактора идеального смешения для получения С, селективность и производительность по продукту R.
Задача 3.1-26 Жидкофазный процесс описывается реакцией:
A -k1 → R
A -k 2 → S
Константы скоростей реакции k 1 = 3,8 мин -1 ; k 2 = 1,5 мин -1 . Исходная концентрация вещества А с равна 1,4 моль/л. Требуемая степень превращения хА = 0,9.
Определить какое количество вещества А можно переработать в РИС-н объемом 0,6 м 3 и в РИВ объемом 0,2 м 3 . Рассчитать селективность и производительность по целевому продукту R.
Задача 3.1-27. Газофазная необратимая реакция второго порядка А → 3R исследовалась в опытном реакторе, представляющем собой трубу длиной 1,8 м и диаметром 2,54 см. Реакцию изучали при температуре 350 °С под давлением 4,9*10 5 Па. Расход исходной смеси газа составлял 31*10 -5 м 3 /с. При этих условиях была достигнута степень превращения ХА = 0,6. Промышленный процесс проводят при температуре 350 °С и давлении 2,45*10 6 Па. Мощность промышленной установки по газу составляет 2,35*10 -2 м 3 /с. Исходная газовая смесь содержит 50% вещества А и 50% инерта. Требуемая степень превращения 0,8.
Определить, какое количество труб указанного размера должен иметь промышленный реактор.
Задача 3.1-28 Газофазный процесс, описываемый простой необратимой ре-акцией 2A → 3R + S первого порядка, проводится при температуре 457 °С и давлении 9,8*10 5 Па. Константа скорости равна 1,25*10 -3 с -1 , скорость подачи исходного реагента — 2,5*10 -3 кмоль/с, требуемая степень превращения 0,9.
Определить объем реактора идеального вытеснения для проведения данного процесса.
Задача 3.1-29 Газофазная реакция А → S осуществляется в реакторе идеального вытеснения до степени превращения равной 0,9. Константа скорости реакции k = 2,3•10 -2 с -1 . В реактор подается исходный реагент А в количестве 2•10 -4 кмоль/с при температуре 227 °С и давлении 9,8•10 4 Па.
Рассчитать требуемый объем реактора.
Задача 3.1-30 Определить объем реактора идеального вытеснения для проведения процесса разложения фосфина. Реакция 2РН3 = 2Р(г) + 3Н2 протекает по первому порядку.
Процесс проводится под давлением 4,51*10 5 Па и при температуре 377 °С. Расход фосфина составляет 5,03*10 -4 кмоль/с. Константа скорости реакции равна 2,78*10 -3 с -1 .
Газовая постоянная К = 0,804*10 4 Па-м 3 /(кмоль*град). Требуемая степень превращения фосфина равна 0,8.
Задача 3.1-31 Реакция метана с серой СН4 + 2S2 = CS2 + 2H2S проводится при температуре 873 К и атмосферном давлении в реакторе идеального вытеснения. Расход серы в общем количестве газа, подаваемого в реактор, в 2 раза больше, чем расход метана. Константа скорости реакции k= 11,9 м 3 /(моль•ч).
Определить время пребывания реакционной смеси в реакторе для достижения степени превращения метана равной 0,7.
Задача 3.1-33 Жидкофазный процесс, описываемый обратимой реакцией второго порядка A + B = R + S с константами скорости прямой k1 = 22 л/(моль-мин) и обратной k-1 = 2 л/(моль-мин) реакций, проводится в РИС-н объемом 0,5 м 3 . Потоки веществ А и В подаются в реактор раздельно с равными концентрациями САисх=СВисх. После взаимного разбавления потоков концентрация СА0 = 1,6 кмоль/м3, а соотношение концентраций СА0:СВ0 = 1:1,5. Процесс проводится до хВ = 0,6.
Определить объемные потоки исходных веществ и производительность по продукту R. Рассчитать производительность системы состоящей из трех реакторов указанного объема, соединенных последовательно, при достижении заданной степени превращения.
Задача 3.1-34 Жидкофазный процесс описывается сложной реакцией
A + 3B = D + S
2А= R
2R = Р
Исходная смесь, в которой отсутствуют продукты реакций, подается с объемным расходом 5 л/с и концентрацией вещества А СА0 = 10 кмоль/м 3 . На выходе из реактора концентрации CB = 2, СA = 5, CR = 1, CS = 3кмоль/м 3 Определить расход реагента В.
Задача 3.1-35. Процесс описывается реакцией второго порядка типа 2А → R с константой скорости равной 2,8*10 -2 м 3 /(кмоль с). Исходная концентрация вещества А в потоке составляет 0,8 кмоль/м 3 . Требуемая степень превращения вещества А состовляет 0,85. Определить часовую производительность по продукту R в реакторе вытеснения объемом 0,6 м 3 и в реакторе смешения объемом 2 м 3 .
Задача 3.1-36. Жидкофазный процесс описывается последовательной реакцией типа
Константы скорости реакций k1=0,5 ч -1 , k 2 =0,8 ч -1 . Исходная концентрация вещества А равна 1,8моль/л. Объёмный расход вещества а составляет 18 м 3 /ч. Рассчитать объем реактора смешения для получения максимального количества вещества R, селективность и производительность по продукту R.
Задача 3.1-37 Жидкофазная реакция типа А=2R имеет константу скорости k=0,12мин -1 . Концентрация вещества А равна 3,0моль/л. Реакция осуществляется в реакторе вытеснения объемом 0,3. Заданная степень превращения вещества А составляет 0,88. Определить производительность по продукту R.
Задача 3.1-38 Жидкофазная реакция типа А=2R имеет константу скорости k=3,8 ч -1 Объемный расход исходного вещества с концентрацией 0,8 моль/л составляет 14,5 м 3 /ч.
Определить суточную производительность по продукту R для реактора смешения объемом 4 м 3 .
Задача 3-1-40 Жидкофазный процесс описывается реакцией первого порядка с константой скорости 0,12 мин -1 . Концентрация вещества А в исходном потоке равна 3 кмоль/м3. Требуемая степень превращения вещества А составляет 0,88.
Определить какое количество вещества А можно переработать в реакторе идеального смешения объемом 3,6 м3.
Задача 3.1-41 Процесс описывается реакцией второго порядка с константой скорости реакции равной 2,3*10 -3 м 3 /(кмоль*с). Исходная концентрация вещества А составляет 0,6 моль/л, объемный расход вещества А — 3,6 м3/ч. Определить производительность реактора смешения объемом 0,4 м 3 по продукту R.
Задача 3.1-42. Процесс описывается реакцией второго порядка с константой скорости 2,3-10 -2 м 3 /(кмоль-с). Исходная концентрация вещества А составляет 0,6 моль/л, объемный расход вещества А — 3,6 м 3 /ч.
Определить производительность реактора вытеснения объемом 200 л по продукту R.
Задача 3.1-43 Процесс описывается реакцией первого порядка А -> 2R с константой скорости 2,3*10 -3 с -1 . Исходная концентрация вещества А составляет 1,6 моль/л, объемный расход вещества А = 3,6 м 3 /ч. Заданная степень превращения по веществу А равна 0,86.
Определить производительность реактора вытеснения по продукту R и его объем.
Задача 3.1-44 Процесс описывается реакцией первого порядка типа А=2R с константой скорости k=2,3*10 -3 с -1 . Исходная концентрация вещества А составляет 1,6 моль/л, заданная степень превращения по веществу А – 0,86. Объём реактора смешения равен 0,3 м 3 .
Определить, какое количество вещества А можно переработать за сутки.
Задача 3.1-45 Процесс описывается обратимой реакцией первого порядка А 2R с константами скоростей k1 = 2,4 ч -1 (прямой реакции), k2 = 0,4 л/(моль*ч) (обратной). Исходная концентрация вещества А составляет 1,6 моль/л. Заданная степень превращения вещества R равна 0,9 равновесной. Объем реактора смешения составляет 0,3 м 3 . Определить производительность реактора по веществу R за сутки.
Задача 3.1-46 Процесс описывается обратимой реакцией первого порядка 2А R с константами скоростей k1 = 61,4 м /(моль*ч) (прямой реакции), k2 = 2,4 ч (обратной). Исходная концентрация вещества А составляет 1,4 моль/л. Заданная степень превращения вещества R равна 0,8 равновесной. Объем реактора смешения составляет 0,22 м3. Определить производительность реактора по веществу R за час.
Задача 3.1-47 Процесс описывается реакцией первого порядка типа А=2R с константой скорости k=0,6 мин -1 . Заданная степень превращения по веществу А – 0,85. Исходная концентрация вещества А составляет 1,8 кмоль/м3, производительность реактора по продукту R= 5,8кмоль/ч. Определить требуемый объем реактора вытеснения.
Задача 3.1-48 Процесс описывается реакцией первого порядка типа А=2R с константой скорости k=0,24 мин -1 . Заданная степень превращения по веществу А = 0,8. Исходная концентрация вещества А составляет 1,8 кмоль/м , производительность реактора по продукту R= 5,8кмоль/ч.
Определить требуемый объем реактора смешения и объемный расход исходной смеси.
Задача 3.1-49. Процесс описывается реакцией типа 2А → R с константой скорости равной 0,64 л/(моль мин). Заданная степень превращения вещества А состовляет 0,8, исходная концентрация вещества А составляет 1,8 кмоль/м 3 , производительность реактора по продукту R = 3,8 кмоль/ч. Определить требуемый объем реактора смешения.
Задача 3.1-50. Процесс описывается реакцией типа 2А → R с константой скорости равной 0,24 л/(моль*мин). Исходная концентрация вещества А составляет 1.8 кмоль/м 3 , производительность реактора по продукту R = 3,8 кмоль/ч, концентрация продукта R на выходе – 0,8 моль/л.
Определить требуемый объем реактора вытеснения и получаемую степень превращения вещества А.
Задача 3.1—51. Процесс описывается реакцией типа 2А → R с константой скорости равной 0,24 л/(моль мин). Исходная концентрация вещества А составляет 1.8 кмоль/м 3 . Процесс проводится в реакторе вытеснения объемом 0,8 м 3 . Объемный расход вещества А равен 1,8 м 3 /ч. Определить производительность реактора по продукту R.
Задача 3.1-52 Процесс описывается реакцией типа А + В = R с константой скорости равной 0,54 л/(моль/мин). Объемные потоки вещества А с концентрацией 1,8 моль/л и вещества В с концентрацией 2,7 моль/л равны 100 и 80 л/мин. Производительность реактора по продукту R составляет 8,64 кмоль/ч, концентрация продукта R на выходе — 0,8 моль/л. Определить требуемый объем реактора смешения.
Задача 3.1-53 Процесс описывается реакцией типа А + В → R с константой скорости равной 0,28 л/(моль/мин). Объемные потоки вещества А с концентрацией 1,6 моль/л и вещества В с концентрацией 2,0 моль/л равны 100 л/мин. Процесс проводится в реакторе смешения объемом 1,2 м 3 . Определить производительность реактора по продукту R.
Задача 3.1-54. Процесс описывается параллельной реакцией типа
с константами скоростей k1=2,8*10 -1 л/(моль*мин) и k2=0,12 л/(моль*мин). Объемный поток вещества А с концентрацией 1,6 моль/л равен 100 л/мин, объем реактора смешения -1,2м 3 .
Определить производительность реактора и селективность процесса по веществу R
Задача 3.1-55. Процесс описывается параллельной реакцией типа
с константами скоростей k1=2,8*10 -1 л/(моль*мин) и k2=0,12 л/(моль*мин). Объемный поток вещества А с концентрацией 1,6 моль/л равен 100 л/мин, объем реактора вытеснения -0,4 м 3 .
Определить производительность реактора и селективность процесса по веществу S.
Задача 3.1-56. Процесс описывается параллельной реакцией типа
с константами скоростей k1=2,8*10 -1 л/(моль*мин) и k2=0,12 л/(моль*мин). Объемный поток вещества А с концентрацией 1,6 моль/л равен 100 л/мин. Процесс проводится в реакторе вытеснения. Определить объем реактора и концентрацию вещества S при условии, что производительность реактора по продукту R составляет 4,8 м 3 .
Задача 3.1-57. Процесс описывается параллельной реакцией типа
с константами скоростей k1=2,8*10 -1 л/(моль*мин) и k2=0,12 л/(моль*мин). Объемный поток вещества А с концентрацией 1,6 моль/л равен 100 л/мин. Процесс проводится в реакторе смешения. Определить объем реактора и достигаемую в нем степень превращения вещества А при условии, что производительность по продукту R составляет 4,8кмоль/ч.
Задача 3-1-58. Процесс описывается параллельной реакцией типа с константами скоростей k1 = 2,8*10 -1 л/(моль*мин) и k2 = 0,12 л/(моль*мин). Поток вещества А поступает с концентрацией 1,6 моль/л. Процесс проводится в реакторе вытеснения объемом 140л. Степень превращения вещества А составляет 0,7.
Определить производительность реактора по продукту R.
Задача 3.1-59 Процесс описывается параллельной реакцией типа:
A -(k1) → R
A -(k2) → S
с константами скоростей k1 = 2,8*10 -1 л/(моль*мин) и k2 = 0,12 л/(моль*мин). Поток вещества А поступает с концентрацией 1,6 моль/л. Процесс проводится в реакторе смешения объемом 200 л. Степень превращения вещества А составляет 0,8. Определить допустимый расход вещества А.
Задача 3.1-60 Процесс описывается параллельной реакцией типа:
A -(k1) → R
A -(k2) → S
с константами скоростей k1 = 1,8*10 -1 л/(моль*мин) и k2 = 0,06*10 -1 л/(моль•мин). Объемный поток вещества А равен 250 л/мин. Процесс проводится в реакторе смешения объемом 250 л. Концентрация вещества R на выходе из реактора равна 1,2 моль/л.
Определить концентрацию вещества А на входе в реактор и степень превращения вещества А.
Задача 3.1-61 Процесс описываемый последовательной реакцией типа A → R → S с константами скоростей k1 = 1,8•10 -1 л/(моль•мин) и k2 = 0,06 л/(моль•мин). Объемный поток вещества А равен 40л/мин. Процесс проводится в реакторе смешения объемом 60 л. Концентрация вещества А на входе в реактор составляет 2,4 моль/л. Определить концентрации веществ на выходе из реактора.
Задача 3.1-62 Процесс описываемый последовательной реакцией типа A → R → S с константами скоростей k1 = 1,8*10 -1 л/(моль*мин) и k2 = 0,06 л/(моль*мин). Объемный поток вещества А равен 40л/мин. Процесс проводится в реакторе смешения объемом 260 л. Концентрация вещества А на входе в реактор составляет 2,4 моль/л. Определить производительность реактора по продукту R, степень превращения вещества А и селективность по продукту R.
Задача 3.1-63 Процесс описываемый последовательной реакцией типа A → R → S с константами скоростей k1=2,4*10 -1 л/(моль*мин) и k2=0,18 л/(моль*мин). Объемный поток вещества А равен 3,6 м 3 /ч. Процесс проводится в реакторе смешения объемом 240 л. Концентрация вещества А на входе в реактор составляет 3,4 моль/л.
Определить концентрации всех веществ на выходе из реактора, степень превращения А и селективность по продукту R.
Задача 3.1-65 Процесс описываемый последовательной реакцией типа A → R → S с константами скоростей k1 = 1,2*10 -1 л/(моль*мин) и k2 = 0,8 л/(моль*мин). Объемный поток вещества А равен 3,6 м 3 /ч. Концентрация вещества А на входе в реактор составляет 3,4 моль/л, а степень првращения его — 0,48. Определить концентрации веществ R и S на выходе из реактора и объем реактора смешения.
Задача 3.1-66. В непрерывном реакторе идеального смешения проводится последовательная реакция типа
Константы скорости реакций k1=2 ч -1 , k2=0,8 ч -1 . Исходная концентрация вещества А равна СА0=5 кмоль/м 3 . Продукты R и S на входе в реактор отстутствуют. Рассчитать необходимый объем реактора смешения для максимального выхода целевого продукта R, степень превращения исходного реагента, селективность и выход по целевому продукту, если объёмный расход составляет 2,4 м 3 /ч.
Задача 3.1-67 По условию задачи 3.1-66 рассчитать необходимый объем реактора вытеснения, степень превращения вещества А, селективность и выход целевого продукта.
3.1-66 (условие) В непрерывном реакторе смешения проводится последовательная реакция типа А → R → S с константами скоростей k1 = 0,5 ч -1 и k 1 = 0,8 ч -1 . Исходная концентрация вещества А равна 5 кмоль/м 3 . Продукты R и S на входе в реактор отсутствуют. Рассчитать необходимый объем реактора смешения для максимального выхода целевого продукта R, степень превращения исходного реагента, селективность и выход по целевому продукту, если объемный расход составляет 2,4 м 3 /ч.
Скачать решение задачи 3.1-67 (В.И. Игнатенков, В.С Бесков) (цена 200р)
Задача 3.1-70 Жидкофазная реакция типа A → 2R имеет константу скорости равную 3,8 ч -1 . Объемный расход исходного вещества с концентрацией 0,8 моль/л составляет 14,5 м 3 /ч.
Рассчитать суточную производительность по продукту R для реактора смешения объемом 4 м3.
Задача 3.2-1 В проточном реакторе идеального смешения проводится обратимая экзотермическая реакция первого порядка.
Показать, что температура, при которой будет достигнута максимальная степень превращения, определяется формулой
Считать, что константы скорости реакции, энергии активации и время пребывания смеси в реакторе заданы.
Скачать решение задачи 3.2-1 (В.И. Игнатенков, В.С Бесков) (цена 200р)
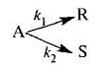
Задача 3.2-2 Процесс, описываемый параллельной реакцией
протекает в диапазоне температур от 573 до 773 К.
При какой температуре необходимо проводить процесс, чтобы обеспечить образование максимального числа молей продукта R в реакторах идеального вытеснения и идеального смешения непрерывного действия, если константы скорости, с -1 , описываются уравнениями k1= 10 15 exp[–20000/(RT)], k2 = 10 14 ехр[–10000/(RT)]?
Задача 3.2-3 Процесс, описываемый параллельной реакцией
Проводиться в реакторе идеального смешения при изотерическом режиме работы.
Определить температуру, при которой должен работать реактор, чтобы на образование 2 моль продукта R образовывался 1 моль продукта S.
Константы скоростей реакции, с -1 , определяются уравнениями: k1=6*10 13 ехр [-37000/(RT)] , k2= 3,7*10 13 ехр [-40000/(RT)] .
Задача 3.2-5 Жидкофазный процесс, описываемый параллельно-последовательной реакцией
осуществляется в проточном реакторе идеального смешения. Константы скорости, с-1, реакции: k1= 10 10 ехр [-64000/(RT)] ; k2 =10 8 ехр [-80000/(RT)] ; k3 = 10 7 exp [-40000/(RT)] .
Определить оптимальную температуру, при которой будет, достигнут максимальный выход продукта R, если требуемая степень превращения исходного вещества составляет 80%.
Задача 3.2-6 В каскаде из трех реакторов равного объема проводится жидко-фазная реакция А = R + Qp при температуре 368 К. Тепловой эффект реакции равен 1,67*10 6 Дж/кг. Константа скорости реакции, с -1 , описывается уравнением k = 4•10 6 ехр (–7900/Т) . Произведение pср= 4,2*10 6 Дж/град правильная размерность (кг/м3•Дж/(кг*град) = Дж/(м3*град)) остается постоянным и не зависит от степени превращения и температуры. Исходная концентрация вещества А в потоке равна 1 кмоль/м 3 , молярная масса вещества А – 100 кг/кмоль, производительность каскада по продукту R — 0,375*10 -3 кмоль/с, требуемая степень превращения вещества А – 0,95. Первый реактор каскада работает в адиабатическом режиме, второй и третий — с отводом теплоты. Температура реакционной смеси падает в трубопроводах между первым и вторым реактором на 3 град, а между вторым и третьим па 5 град. Коэффициент теплопередачи во втором и третьем реакторе от реакционной смеси к охлаждающей воде равен 11000 Вт/(м 2 *К). Температура охлаждающей воды в теплообменниках второго и третьего реакторов составляет 288 К.
Определить: поверхность теплообмена во втором и третьем реакторах каскада; необходимую температуру смеси на входе в первый реактор каскада; объем единичного реактора каскада. Показать, что первый реактор каскада работает в устойчивом режиме.
Задача 3.2-7 Газовая смесь поступает в реактор со скоростью 2,5*10 -3 кмоль/с. Начальная температура смеси – 833 К, давление — 5*10 5 Па, диаметр реактора – 0,2 м. В реакторе адиабатически протекает химическая реакция А + В = R + Qp. Состав исходной смеси в молярных долях, %, следующий: 40 – А, 40 – В и 20 – инертных газов. Теплоемкости исходных реагентов, продуктов реакции и инертных газов соответственно равны 25*10^3, 42*10 3 , 21*10 3 Дж/(кмоль*К). Тепловой эффект реакции при температуре 278 К составляет 53,3*10 6 Дж/кмоль. Зависимость константы скорости от температуры:
Определить необходимую длину реактора для достижения степени превращения по веществу А равной 95 %.
Задача 3.2-8 В проточном реакторе идеального смешения объемом 2 м 3 проводится необратимая экзотермическая реакция с константой скорости, с-1, описываемой уравнением k = 10 12 ехр [-90000/(/R*T)] . Теплоемкость реакционной смеси равна 20790 Дж/(кг*К) и не зависит от температуры и степени превращения. Плотность реакционной смеси остается постоянной и равной 1000 кг/м3.
Исходный реагент с концентрацией 6 кмоль/м 3 подается в реактор со скоростью 5 м 3 /ч. Тепловой эффект реакции равен 96600 Дж/моль. Температура в реакторе не должна превышать 333 К.
Рассчитать, при какой температуре следует подавать исходный раствор, чтобы процесс протекал в адиабатическом режиме.
Задача 3.2-9 В реакторе идеального вытеснения, работающем в адиабатическом режиме, протекает необратимая экзотермическая реакция первого порядка.
Определить минимальную температуру, которую необходимо под-держивать на входе в реактор, чтобы обеспечить устойчивый режим работы, если тепловой эффект реакции равен 13500 Дж/моль, а удельная теплоемкость реакционной смеси ср = 145 Дж/(моль-К). Связь степени превращения и температуры представлена следующими данными:
х 0,1 0,25 0,58 0,72 0,88 0,9
Т, К 283 293 303 313 323 333
Задача 3.2-10 В реакторе идеального смешения объемом 0,3 м 3 проводится экзотермическая реакция первого порядка А > R + Qp. Константа скорости реакции, мин -1 , описывается уравнением k = 10 3 ехр[-20000/(RT)]. Тепловой эффект реакции сосавляет 9637 кДж/кмоль. Плотность реакционной массы не зависит от температуры и степени превращения и равна 420 кг/м 3 , удельная теплоемкость раствора — 3,8 кДж/(кг•К). Растворе реагента А подается в реактор с концентрацией 6 кмоль/м 3 в количестве 0,6 м 3 /ч.
Рассчитать, при какой температуре следует подавать исходный раствор компонента А в реактор, работающий в адиабатическом режиме, чтобы температура в нем не превышала 60 °С.
Скачать решение задачи 3.2-10 (В.И. Игнатенков, В.С Бесков) (цена 200р)
Задача 3.2-11 Определить максимальную производительность установки, состоящей из двух реакторов, соединенных последовательно: реактора идеального смешения объемом 0,6 м 3 и реактора идеального вытеснения объемом 0,1 м 3 , при проведении реакции 2A -> R + Qр. Константа скорости реакции, м3/(кмоль-с), описывается уравнением k = 4*10 9 ехр(-8000/T). Концентрация реагента А в исходном потоке равна 0,5 кмоль/м3. Исходная температура потока составляет 20 °С, адиабатический разогрев — 60 °С, требуемая степень превращения — 0,96. Установка работает в адиабатическом режиме.
Задача 3.2-12 В реакторе идеального вытеснения проводится реакция А +В = R + S +Qp в адиабатическом режиме. Концентрации веществ А и В в исходных потоках равны 2,4 кмоль/м3. Общий расход реакционной смеси составляет 1,55•10 -3 м 3 /с, начальная температура потока — 20 °С, температура реакционной смеси на выходе из реактора — 53 °С, Константа скорости реакции описывается уравнением
k = 6,52*10 5 exp(-5,1*10 3 /Т)
Определить объем реактора, необходимый для достижения степени превращения по веществу А равной 0,82
Задача 3.2-13 Определить температуру проведения реакции и степень пре-вращения, которые будут достигнуты, если реакцию A → R + Qp про-водить в адиабатическом режиме в реакторе идеального смешения объемом 0,05 м 3 . Объемный расход реагента А с концентрацией 3 кмоль/м 3 равен 1,75*10 3 м 3 /с, константа скорости реакции, с-1, описывается уравнением k = 10 5 ехр[-45300/(R*T)]. Тепловой эффект реакции составляет 2,8*10 7 Дж/кмоль. Плотность реакционной смеси равна 524 кг/м3, а теплоемкость — 1200 Дж/(кг-К) и не зависят от степени превращения. Температура входящего потока — 325 К.
Задача 3.2-14 В реакторе идеального вытеснения объемом 1,26 м3, работающем в адиабатических условиях, проводится реакция первого порядка 2А = R + Qp, с константой скорости, с -1 , описываемой уравнением k = 10 13 ехр[-1200/T]. В реактор подается поток с концентрацией вещества А 3,2 кмоль/м3 при 325 К. Температура реакционной смеси на выходе из реактора составляет 357 К, тепловой эффект реакции — 2,7*10 7 Дж/кмоль, теплоемкость реакционной смеси — 2,2*10 3 Дж/(кг*К), плотность реакционной смеси — 850 кг/м3. Определить производительность реактора по продукту R.
Задача 3.2-15 Необратимую экзотермическую реакцию А = R + Qp с тепловым эффектом равным 2*10 7 Дж/кмоль проводят в адиабатическом реакторе идеального смешения объемом 10 м 3 . Константа скорости, с -1 , описывается уравнением k = 10 13 ехр(-12000/Т). Плотность раствора не зависит от степени превращения и температуры и равна 850 кг/м 3 . Удельная теплоемкость постоянна и равна 2200 Дж/(кг*К). Раствор с концентрацией реагента А равной 5 кмоль/м 3 подается в реактор в количестве 10 -2 м 3 /с.
Определить температуру проведения реакции и степень превращения, если раствор реагента А продается при: 290; 300; 310 К.
Задача 3.2-16 В реакторе идеального смешения непрерывного действия, работающем в адиабатическом режиме, проводится реакция A + B -> R + S + Qp константой скорости, л/(моль-с), описываемой уравнением k = 5,08*10 5 ехр[-4,23*10 4 /(R*T)], и тепловым эффектом равным 75000 кДж/(моль-А). Концентрации исходных реагентов САО = Сво = 1,2 кмоль/м3. Темлоемкость реакционной смеси постоянна и равна 1,8 кДж/(кг-К). Исходный раствор подается с температурой 20 °С в количестве 12 м 3 /ч. Определить объем реактора для достижения степени превращения
Задача 3.2-18 В реакторе идеального смешения непрерывного действия проводится экзотермическая реакция А -> R + Qр с тепловым эффектом равным 190 кДж/кмоль. Расход реагента А с температурой 15 °С составляет 0,2 кмоль/с, теплоемкость реакционной смеси — 16,7 кДж/(кмоль*К), температура реакционной смеси на выходе из реактора — 49 °С, степень превращения по веществу А — 0,8, средняя разность температур между охлаждающим агентом и реакционной смесью — 10 град, коэффициент теплопередачи равен 419 кДж/(м2*с*К).
Определить количество отводимой или подводимой теплоты и требуемую площадь теплообмена.
Задача 3.2-19 Необратимая экзотермическая реакция А > R + Qp с константой скорости, с-1, описываемой уравнением: k = 2,7•10 8 еxp(-7900/(T), проводится в каскаде из трех реакторов идеального смешения равных по объему 2 м 3 . Тепловой эффект реакции составляет 6,5•10 7 Дж/кмоль А, концентрация исходного реагента — 0,5 кмоль/м 3 . Теплоемкость реакционной смеси равна 2400 Дж/(кг•К), а плотность — 850 кг/м3 и не зависят от температуры. Реакционная смесь подается в реактор с температ (цена 200р) урой 5 °С и скорость 2•10 -3 м 3 /с.
Определить, какое количество теплоты надо подводить или отводить от каждого реактора, если в них поддерживать следующие температуры 15, 25, 35 °С.
Задача 3.2-20 Экзотермическая реакция А → R + Qp проводится в непрерывном реакторе идеального смешения, работающем в адиабатическом режиме. Тепловой эффект реакции равен 149 кДж/моль. Исходная концентрация вещества А составляет 0,25 молярной доли. Теплоемкость реакционной смеси постоянна и равна 2,2 кДж/(моль*К). Требуемая степень превращения вещества А составляет 0,95.
Определить температуру реакционной смеси на входе в реактор, если зависимость хА = f(T) представлена следующими данными:
Отвечает ли полученный результат устойчивому режиму работы реактора идеального смешения?
Видео:Тепловой эффект хим. реакции. Энтальпия. Закон Гесса. Капучинка ^-^Скачать

Реактор идеального смешения
Непрерывного действия
Схема потоков в реакторе полного смешения представлена на рис. 1. В реакторе такого типа концентрация любого компонента равномерна по всему реакционному объему, и поэтому уравнение материального баланса можно записать для всего объема реактора. Для установившегося режима:
где Gпр – масса вещества, поступающего в элементарный объем в единицу времени; Gух — масса вещества, выходящего из элементарного объема в единицу времени; Gхр – скорость расходования исходного вещества в результате химической реакции, протекающей в элементарном объеме:
 (2); (2);  (3). Так как степень превращения равна: (3). Так как степень превращения равна: 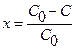 (4); (4); 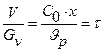 (5); то (5); то  (6), (6), |  Рис.1. Схема реактора идеального смешения. Рис.1. Схема реактора идеального смешения. |
где, 




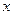
Уравнение (5, 6) представляют собой проектные уравнения реактора идеального смешения и позволяют определить неизвестную величину по заданным. В любом случае для реактора идеального смешения его размер, расход реагентов, начальные и конечные концентрации могут быть определены только при условии, если известна кинетика процесса.
В таблице 1 приведены расчетные уравнения для реактора идеального смешения непрерывного действия при проведении в нем простых обратимых и необратимых, а также сложных химических реакций.
Таблица 1. Расчетные уравнения для РИС-Н
| Схема реакции | Кинетическая модель | Расчетные уравнения |
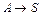 |  |    |
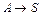 |  при при  | 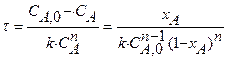 |
 |    |   |
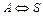 |   |    |
 |    |       |
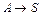  |  |   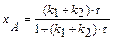 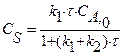  |
Рассмотрим некоторые примеры расчета такого типа реакторов.
Пример 1.
Определить объем реактора идеального смешения для реакции протекающего без изменения объема реакционной массы.
порядок реакции n=1;
объемный расход исходного вещества GV = 0,25 л/мин;
начальная концентрация исходного вещества СА0= 0,5 моль/л;
константа скорости реакции k= 0.15 мин -1 ;
степень превращения xA = 0,52.
Так как реакция первого порядка, скорость реакции определяем по уравнению:

В РИС-Н приравниваем объем реакционной массы к объему реактора, тогда по уравнению:
Пример 2.
Определить объем реактора идеального смешения для обратимой реакции протекающего без изменения объема реакционной массы.
порядок реакции n=2;
объемный расход исходного вещества GV = 4,8 м 3 /ч;
начальная концентрация исходного вещества СА,0= 1,5 кмоль/м 3 ;
константа скорости прямой реакции k1 = 2*10-3 м 3 /(кмоль∙с);
константа равновесия Кр = 9;
требуемая степень превращения xA = 0,8 от равновесной.
Объем реактора, в котором проводится данная реакция, определяем из базового уравнения для РИС-Н:
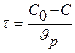

Так как реакция обратимая, составляем кинетическую модель для данной реакции:



С учетом вышеизложенного выражаем время реакции:
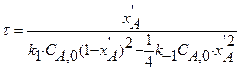
где 

В этом уравнении неизвестными величинами являются фактическая степень превращения и константа скорости обратной реакции. Константу скорости обратимой реакции определяем из уравнения:

Для определения равновесной степени превращения используем константу равновесия, выраженную через концентрации веществ:

где 
Подставляя в данное выражение значения константы равновесия, получаем 

Тогда время реакции будет равно:

С учетом полученного времени реакции объем реактора составит:
Пример 3.
Определить объем реактора смешения и достигаемую степень превращения вещества А при условии, что производительность (П) по продукту R составляет 4,8 кмоль/ч.
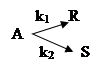
объемный расход исходного вещества GV = 100 л/мин.;
начальная концентрация исходного вещества СА0= 1,6 моль/м 3 ;
константа скорости прямой реакции k1 = 0,28 л/(моль*мин.);
константа скорости обратной реакции k2 = 0,12 л/(моль*мин.).
По заданной производительности определяем концентрацию по продукту R. Для этого переведем производительность в моль/мин.
Скорость изменения концентрации продукта R в реакторе смешения можно выразить так:


Из базового уравнения для РИС-Н получаем:

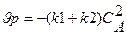
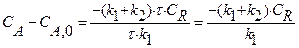

Определяем степень превращения по уравнению:
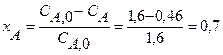
Определяем время пребывания исходя из базового уравнения:
Определяем объем реактора:

Пример 4.
Рассчитать объем реактора смешения для получения максимального количества продукта R, а также определить селективность и производительность по продукту R.
Реакция: А → R → S
объемный расход исходного вещества GV = 18м 3 /ч;
начальная концентрация исходного вещества СА0= 4,8 моль/л;
константа скорости прямой реакции k1 = 5мин -1 и k2 = 1,8мин -1 .
Для получения максимального количества продукта R необходимо выводить реакционную массу из реакционной зоны в момент, когда концентрация вещества R максимальна, что соответствует оптимальному времени пребывания в реакционной зоне.
Из базового уравнения для реактора смешения для продукта R запишем выражение:




Оптимальное время пребывания реакционной массы в зоне реакции определяем по формуле (см. таб.1).
Рассчитываем степень превращения вещества А по формуле (см. таб. 1.):

Определяем концентрацию R на выходе из реактора:

Определяем производительность по продукту R.
Рассчитываем объем реактора смешения:
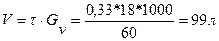
Определяем селективность по продукту R:

Задачи для самостоятельного решения
1. Жидкофазная реакция типа А → 2S имеет константу скорости, равную 4.5 ч -1 .Объемный расход исходного вещества с концентрацией 0.8 моль/л составляет 14,5 м 3 /ч. Рассчитать суточную производительность по продукту R для реактора идеального смешения объемом 3 м 3 .
2. В непрерывном реакторе смешения проводится последовательная реакция типа А→R→S с константами скоростей к1=0,5 ч -1 и к2=0,8 ч -1 . Исходная концентрация вещества А равна 5 кмоль/м 3 . Продукты R и S на входе в реактор отсутствуют. Рассчитать необходимый объем реактора смешения для максимального выхода целевого продукта R, степень превращения исходного реагента, селективность и выход по целевому продукту, если объемный расход составляет 2,4 м 3 /ч.
3. Процесс описывается последовательной реакцией типа А→R→S с константами скоростей к1=0,12 л/(моль/мин) и к2 = 0,8 л/(моль/мин). Объемный поток вещества А равен 3,6 м 3 /ч. Концентрация вещества А на входе в реактор составляет 3,4 моль/л, а степень его превращения – 0,48. Определить концентрации веществ R и S на выходе из реактора и объем реактора смешения.
4. Процесс описывается последовательной реакцией типа А→R→S с константами скоростей к1= 0,24 л/(моль/мин) и к2 = 0,18 л/(моль/мин). Объемный поток вещества А равен 3,6 м 3 /ч. Процесс проводится в реакторе смешения объемом 240 л. Концентрация вещества А на входе в реактор составляет 3,4 моль/л. Определить концентрации всех веществ на выходе из реактора, степень превращения вещества A и селективность по продукту R.
5. Процесс описывается последовательной реакцией типа А→R→S с константами скоростей k1= 0,18 л/(моль/мин) и k2 = 0,06 л/(моль/мин). Объемный поток вещества А равен 40 л/мин. Процесс проводится в реакторе смешения объемом 260 л. Концентрация вещества А равно 2,4 моль/л. Определить производительность реактора по продукту R, степень превращения вещества A и селективность по продукту R.
6. 
с константами скоростей k1= 0,18 л/(моль/мин) и k2 = 0,06 л/(моль/мин). Объемный поток вещества А равен 40 л/мин. Процесс проводится в реакторе смешения объемом 250 л. Концентрация вещества R на выходе из реактора равно 1,2 моль/л. Определить концентрацию вещества А на входе в реактор и степень превращения вещества A.
7. 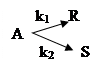
с константами скоростей k1= 0,28 л/(моль/мин) и k2 = 0,12 л/(моль/мин). Поток вещества поступает с концентрацией 1,6 моль/л. Процесс проводится в реакторе смешения объемом 200 л. Степень превращения вещества A составляет 0,8. Определить допустимый расход вещества А.
8. 
с константами скоростей k1= 0,28 л/(моль/мин) и k2 = 0,12 л/(моль/мин). Поток вещества поступает с концентрацией 1,6 моль/л. Процесс проводится в реакторе смешения объемом 140 л. Степень превращения вещества A составляет 0,7. Определить производительность реактора по продукту R.
9. 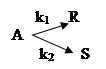
с константами скоростей k1= 0,28 л/(моль/мин) и k2 = 0,12 л/(моль/мин). Объемный поток вещества А с концентрацией 1,6 моль/л равен 100 л/мин. Процесс проводится в реакторе смешения. Определить объем реактора и достигаемую в нем степень превращения вещества А при условии, что производительность по продукту R составляет 4,8 кмоль/ч.
10. Процесс описывается реакцией типа А + В → R с константой скорости к = 0.28 л/(моль/мин). Объемные потоки вещества А с концентрацией 1,6 моль/л и вещества В с концентрацией 2,0 моль/л равны 100 л/мин. Процесс проводится в реакторе смешения объемом 1,2 м 3 . Концентрация вещества А на входе в реактор составляет 3,4 моль/л. Определить производительность реактора по продукту R.
11. Процесс описывается реакцией типа А + В → R с константой скорости к = 0,54 л/(моль/мин). Объемные потоки вещества А с концентрацией 1,8 моль/л и вещества В с концентрацией 2,7 моль/л равны 100 и 80 л/мин. Производительность реактора по продукту R составляет 8,64 кмоль/ч, концентрация продукта R на выходе — 0,8 моль/л. Определить требуемый объем реактора смешения
12. Процесс описывается реакцией типа 2А → R с константой скорости к = 0,64 л/(моль/мин). Заданная степень превращения вещества А составляет 0,8, исходная концентрация вещества А -1,8 кмоль/м 3 , производительность реактора по продукту R – 3,8 кмоль/ч. Определить требуемый объем реактора смешения.
13. Процесс описывается реакцией типа А → 2R с константой скорости к = 0,24 мин -1 . Заданная степень превращения вещества А составляет 0,8, исходная концентрация вещества А — 1,8 кмоль/м 3 , производительность реактора по продукту R – 5,8 кмоль/ч. Определить требуемый объем реактора смешения и объемный расход исходной смеси.
14. Процесс описывается обратимой реакцией первого порядка типа 2А 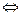
🌟 Видео
Химические уравнения - Как составлять уравнения реакций // Составление Уравнений Химических РеакцийСкачать

Как выучить Химию с нуля за 10 минут? Принцип Ле-ШательеСкачать

Химические реакции в природе и жизнедеятельности живых организмов. 8 класс.Скачать

Химическая кинетика. Скорость химической реакции | ХимияСкачать

Основы химической термодинамикиСкачать

25. Схема реакции и химическое уравнениеСкачать

Реакции присоединения | Химия 10 класс | УмскулСкачать

Влияние концентрации на скорость химических реакций. 10 класс.Скачать

Влияние температуры на скорость химических реакций. 10 класс.Скачать

Химия Лекция №1 Термодинамика и кинетика химических процессовСкачать

Все о скорости химической реакции | Химия ЕГЭ 10 класс | УмскулСкачать

ЛЕКЦИЯ №1 || Химическая кинетика || Основные понятия, элементарный акт, стехиометрическое уравнениеСкачать

Скорость химической реакцииСкачать

Определение порядка реакции методом подбора кинетического уравненияСкачать

Свободная энергия Гиббса и самопроизвольные реакции (видео 8) | Энергия| БиологияСкачать

Энергетика химических процессов, 1976Скачать