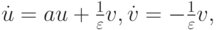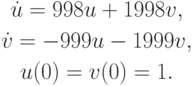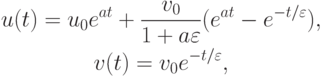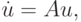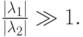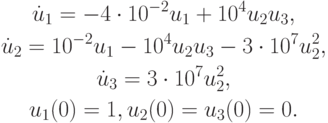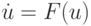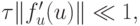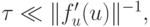Жесткой системой обыкновенных дифференциальных уравнений

9.1. Явление жесткости. Предварительные сведения

Рассмотрим в качестве примера две задачи Коши для систем обыкновенных дифференциальных уравнений (ОДУ) [9.1], [9.2]:

с начальными данными u(0) = u₀, v(0) = v₀ ; здесь 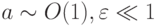; и линейную систему с постоянными коэффициентами

Решением первой задачи Коши являются функции

В обоих случаях решение состоит из двух экспонент: быстро убывающей и относительно медленно изменяющейся. Отметим, что абсолютные величины собственных значений матриц рассматриваемых линейных систем ОДУ при их представлении в виде

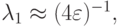
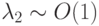
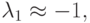
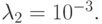
( u — вектор — столбец, A — матрица с постоянными коэффициентами) существенно различаются. Так, в первом случае ; во втором: В обоих случаях имеем:

При моделировании физических процессов причина такой разницы в собственных числах заключена в существенно различных характерных временах процессов, описываемых системами ОДУ. Наиболее часто подобные системы встречаются при моделировании процессов в ядерных реакторах, при решении задач радиофизики, астрофизики, физики плазмы, биофизики, химической кинетики. Последние задачи часто могут быть записаны в виде [9.3]:

где u_k — концентрации веществ, участвующих в химических реакциях, скорости протекания которых характеризуются коэффициентами 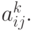В качестве примера приведем одну из систем химической кинетики, описывающую изменение концентрации трех веществ, участвующих в реакции для случая полного перемешивания [9.1].

Пример 1. Обозначим концентрации трех веществ, участвующих в реакции, через u₁ , u₂ и u₃ , тогда

Участки решения, характеризующиеся быстрым и медленным его изменением, называются пограничным слоем и квазистационарным режимом, соответственно.

Трудности численного решения подобных систем ОДУ , получивших название жестких ( определение жесткой системы приведено ниже), связаны с выбором шага интегрирования. Дело в том, что характерные времена исследуемых процессов могут различаться более чем в 10 12 раз. Следовательно, если при численном решении системы

выбирать шаг из условия

то он будет соответствовать самому быстрому процессу. В данном случае затраты машинного времени для исследования самых медленных процессов будут неоправданно велики. По этой причине имеются следующие альтернативы в выборе подхода к численному решению рассматриваемых задач.

1. Численно решать систему ОДУ с шагом

т.е. с учетом характерных времен всех процессов, описываемых данной системой.

Видео:Лекция Системы обыкновенных дифференциальных уравненийСкачать

Жесткой системой обыкновенных дифференциальных уравнений

В вычислительной практике часто встречаются системы дифференциальных уравнений, которые принято называть жесткими.
Не приводя точного определения жесткой системы, проиллюстрируем содержание этого понятия и возникающие проблемы на примере жесткой линейной системы двух дифференциальных уравнений с постоянными коэффициентами.

Пусть требуется численно решить задачу Коши
y‘₁ = -2y₁ — 998 y₂ ,
y‘₂ = — 1000y₂ ,
y₁ (0) = 2, y₂ (0)=1.
Эту задачу можно записать в матричной форме в виде:

где

искомое решение,

матрица системы,

значение решения в начальной точке x = 0 — начальное условие.

Легко видеть, что точное решение системы имеет вид:
y₁ (x) = exp(-2x) + exp(-1000x),
y₂ (x) = exp(-1000x).
Слагаемое
exp(-1000x)
убывает очень быстро,
а слагаемое exp(-2x) — гораздо медленнее.

Попытаемся найти решение этой задачи методом Рунге-Кутты с различными шагами. Графики полученных решений и графики точного решения приведены ниже (график точного решения — справа).

Видно, что полученные приближенные решения уже на первых шагах содержат большие ошибки. Для получения правдоподобного результата на отрезке [0, 0.1] нужно выбирать шаг, меньший 0.003. Это означает, что для достаточно большого интервала интегрирования потребуется выполнить вычисления для очень большого числа шагов. Казалось бы, можно избежать интегрирования на всем промежутке с малым шагом: вести вычисления с малым шагом до тех пор, пока компонента
exp(-1000x)
станет пренебрежимо малой, а затем увеличить шаг и до конца промежутка интегрирования вести вычисления с большим шагом. Оказывается, что на самом деле это совсем не так. Вторая компонента заставляет вести интегрирование с малым шагом на всем промежутке интегрирования. Это и означает, что система жесткая. Жесткость системы проявляется тогда, когда длина промежутка интегрирования T удовлетворяет соотношению
где l _max — наибольшее по абсолютной величине собственное число матрицы системы A. Для интегрирования жестких систем необходимо применять специально разработанные методы.

ПРИМЕР 1. Интегрирование жесткой системы дифференциальных уравнений.

В примере рассмотрена линейная жесткая система. Однако специальные методы решения жестких систем, как правило, универсальны, т.е. применяются для решения как линейных так и нелинейных систем.

Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter

Видео:Решение системы дифференциальных уравнений методом ЭйлераСкачать

Научная статья на тему: «Жесткие системы дифференциальных уравнений»

1 ЖЕСТКИЕ СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ

Понятие жесткой линейной системы дифференциальных уравнений

Задачи, называемые жесткими, весьма разнообразны, и дать математически строгое определение жесткости непросто[15]. Поэтому в литературе можно встретить различные определения жесткости, отличающиеся степенью строгости.

Приведем определения различных авторов.

Определение 1. Система дифференциальных уравнений [3]

с постоянной матрицей называется жесткой, если выполняются следующие условия:

1) (здесь — действительная часть собственного значения );

2) велико отношение

Число S называется числом жесткости системы. Однако величина , начиная с которой система становится жесткой, не указывается, она определяется конкретной физической постановкой задачи.

Если матрицас переменными коэффициентами, то есть зависит от , то ее собственные числа являются функциями — . При каждом можно определить число жесткости

которое также зависит от . В этом случае система уравнений

с матрицей, зависящей от , называется жесткой на интервале, если , для всех и число велико.

Сущность явления жесткости состоит в том, что решение, которое нужно вычислить, меняется медленно, однако существуют быстро затухающие возмущения. Наличие таких возмущений затрудняет получение медленно меняющегося решения численным способом.[2]

Рассмотрим как связана жесткость системы [2]

_{с жесткостью неоднородной системы}

_{Решение неоднородной системы может быть записано в виде}

где — нормированная фундаментальная матрица однородной системы;
— частное решение неоднородной системы. Пусть неоднородная система жесткая. Тогда требование жесткости

должно выполняться при любых начальных условиях Где

— максимальный модуль собственных чисел матрицы Якоби, — точка, отделяющая пограничный слой (переходной участок). Малая продолжительность пограничного слоя по сравнению с полным отрезком наблюдения задается неравенством а значения производных вне пограничного слоя полагаются меньшими, чем значения внутри него, в раз, где

Выбирая в частном случае убеждаемся, что условие жесткости должно выполняться не только для самого вектора , но и для обоих слагаемых неоднородной системы по отдельности. А так как первое слагаемое является решением однородной системы, то эта однородная система должна быть жесткой.

Таким образом, из жесткости неоднородной системы следует жесткость однородной. Это утверждение свидетельствует о том, что жесткость является внутренним свойством линейной системы и не может появиться только благодаря изменениям функции

_{Все рассуждения остаются в силе и для того случая, когда матрица имеет переменные коэффициенты.}

Определение 2. Рассмотрим линейную задачу общего вида [15]

где — постоянная матрица , — зависящая от времени функция.

Наиболее очевидный способ определения жесткости для этой линейной системы заключается в наложении условий на собственные значения матрицы . Обозначим эти собственные значения . Тогда задачу можно назвать жесткой, если:

1° Существуют для которых .

2° Существуют умеренной величины, то есть „мало» по сравнению с абсолютными величинами собственных значений, удовлетворяющих условию 1°.

3° Не существует с „большой» положительной вещественной частью.
4° Не существует с „большой» мнимой частью, для которого не выполняется условие.

Очевидно, что эти условия, наложенные на спектр матрицы А,
подразумевают, что линейная задача вида

жесткая задача в вышеописанном смысле вне переходного участка, определяемого быстро затухающими экспонентами. Здесь предполагается, что функция обладает той же гладкостью, как и медленно меняющиеся экспоненты в решении.

Если —негладкая функция (например, в некоторый момент времени она претерпевает резкое изменение, которое почти является разрывом на временном масштабе медленно меняющихся экспонент), то задача может измениться от жесткой к нежесткой. Следует заметить, что условия не исключают неустойчивых задач, т. е. допускается . Конечно, надо потребовать, чтобы быстро изменяющиеся решения были устойчивыми. Многие авторы требуют, чтобы для всех выполнялось условие .

Однако это требование излишне. Условие 4° добавлено для того, чтобы исключить сильно осциллирующие задачи. Подобные задачи требуют специального рассмотрения и не могут эффективно решаться существующими методами, предназначенными для жестких задач. Жесткость имеет место тогда, когда искомое решение носит гладкий характер, т. е. медленно меняется, в то время как малые погрешности приводят к возмущениям, которые быстро затухают. При дискретизации жесткой задачи численный метод должен быть в состоянии подавить эти возмущения подобно тому, как это происходит в дифференциальном уравнении.

Определение 3. Рассмотрим простейшее линейное однородное уравнение 1-го порядка [16]:

и задачу Коши для (1.1.1):

Решение (1.1.1) – (1.1.3), очевидно,

Если , имеем неограниченное (неустойчивое) решение (рис.1.1.1). В этом случае надо просто интегрировать (1.1.1) с шагом по времени, обеспечивающим необходимую точность, до тех пор, пока это возможно.

Рис.1.1.1. Рис.1.1.2. Рис.1.1.3.

Если , то решение задачи (1.1.1) – (1.1.3) ограниченное (). С точки зрения вычислителя здесь важна величина отрезка интегрирования T .

Если , то имеем обычную ситуацию (рис.1.1.2), можно пользоваться стандартными методами численного интегрирования (Эйлера, Эйлера–Коши, Рунге–Кутты, Адамса и т. д.).

Если , то имеем решение типа «пограничного слоя» (рис.1.1.3) с резким изменением на малом (в масштабе T ) отрезке .

Если положение «пограничного слоя» заранее неизвестно, при численном интегрировании возникают осложнения, которые будут рассмотрены ниже. Основная идея заключается в том, чтобы численный метод обеспечивал качественно правильное поведение численного решения на участке «пограничного слоя» (при ), т. е. быстрое затухание, и возможно точнее воспроизводил решение на основном участке интегрирования (вне «пограничного слоя»).

Определение 4. Жесткие системы уравнений — это такие уравнения, которые моделируют процессы, обладающие явлением жесткости [17].

Определение 5. Задачу Коши [1 0 ]

будем называть жесткой, если спектр матрицы достаточно четко делится на две части.

Жесткий спектр. Собственные значения и векторы обозначим и .
_{Для жесткого спектра выполняются условия}

Мягкий спектр. Собственные значения и векторы обозначим и .
_{Для мягкого спектра выполняются условия}

Время интегрирования является средним относительно и очень большим относительно : равно, например, , а может быть порядка ,и больше. Отношение называют показателем жесткости системы.[3]
Определение 6. Наиболее прагматическая точка зрения вместе с тем была и исторически наиболее ранней (Кертисс и Хиршфельдер 1952): жесткие уравнения — это уравнения, для которых определенные неявные методы, дают лучший результат, обычно несравненно более хороший, чем явные методы. При этом определенную роль играют собственные значения матрицы Якоби , но важны и такие параметры, как размерность системы, гладкость решения или интервал интегрирования [11].

Жесткие уравнения — это задачи, для которых явные методы не работают.

Кертисс и Хиршфельдер объясняют свойство жесткости на одномерных примерах, таких, как уравнение [11]

Для решения данного уравнения применяется явный метод Эйлера. У д анно г уравнени я вблизи имеется медленно изменяющееся решение, а все другие решения подходят к нему после быстрой «переходной фазы». Такие быстрые переходы типичны для жестких уравнений, но не являются ни достаточным, ни необходимым признаком. Как только длина шага становится больше критической величины (в данном случае больше ), численное решение уходит слишком далеко за равновесное, и возникают все более сильные колебания. Применение неявного метода Эйлера демонстрирует устойчивость этого метода.

Рассмотрим вначале скалярное уравнение [15]

где — медленно меняющаяся функция только от _.

Решение имеет вид

или, если связать решение в момент времени с решением в момент

Так както ясно, что уже после очень небольшого отрезка времени
переходная часть решения , которая также называется жесткой компонентой решения или сильно меняющейся компонентой, в больше не присутствует. Это означает, что независимо от начального значенияв численном решении на большей части отрезка интегрирования преобладает медленно меняющаяся функция . Второе выражение для решения показывает, что существующие в любой момент времени возмущения медленно меняющегося решения быстро затухают. Заметим также, что медленно меняющиеся компоненты решения часто называют непереходными или гладкими компонентами. Термин «гладкие» используется в том смысле, что производные от этих компонент решения значительно меньше производных от переходных компонентов.

Рассмотрим жесткую систему дифференциальных уравнений [6]

_{решение, которой записывается в виде}

Каждая компонента решения содержит как «медленную», так и «быструю» составляющую. «Быстрая» составляющая лишь в малой окрестности начальной точки вносит существенный вклад в решение. Затем поведение функций определяется в основном функцией . Тем не менее при численном интегрировании этой системы ограничение на величину шага накладывает именно составляющая .

Рассмотрим уравнение [15]

где матрица задана следующим образом:

Собственные значения этой зависящей от времени матрицы размера постоянны и равны соответственно , но решением служит функция

где — константы. Этот пример принадлежит Винограду[15]. Пример Винограда можно назвать умерено жестким.

Обобщим пример Винограда [15] и составим задачу, которую можно сделать произвольной жесткости, сохраняя при этом типичное поведение решения.

Рассмотрим задачу [15]

где — константы. Сделаем замену переменной

Новая независимая переменная удовлетворяет уравнению

Собственные значения постоянной матрицы , которые определяют экспоненциальное поведение решения , удовлетворяют характеристическому уравнению

В случае получаем уравнение Винограда с собственными значениями.

1.2 Понятие жесткой нелинейной системы дифференциальных уравнений

Определение 7. Система дифференциальных уравнений [2]

называется жесткой на отрезке изменения независимой переменной , принадлежащем интервалу существования ее решений, если при любом векторе начальных значений и на любом отрезке найдутся такие числа удовлетворяющие

где — максимальный модуль собственных чисел матрицы Якоби, что справедливы неравенства

Если начальные условия таковы, что пограничный слой, явно присутствует, то величина дает представление о том, во сколько раз уменьшилось производные после его прохождения.

Важным моментом определения является неразрывная связь жесткости системы с величиной промежутка наблюдения решения .

Если жесткую на систему рассматривать лишь на промежутке включающем только пограничный слой то на ее нельзя считать жесткой, так как никакого различия в характере поведения решения не наблюдается.

Определение 8. Рассмотрим нелинейную задачу[15].

В нелинейной задаче жесткость обычно описывается довольно нестрогим образом в терминах собственных значений матрицы Якоби

вдоль кривой точного решения. Если условия

1° Существуют для которых .

2° Существуют умеренной величины, то есть „мало» по сравнению с абсолютными величинами собственных значений, удовлетворяющих условию 3°Не существует с „большой» положительной вещественной частью.
4° Не существует с „большой» мнимой частью, для которого не выполняется условие.

Определение жесткости, приемлемое для линейных систем с постоянными коэффициентами, распространяется на случай нелинейных систем и линейных систем с переменными коэффициентами. Однако, как указывал Ламберт, подобное определение для последних двух классов задач является недостаточно точным. Слабое место в обобщении определения состоит в том, что спектр «замороженной» матрицы Якоби в уравнении не дает правильной информации о качественном поведении решения уравнения.

Рассмотрим одно сингулярно-возмущенное уравнение [11]:

Рис.1.2.1. Поле решений уравнения (1.2.1)

Если предельное (вырожденное) уравнение (1.2.1) приимеет вид

при каждом значении t имеет единственное решение

и в окрестности этого предельного решения (условие устойчивости решений (1.1.2)), , то имеем ситуацию, изображенную на рис.1.2.1.
Как и в линейном случае, поведение решения разделяется на два характерных участка: пограничный слой для малых (его длина ), и близкое к предельному решению (1.1.2) поведение при.
Обычно определяемый «физикой задачи» участок интегрирования .

Рассмотрим автономную (правая часть не зависит от времени) систему двух нелинейных уравнений [18]:

Убедимся, что система жесткая. Записав (1.2.3) в векторной форме

Если мало, то , . Видно, что , при (λ ₂ называют нормальной частью спектра, а λ ₁ — жесткой частью спектра).

В случае уравнения Ван-дер-Поля:

получаем предельное уравнение и поле решений в фазовой плоскости, изображённое на рис.1.2.2.

Рис.1.2.2. Поле решений уравнения Ван-дер-Поля

Вдали от линии имеем почти горизонтальное поле направлений , а на линии выделяются две устойчивые ветви AB и CD и одна неустойчивая ветвь BC . При любых начальных значениях траектория этой системы — замкнутая кривая BB΄CC΄ .

1) На участке траектория почти горизонтальна и приближенно определяется уравнениями:

2) При и система описывается предельными уравнениями (1.2.5) (квазистационарный режим вплоть до точки B ). Если и после т. B пользоваться предельными уравнениями (1.2.5), то мы бы двигались по BC . Но реальная система на этом участке является неустойчивой и сходит с него на ветвь DB΄C . На этом участке , и решение определяется поведением.

3) Опять пограничный слой (1.2.6) при, за ним квазистационарное движение на участке B΄C при, пограничный слой и т. д. (все повторяется).

Рис.2.1.3. Компоненты решения уравнений Ван-дер-Поля в зависимости от времени

В случае задачи Коши для общей нелинейной системы

поведение ее решения вблизи некоторой точки определяется матрицей Якоби :

Система называется жесткой, если для всех ( т. е. на решениях (1.2.7)), собственные значения матрицыудовлетворяют условиям[16]:

Для оценки можно взять легко вычисляемую величину нормы
матрицы, для оценки — величину следа матрицы; можно заменить на величину, определяемую обычно из физики задачи.

То есть простейшим критерием жесткости системы могут служить неравенстваТ||A|| > 1, (иногда ограничиваются одним условием ). Однако надежных простых способов определения жёсткости нет, и поэтому нужны численные методы, работающие без проверок на жесткость.

Модель Филда–Нойса «орегонатор» [19]. Простейшая модель периодической химической реакции Белоусова–Жаботинского состоит из трех уравнений:

На то, что система жесткая, указывают большие различия в константах скоростей реакций — есть процессы «быстрые», и есть «медленные».

Так как переменные системы — концентрации ( HBrO ₂ , Br – и Ce ( IV ) соответственно), то начальные условия для системы следует выбирать положительными. Как правило, их выбирают достаточно близкими к 0. Время интегрирования системы.

Уравнение Ван-дер-Поля [20]. Типичным примером жесткой задачи малой размерности является уравнение Ван-дер-Поля. Его возможно записать в виде системы

(представление Льенара). Считаем, что параметр a — большой. В расчетах рассматриваются два случая: a = 10 3 или a = 10 6 . Обычно полагают Время интегрирования системы .

Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Пример 1.7.

Видео:Видеоурок "Системы дифференциальных уравнений"Скачать

Система Ван-дер-Поля и траектории-утки [21]. Рассмотрим неавтономную систему Ван-дер-Поля:

Как и в предыдущей задаче считаем, что a = 10 3 или a = 10 6 ,

Время интегрирования системы.

Видео:Лабораторная работа 1. Решение систем обыкновенных дифференциальных уравненийСкачать

Пример 1.8.

Видео:Поле направлений дифференциального уравнения первого порядкаСкачать

Суточные колебания озона в атмосфере [22]. Рассмотрим простейшую математическую модель колебаний концентрации озона в атмосфере. Она описывается следующей неавтономной системой ОДУ:

В данной модели уравнения описывают изменение концентрации атомарного кислорода, молекулярного кислорода и озона соответственно. Считается, что изменения концентрации молекулярного кислорода невелики. Начальные значения для задачи таковы: (см –3 ), (см –3 ), (см –3 ), а значения констант скоростей химических реакций , .

Две другие химические реакции зависят от локальной освещенности участка земной поверхности и приближаются следующим выражением:

где с –1 , с ₃ = 22,62, с ₄ = 7,601. Значения констант скоростей обращаются в ноль «ночью», резко возрастают «на рассвете», достигают максимума «в полдень» и падают до ноля «на закате». Время интегрирования . Данная система является жесткой «ночью» и умеренно жесткой «в светлое время суток».

Видео:Кобельков Г. М. - Численные методы. Часть 2 -Жесткие системы обыкновенных дифференциальных уравненийСкачать

Пример 1.9.

Видео:Дифференциальные уравнения, 1 урок, Дифференциальные уравнения. Основные понятияСкачать

Уравнение Бонгоффера–Ван-дер-Поля [20]. Рассмотрим еще один пример жесткой задачи малой размерности, имеющей периодическое решение:

Здесь a = 10 3 , Уравнение описывает протекание тока через клеточную мембрану. Постоянная компонента тока c в безразмерной записи системы такова, что 0 c b > 0. Время интегрирования системы.

Видео:Откуда появляются дифференциальные уравнения и как их решатьСкачать

Пример 1.10.

Видео:Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Сингулярно-возмущенная система — модель двухлампового генератора Фрюгауфа [23]. Система более высокой размерности, имеющая решение в виде релаксационного цикла имеет вид:

Здесь α > 0 порядка 1, функция ε = 10 –3 , 10 –6 . Время интегрирования

Простейшая модель гликолиза описывается уравнениями следующего вида [23]:

предложенными Дж. Хиггинсом. В системе β = 10, α = 100, 200, 400, 1000. Начальные условия для системы: y ₁ (0) = 1, y ₂ (0) = 0,001. Решение этой системы — релаксационные автоколебания (жесткий предельный цикл). Время интегрирования системы

Видео:7. Линейные дифференциальные уравнения первого порядка. Метод Бернулли.Скачать

Пример 1.12.

Видео:Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

Модель химических реакций Робертсона один из первых и самых популярных примеров «жесткой» системы обыкновенных дифференциальных уравнений принадлежит Робертсону (1966) имеет вид [11]:

Начальные условия для системы таковы: y ₁ (0) = 1, y ₂ (0) = 0, y ₃ (0) = 0. Время интегрирования системы

Модель дифференциации растительной ткани — типичный случай биохимической модели «умеренной» размерности (современные модели, например, фотосинтеза включают сотни уравнений подобного типа) [11]. Хотя данная модель является умеренножесткой, тем не менее, ее лучше решать с помощью методов, предназначенных для решения жесткой системы дифференциальных уравнений.

Начальные значения всех переменных системы равны 0, кроме y ₁ (0) = 1 и y ₈ (0) = 0,0057.Время интегрирования системы

Видео:Системы дифференциальных уравненийСкачать

Пример 1.14.

Видео:Устойчивость 1 ОпределениеСкачать

Еще одна модель химической реакции, получившая свое название Е5 [11]:

Начальные условия: y ₁ (0) = 1,76·10 –3 , а все остальные переменные равны 0. Значения коэффициентов модели следующие: A = 7,89·10 –10 , B = 1,1·10 7 , C = 1,13·10 3 , M = 10 6 . Время интегрирования системы

Уравнение Релея во многом похоже на уравнение Ван-дер-Поля. Рассматривается задача вида [23]

Начальные условия: x (0) = 0, μ = 1000. Время интегрирования системы

Экогенетические модели. Рассмотрим пример системы уравнений, которая описывает изменения численности популяций двух видов и эволюцию некого генетического признака α . Система имеет вид [24]:

Параметры задачи таковы: ε ≤ 0,01, 0 ≤ x ₀ ≤ 3, 0 ≤ y ₀ ≤ 15, α ₀ = 0,01.Время интегрирования системы. Наличие малого параметра в третьем уравнении системы показывает, что генетический признак меняется медленнее, чем численность популяций. Решение системы — релаксационные колебания.

Наряду с данной задачей приведем пример более интересной: численность двух популяций зависит от их взаимодействия и двух медленно меняющихся генетических признаков.

Параметры задачи таковы: ε ≤ 0,01, 0 ≤ x ₀ ≤ 40, 0 ≤ y ₀ ≤ 40, α ₁₀ = 0, α ₂₀ = 10. Время интегрирования системы . Рассмотреть также модификацию предыдущей системы [24]:

Параметры задачи: ε ≤ 0,01, 0 ≤ x ₀ ≤ 40, 0 ≤ y ₀ ≤ 40, α ₁₀ = 0, α ₂₀ = 10. Время интегрирования .

1.3 Методы решения жестких систем дифференциальных уравнений

Создание численных методов решения жестких систем в большинстве случаев основано на идеях, представленных Хайрером и Ванером [11]. В своей работе они постулировали, что жесткие системы не могут быть решены явными методами, и представили подходы, основанные только на использовании неявных методов. Однако, следует отметить, что непосредственное применение этих методов всегда связано с крайне сложной процедурой определения параметров схемы, основанной на заранее выделенной области устойчивости только для рассматриваемой системы. Это обстоятельство делает предложенные подходы не приемлемыми для большинства вышеуказанных приложений, но позволяет выделить два важных математических свойства жесткости. Во-первых, все жесткие системы обладают очень широким спектром (или присутствием очень разных экспонент Ляпунова). Во-вторых, согласно теореме единственности и существования решения, для жестких систем характерны большие значения константы Липшица.

Для решения жестких систем дифференциальных обыкновенных уравнений существуют различные методы, например, методы Рунге- Кутты, методы Розенброка, Булиша- Шера, Радо, Лобатто.

В случае жестких обыкновенных дифференциальных уравнений предъявляются обычно следующие требования к численному методу: согласованность (схема должна аппроксимировать обыкновенные дифференциальные уравнения); соответствие специальным требованиям устойчивости; необходимость пройти ряд вычислительных текстовых задач.

При численном решении задач с помощью разностных схем в некоторой последовательности точек вычисляются значения . Одношаговые (двухточечные) методы типа Рунге–Кутты (схемы с пересчетом или схемы предиктор-корректор) наиболее популярны. Многие неявные варианты этих схем пригодны и для жестких систем. Для вычисления требуется знание только . Для неявных вариантов методов типа Рунге–Кутты косвенно используется матрица Якоби (несущая информацию о свойствах системы). В этих методах легко меняется шаг интегрирования в необходимых случаях. Могут быть построены методы достаточно высокого порядка точности. Вместе с тем требуется многократное вычисление правой части в промежуточных точках , которые при переходе к новой точке не используются.

Многошаговые линейные методы (тоже могут быть и явными и неявными). При использовании этих методов не пропадает впустую информация в предыдущих точках , т.е. эти методы требуют меньшего числа вычислений . Как и в одношаговых методах, в случае неявных схем косвенно используется информация о матрице Якоби. Однако эти методы требуют “разгона” (вычисления дополнительных “начальных” значений в точках, получаемых другими методами). Для явных схем возникают трудности с изменением шага интегрирования в процессе счета.

Не очень распространенный, но перспективный (в том числе для жестких систем) подход, связанный с переходом к продолженным системам:

Вводя расширенный искомый вектор , получаем для него уравнение

(, если явно не зависит от , то есть в случае автономной системы). Увеличивая размерность (т.е. вычисляя в точках t= t n не только v, v_t = f, но и и т.д.), этот процесс можно продолжить (конечно, еслизадается аналитически и соответствующие производные отне очень громоздки).

Каким же условиям должны удовлетворять разностные схемы для решения жестких систем? Разберем на примере системы

два простейших метода – явный и неявный методы ломаных, называемые также схемами Эйлера.

На участке пограничного слоя (его протяженность ) для воспроизведения решения пригоден практически любой обеспечивающий необходимую точность численный метод с шагом . Например, даже для явной схемы Эйлера в линейном случае

имеем из условия устойчивости . Для примера (1.3.2), уравнения Ван дер Поля , что не является здесь обременительным. Общее число шагов по времени

10÷100 тоже вполне приемлемо. Однако это ограничение на шаг интегрирования действует и на участках квазистационарного решения (С΄B, B΄C) на рис.1.3.1 и для прохождения таких участков потребуется уже шагов! А это уже неприемлемо при очень малых . Возможный выход – переход к решению предельной системы (1.2.4) , в которой уже не фигурирует, а условие устойчивости (конечно, линеаризованное, т.е. действующее в небольшой окрестности кривой C΄BB΄CC΄) или вполне приемлемо.

При численном решении на участках С΄B и BС΄ рис.1.3.1 полной системы (1.2.3), (1.2.5) хорошо работает неявный метод Эйлера

Для решения, получающейся на каждом шаге по t нелинейной относительно v n+1 системы

используется какой-либо итерационный метод (например, метод Ньютона).

В случае линейной системы в неявном методе Эйлера

условие устойчивости выполняется для любых при . Поэтому при использовании метода (1.3.4) для задачи (1.2.3), (1.2.5) на участках С΄B, BС΄ нет проблем, исключая, конечно, тот факт, что матрица A плохо обусловлена для жестких систем и при обращении матрицы (E–A) могут возникнуть трудности при больших . Проведённый анализ показывает, (да и просто по графику x(t) на рис. 1.3.1 видно), что шаг интегрирования на разных участках следует выбирать разным, и численный метод должен позволять это делать достаточно просто. Это первая характерная особенность жестких систем. То есть надо уметь предсказывать момент появления пограничных слоев, а это определяется собственными значениями матрицы Якоби. Отметим также, что в неявном методе Эйлера для системы (1.2.3)

т.е. приближенно мы как бы решаем предельную систему (1.2.4), так как

Менять шаг интегрирования в процессе счета можно, но далеко не всегда нас интересует детальное поведение решения в пределах пограничного слоя. В таких случаях можно брать и по неявной схеме проходить пограничный слой за один шаг по времени.

Посмотрим еще, что будет происходить в неявной схеме вблизи точки B (или С) на примере уравнения Ван дер Поля (1.2.3), (1.2.5). Имеем:

Вблизи точки B с координатамиимеем

т.е. кубическое относительно искомого уравнение, решения которого изображены на рис. 1.3.1.

Рис. 1.3.1. К алгоритму расчета уравнения Ван-дер-Поля по неявной схеме Эйлера

Выбор в итерационном методе в качестве начального приближенияпри решении этого кубического уравнения может не дать сходимости. Это следствие вырождения исходной системы (1.2.3), и за этим надо следить (варьируя и т.п.). Например, задается некоторая точность сходимости итерационного процесса и минимально () и максимально () допустимые числа итераций. Если заитераций процесс не сходится, уменьшают, если сходится за меньшее, чем число итераций, то увеличивают и т.д.[25]

Приведем основные идеи метода Розенброка, реализованного в математическом пакете MathCAD [26]. Он основан на приведении жестких обыкновенных дифференциальных уравнений:

к разностной схеме вида

Здесь – шаг интегрирования, — некоторые неизвестные параметры, а

Если рассматривается не одно уравнение, а система уравнений (с неизвестным параметром у), тоявляется матрицей размера , составленной из частных производных (якобианом).

Если осуществить разложения решения в ряд Тейлора в точке , и подставить его в разностную форму, то после несложных преобразований, можно вычислить конкретные значения параметров, которые превращают уравнение в разностной форме в верное равенство. А именно

Таким образом, алгоритм Розенброка основан на следующих действиях, выполняемых на каждом i -м шаге интегрирования:

1. Вычисляется матрица производных в точке .

2. Следующая точка находится из матричного уравнения в разностной форме с коэффициентами .

Исходя из этого, алгоритм метода Розенброка является одношаговым и безытерационным. Однако, как видно из формулы алгоритма, пересчет каждого шага требует, во-первых, численного определения производных функции . Во-вторых, подразумевается решение системы линейных уравнений.

Метод Булирша-Шера — это метод решения жесткой системы обыкновенных дифференциальных уравнений первого порядка с гладкими правыми частями. Гладкость правых частей является необходимой для работы метода. Если правые части системы не являются гладкими или содержат разрывы, то лучше использовать метод Рунге-Кутта. В случае же гладкой системы метод Булирша-Шера позволяет добиться существенно большей точности, чем метод Рунге-Кутта.

Опишем принцип работы метода. Основной идеей метода является вычисление состояния системы в точке , как результата двух шагов длины , четырех шагов длины, восьми шагов длины и так далее с последующей экстраполяцией результатов. Метод строит рациональную интерполирующую функцию, которая в точке проходит через состояние системы после двух таких шагов, в точке проходит через состояние системы после четырех таких шагов, и т.д., а затем вычисляет значение этой функции в точке , проводя экстраполяцию.

Гладкость правых частей приводит к тому, что вычисленное при помощи экстраполяции состояние системы оказывается очень близко к действительному, а использование рациональной экстраполяции вместо полиномиальной позволяет ещё больше повысить точность.

Таким образом проводится один шаг метода, после чего принимается решение — следует ли изменять шаг, а если да — то в какую сторону. При этом используется оценка погрешности, которую мы получаем в качестве дополнительного результата при рациональной экстраполяции. Следует отметить, что алгоритм решает автономную систему, т.е. если уравнения системы содержат время, то необходимо ввести время в качестве переменной, производная от которой тождественно равна единице [27].

При решении жесткой системы дифференциальных уравнений необходимо использовать функции, специально разработанных для решения жестких систем дифференциальных уравнений. Функции S tiffb, S tiffr реализуют соответственно методы Булирша- Шера и Розенброка.

Обращение к функциям выглядит следующим образом:

— у₀ — вектор начальных условий размерности (порядок обыкновенного дифференциального уравнения или число уравнений в системе обыкновенного дифференциального уравнения);

— t₀,t_i –граничные точки интервала, на котором ищется решение системы обыкновенного дифференциального уравнения;

— М — число точек (не считая начальной), в которой ищется решение;

— F — векторная функция F(t,y) размера,содержащая первые производные неизвестных функций;

— J – матричная функция J(t,y) размера, составленная из вектора производных функции F(t,y)) по t (правый столбец) и ее якобиана (левых столбцов).

Рассмотрим примеры решения жесткой системы дифференциальных уравнений методом Розенброка и Булирша-Шера с помощью встроенных функций MathCAD S tiffr (y₀,t₀,t_i,M,F, j) и Stiffr ( y ₀, t ₀, t _i , M , F , j ) соответственно.

Решить нелинейную жесткую систему дифференциальных уравнений методом Розенброка [26]:

Дана жесткая система обыкновенных дифференциальных уравнений[26]

с начальными условиями. Найти решение системы методом Булирша-Шера. Решение найдено с помощью встроенной функции Stiffb .

Найти решение задачи Коши для следующей жесткой системы методом Булирша – Шера и методом Розенброка [26]:

🌟 Видео

4. Однородные дифференциальные уравнения (часть 1)Скачать

Системы дифференциальных уравнений. Часть 2Скачать