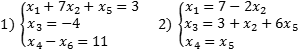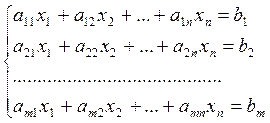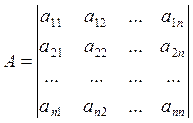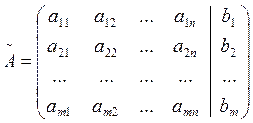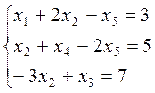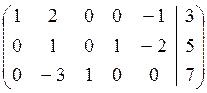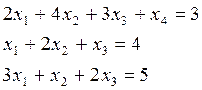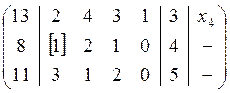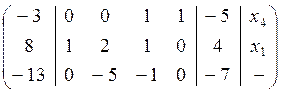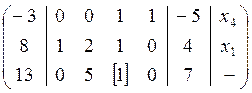Что означает фраза «ранг матрицы равен $r$»? Она означает, что есть хотя бы один минор $r$-го порядка, который не равен нулю. Напомню, что такой минор называется базисным. Базисных миноров может быть несколько. При этом все миноры, порядок которых выше $r$, равны нулю или не существуют.
Выбрать $r$ базисных переменных в общем случае можно различными способами. В примерах я покажу наиболее часто используемый способ выбора.
Во всех изложенных ниже примерах матрицу системы будем обозначать буквой $A$, а расширенную матрицу системы – буквой $widetilde$.
Решить СЛАУ $ left < begin& 3x_1-6x_2+9x_3+13x_4=9\ & -x_1+2x_2+x_3+x_4=-11;\ & x_1-2x_2+2x_3+3x_4=5. end right.$. Если система является неопределённой, указать базисное решение.
Итак, мы имеем СЛАУ, у которой 3 уравнения и 4 переменных: $x_1$, $x_2$, $x_3$, $x_4$. Так как количество переменных больше количества уравнений, то такая система не может иметь единственное решение (чуть позже мы строго докажем это предложение на основе теоремы Кронекера-Капелли). Найдём решения СЛАУ, используя метод Гаусса:
$$ left( begin 3 & -6 & 9 & 13 & 9 \ -1 & 2 & 1 & 1 & -11 \ 1 & -2 & 2 & 3 & 5 end right) rightarrow left|begin & text\ & text\ & text endright| rightarrow \ rightarrowleft( begin 1 & -2 & 2 & 3 & 5\ -1 & 2 & 1 & 1 & -11 \ 3 & -6 & 9 & 13 & 9 end right) begin phantom \ II+I\ III-3cdot Iend rightarrow left( begin 1 & -2 & 2 & 3 & 5\ 0 & 0 & 3 & 4 & -6 \ 0 & 0 & 3 & 4 & -6 endright) begin phantom \ phantom\ III-IIend rightarrow \ rightarrowleft( begin 1 & -2 & 2 & 3 & 5\ 0 & 0 & 3 & 4 & -6 \ 0 & 0 & 0 & 0 & 0 endright) $$
Мы завершили прямой ход метода Гаусса, приведя расширенную матрицу системы к ступенчатому виду. Слева от черты расположены элементы преобразованной матрицы системы, которую мы также привели к ступенчатому виду. Напомню, что если некая матрица приведена к ступенчатому виду, то её ранг равен количеству ненулевых строк.
И матрица системы, и расширенная матрица системы после эквивалентных преобразований приведены к ступенчатому виду; они содержат по две ненулевых строки. Вывод: $rang A=rangwidetilde = 2$.
Итак, заданная СЛАУ содержит 4 переменных (обозначим их количество как $n$, т.е. $n=4$). Кроме того, ранги матрицы системы и расширенной матрицы системы равны между собой и равны числу $r=2$. Так как $r < n$, то согласно следствию из теоремы Кронекера-Капелли СЛАУ является неопределённой (имеет бесконечное количество решений).
Найдём эти решения. Для начала выберем базисные переменные. Их количество должно равняться $r$, т.е. в нашем случае имеем две базисные переменные. Какие именно переменные (ведь у нас их 4 штуки) принять в качестве базисных? Обычно в качестве базисных переменных берут те переменные, которые расположены на первых местах в ненулевых строках преобразованной матрицы системы, т.е. на «ступеньках». Что это за «ступеньки» показано на рисунке:
На «ступеньках» стоят числа из столбцов №1 и №3. Первый столбец соответствует переменной $x_1$, а третий столбец соответствует переменной $x_3$. Именно переменные $x_1$ и $x_3$ примем в качестве базисных.
В принципе, если вас интересует именно методика решения таких систем, то можно пропускать нижеследующее примечание и читать далее. Если вы хотите выяснить, почему можно в качестве базисных взять именно эти переменные, и нельзя ли выбрать иные – прошу раскрыть примечание.
Почему можно принять переменные $x_1$ и $x_3$ в качестве базисных? Для ответа на этот вопрос давайте вспомним, что ранг матрицы системы равен числу $r=2$. Это говорит о том, что все миноры данной матрицы, порядок которых выше 2, либо равны нулю, либо не существуют. Ненулевые миноры есть только среди миноров второго порядка. Выберем какой-либо ненулевой минор второго порядка. Мы можем выбирать его как в исходной матрице системы $A$, т.е. в матрице $left( begin 3 & -6 & 9 & 13 \ -1 & 2 & 1 & 1 \ 1 & -2 & 2 & 3 end right)$, так и в преобразованной матрице системы, т.е. в $left( begin 1 & -2 & 2 & 3 \ 0 & 0 & 3 & 4 \ 0 & 0 & 0 & 0 endright)$. Так как в преобразованной матрице системы побольше нулей, то будем работать именно с нею.
Итак, давайте выберем минор второго порядка, элементы которого находятся на пересечении строк №1 и №2, и столбцов №1 и №2:
$$ M_^=left| begin 1 & -2 \ 0 & 0 endright|=1cdot 0-(-2)cdot 0=0. $$
Вывод: выбранный нами минор второго порядка не является базисным, ибо он равен нулю. Так как элементы этого минора взяты из столбца №1 (он соответствует переменной $x_1$) и столбца №2 (он соответствует переменной $x_2$), то пара переменных $x_1$ и $x_2$ не могут быть базисными переменными.
Осуществим вторую попытку, взяв минор второго порядка, элементы которого лежат на пересечении строк №1, №2 и столбцов №3 и №4:
$$ M_^=left| begin 2 & 3\ 3 & 4 endright|=2cdot 4-3cdot 3=-1. $$
Вывод: выбранный нами минор второго порядка является базисным, ибо он не равен нулю. Так как элементы этого минора взяты из столбца №3 (он соответствует переменной $x_3$) и столбца №4 (он соответствует переменной $x_4$), то пару переменных $x_3$ и $x_4$ можно принять в качестве базисных.
Сделаем и третью попытку, найдя значение минора, элементы которого расположены на пересечении строк №1, №2 и столбцов №1 и №3:
Вывод: выбранный нами минор второго порядка является базисным, ибо он не равен нулю. Так как элементы этого минора взяты из столбца №1 (он соответствует переменной $x_1$) и столбца №3 (он соответствует переменной $x_3$), то пару переменных $x_1$ и $x_3$ можно принять в качестве базисных.
Как видите, выбор базисных переменных не является однозначным. На самом деле количество вариантов выбора не превышает количество размещений из $n$ элементов по $r$, т.е. не больше чем $C_^$.
В рассматриваемом примере в качестве баисных были приняты переменные $x_1$ и $x_3$ – сугубо из соображений удобства дальнейшего решения. В чём это удобство состоит, будет видно чуток позже.
Базисные переменные выбраны: это $x_1$ и $x_3$. Остальные $n-r=2$ переменных (т.е. $x_2$ и $x_4$) являются свободными. Нам нужно выразить базисные переменные через свободные.
Я предпочитаю работать с системой в матричной форме записи. Для начала очистим полученную матрицу $left( begin 1 & -2 & 2 & 3 & 5\ 0 & 0 & 3 & 4 & -6 \ 0 & 0 & 0 & 0 & 0 endright)$ от нулевой строки:
$$ left( begin 1 & -2 & 2 & 3 & 5\ 0 & 0 & 3 & 4 & -6 endright) $$
Свободным переменным, т.е. $x_2$ и $x_4$, соответствуют столбцы №2 и №4. Перенесём эти столбцы за черту. Знак всех элементов переносимых столбцов изменится на противоположный:
Почему меняются знаки? Что вообще значит это перенесение столбцов? показатьскрыть
Давайте обратимся к расширенной матрице системы, которая после преобразований имеет вид $left( begin 1 & -2 & 2 & 3 & 5\ 0 & 0 & 3 & 4 & -6 endright)$. Перейдём от матрицы к уравнениям. Первая строка соответствует уравнению $x_1-2x_2+2x_3+3x_4=5$, а вторая строка соответствует уравнению $3x_3+4x_4=-6$. Теперь перенесём свободные переменные $x_2$ и $x_4$ в правые части уравнений. Естественно, что когда мы переносим выражение $4x_4$ в правую часть уравнения, то знак его изменится на противоположный, и в правой части появится $-4x_4$.
Если опять записать полученную систему в виде матрицы, то мы и получим матрицу с перенесёнными за черту столбцами.
А теперь продолжим решение обычным методом Гаусса. Наша цель: сделать матрицу до черты единичной. Для начала разделим вторую строку на 3, а потом продолжим преобразования обратного хода метода Гаусса:
$$ left( begin 1 & 2 & 5 & 2 & -3\ 0 & 3 & -6 & 0 & -4 endright) begin phantom \ II:3 end rightarrow left( begin 1 & 2 & 5 & 2 & -3\ 0 & 1 & -2 & 0 & -4/3 endright) begin I-2cdot II \ phantom end rightarrow \ rightarrow left(begin 1 & 0 & 9 & 2 & -1/3\ 0 & 1 & -2 & 0 & -4/3 endright). $$
Матрица до черты стала единичной, метод Гаусса завершён. Общее решение найдено, осталось лишь записать его. Если вспомнить, что четвёртый столбец соответствует переменной $x_2$, а пятый столбец – переменной $x_4$, то получим:
Нами получено общее решение заданной СЛАУ. Чтобы найти базисное решение, нужно все свободные переменные приравнять к нулю. Т.е. полагая $x_2=0$ и $x_4=0$, будем иметь:
Решение $x_1=9$, $x_2=0$, $x_3=-2$, $x_4=0$ и является базисным решением данной СЛАУ. В принципе, задавая свободным переменным иные значения, можно получить иные частные решения данной системы. Таких частных решений бесконечное количество. Например, принимая $x_2=-4$ и $x_4=1$, получим такое частное решение: $left <begin& x_1=frac;\ & x_2=-4;\ & x_3=-frac;\ & x_4=1. endright.$. Базисное решение, которые мы нашли ранее – лишь одно из бесконечного множества частных решений заданной СЛАУ.
Если есть желание, то полученное решение можно проверить. Например, подставляя $x_1=9+2x_2-fracx_4$ и $x_3=-2-fracx_4$ в левую часть первого уравнения, получим:
$$ 3x_1-6x_2+9x_3+13x_4=3cdot left(9+2x_2-fracx_4right)-6x_2+9cdot left(-2-fracx_4right)+13x_4=9. $$
Проверка первого уравнения увенчалась успехом; точно так же можно проверить второе и третье уравнения.
Если система является неопределённой, указать базисное решение.
Похожий пример уже был решен в теме «метод Крамера» (пример №4). Переменные $x_4$ и $x_5$ были перенесены в правые части, а дальше применялись стандартные операции метода Крамера. Однако такой метод решения не гарантирует достижения результата. Например, мы переносим некие переменные в правую часть, а оставшийся определитель оказывается равным нулю, – что тогда? Решать перебором? 🙂 Поэтому гораздо удобнее применять преобразования метода Гаусса, как и в предыдущем примере.
$$ left( begin 1 & -2 & 4 & 0 & 2 & 0\ 4 & -11 & 21 & -2 & 3 & -1\ -3 & 5 & -13 & -4 & 1 & -2 end right) begin phantom \ II-4cdot I\ III+3cdot Iend rightarrow left( begin 1 & -2 & 4 & 0 & 2 & 0\ 0 & -3 & 5 & -2 & -5 & -1\ 0 & -1 & -1 & -4 & 7 & -2 end right) rightarrow \ rightarrow left|begin & text\ & text\ & text endright|rightarrow left( begin 1 & -2 & 4 & 0 & 2 & 0\ 0 & -1 & -1 & -4 & 7 & -2\ 0 & -3 & 5 & -2 & -5 & -1 end right) begin phantom \ phantom\ III-3cdot Iend rightarrow \ rightarrow left( begin 1 & -2 & 4 & 0 & 2 & 0\ 0 & -1 & -1 & -4 & 7 & -2\ 0 & 0 & 8 & 10 & -26 & 5 end right). $$
Матрица системы и расширенная матрица системы приведены к трапециевидной форме. Ранги этих матриц равны между собой и равны числу 3, т.е. $rang A=rangwidetilde = 3$. Так как ранги равны между собой и меньше, чем количество переменных, то согласно следствию из теоремы Кронекера-Капелли данная система имеет бесконечное количество решений.
Количество неизвестных $n=5$, ранги обеих матриц $r=3$, поэтому нужно выбрать три базисных переменных и $n-r=2$ свободных переменных. Применяя тот же метод «ступенек», что и в предыдущем примере, выберем в качестве базисных переменных $x_1$, $x_2$, $x_3$, а в качестве свободных переменных – $x_4$ и $x_5$.
Столбцы №4 и №5, которые соответствуют свободным переменным, перенесём за черту. После этого разделим третью строку на 8 и продолжим решение методом Гаусса:
$$ left( begin 1 & -2 & 4 & 0 & 0 & -2\ 0 & -1 & -1 & -2 & 4 & -7\ 0 & 0 & 8 & 5 & -10 & 26 end right) begin phantom \ phantom\ III:8end rightarrow left( begin 1 & -2 & 4 & 0 & 0 & -2\ 0 & -1 & -1 & -2 & 4 & -7\ 0 & 0 & 1 & 5/8 & -5/4 & 13/4 end right) begin I-4cdot III \ II+III\ phantomend rightarrow \ left( begin 1 & -2 & 0 & -5/2 & 5 & -15\ 0 & -1 & 0 & -11/8 & 11/4 & -15/4\ 0 & 0 & 1 & 5/8 & -5/4 & 13/4 end right) begin phantom \ IIcdot (-1)\ phantomend rightarrow left( begin 1 & -2 & 0 & -5/2 & 5 & -15\ 0 & 1 & 0 & 11/8 & -11/4 & 15/4\ 0 & 0 & 1 & 5/8 & -5/4 & 13/4 end right) begin I+2cdot II \ phantom\ phantomend rightarrow\ rightarrowleft( begin 1 & 0 & 0 & 1/4 & -1/2 & -15/2\ 0 & 1 & 0 & 11/8 & -11/4 & 15/4\ 0 & 0 & 1 & 5/8 & -5/4 & 13/4 end right) $$
Продолжение этой темы рассмотрим во второй части, где разберём ещё два примера с нахождением общего решения.
Видео:Линейное уравнение с двумя переменными. 7 класс.Скачать
Системы линейных уравнений: основные понятия
— это объединение из n линейных уравнений, каждое из которых содержит k переменных. Записывается это так:
Многие, впервые сталкиваясь с высшей алгеброй, ошибочно полагают, что число уравнений обязательно должно совпадать с числом переменных. В школьной алгебре так обычно и бывает, однако для высшей алгебры это, вообще говоря, неверно.
— это последовательность чисел ( k 1, k 2, . kn ), которая является решением каждого уравнения системы, т.е. при подстановке в это уравнение вместо переменных x 1, x 2, . xn дает верное числовое равенство.
Соответственно, решить систему уравнений — значит найти множество всех ее решений или доказать, что это множество пусто. Поскольку число уравнений и число неизвестных может не совпадать, возможны три случая:
- Система несовместна, т.е. множество всех решений пусто. Достаточно редкий случай, который легко обнаруживается независимо от того, каким методом решать систему.
- Система совместна и определена, т.е. имеет ровно одно решение. Классический вариант, хорошо известный еще со школьной скамьи.
- Система совместна и не определена, т.е. имеет бесконечно много решений. Это самый жесткий вариант. Недостаточно указать, что «система имеет бесконечное множество решений» — надо описать, как устроено это множество.
Переменная xi называется , если она входит только в одно уравнение системы, причем с коэффициентом 1. Другими словами, в остальных уравнениях коэффициент при переменной xi должен быть равен нулю.
Если в каждом уравнении выбрать по одной разрешенной переменной, получим набор разрешенных переменных для всей системы уравнений. Сама система, записанная в таком виде, тоже будет называться разрешенной. Вообще говоря, одну и ту же исходную систему можно свести к разным разрешенным, однако сейчас нас это не волнует. Вот примеры разрешенных систем:
Обе системы являются разрешенными относительно переменных x 1, x 3 и x 4. Впрочем, с тем же успехом можно утверждать, что вторая система — разрешенная относительно x 1, x 3 и x 5. Достаточно переписать самое последнее уравнение в виде x 5 = x 4.
Теперь рассмотрим более общий случай. Пусть всего у нас k переменных, из которых r являются разрешенными. Тогда возможны два случая:
- Число разрешенных переменных r равно общему числу переменных k : r = k . Получаем систему из k уравнений, в которых r = k разрешенных переменных. Такая система является совместной и определенной, т.к. x 1 = b 1, x 2 = b 2, . xk = bk ;
- Число разрешенных переменных r меньше общего числа переменных k : r k . Остальные ( k − r ) переменных называются свободными — они могут принимать любые значения, из которых легко вычисляются разрешенные переменные.
Так, в приведенных выше системах переменные x 2, x 5, x 6 (для первой системы) и x 2, x 5 (для второй) являются свободными. Случай, когда есть свободные переменные, лучше сформулировать в виде теоремы:
Обратите внимание: это очень важный момент! В зависимости от того, как вы запишете итоговую систему, одна и та же переменная может быть как разрешенной, так и свободной. Большинство репетиторов по высшей математике рекомендуют выписывать переменные в лексикографическом порядке, т.е. по возрастанию индекса. Однако вы совершенно не обязаны следовать этому совету.
Теорема. Если в системе из n уравнений переменные x 1, x 2, . xr — разрешенные, а x r + 1, x r + 2, . x k — свободные, то:
- Если задать значения свободным переменным ( x r + 1 = t r + 1, x r + 2 = t r + 2, . xk = tk ), а затем найти значения x 1, x 2, . xr , получим одно из решений.
- Если в двух решениях значения свободных переменных совпадают, то значения разрешенных переменных тоже совпадают, т.е. решения равны.
В чем смысл этой теоремы? Чтобы получить все решения разрешенной системы уравнений, достаточно выделить свободные переменные. Затем, присваивая свободным переменным разные значения, будем получать готовые решения. Вот и все — таким образом можно получить все решения системы. Других решений не существует.
Вывод: разрешенная система уравнений всегда совместна. Если число уравнений в разрешенной системе равно числу переменных, система будет определенной, если меньше — неопределенной.
И все бы хорошо, но возникает вопрос: как из исходной системы уравнений получить разрешенную? Для этого существует метод Гаусса.
Видео:Линейное уравнение с одной переменной. 6 класс.Скачать
Системы линейных уравнений. Основные понятия. Переменные, входящие в уравнения системы
Страницы работы
Содержание работы
Глава 7 Системы линейных уравнений.
Определение 1:Системой линейных уравнений называется система вида:
Определение 2: Решением системы линейных уравнений называется упорядоченный набор чисел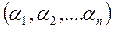 
при подстановке которых в исходную систему каждое из уравнений обращается в тождество.
Определение 3: Основной матрицей системы линейных уравнений называется матрица А размерности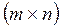 
, образованная из коэффициентов при неизвестных:
Определение 4: Основная матрица А системы дополненная столбцом свободных членов, называется расширенной матрицей системы и обозначается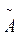 
.
Определение 5: Система уравнений называется совместной, если она имеет хотя бы одно решение и несовместной если у неё нет.
Определение 6: Система уравнений называется однородной, если все свободные члены равны нулю.
Определение 7: Неизвестная хi в системе линейных уравнений называется базисной, если она встречается в единственном уравнении системы и имеет коэффициент равный единице.
Определение 8: Система уравнений имеет базисный вид, то есть приведена к единичному базису, если в каждом уравнении выделена одна базисная переменная.
Приведём системы базисного вида:
Расширенная матрица этой системы:
Нетрудно увидеть, что базисными переменными в приведённом примере являются переменные х1, х3, х4.
Определение 9: Переменные входящие в уравнения системы и не являющиеся базисными называются свободными переменными.
Определение 10: Две системы линейных уравнений называются равносильными, если множества их решений совпадают. Все несовместные системы равносильны.
Перечислим элементарные преобразования систем, приводящие к равносильным системам:
2. Умножение на число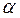 
правой и левой части любого уравнения.
3. Прибавление к левой и правой части i-ого уравнения соответствующих частей j – ого уравнения, умноженных на число .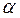
4. Перестановка местами i-ого и j-ого уравнений.
7.2 Решение системы линейных уравнений методом Жордана-Гаусса.
Этот метод позволяет привести к базисному виду совместную систему уравнений.
Элементарные преобразования будем осуществлять по следующей схеме.
1. Выбираем разрешающий элемент в каком либо уравнении и если этот элемент расширенной матрицы не является единицей, то элементы разрешающей строки делим на этот элемент.
2. Разрешающий столбец с помощью элементарных преобразований заполняем нулями.
3. Получаем новую расширенную матрицу, в которой снова выбираем другую разрешающую строку и повторяем все действия.
4. В случае возникновения нулевой строки ее вычеркиваем.
5. В случае возникновения строки вида: 0х1+0х2+0хn=bi система не имеет решений, то есть является несовместной.
Рассмотрим пример решения системы с использованием столбца контрольных сумм КΣ, которые представляют собой суммы всех коэффициентов, соответствующих уравнений. Эти числа преобразуются по тем же правилам, что и остальные элементы матрицы. Контроль состоит в том, что на каждом этапе проверяется совпадение контрольной суммы с суммой всех коэффициентов данного уравнения. Решим систему уравнений.
Составим расширенную матрицу системы, причем в первом столбце будут контрольные суммы, а в последнем будем указывать базисные переменные. Легко видеть что в первом уравнении такой переменной будет переменная х4.
выберем разрешающий элемент во второй строке, пусть это будет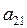 
. Используя элементарные преобразования, получим матрицу у которой все остальные элементы разрешающего столбца были нулевые, для этого выполняются следующие элементарные преобразования:
1. Разрешающая строка умножается на (-2) и складывается с первой строкой, результат записываем на место первой строки.
2. Разрешающая строка умножается на (-3) и складывается с третьей строкой, результат записывается на место третьей строки.
В результате получаем матрицу:
Используя столбец контрольных сумм, сделаем проверку:
Следующим шагом необходимо выбрать разрешающий элемент в третьей строке. В качестве такого элемента можно взять элемент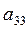 
, но для того чтобы этот элемент стал равным единице, умножим элементы третьей строки на (-1). Получим матрицу вида:
используя элементарные преобразования, преобразуем разрешающий столбец матрицы так, чтобы все элементы кроме разрешающего (базисного) стали равны нулю, для этого выполняем следующие элементарные преобразования.
1. Разрешающая строка умножается на (-1) и складывается со второй строкой, результат записывается на место второй строки.
2. Разрешающая строка умножается на (-1) и суммируется с первой строкой, результат записывается на место первой строки.
💥 Видео
Решение системы линейных уравнений с двумя переменными способом подстановки. 6 класс.Скачать
Урок 7 ЛИНЕЙНОЕ УРАВНЕНИЕ С ОДНОЙ ПЕРЕМЕННОЙСкачать
ЛИНЕЙНОЕ УРАНЕНИЕ С ДВУМЯ ПЕРЕМЕННЫМИ — Как решать линейное уравнение // Алгебра 7 классСкачать
Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать
Линейная зависимость векторовСкачать
ЛИНЕЙНЫЕ УРАВНЕНИЯ - Как решать линейные уравнения // Подготовка к ЕГЭ по МатематикеСкачать
зависимые, независимые и контролируемые переменныеСкачать
Решение системы линейных неравенств с одной переменной. 6 класс.Скачать
Уравнение с двумя переменными и его график. Алгебра, 9 классСкачать
Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать
15. Однородная система линейных уравнений / фундаментальная система решенийСкачать
Линейное уравнение с одной переменной. Практическая часть. 6 класс.Скачать
Что такое зависимая и независимая переменные? Учимся из определять! ЕГЭ по биологииСкачать
Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать
Линейные уравнения с одной переменной, содержащие переменную под знаком модуля. 6 класс.Скачать
Алгебра 7 Линейное уравнение с одной переменнойСкачать
7 класс, 8 урок, Линейное уравнение с двумя переменными и его графикСкачать
Линейное уравнение с одной переменной. Практическая часть. 6 класс.Скачать
